基于有限元分析的橡皮滚筒优化设计

贾振昌

（新乡市新机创新机械有限公司，新乡 453000）

0 引言

胶印机印刷压力与油墨转移率密切相关，是印刷图文良好转移的关键，而滚筒自身精度对印刷压力的精确性和均匀性起着决定性作用。印刷压力过大，引起印刷网点几何增大，光泽度变差，引起实地密度和色密度的变化[1]。胶印机印刷压力值大约为5kgf/cm2～7.5kgf/cm2，橡皮布的压缩量一般为0.1mm。单张纸胶印机的国家标准要求筒身径向跳动在0.02mm以内[2]。

国内印刷机设计的相关专著对印刷滚筒的印刷压力及其对滚筒挠曲变形的影响进行了详尽的研究[3～5]。文献使用三维实体仿真和有限元分析对压印滚筒进行静力分析来提高滚筒的抗弯刚度，对胶印机印刷滚筒在空挡冲击下的弯曲振动和橡皮滚筒不平衡量引起的挠度变化进行研究，对应用三维仿真在滚筒内腔设计加强筋优化滚筒结构的研究，借助有限元分析对滚筒接触过程进行动力学仿真等[6～10]。

但是滚筒缺口和拉紧橡皮布的共同影响引起的筒身弯曲变形对印刷压力均匀性的影响却一直不被人关注，未见到有相关研究报道。单张纸胶印机国家标准也没有对拉紧橡皮布后的筒身径向跳动做出明确要求。对拉紧橡皮布后的橡皮滚筒进行力学分析，应用三维实体仿真和有限元分析对橡皮滚筒进行优化设计以提高滚筒的工作状态刚度，对于提高胶印机的性能品质有着重要意义。

1 橡皮滚筒的力学分析

1.1 橡皮滚筒的结构简介

橡皮滚筒为布置卷橡皮轴而设计成缺口状，橡皮布包裹在滚筒体表面，由卷橡皮轴拉紧橡皮布（如图1所示）。

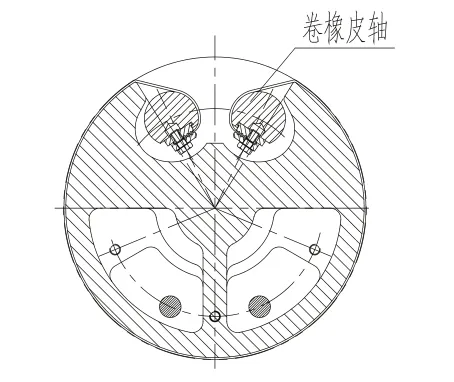
图1 滚筒结构

1.2 拉紧橡皮布后橡皮滚筒的力学分析

精磨加工的橡皮滚筒表面很光滑，橡皮布与滚筒表面间的摩擦力忽略不计。卷紧后橡皮布产生内部张力F，对滚筒表面存在法向力N并产生正压力P。不计摩擦力时橡皮布内的张力F是处处相等的，所以各点的法向力N大小相等。

为确定橡皮布的内部张力F与橡皮布对筒体表面的正压力P之间的关系，取滚筒的水平中心线的下半部分建立数学计算模型（如图3所示）。橡皮布对筒体的法向力N与筒体对橡皮布的支撑力N1是一对作用与反作用力。

图2 数学计算模型

取θ角度上的dθ区域研究，

dθ区域内，法向支撑力的竖直方向的分量为：

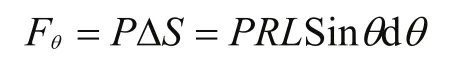
因为Fθ在[0，π]区域内是可叠加的且和与橡皮布张力之和相等，即：ΣFθ= 2F。

把[0 ，π]区域细分成n个dθ区域，当n趋于∞，dθ趋于0，应用定积分的元素法[11]：

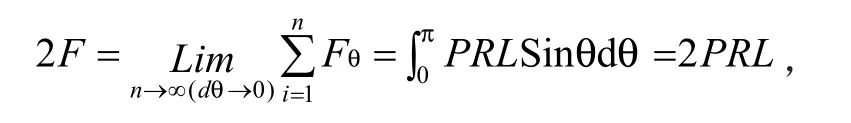
式中各符号的意义如下：

F：橡皮布内部张力（单位N）。

Fθ：dθ区域内滚筒表面对橡皮布的法向支撑力在竖直方向的分量。

N：橡皮布对滚筒表面的法向力（单位N）。

N1：滚筒表面对橡皮布的法向支撑力（单位N）。

R：滚筒筒身半径为0.14m。

L：滚筒筒身长度为1.1m。

P：橡皮布对滚筒表面的正压力（单位N/m2）。

下面计算橡皮布的内部张力F。拉紧橡皮布是依靠给蜗杆施加转矩T1，根据经验测算，转矩T1大约为40 N.m。根据蜗轮蜗杆传动机构的力学计算公式[12]，计算滚筒体表面的正压力P：

式中各符号的意义如下：

：人工施加给蜗杆的转矩40N.m。

：蜗杆的圆周力。

：涡轮的轴向力。

：涡轮的圆周力。

γ：蜗杆分度圆柱上的导程角3°54′。

：蜗杆分度圆直径φ44mm。

：蜗轮分度圆直径φ66mm。

m：蜗轮模数3。

Z：蜗轮齿数22。

D：卷橡皮轴直径φ50mm。

1.3 建立橡皮滚筒的载荷模型

卷橡皮轴受到橡皮布拉力，其作用点在滚筒两端肩铁上的支撑座孔处，其位置距离滚筒轴头很近，引起筒身变形很小，予以忽略不计。只考虑橡皮布对筒身表面的正压力引起的筒身变形。

橡皮滚筒包裹橡皮布后的载荷模型如图3所示。

图3 橡皮滚筒的载荷模型

2 实体仿真和有限元法线性静态分析

对橡皮滚筒进行三维实体仿真，并根据建构的载荷模型进行有限元法线性静态分析，求解筒身的最大位移。并对比卷橡皮布引起的滚筒变形和印刷压力引起的滚筒变形。

2.1 橡皮滚筒的实体仿真

使用SolidWorks PREMIUM三维绘图软件完成实体仿真，如图4所示。

图4 橡皮滚筒的实体仿真

2.2 求解拉紧橡皮布引起载荷作用下橡皮滚筒的位移

2.2.1 有限元模型网格化

SimulationXpress软件中的自动网格器会生成3D四面实体单元网格。

图5 有限元模型网格化

表1 网格信息表

2.2.2 定义材料属性

橡皮滚筒的材质为灰铸铁。

表2 材料属性表

2.2.3 载荷条件与约束

载荷条件：在滚筒筒身表面加载法向正压力P=228571Pa。

约束：在滚筒两端轴头轴承支撑处模拟应用夹具以阻止零件在应用载荷时发生移动。带有夹具的面被视为完整刚性，因此在夹具附近引起不逼真结果。但是这并不影响求解滚筒筒身的位移。

图6 载荷与约束的设定

2.2.4 有限元法线性静态分析求解位移

图7 位移云图

2.3 求解印刷压力作用下橡皮滚筒的位移

根据《印刷机设计》[5]中印刷压力的计算公式求解橡皮滚筒受到的印刷压力：

求接触区宽度b：

求印刷压力FY:

R：滚筒半径150mm。

λ：在印刷压力下橡皮布的压缩量0.1mm。

L：滚筒筒身长度1100mm。

：印刷压力5kgf/cm2。

其他条件不变，仅施加印刷压力的载荷，应用有限元法线性静态分析模拟运行求解位移。

图8 位移云图

2.4 位移云图分析

从图7位移云图知道，拉紧橡皮布引起滚筒筒身中间位置发生最大弯曲变形位移0.16mm。

从图8位移云图知道，印刷压力引起滚筒筒身中间位置发生最大弯曲变形位移0.009mm。

拉紧橡皮布是引起筒身弯曲变形的主要因素。其引起印刷压力的不准确性和不均匀性远远超过胶印机正常印刷所可以接受的数值。

3 橡皮滚筒的结构优化设计与分析

3.1 结构优化设计

橡皮滚筒发生弯曲变形是由于缺口造成应力分布不均。因此考虑在滚筒缺口处增加一根拉轴来平衡橡皮滚筒的内应力。改进后的橡皮滚筒载荷模型如图9所示。

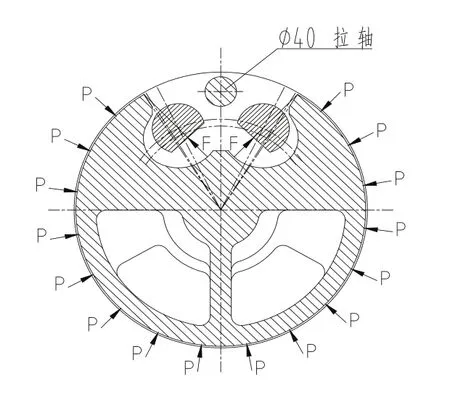
图9 优化设计后橡皮滚筒的载荷模型

3.2 有限元线性静态分析

对优化设计后的橡皮滚筒进行实体仿真并再次有限元法线性静态分析，载荷和约束等条件与卷紧橡皮布状态相同，求解得到如图10所示的移云图。

图10 位移云图

从位移云图知道橡皮滚筒最大弯曲变形位移为0.015mm。优化设计后橡皮滚筒的工作动态刚度得到了很大提高。

4 生产实践验证

我们对研究结果在胶印机生产中进行了实践验证。对优化设计前的橡皮滚筒精度、拉紧橡皮布后的筒身径跳、优化设计后橡皮滚筒在拉紧橡皮布后的筒身径跳、以及印刷压力引起的筒身变形进行了20个色组的数据实测和统计分析。

结果表明：拉紧橡皮布引起筒身变形远大于印刷压力引起的变形。优化设计后的橡皮滚筒的动态刚度提高至0.02mm，满足印刷压力均匀性要求，印刷品的网点、实地密度和色密度等多项印刷性能指标均得到显著改善。

表3 印刷压力测量表

5 结论

1）建立橡皮滚筒的数学计算模型，导出了对橡皮滚筒的筒身正压力P的计算公式。并建立拉紧橡皮布滚筒的载荷模型。

2）通过实体仿真和有限元法分析求解位移云图，拉紧橡皮布引起筒身变形是印刷压力不均匀的主要因素。

3）生产实测数据与有限元分析的结果相一致，验证了研究成果的正确性和实用性。

4）滚筒缺口和拉紧橡皮布的共同影响，引起筒身的弯曲变形这个问题不可忽视。深入研究胶印机印刷滚筒工作状态下的动态刚度，对于提升我国胶印机的性能品质具有非常重要的实际意义。

[1]李晓东,等.胶印机质量控制技术[M].北京:印刷工业出版社,2006:64-91.

[2]全国印刷机械标准化技术委员会.GB/T3264-2010单张纸平版印刷机[S].北京:中国标准出版社,2010.

[3]王淑华,许鑫.印刷机结构与设计[M].北京:印刷工业出版社,1994:5-31.

[4]冯昌伦.胶印机的使用与调节[M].北京:印刷工业出版社,2002.

[5]张海燕.印刷机设计[M].北京:印刷工业出版社,2006.

[6]杨新艳.胶印机压印滚筒的有限元分析[D].西安:西安理工大学,2006.

[7]詹磊.胶印机橡皮滚筒的改进设计及动态特性的研究[D].西安:西安理工大学,2006.

[8]薛凤梅.PZ1650橡皮滚筒动态性能的建模与分析[D].西安:西安理工大学,2008.

[9]刘琳琳,冯载荣,成刚虎.一种印刷滚筒的优化设计方法:中国,200810150917.4[P].2009-02-11.

[10]杨军平.胶印机印刷滚筒间瞬态接触过程动力学分析[D].北京:北京印刷学院,2012.

[11]樊映川.高等数学讲义[M].第2版.北京:高等教育出版社,1964:420-422.

[12]成大先.机械设计手册[M].北京:化学工业出版社.2004:13-295-13-297.