基于近景工业摄影的三维视觉测量
2015-07-07李云雷蒋灵搏
李云雷,蒋灵搏
(1.山东理工大学 机械工程学院,淄博 255091;2.山东工业职业学院 机电工程系,淄博 256414)
0 引言
三维测量技术主要分为接触式和非接触式两种。以三坐标测量机为代表的接触式测量方式,具有很高的测量精度,但通常比较费时且自动化程度低,尤其对大型复杂工件测量时还会受到测量行程的制约。随着光电技术和计算机技术的发展,基于光学原理、以数字图像处理和计算机视觉为主要理论基础的三维视觉测量技术得到飞速发展。三维视觉测量具有非接触、自动化程度高和精度较高等优点,特别适合现代化先进制造业自动化的发展需求[1]。
三维视觉测量包括各种各样的测量方法,如近景工业摄影测量、立体视觉、结构光测量、多目视觉等。其中,近景工业摄影测量特别适合大型复杂工件的三维检测,在反求工程、机械零件检测、虚拟现实等领域应用前景广阔[2]。近景工业摄影测量技术在国外发展较早,并有成熟的商用软件,如美国GSI公司的V-STARS系统,德国GOM公司的TRITOP系统等[3]。国内高校和研究机构主要有武汉大学、西安交通大学、天津大学等,大多停留在理论研究阶段,其中西安交通大学开发了一套近景工业摄影测量系统XJTUDP[4]。
本文在介绍近景工业摄影测量工作原理的基础上,分别研究了三项关键技术:标志点中心坐标的精确定位、基于本质矩阵分解的相对定向和光束法平差解算。精度评定采用大尺寸棋盘格角点之间多组距离的测量来实现。工程实验以粘贴有密集标志点的卫星天线型面为对象,测量出所有标志点的精确三维坐标,同时拟合出型面的三维结构。
1 近景工业摄影测量的关键技术
近景工业摄影测量基于数字图像处理技术和摄影测量技术,将被测物体表面的结构特征转换为高精度的离散三维坐标。其基本工作过程如下:在被测物体表面及周围放置标志点,然后从不同角度和位置拍摄,得到多幅图像。经过数字图像处理、标志点的中心定位,得到标志点几何中心的准确像素坐标。利用这些结果,再经过相对定向、三维重建和光束法平差,最后引入比例棒的比例因子,即可计算出所有标志点精确的三维坐标。
1.1 标志点中心坐标的精确定位
圆形标志点经透镜成像后为椭圆,如果椭圆在像平面占有几个或是十几个像素时,可以近似认为椭圆中心即为标志点中心的像素位置。为实现对椭圆中心的亚像素级精确定位,首先利用Canny边缘检测算子[5]确定椭圆的像素级边缘点,再采用基于灰度加权的质心法,确定标志点的精确中心位置。
质心法是对图像中的圆、椭圆和矩形等中心对称目标进行高精度定位的常用算法。所谓灰度加权质心法,即以像素的灰度值为权,计算标志图像内所有像素坐标的加权平均值,计算公式为:
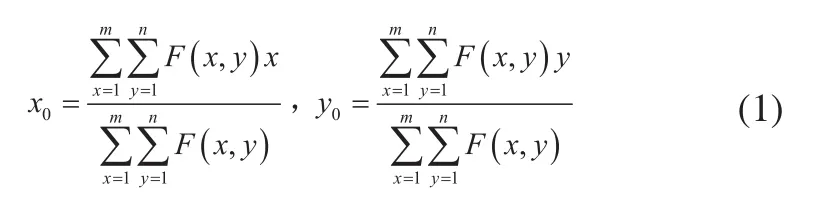
式中,(x0,y0)为标志点中心的像素坐标,F(x,y)为权值,即像素(x,y)的灰度值。标志点中心坐标提取的过程如图1所示。

图1 标志点中心坐标的精确提取
1.2 基于本质矩阵分解的相对定向
相对定向是在立体像对所在的局部坐标系中,确定一张像片相对于另一张像片的旋转矩阵R和平移矢量t[6]。传统的解析摄影测量将代表旋转矩阵的三个旋转角初值设定为零,平移矢量中的首个参数设定为1,后两个参数用小角度表达,这在近似垂直摄影的条件下,通过方程迭代最终可收敛于正确解。但在近景工业摄影中,多数情况是利用“手持”相机的多基线、大倾角摄影,传统方法会出现不收敛的情况。本文采用计算机视觉中本质矩阵分解的方法,可以获得稳定的相对定向参数。
假设平移矢量t=[bx by bz],基于摄影测量学中的共面条件方程[7],可以推导出本质矩阵e和R、t之间的关系:
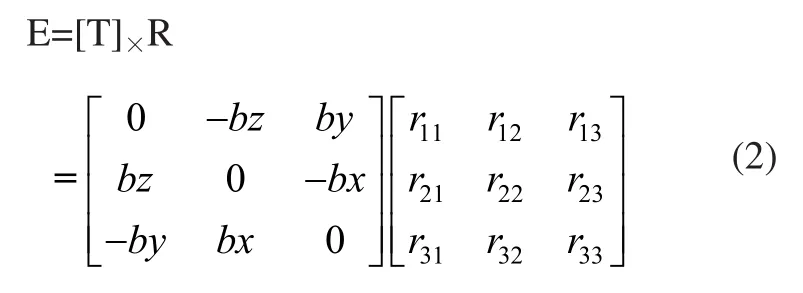
因此,只要计算出本质矩阵E,再对其做适当分解便可获得相对定向参数R和t。本质矩阵的计算方法如下,将其写成矩阵的一般形式:
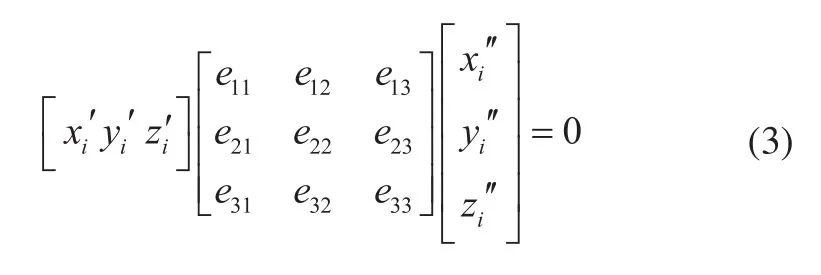
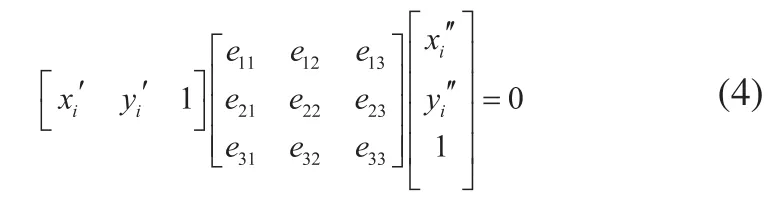
式(4)展开得到关于九个未知参数的方程。一对同名点对应一个方程,n个同名点得到n个方程,得:

A是n×m阶的矩阵,其中m=9。设行向量为ai,则其表达式为:
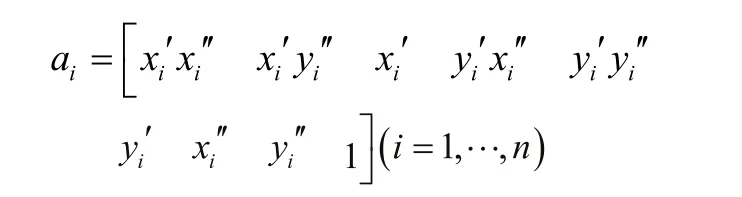
e的表达式为:
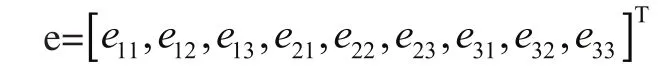
计算中先对A进行奇异值分解(SVD)。奇异值分解表述为:设A是n×m阶复矩阵,则存在n阶酉阵U和m阶酉阵V,使得:

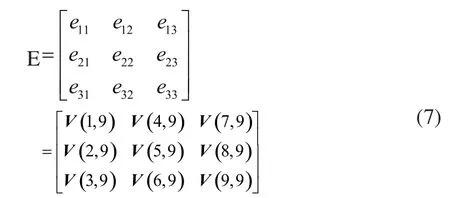
确定了本质矩阵E之后,再对其进行奇异值(SVD)分解:

则旋转矩阵R和平移矢量t的值为:
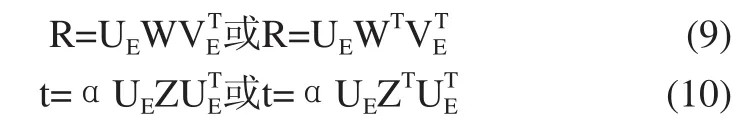
其中,α为不等于零的任意常数。W和Z分别为:

由此可见,这里共有四组解,其中仅有一组是正确的。判断的方法是:任选一对同名点P'i和P''i,根据四组R和t的值,可以计算这对同名点对应的物方点Pi在左、右相机坐标系中的坐标,其中仅有一组的两个坐标点都位于左右相机的前方(即其z坐标同为正),其对应的R和t即为正确解。
1.3 光束法平差解算
光束法平差的数学模型是基于摄影测量共线方程,该方程的表达式为:

方程(12)实质上描述了从世界坐标(X,Y,Z)到对应的图像像素坐标的转换关系。式中是像片的内方位元素,则是像片的外方位元素。外方位元素也可表示为其中是旋转矩阵的三个旋转角。
光束法平差解算是一种把被测点的空间坐标和像素坐标以及所有像片的内方位元素、外方位元素量测数据的一部分或全部视作观测值,以整体地同时求解它们的数值的解算方法,能极大的提高摄影测量的系统精度。光束法平差数学模型的一般表达式为:
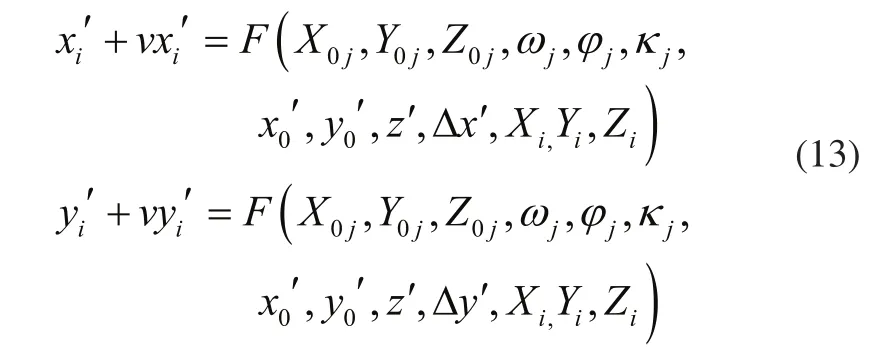
式(13)中,i是点的序号,j是像片的序号。
假设像片的内方位元素已知,以被测点的空间坐标和像片的外方位元素作为观测值。结合式(12)和式(13),可列写出基于共线方程的光束法平差的单点误差方程为:

式(14)列出的是第i个点相对于第j张像片的误差方程,由此可以列写出所有点相对于全部像片的误差方程,联立之后得到光束法平差总的误差方程。引入各观测值的近似值,使用最小二乘法迭代求解,最终可获得各观测值的精确解。
2 精度测试
近景工业摄影测量的精度评测一般参照德国VDI/VDE2634标准[8],受试验条件限制,本文采用图2所示的大尺寸棋盘格作为测试标准。在棋盘格周围及内部放置23个标志点,用于像片间的相对定向,其中框格标记的两个标志点之间的标准距离为2200.140mm,作为比例尺使用。摄站位置围绕棋盘格环形分布,拍摄距离约1.5m,共拍摄12张像片,作为一组。经过相对定向、初步三维重建和光束法平差解算,可以计算出棋盘格每个角点的精确空间坐标。
取图2中的5段距离进行精度评价,并重复拍摄8组,测量结果如表1所示。

图2 采用大尺寸棋盘格的精度测试现场
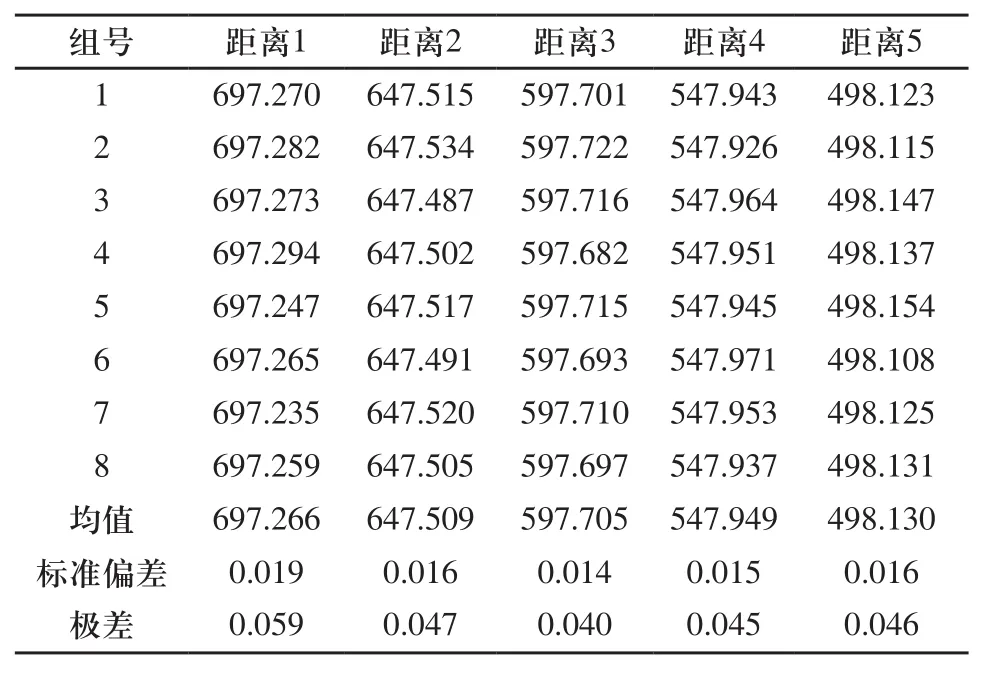
表1 摄影测量的计算结果(mm)
由表1可得,各组的标准偏差均控制在0.02mm以内,极差不超过0.06mm。这充分表明,精度测试试验的三维重建结果重复精度较高,鲁棒性较好,各组的相对误差均优于0.15mm/m。
3 工程测量试验
工程测量试验以口径1.1m的小型卫星天线为测量对象,如图3(a)所示。天线表面粘贴有标志点、编码标志,并放置了比例尺。标志点分5圈布置,共计108个,构成天线表面的形貌。12个编码标志用于摄站间的相对定向,为计算方便,以摄站1处的相机坐标系作为世界坐标系(如图3(b)所示),比例尺用以确定世界坐标系的长度基准。

图3 小型卫星天线表面的摄影测量
手持相机从8个角度围绕天线依次拍摄,每个摄站的位姿如图3(b)所示,每张像片都包含了天线表面的完整图像。相机型号为尼康D3200,等效焦距27mm,摄影距离约1.5m。在拍摄之前,相机已经标定,即每张像片的内方位元素已知。通过其他7个摄站与摄站1的相对定向,确立了所有像片的外方位元素。利用摄站5和摄站1的空间前方交会计算出所有标志点的近似三维坐标。最后将像片的内方位元素、外方位元素和标志点的近似三维坐标进行光束法平差整体解算,得到标志点的精确三维坐标。图4是由所有标志点拟合的天线表面,直观反映出了天线的曲面结构特征。梯度代表了拟合曲面三维坐标中的Z值变化。
4 结论
针对大型复杂工件的三维接触测量中效率及自动化程度低,且易受测量仪器的行程制约等问题,提出了基于近景工业摄影的三维视觉非接触测量方法。该方法在精确提取标志点中心像素坐标的基础上,利用基于本质矩阵分解的相对定向技术可以稳定获得像片的外方位元素,最后借助光束法平差算法精确计算出每个标志点的三维空间坐标。
基于大尺寸棋盘格的精度测试试验表明,该方法的三维重建精度较高,鲁棒性好。针对小型卫星天线的工程测量试验则进一步验证了该方法在实践中的可行性。同时,基于近景工业摄影的三维视觉测量主要借助计算机技术实现图像等相关数据的处理,易于实现自动化,并可根据被测对象的表面形貌灵活布置标志点,测量范围从几米到几十米甚至更大,几乎不受测量对象几何尺寸的影响。
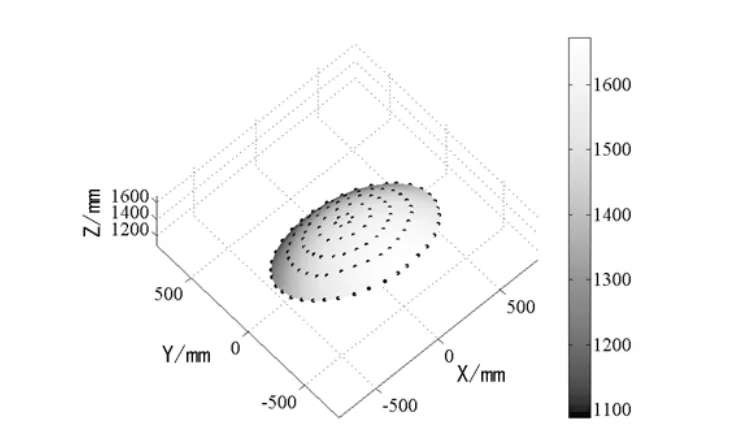
图4 小型卫星天线的拟合曲面(背面方向观测)
[1]孙军华,张广军,魏振忠,等.大型自由曲面移动式三维视觉测量系统[J].仪器仪表学报,2006,27(12):1688-1691.
[2]肖振中.基于工业摄影和机器视觉的三维形貌与变形测量关键技术研究[D].西安:西安交通大学,2010.
[3]El-Hakim S F.Videometrics I, II, III[J].SPIE(SO277-786X),2067,2350:1992-1994.
[4]张德海,梁晋,唐正宗,等.大型复杂曲面产品近景工业摄影测量系统开发[J].光电工程,2009,36(5):122-128.
[5]张广军.机器视觉[M].北京:科学出版社,2005.
[6]LUHMANN T, ROBSON S, KYLE S, HARLEY I.Close Range Photogrammetry:Principles,Techniques and Applications[M].Dunbeath:Whittles Publishing,2006.
[7]张剑清,潘励,王树根.摄影测量学[M].武汉:武汉大学出版社,2003.
[8]Optical 3D measuring systems-Multiple view systems based on area scanning[S].VDI/VDE 2364 Blatt3.2006.German.ICS17.040.01.
