一种适用于高精度视觉测量的边缘检测方法

赵 萍，蔡清华，赵文珍

（1.辽宁省交通高等专科学校，沈阳 110122；2.中航(沈阳)高新科技有限公司，沈阳 110141；3.辽宁科技学院 机械工程学院，本溪 117004）

0 引言

机器视觉测量系统具有非接触、速度快、全视场等突出优点，可实现在线检测、动态检测、实时分析、实时控制等功能，具有高效、高精度、无损伤的检测特点，可以满足现代精密测量技术的发展需要，目前已广泛应用于工业、农业、航空、军事、医学和食品等领域，并得到了极大的关注。但由于系统的复杂性，在测量过程中存在多种随机噪声和系统误差，大多数视觉测量系统的测量精度只达到了0.01mm数量级，只有少数案例在小视场的测量条件下可以达到微米级，因此进一步研究提高视觉测量系统的测量精度仍然是该领域研究的热点[1,2]。

图像在成像、数字化和传输过程中难免会在灰度值上有各种干扰，形成噪声，这些噪声使得图像上像素点的灰度值不能正确地反映空间物体对应点的光强值，由此会造成边缘检测的不确定性，这是实现高精度视觉测量必须解决的问题之一。

为了减小或消除随机噪声对边缘检测的影响，综合利用图像的灰度曲面特性和边缘曲线特性，开发了包括各向异性双边滤波、基于Facet模型的亚像素边缘提取和边缘曲线拟合的三级逼近图像边缘检测算法，提高边缘检测的精度和可靠性。

1 各向异性双边滤波

目前图像滤波方法主要分为线性滤波和非线性滤波两类。线性滤波能够有效地去除高斯噪声，但缺点是在去除噪声的同时，可能会丢失细节处的灰度信息，不具有梯度保持性。非线性滤波可根据边缘特征在不同位置采取不同操作，从而在滤除噪声的同时保持了图像边缘和细节[3]，其中双边滤波由于具有简单、非迭代和局部的特点得到了广泛地应用，但这种滤波方法只能在一定尺度范围内可实现梯度保持性的图像平滑，滤波效果并不理想[4,5]。为此，本文提出了各向异性双边滤波算法（ABF）。

各向异性双边滤波可由式(1)来描述。

式中，Ω为滤波窗口，I(i,j)为输入图像，f(x,y)为输出图像，wr(i,j)为灰度高斯核，ws(i,j)为各向异性高斯核，ka为归一化参数。

其中：

本算法对双边滤波的空域权因子进行了重新定义，通过图像的局部特征控制各向异性高斯核的方向角θ和长短轴比例k，使得滤波器具有以下功能：在图像平滑区域采用相同尺度的滤波，即k=1。在图像的边缘，k≈0，滤波器为近似于边缘切线的线状滤波器。这样，在切向由于考虑了较多的边缘点，使边缘点的灰度分布的标准差较小，最大限度地滤除了噪声，在法向滤波近似为0，最大程度地保留了边缘梯度信息。

LST结构张量[6]描述了图像在大小为O(ρ)的邻域内沿特征方向的平均对比度变化，包含着图像的区域特征信息。特征向量v1是灰度变化最快的方向，v2是灰度变化最小的方向，因此就边缘而言，v1可以看作是边缘法线方向，v2可以看作是边缘切线方向，这样就可以通过结构张量控制方向角θ，使方向角θ始终和边缘方向保持一致。将v2分解水平分量v21和垂直分量v22，则方向角θ计算如下：

LST结构张量v1、v2对应的特征值分别为µ1、µ2，在平滑区域 µ1≈ µ2≈ 0 ，在边缘区域 µ1＞＞ µ2≈ 0 。因此可以用它们来定义长短轴比例k，即：

式中，τ为比例因子调整参数，目的是控制k在µ1= 0 时有意义，本文τ取0.005。

分别用均值滤波、高斯滤波、双边滤波、各向异性双边滤波对图1(a)的量块图像进行滤波，滤波效果如图1(b)、图1(c)、图1(d)、图1(e)所示，滤波前后边缘的灰度分布如图2所示，y=30处梯度方向剖面的灰度分布如图3所示。

图1 滤波效果

图2 用Canny算法提取边缘的灰度分布

图3 y=30处梯度方向的灰度分布

通过对图1、图2、图3的分析，可以看出：均值滤波和高斯滤波很好地平滑了图像，但滤波后边缘模糊了，且灰度分布与原图灰度分布的趋势有较大差异，边缘梯度明显减小，由此可能会造成边缘细节信息的丢失；双边滤波在一定尺度内可以保持边缘的梯度，但边缘带的滤波效果不好；采用各向异性双边滤波后边缘处灰度的分布趋势与原图基本吻合，在边缘的法线方向，除了在黑色区域滤掉少许噪声之外，其他位置与原图像几乎重合。由此可见，各向异性双边滤波在提高切向平滑的基础上不会造成细节特征的丢失，且有效地保留了边缘的梯度信息。因此，各向异性双边滤波算法同时具有图像平滑和梯度保持的功能。

2 基于Facet曲面模型亚像素边缘提取

在数字图像中，轮廓是基于像素网格的，控制点之间的横纵坐标是整数，而实际物体的轮廓控制点的横纵坐标是浮点数，因此像素轮廓很难反映实际轮廓的拓扑信息，为此，从20世纪80年代开始，有不少研究者提出了各种各样有效的亚像素边缘定位算法。根据计算原理，亚像素边缘定位方法主要有曲线拟合法、曲面拟合法、矩法和数字相关法[7]。其中，曲面拟合法相对其他方法对噪声的影响不敏感，具有较高的重复定位精度，但存在的问题是由于对每一个像素都要进行邻域的曲面拟合和亚像素位置的计算，计算量很大，这对实时处理相当不利。为此，本文先用改进的Canny算法[8]进行粗定位，提取单像素精度边缘，然后用以像素边缘为中心的邻域数据集拟合Facet曲面模型，根据单边阶跃边缘的特征在像素边缘内确定亚像素边缘位置，实现边缘的精定位。

2D Facet模型[9]是一个以对称邻域中心为坐标原点的二元三次多项式，由下面的公式表达：

式中，x、y是像元的坐标，k1、k2、…、k10是待定系数。

为了保证算法是位置不变的，先建立一个局部坐标系，其原点建立在粗定位点处，则亚像素边缘点在边缘像素中的位置如图4所示。

图4 亚像素边缘点在边缘像素中的位置

则有：

式中，ρ是亚像素边缘点距离像素中心的距离，α是梯度方向。将式(5)代入式(4)，则有：

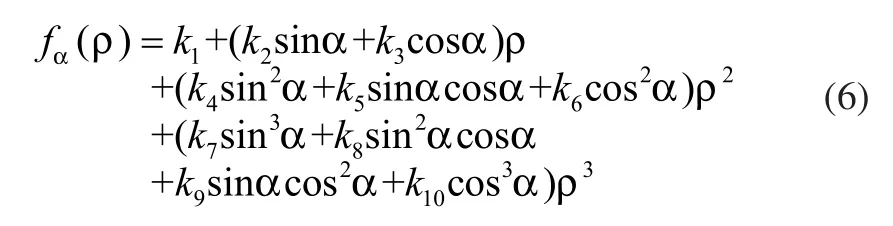
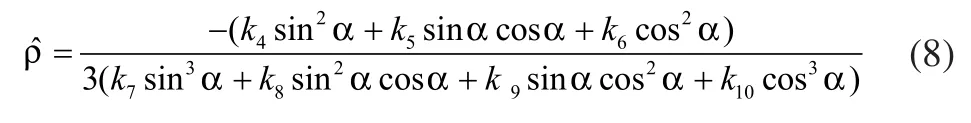
将式(7)、式(8)代入式(9)，就能求得边缘点的亚像素位置。

式中，(x,y)是边缘的亚像素坐标，(xi,yi)是边缘的像素坐标。

2D Facet模型描述了一个二元三次的曲面，为了避免解方程组时出现病态系数矩阵，本文用Chebyshev多项式的张量积来生成正交多项式组作基底来重构式(4)，即：

在邻域S内，用最小二乘法求取拟合系数ci，即：

表明系数ci可通过对图像I(x,y)进行模板运算获得，模板大小为邻域S的范围。与像素(x,y)相对的模板通过式(12)计算：

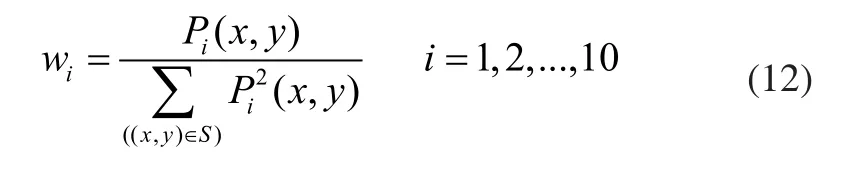
实验表明，5×5窗提取边缘的定位精度最高，且不会产生较大的系统误差，因此，本文采用5×5窗，计算c1～c10的10个模板如图5所示。

使用本文改进算法和传统Facet曲面拟合算法提取如图6所示量块的亚像素边缘如图7(a)所示，边缘点到拟合直线（由经过位置误差补偿后的边缘点拟合）的距离分布如图7(b)所示。

由图7(a)来看，改进算法提取的亚像素边缘更为平滑。从图7(b)来看，改进算法比Facet曲面拟合算法的定位精度略有所提高。从计算效率来看，使用改进算法的程序执行时间是20ms，使用原算法的时间是47ms，速度提高了1.35倍。

图5 5×5卷积模板

图6 量块图像

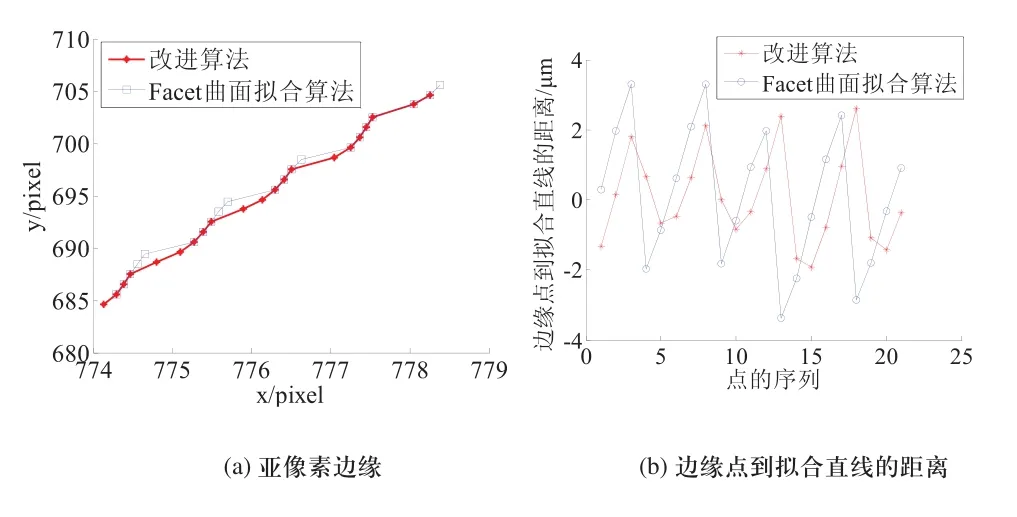
图7 本文改进算法与传统Facet曲面拟合算法的对比

3 亚像素边缘的分段拟合

虽然在前面的环节中，本文将抑制噪声作为选择滤波算法和边缘提取算法的主要准则，但仍然存在一些噪声不能滤除，此外，Facet曲面的拟合和亚像素边缘定位不可避免地引入计算误差，使得亚像素边缘的变化幅度较大，不能满足精密测量的要求。因此为了进一步降低随机噪声和计算误差对边缘定位精度的影响，本文对提取的亚像素边缘点进行最小二乘曲线拟合，通过反算得到抑制掉噪声的新数据。

对于具有显著局部特征的任意曲线的亚像素边缘，使用一个拟合曲线来描述，拟合精度较低，一个好的解决方法是采用分段多项式拟合，在每段区间上进行局部最小二乘拟合。然而，拟合函数在区间分段点上不一定连续，在相邻区间边界附近的拟合效果不理想。为此，本文对每个分段区间的最小二乘系数进行连续性约束的修正，保证拟合函数在每个分段点处的连续性。

将数据(xi,yi)分为k个数据集2, …, k。如果设定每个数据集中包含m个数据，待定系数的个数为n+1，则有：

令：

对上式建立拉格朗日函数，有：

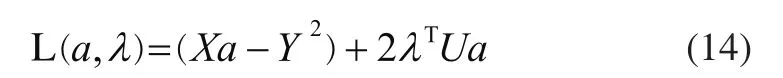
对L(a,λ)求偏导，可解得：

根据式（15）即可求得进行了连续性约束修正的最小二乘回归系数。

4 实验

为验证本文算法的有效性，本文采用piA2400-17gc CCD相机（分辨率为500万（2448×2050）像素，靶面尺寸2/3"（W=8.8mm，H=6.6mm），芯 片 为 Sony ICX625）、日本 Computar镜头M5018-MP2（规格为2/3"，和传感器相配。焦距50mm，光圈1.8-16C，水平视角10.5°）和OPT-FLP平行背光源搭建了视觉测量系统。

在测量条件不变的情况下，使用搭建的视觉测量系统对5mm、8mm量块分别连续采集5张图像，采用本文算法在5张图像上提取相同测量面边缘，以第一张图像的边缘为计算基准，分别计算另外4张图像上的边缘点到基准的距离，重复性定位误差就等于其中最大值。实验结果如表1所示。

表1 定位精度实验结果（单位：像素）

从表1来看，最大重复性定位误差为0.03345像素，由此可以证明本文算法的重复定位精度优于0.1像素。

为了验证本文算法的测量精度，对测量系统标定后，多次测量量块的尺寸，本文选取不同位姿5mm和8mm量块（如图8所示）进行分析，测量结果如表2所示。

图8 测试量块图像

从测量结果来看，采用本文边缘检测算法，所搭建的视觉测量系统的测量精度可以达到±5μm。

5 结论

机器视觉系统应用广泛，但是由于随机误差的影响，影响了系统测量的精确度。本文利用图像的灰度曲面特性和边缘曲线特性，开发了包括各向异性双边滤波、基于Facet模型的亚像素边缘提取和边缘曲线拟合的三级逼近图像边缘检测算法，消除了随机误差的影响，提高了边缘提取的重复定位精度。通过多次对量块边缘的测量，证明该算法的重复定位精度优于0.1像素，使用该算法构建的视觉测量系统测量精度可以达到微米级。因此，该算法能够满足高精度视觉测量系统的使用要求。

表2 量块测量结果（单位：mm）

[1]张少军,苟中魁,李庆利,等.利用数字图像处理技术测量直齿圆柱齿轮几何尺寸[J].光学精密工程,2004,12(6):619-625.

[2]孙秋成.基于机器视觉的轴径测量[D].吉林:吉林工业大学,2010.

[3]王丹.基于各向异性高斯滤波的图像边缘检测方法[D].西安:西安电子科技大学,2010.

[4]张志强,王万玉.一种改进的双边滤波算法[J].中国图形图象学报.2009,14(3):443-447.

[5]王玉灵.基于双边滤波的图像处理算法研究[D].西安:西安电子科技大学,2010.

[6]Weickert J.A scheme for coherence-enhancing diffusion filtering with optimized rotation invariance[J].Journal of Visual Communication and Image Representation, 2002,13(1/2):103-118.

[7]于起峰,尚洋.摄像测量学原理与应用研究[M].北京:科学出版社,2009.

[8]赵萍,赵文珍,段振云,等.一种用于精密样板检测的边缘提取算法.机械设计与制造[J],2012,(12):177-179.

[9]Harlick R M.Digital step edges from zero crossing of second directional derivatives[C].IEEE Transactions on Pattern Analysis and Machine Intelligence.Piscataway, USA: IEEE Press,1984:58-68.