基于欧拉回路的数控火焰切割路径优化研究与实现

陈艳平，李 红，储正阳

（合肥学院 网络与智能信息处理重点实验室，合肥 230601）

0 引言

由于火焰切割设备生产投入小，加工厚度大，因此在适合精度要求不高的粗加工行业得到了广泛的应用。对于数控火焰切割设备来说，切割前必须预先对排样后的零件切割路径进行规划，确定引入引出线的长度和位置，并生成切割控制程序。切割路径的规划对提高设备的生产效率起着举足轻重的作用。现有的绝大多数路径规划软件，都采取切割完一个零件后再切割下一个零件的方法进行路径规划，旨在解决零件的切割顺序上做文章，提出了一些优化算法，如基于零件外轮廓形心的蚁群算法[1,4]，改进的普利姆(Prim) 算法[2,3]等。这些方法在一定程度上缩短了割嘴空程时间，但不能降低点火、熄火次数，而对于火焰切割来说，点火、熄火时间长（80秒左右），严重影响了切割效率。

欧拉图(Euler graph)是图论中一种重要的图。欧拉回路是通过图（有向图或者无向图）中所有边一次且仅一次行遍所有顶点的回路称为欧拉回路。具有欧拉回路的图称为欧拉图。它最早源于1736年瑞士数学家欧拉（Euler）发表的论文“哥尼斯堡七桥问题”，并在各行各业中得到了广泛的应用[6]。因此在零件外轮廓切割问题上提出了一种基于欧拉回路的切割路径规划算法，为切割路径优化问题提供一个新的思路。先计算零件外轮廓的最短距离，然后通过搭桥法构造欧拉图，最后求解该欧拉图的欧拉回路，从而确定整个样板的切割路径。

1 火焰切割问题描述

如图1所示，某一尺寸为L×S的板材上是通过排样程序计算输出的排样图，排样图上紧凑的排列着多个不规则的图形，数控切割任务是将所有图形沿轮廓从板材上切割下来。显然切割得方式有多种，不同的切割路径不同，行程也将不同。

图1 排样后的零件排列图

在文献[1]中利用Prim算法产生最小代价树，生成切割顺序表，按照顺序逐个完成各零件的切割，这种方法在激光或刀片切割时可取，但不适合用于火焰切割。由于火焰切割时不但点火熄火时间长，而且需要在点火熄火位置打孔、设置引入引出线，大大增加了问题求解的难度，降低了切割效率。在充分考虑火焰切割特点的基础上，提出火焰切割的目标是如何规划切割路径，在点火次数尽量少的条件下，求解切割轨迹长度最小值，其中切割轨迹为每个零件的轮廓轨迹与空行程轨迹总和。根据热加工的特点，还必须保证每个零件的轮廓轨迹只切割一次。

2 基于欧拉回路的求解框架

火焰切割中减少点火次数是路径优化中首要问题。尽量减少点火次数的问题与“一笔画问题”非常相似。所谓“一笔画问题”就是画一个图形，在笔不离纸，每条边只画一次而不许重复的情况下，画完该图。“一笔画问题”的本质是一个无向图是否存在欧拉回路的问题。如果该图为欧拉图，则一定能够用一笔画完，并且笔又回到出发点。因此火焰切割问题可以转化为在现有的排样图的基础上构造欧拉图、求解欧拉图的一个欧拉回路。求解思路如图2所示。

图2 路径优化算法流程图

2.1 构建连通图

已知板上有n个多边形形状，记集合为C= G(1)∪G(2)∪, …, ∪G(n)，G(i)为第i个多边形。在图论中，用顶点和边的集合来表示一个图形，故多边形可描述为G(i)=(V，E)，其中V(G(i)) ={vi1,vi2, …, vin}称为图G(i)的顶点集； E(G(i))= {ei1，ei2，…，ein}称为图G(i)的边集合。其中E中的每一个元素ei_i =(vi_j,vi_k)表示连接G(i)图形中vi_j和vi_k节点的无向边。

构建连通图的核心是将相邻形状用辅助连接线连接起来，构成一幅连通图，保证C中任意两个多边形G(i)之间都有通路可达。在切割问题中，添加辅助线时必须满足两点：1）该辅助线不能穿越任何形状；2）尽量保证所有的辅助线长度之和最短。构建连通图问题可以用图论语言这样描述，首先将每个多边形抽象为一个节点，将辅助线抽象为边，边的权值为两点间的欧式距离，那么通过添加辅助线一定能将多边形集合转化为完全连通图。为满足辅助线添加的两个要求，则需要将该完全连通图转化为具有最小权值的生成树。因此构建连通图等价于求取该完全连通图的最小生成树。Prim算法是求解最小生成树的经典算法，改进后的算法描述如下：

Step0：初始化已处理形状列表solved_list为空，未处理形状列表unsolved_list为C。将unsolved_list的第一个形状G(1)加到solved_list中。

Step1：通过改进旋转卡壳算法从unsolved_list中搜索与solved_list中最近的形状G(i)，在距离最近的位置用连接线连接，记录连接点对，添加边ei_i（vi_x，vj_y），将G(i)从unsolved_list中删除，加入到solved_list。

Step2：unsolved_list不为空，则重复Step2；为空，则转向step4。

Step3：算法结束。

通过该算法，生成的连通图如图3所示。

2.2 构建欧拉图

定理1：一个无向连通图是欧拉图的充分必要条件是每个节点的度为偶数[6]。

定理2：一个无向连通图中奇度节点的个数为偶数[6]。

根据定理1、2，对于给定的连通图，若该图中含有2K个奇度点，构建欧拉图问题归结为找到该图中2K个奇度点，求出符合K条欧拉通路间空行程最短的K条添加边[5]。这是最小权最大匹配问题。在火焰切割问题求解中，要求每个零件的轮廓轨迹只切割一次，故添加边只能是连接辅助线。因此根据先验知识，首先在C中找到每个度为奇数的点，给这些点关联的连接辅助线添加平行边得C～，C～一定为欧拉图，如图4所示。

2.3 求欧拉图的一条欧拉回路

Fleury算法是求解欧拉图的欧拉回路的经典算法。使用Fleury算法求欧拉通路（回路）时，每次走一条边，在可能的情况下不走桥。借鉴Fleury算法思路，在求解上述构造的欧拉图中，每次逆时针走一条边，遇到与连接辅助线关联的节点v则走连接辅助线，简单的说就是“先走桥后走边”，从而生成一条能够遍历且只遍历所有的轮廓一次的通路。求解欧拉通路算法描述如下：

图3 构造连通图C

图4 构造欧拉图C

Step1：取离初始位置最近的点v0∈V(C～)，令P0=v0。

Step2：从P0出发，遍历所在多边形G(i)。

Step3：当遇到连接点vi_x，则选择连接线，到达下一个多边形G(i+1)的连接点vi+1_y。

Step4：逆时针遍历与vi+1_y相关联的G(i+1)的边ei+1_z。

Step5：逆时针遍历，遇到连接点，转向Step3。

Step6：当所有的非连接线的边都遍历后（回到起点位置），算法停止。

3 实验结果与分析

将该算法应用到数控火焰切割机床进行实验，输入数据为排样图1，共108个图形。在处理外轮廓切割问题上，该算法只需点火一次，与排样图中形状数量无关。总行程长度由形状的轮廓长度和空行程长度组成，其中空行程长度为连接线长度之和的两倍。性能上优于市场中多种数控切割产品。

本算法与文献[1]中基于零件外轮廓形心的蚁群算法对比数据如表1所示。

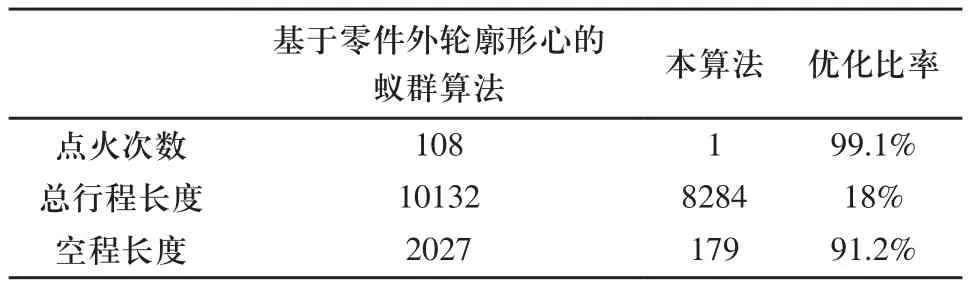
表1 排样图1的切割实验比较

本算法与文献[2]中基于改进的普利姆算法对比数据如表2所示。

本算法与市场占有率较高的瑞丽软件对比数据如表3所示。

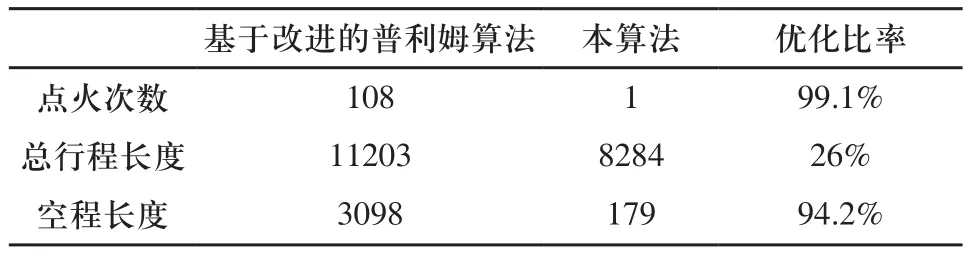
表2 排样图1的切割实验比较

表3 排样图1的切割实验比较

从切割质量上看，本算法为了保证一笔切完，某些形状是分两次，有些甚至是三次切割。对于一个形状而言，由于板材热加工变形收缩，以及机器臂的漂移等因素影响，导致加工后的部件连接点位置出现部分毛刺。对于精细加工工艺而言，可以结合其他补偿方法加以解决。

4 结论

本文研究了基于欧拉回路的外轮廓数控火焰切割路径优化算法。先通过计算外轮廓的距离，充分利用板材空白废料区给近邻的外轮廓添加辅助桥接线（俗称搭桥），构建欧拉图，并在先验知识的指导下，求出一条欧拉回路，从而得到了各零件外轮廓的切割路径。通过在复杂排样条件下的比较测试，本文提出的方法在外轮廓切割上能够保证一笔切割，空程比例也明显降低，生产效率得到极大的提高。它不但能很好地解决了数控火焰切割的路径优化问题，在激光切割，刀片切割等应用领域也能够大大缩短空行程长度。

[1] 朱灯林,陈俊伟,俞洁,董世昌.基于零件形心的数控火焰切割路径的规划[J].机械设计与制造.2006(09):88-90.

[2] 陈飒,施展.板金加工数控切割路径的优化计算[J].上海理工大学学报.2003.25(4):376-378.

[3] 刘会霞,王霄,蔡兰.钣金件数控激光切割割嘴路径的优化[J].计算机辅助设计与图形学学报.2004.16(1):660-665.

[4] 孙鑫.二维激光切割路径优化研究[M].2012.

[5] 刘会霞,王霄,周明,蔡兰.共边排样件激光切割路径的规划[J].中国激光,2004.31(10):1269-1274.

[6] 卜月华.图论及其应用[M].南京:东南大学出版社,2002.