GNSS RTK建立等级控制点精度分析

施 克,雷海林,陈永生,谢尚威

(1.中国能源建设集团辽宁电力勘测设计院有限公司,沈阳 110179;2.东北大学资源与土木工程学院,沈阳 110819)

GNSS RTK建立等级控制点精度分析

施 克1,雷海林2*,陈永生2,谢尚威2

(1.中国能源建设集团辽宁电力勘测设计院有限公司,沈阳 110179;2.东北大学资源与土木工程学院,沈阳 110819)

针对单基站GNSS RTK技术应用广泛,但对其精度探讨不足的问题,选择带状区域用0.5″高精度的全站仪施测高精度控制网,建立实验场地;然后以基准站至流动站间的距离为可控变量,在带状控制网的一端设置GNSS RTK的基准站,在距基准站不同距离的位置上设置流动站,用RTK静态方式采集实时动态数据。利用大量的实验数据得出动态点相对于静态基准站间的相对精度,并以此建立两者之间的点图;根据点图建立两者之间的函数关系,通过反复建模比较确认两者之间成指数函数关系。最后,利用指数函数曲线回归的方法求出了两者之间的关系式,通过数据分析,证明了利用GNSS RTK技术建立等级控制点的可行性。

GNSS RTK;相对精度;曲线回归;等级控制

0 引言

单基站全球卫星导航系统(global navigation satellite system,GNSS)实时动态差分法(realtime kinematic,RTK)技术目前已广泛应用于几乎所有地表的各类高精度定位中,随着GNSS定位技术的发展,GNSS不仅广泛应用于静态定位,而且更广泛地应用于实时高精度动态定位,目前地表90%的导航定位数据采集基本来自GNSS技术[1-5]。GNSS RTK定位主要采用载波相位差分的方法,一般可达到(1 cm+1×10-6×D)的精度,因此被广泛应用于测绘领域。但在实际应用中发现,其标称精度与实际精度存在一定的差距,因此,有必要探讨单基站GNSS RTK的实际精度,使其不仅仅应用于碎部测量等精度要求较低的等外控制测量方面[6]。GNSS RTK技术具有快速定位的优点,若能将其用于更高等级点的建立将可节省大量的人力、物力及财力。

本文主要研究在道路勘测过程中利用GNSS RTK技术建立等级控制点的可行性及其规律性。根据流动站至基准站间距离与动态测量点的精度间的关系及现场的环境总结出一定的规律性。

1 GNSS RTK测定的动态相邻点间的相对误差的分析

首先我们在鞍山市和海城市之间G202国道上选择了一段约20 km长的线路,实验区所跨经纬度范围为:122°54′7.2″E～122°42′39.6″E,41°6′36″N～40°53′27.6″N。随机用高精度全站仪(测角精度为0.5″,测距精度为(1 mm+1×10-6×D))建立了基础控制网,并以该基础控制网的结果作为已知数据,然后利用GNSS RTK技术,在该实验场一端的基础控制网的已知点上建立基准站,流动接收机分别在其他基础控制网已知点上分别设站, 以GNSS RTK模式测出的点的坐标反算出相邻点之间的水平距离S1,然后将各段距离S1与全站仪测出的基础控制网的距离S2作差,即得差值ΔS= │S1-S2│,再求出ΔS/S2的比值。根据此比值即可判断GNSS RTK测定的点的相对精度,再根据现场的环境因素总结出GNSS RTK测量的误差主要来源及其对GNSS RTK定位精度影响的变化规律。

2 点精度与距离之间的误差方程

现以流动站至基准站的距离为x轴,以动态测量获得的点之间的相对误差为y轴,在AutoCAD中绘制点图,如图1所示。从该图中点的分布来看,点的精度与距离之间并不呈线性关系,而是类似指数函数的(y=aebx,y为相对误差,x为流动站至基准站之间的距离)曲线形状

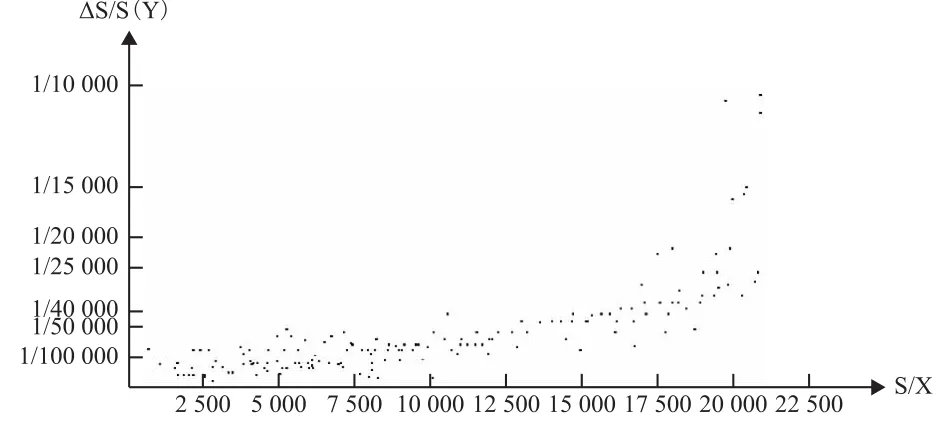
图1 点位精度散点图

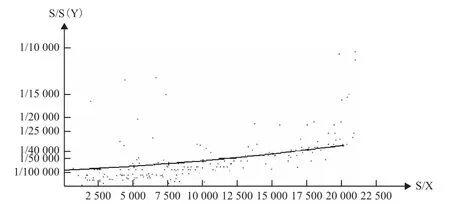
图2 指数函数曲线回归图

从图2可以看出曲线与散点之间吻合的并不好,原因是在7 500 m以内有多个奇异点,其精度较低,是因为在对其进行动态测量时周围环境较差或所测边较短造成的。

显然,式(3)是在测量值含有粗差的情况下求得的,如果用它去指导实践是不合理的,也是不准确的。

现将以上所列的各点去掉后重新回归,求出回归方程为

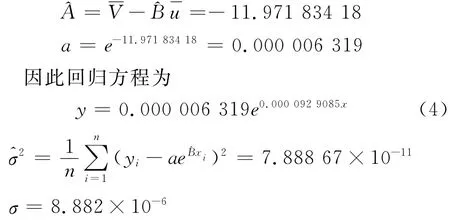
从图3可以看出,该曲线与点图之间吻合较好,在表1中列出了建立四等控制点的满足率及其适应的条件。

图3 去粗差后指数函数曲线回归图

表1 四等控制点满足率与适用条件表

从表1可以看出,在去掉粗差点的情况下,在15 000 m以内用GNSS RTK测量四等点的满足率为100%,在17 500 m以内时,满足率也能达到95%以上,这说明用GNSS RTK测量四等点在一定范围内是完全可以的。在20 km以内用GNSS RTK测量5 s点也是完全可行的。从图3可以看出,如果将(2.4)式的右侧加上8.831E-6,即将曲线向上平移该距离,如图4所示(其中的B线),则该曲线在19 000 m以内在所有的散点之上,曲线方程也就变成(图4中的B线)

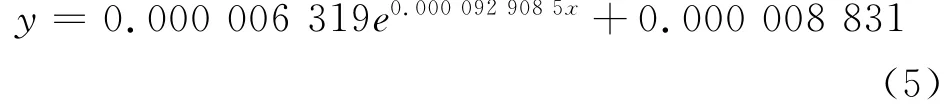
根据式(5)即可预计流动站距基准站不同距离的动态点间的相对精度。当然,此公式只是根据以上实验数据得出的,其结果缺乏理论性。但根据误差理论,若取二倍的相对误差的中误差作为限差,即可将式(4)的右侧加上2σ,则式(4)变为

根据式(6)可预计流动站距基准站不同距离的动态点间的相对精度,依据误差理论的有关知识可知,动态点间的相对精度超过其预计值的概率仅为4.6%,为小概率事件。因此,可以说利用式(6)预计流动站距基准站不同距离的动态点间的相对精度是完全可以的,而且是有理论根据的。将该曲线绘制成图,如图4所示(其中的C线)。

图4 加平移后指数函数回归图

下面根据(6)式对不同等级控制点的精度预计流动站距基准站间最大距离及满足率,可见表2所示。

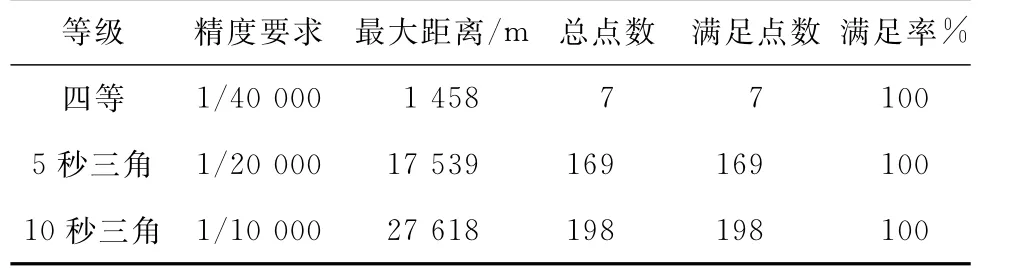
表2 各等级控制点预计满足率与适用条件表

从上表可以看出,根据实验数据对式(6)的验证说明,用式(6)去指导实际测量工作是可行的。但式(6)的应用价值并不大,对应四等点的距离太小。其原因很明显是因为该曲线的方差σ2较大引起的。而σ2较大又是因为流动站至基准站的距离S>16 000 m时的动态点的误差较大所造成的,因此可对S< 16 000 m的各点进行重新回归,求出回归方程为

根据式(8)计算出的不同等级的控制点在流动站距基准站的最大距离及其相应的满足率可见表3。

表3 各等级控制点满足率与适用条件表

从上表可以看出,根据实验数据对(7)式的验证说明了利用(7)式来预计不同精度所对应的最大距离是正确的,相反也可以对不同的距离求出其相应的精度。(7)式的正确性不仅通过实验数据得以证明,而且也有理论根据[7-11],因此用(7)式去指导实际测量工作是可行的。

3 方程的假设检验

3.1 对方程μ=A+Bν的检验

所以方程的两个系数A,B对V都有显著的影响。

4 结束语

1)利用GNSS RTK技术建立等级控制点,控制点的精度与流动站至基准站之间的距离及环境因素有关,其随距离的增长而降低,其变化规律与指数函数的形状相近。当距离超过20 km时,精度陡然下降,在该类型地区建立等级控制点已不可能。

2)根据实验数据得出了利用GNSS RTK技术在建立等级控制点时,由点的精度与基准站至流动站之间距离关系的经验公式计算出当流动站距基准站不超过8 700 m时可建立四等点;当流动站距基准站不超过17 500 m时可建立5″点;当流动站距基准站不超过27 200 m时可建立10″点。但因该公式是利用S小于16 000 m的数据得出的,因此S的最大值应为16 000 m。

3)本项目实验区是在北纬41度左右完成的,由于不同纬度地区受电离层的影响差别会很大,所以不同纬度地区的实验结果会有较大的区别,该结果也只能代表在中国这个纬度区域内的RTK数据采集的精度规律,其他纬度区的实验结果肯定会有区别,这点在实际工程应用中要充分考虑。

[1] PAZIEWSKI J,WIELGOSZ P.Assessment of GPS plus Galileo and multi-frequency Galileo single-epoch precise positioning with network corrections[J].GPS Solutions,2014,18(4):571-9.

[2] TEUNISSEN P J G,ODOLINSKI R,ODIJK D.Instantaneous BeiDou plus GPS RTK positioning with high cut-off elevation angles[J].Journal of Geodesy,2014,88(4):335-50.

[3] ZHANG B C,TEUNISSEN P J G,ODIJK D.A Novel un-differenced-RTK concept[J].Journal of Navigation,2011,64 (S1):80-S91.

[4] 董治方.GNSS RTK技术在农村集体土地所有权调查中的运用与精度分析[J].测绘与空间地理信息,2014,37(5):137-9.

[5] 熊春宝,田力耘,叶作安,等.GNSS RTK技术下超高层结构的动态变形监测[J].测绘通报,2015(7):14-17,31.

[6] 陈永林,柳永全,李辉,等.施工控制与碎部测量同步实施方案及其应用[J].测绘通报,2015(8):82-86.

[7] 吕永江.地籍控制测量[J].测绘通报,1996(2):41-43,38.

[8] 王毅,王玉柱,王红夺.GPS-RTK技术替代传统导线测量精度分析[J].矿山测量,2010(3):57-60,4.

[9] 王勇,吴俐民.网络RTK技术在城市控制测量中的试验与研究[J].城市勘测,2006(4):27-28,32.

[10]许可.像控点代替导线点做RTK点校正的精度分析[J].测绘地理信息,2013,38(5):19-20,4.

[11]邹进贵,童魁,朱勇超.GPS控制测量和精密导线在隧道定向中的应用[J].测绘地理信息,2014,39(2):42-44.

GNSS RTK Accuracy Analysis of Establishing Grade Point

SHI Ke1,LEI Hailin2,CHEN Yongsheng2,XIE Shangwei2
(1.China Energy Engineering Group Co.,Ltd,Liaoning Electric Power Survey and Design Institute, Shenyang 110179,China; 2.Northeastern University,College of Resources and Civil Engineering,Shenyang 110179,China)

GNSS RTK technology has been widely used for single base station,but its accuracy is inadequately discussed.This paper selects the strip area with 0.5 seconds precision Total Station surveying high-precision control network,establishes experimental site;then,with the distance between reference station and rover as controllable variables,it sets GNSS RTK base station at the end of the ribbon control network,in different distance from the reference station position setting rover,the real-time dynamic data acquisition by RTK static mode of operation.A large number of experimental data summarizes the relative accuracy between dynamic point and the static base station,builds the point diagram between them,according to the point diagram to establish the function relationship between them.By comparing modeling repeatedly confirmed a exponential function relationship between the two,using the exponential function curve regression method to calculate the relationship between them, analyzing the collected data,this paper proves the feasibility of using GNSS RTK technology to establish grade control points.

GNSS RTK;curvilinear regression;relative precision;grade control

TN96

A

2095-4999(2015)-04-0106-04

2014-10-18

施克(1966—),男,辽宁彰武人,高级工程师,主要研究方向为卫星定位在电力勘测设计中的应用。

雷海林(1989—),男,湖南邵阳人,工程硕士,研究方向为GNSS数据处理及理论。

施克,雷海林,陈永生,等.GNSS RTK建立等级控制点精度分析[J].导航定位学报,2015,3(4):106-109.SHI Ke,LEI Hailin,CHEN Yongsheng,et al.GNSS RTK Accuracy Analysis of Establishing Grade Point[J].Journal of Navigation and Positioning,2015,3(4):106-109.

10.16547/j.cnki.10-1096.20150421