电磁感应中电路消耗的电功率与安培力做功功率的关系

王忠明

摘 要：利用“两根导体棒以不同的速度做切割磁感线运动”“导体棒在运动磁场中做切割磁感线运动”“回路中动生电动势和感生电动势共存”三种情形来说明“在高中阶段，当磁场不随时间变化时，导体棒中动生电动势对应的电功率与其所受的安培力的做功功率的绝对值相等”这一结论的准确性。

关键词：动生电动势；安培力做功；回路消耗的电功率

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2015）4-0040-4

1 明确一个常用结论成立的条件

导体棒在磁场中做切割磁感线运动时，产生电流，受到磁场对其的作用力——安培力。在平时的教学中，经常提及在该切割过程中存在相应的功能关系：“导体棒切割磁感线以稳定速度运动时，电路获得的电功率等于导体棒克服安培力做功功率。”该结论是否正确？如果有瑕疵，应该如何修正？现对该结论作如下推导。

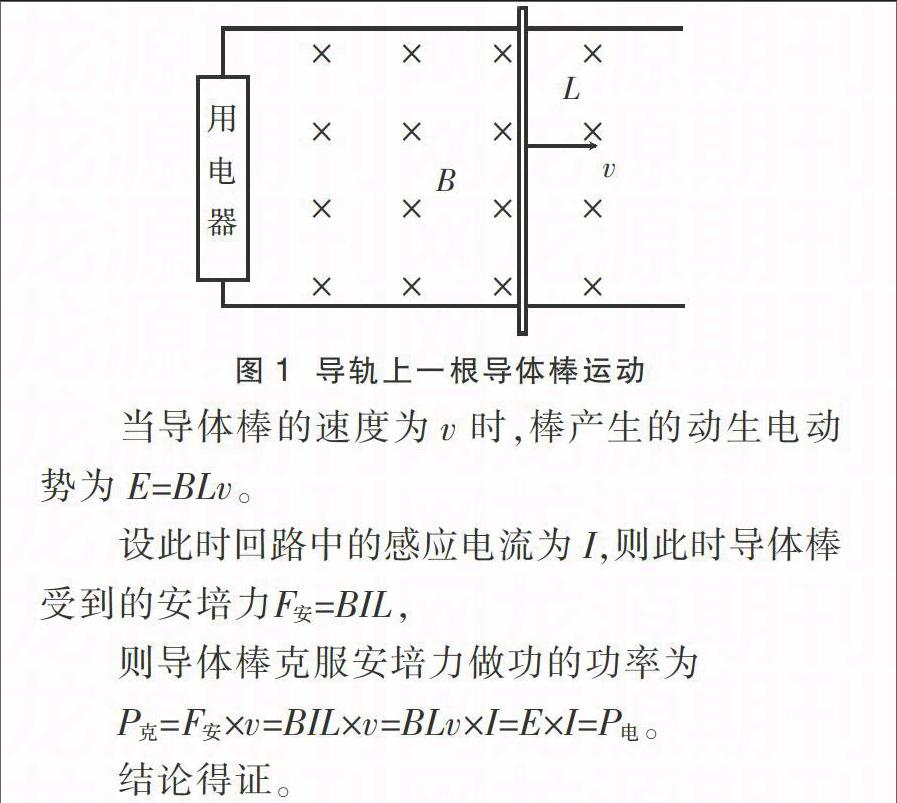
在图1所示的电路中，磁感应强度大小为B的匀强磁场垂直纸面向里，长为L的导体棒在外力F的作用下沿导轨运动。

当导体棒的速度为v时，棒产生的动生电动势为E=BLv。

设此时回路中的感应电流为I，则此时导体棒受到的安培力F安=BIL，

则导体棒克服安培力做功的功率为

P克=F安×v=BIL×v=BLv×I=E×I=P电。

结论得证。

但这里有必要作相应的说明：

①图1中的“用电器”不一定是电阻。它可以是电阻，亦可以是电容、电感，甚至可以里面包含电源。若如此，导体棒中的电流也不一定就是全部由导体棒切割磁感线产生的动生电动势产生，所以导体棒中的电流方向不一定朝上或者朝下，当然导体棒受到的安培力也就不一定是做负功。

②动生电动势为E=BLv，该式的磁感应强度B，导体棒L，切割速度v，三者均是矢量，要使公式成立的条件是三者两两垂直。安培力F安=BIL成立的条件也要磁感应强度B和导体棒L相互垂直。根据安培力规律，安培力一定跟磁感应强度B和导体棒L决定的平面垂直。因此，在我们讨论的这个“结论”的范围内，这根导体棒受到的安培力一定与它的切割速度在一条直线上，但方向可能相同，也可能相反。

③不论是动生电动势E=BLv中的速度，还是安培力的功率为P克=F安×v中的速度，它们均是瞬时速度。因此，上述等式成立的条件不需要导体棒作稳定的运动。

④从上面的推导中，表面上看不要其他额外的条件等式一定成立。但仔细推敲，上述等式成立一定要有两个条件。其一，电动势E=BLv中的速度是导体棒切割磁场的速度，这里隐含的意思是，这个速度的参照物是磁场（应该是产生磁场的物体或者物质）；而安培力的功率为P克=F安×v中速度的参照物没有特别说明的话就是地面。因此，要使等式BIL×v=BLv×I成立，这两个速度除了要满足方向关系外，还要是同一个参照系内讨论的两个速度，或者说磁场B相对地面是静止的；其二，要使等式BLv×I=E×I成立，这个电动势E一定是导体棒切割磁感线产生的BLv，不能张冠李戴，因为在电路中可能存在其他的电源。如，可能是导体棒切割磁感线产生的动生电动势，也可能存在感生电动势，甚至存在其他电源。

2 利用三种情形来对上述结论作具体研究

情形1：两根导体棒以不同的速度做切割磁感线运动

如图2所示，两根无限长金属导轨MN、PQ水平地平行放置，相距L，质量均为m的光滑金属棒ab、cd垂直置于导轨上。在导轨间的电阻均为R，导轨电阻不计，整个装置处在磁感应强度为B的竖直向下的匀强磁场中（图中未画出）。现对ab棒施加一个平行于导轨、方向水平向右的恒力F作用，cd棒会向右运动。设某一时刻ab棒的速度为v1，cd棒的速度为v2，求此时：

①安培力对cd棒做功的功率Pcd；

②ab棒克服安培力做功的功率；

③电路中产生的电功率P电。

讨论

①因为P电ab=P安1，所以电路中的电流不等于ab棒上产生的动生电源单独作用时产生的电流，但这不影响结论“作切割磁感线的棒中的动生电源提供的电功率等于该棒克服安培力做功功率”的成立。当然，对cd棒来说也是如此。

②cd棒受到的安培力对cd棒做正功。而电流流过cd棒时，是由cd棒上感应电源的正极流入，负极流出的，因此该电流是在给该电源“充电”，其“充电”的方式是通过增加该棒的动能来实现的。可以设想，如果棒ab瞬间停止，cd棒将把它具有的动能全部转化为回路中的电能，电能再通过电流做功转化为焦耳热，以实现“充电”电能的转化。

③根据上面分析，此时电路中焦耳热的热功率为：

可以看出ab棒上的动生电源“提供”的电功率等于电路中的焦耳热的热功率与cd棒上的动生电源“充电”的电功率之和，即

P电=P电ab=PQ+P电cd。

注意：不要误把电路中的焦耳热的热功率等同于电路中产生的电功率，因为该电路不是纯电阻电路。

情形2：导体棒在运动磁场中做切割磁感线运动

（2007年上海物理高考试题）如图3（a）所示，光滑的平行长直金属导轨置于水平面内，间距为L、导轨左端接有阻值为R的电阻，质量为m的导体棒垂直跨接在导轨上。导轨和导体棒的电阻均不计，且接触良好。在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场，磁感应强度大小为B。开始时，导体棒静止于磁场区域的右端，当磁场以速度v1匀速向右移动时，导体棒随之开始运动，同时受到水平向左、大小为f的恒定阻力，并很快达到恒定速度，此时导体棒仍处于磁场区域内。

①求导体棒所达到的恒定速度v2；

②为使导体棒能随磁场运动，阻力最大不能超过多少？

③导体棒以恒定速度运动时，单位时间内克服阻力所做的功和电路中消耗的电功率各为多大？

④若t=0时磁场由静止开始水平向右做匀加速直线运动，经过较短时间后，导体棒也做匀加速直线运动，其v-t关系如图3（b）所示，已知在时刻t导体棒的瞬时速度大小为vt，求导体棒做匀加速直线运动时的加速度大小。

分析与解 该情形的①、②、④的分析与解略，我们重点分析问题③。

假设导体棒以速度v2匀速运动。需要强调的是，导体棒切割磁感线的速度的参考系为磁场（更确切地讲是产生该磁场的磁体，或载流体等）。因此，棒中感生电动势为E=BL（v1-v2）。导体棒中的电流为：

讨论

①不论导体棒以恒定速度运动，还是以变速运动，也不论磁场是否做匀速运动，上述关于P电、PF安的计算结果均成立，因为计算结果中的速度均是瞬时速度。当然要使克服摩擦力的做功功率等于棒受到的安培力的功率，那导体棒必须做匀速运动。

②从上述分析中可以明显看出导体棒提供的电功率不等于导体棒受到的安培力做功功率。原因就是因为瞬时功率中的速度，它的参考系在没有特别说明的情况下是地面，而动生电动势中的速度的参考系就是磁场。当两个参考系发生相对运动时，导体棒中动生电源提供的电功率就不会等于该导体棒受到的安培力的做功功率。如果我们令v1=0，则可以看到两个功率又会相等。而且是动生电源功率为正，即电源在提供电功率；而安培力功率为负，说明通过安培力做功正在将其他形式的能转化为电能。

情形3：回路中动生电动势和感生电动势共存

如图4所示，足够长的两光滑导轨平行水平放置，两条导轨相距为d，左端用阻值为R的导体MN相连，金属棒ab可在导轨上滑动，金属棒ab及导轨的电阻不计。整个装置处于竖直向下的均匀磁场中，磁场的磁感应强度随时间均匀增加，B=kt，其中k为大于零的常数。t=0时，金属棒ab与MN相距非常近，金属棒ab在水平外力F的作用下，在t=t0时回路的面积为S，此时金属棒的速度为v。求此时闭合回路消耗的电功率。

讨论

①动生电动势的产生原因是金属导体中的电子在随金属棒运动时受到洛伦兹力而发生定向移动，因此动生电动势的非静电力与洛伦兹力有关。而感生电动势的产生原因是变化的磁场产生了感生电场，在感生电场的作用下回路中的电子作定向移动，因此是电子受到的感生电场力充当感应电动势的非静电力。所以，动生电动势与感生电动势两者的非静力有明确的区别，洛伦兹力不做功，感生电场力做功。

②动生电动势是由金属棒切割磁感线产生的，它分布“在金属棒中”。而感生电动势是由感生电场产生的，它分布“在整个回路中”，而且即使没有回路，感生电场依然存在。从上面的分析中可以看出金属棒克服安培力的做功功率与回路中的电功率不相等。但如果将感生电动势kS去掉，即磁场不随时间发生变化，那么两个功率依然相等。

3 结 论

根据上面的分析得到以下结论：在高中阶段，当磁场相对地面静止且不随时间变化时（当然，磁场的磁感应强度可以随空间发生变化），导体棒中动生电动势的电功率与其所受的安培力的做功功率的绝对值相等。

参考文献：

[1]赵凯华，陈熙谋.电磁学[M].北京：高等教育出版社，2006.

[2]郭如松.安培力做功的“桥梁”作用及其引发的思考[J].物理教学探讨，2009，（10）：42.

（栏目编辑 罗琬华）