移动水声通信多径传输非一致多普勒估计方法研究

王 彪 支志福戴跃伟

(江苏科技大学电子信息学院 镇江 212003)

移动水声通信多径传输非一致多普勒估计方法研究

王 彪 支志福*戴跃伟

(江苏科技大学电子信息学院 镇江 212003)

现有水声通信中的多普勒估计方法一般都假定多径信道每条路径的多普勒因子相等，当各路径多普勒因子存在差异时，该类方法往往无法正确估计出每径的多普勒因子，导致补偿后的信号存在较大误差。为此该文在分析水声信道稀疏特性的基础上，提出一种基于稀疏表示理论的非一致多普勒估计方法。该方法结合水声多径信道与非一致多普勒稀疏特性生成包含信道信息的超完备字典，将每径的非一致多普勒因子估计转化为基于超完备字典的稀疏重构求解，实现非一致多普勒因子的准确估计。仿真结果表明，所提方法不仅能估计出差异较大的非一致多普勒因子，而且对于大多普勒频偏的估计也相当有效，特别适合于高速移动水声通信中的多普勒估计。

水声通信；多普勒估计；多径传输；稀疏表示

1 引言

由活动和静止节点共同构成的水声数据通信网是当今水声通信的发展趋势，而移动水声通信是网络化发展的必要技术[1]，所以高速移动水声通信代表了未来水声通信的发展方向。而且不同于陆地上的无线电通信，水声通信是典型的宽带通信[2]，其多普勒扩展程度更加严重，导致现有很多成熟的多普勒估计方法无法直接应用于水声通信。因此，在水声移动通信中，为了保证通信的正常工作，准确地实现多普勒因子的估计显得尤为重要。

对于水声通信中的多普勒估计问题，国内外有关学者作了大量研究，其中比较典型的方法是文献

[3]中所提到的两种的方法，即模糊度函数方法与块多普勒估计方法。随后出现一些以这些方法为基础的改进方法[4-6]，这类方法可统称为基于相关运算的方法，也是目前最常用的多普勒因子估计方法，文献[7]对这类方法的原理及性能进行了详细分析。另外，也有些学者将一些新的信号处理技术引入水声通信来进行多普勒估计，如基于分数阶傅里叶变换的估计方法[8]、基于部分傅里叶变换的间接方法[9]等。文献[10]提出了一种水声扩频通信多普勒估计与补偿方法，但此方法的实现过程不具有一般性。以上这些方法一般都适用在多径多普勒扩展不太严重且各径多普勒因子一致相等的场合，对于每条路径的多普勒因子差异较大的非一致多普勒信道，这些方法往往不能正确估计出每条路径的多普勒因子，而且当多普勒因子较大时，估计精度也不高，不适合于高速移动条件下的水声通信。

近年来，有少数文献[11-13]开始关注移动水声通信中的非一致多普勒扩展问题，移动多径水声通信系统中，每条路径对应不同的多普勒因子更加符合水声通信的实际情况，非一致多普勒扩展在水声通信中更具有一般性。另一方面，随着稀疏表示理论的不断发展以及它在图像及信号处理方面的广泛应用[14]，越来越多的学者考虑将它应用于水声信道的研究中[15-17]，取得了不错的效果。文献[15]，文献[16]的共同点都是将水声信道估计问题建模为稀疏表示问题，其中文献[15]侧重于比较各类算法的信道参数估计分辨率，文献[16]讨论在表面重力波占主导作用时水声信道的参数估计问题，没有考虑相对运动引起的信号压缩或扩展效应。它们提供了一种很好的研究思路，但是对于一致与非一致多普勒估计问题未作细致分析。

针对上述问题，本文从水声信道的稀疏特性出发，基于超完备字典将非一致多普勒估计问题建模为稀疏表示问题，利用稀疏重构算法中的压缩采样匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP)算法[18]对模型求解，通过时延来具体确定多普勒因子所属路径，实现水声非一致多普勒估计。仿真结果表明，所提方法不仅能够实现一致性多普勒估计，而且对于差异较大的非一致性多普勒扩展，也能够精确估计出每径的多普勒因子，且抗噪能力较高。

2 基于稀疏表示的非一致多普勒因子估计方法

目前经常使用的常规一致性多普勒估计方法大都是基于相关的多普勒估计方法[3]，该类方法通常采用如图1所示的发射信号帧结构，中间是数据信息，首尾是两个完全相同的线性调频(Linear Frequency Modulation, LFM)信号，在接收端通过比较一帧收发信号的时间间隔变化来估计多普勒因子的大小。

图1 常用相关估计方法帧结构

但是这种方法只适用于单径或各径多普勒因子相等的多径信道，对于某些水声信道，比如高速移动条件下的点对点水声通信、多用户系统中的移动水声通信[11]，信道快速时变，各径多普勒因子不再相等且频偏较大，此时若使用常规基于相关的多普勒估计结果进行多普勒补偿会造成残余多普勒过大，接收机无法正确解调。而本文所提如下非一致多普勒估计方法能够精确估计出每径的多普勒因子，这样更加有利于补偿，提高通信的可靠性。

2.1 信道与系统模型

移动水声通信信道本质上是双扩展的[2]，同时具有时延扩展与多普勒扩展，其时变多径冲激响应通常描述为

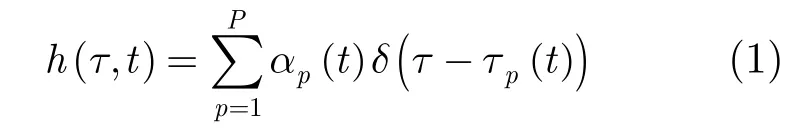
式中，αp(t )为第p条路径的时变幅度衰减，τp(t)为对应的时变路径时延，它们都体现出信道的时变性。对于本文所研究的问题，同步信号持续时间较短，在一个同步脉冲持续时间内，τp(t )和αp(t)可作如下合理近似[4,5]：

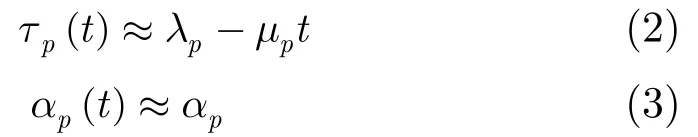
式(2)和式(3)中，pλ为初始路径时延因子，pμ为第p条路径的多普勒因子，每条路径是不同的。将式(2)，式(3)代入式(1)，得时变多径信道模型为

假定发送信号为()st，经过上述时变多径信道后输出信号为

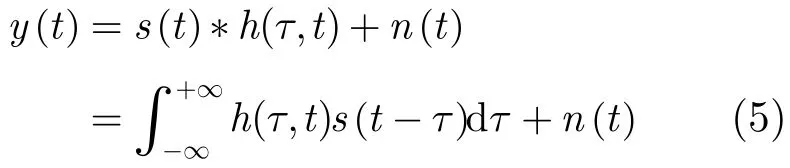
式中∗表示线性卷积，()nt表示高斯白噪声，将式(4)代入式(5)，可得接收端接收信号：

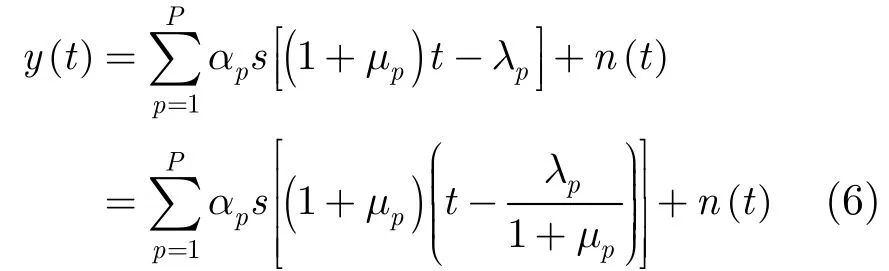
为方便表示，设等效时延τp=λp/(1+μp)、等效多普勒因子νp=1+μp(由此式可以看出，等效多普勒因子比文献[3]中定义的多普勒因子大1，以后提到的多普勒因子均指的是等效多普勒因子)，则式(6)变为

本文所提多普勒估计方法假设各径的等效多普勒因子pν具有不同值，下面从理论上来推导这种非一致的多普勒因子估计原理。

2.2 原理推导

为对式(7)进行离散化处理，定义如下的pν,pτ参数集合：

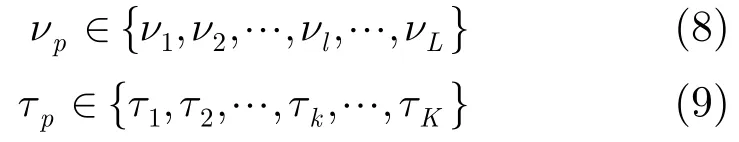
其中νl=ν1+(l -1)Δν,τk=τ1+(k -1)Δτ,Δν, Δτ表示多普勒及时延估计的离散精度，可以根据需要灵活调整，L,K分别表示可能的多普勒因子、时延值个数。利用式(8)，式(9)得式(7)的离散形式为

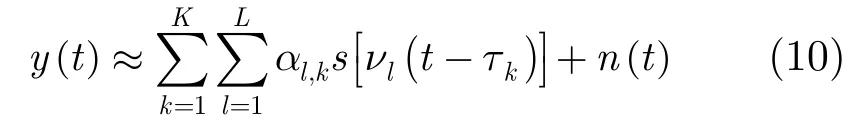
设()st的持续时间为[]0,T，在接收端对()yt以间隔tΔ进行抽样，第i个抽样值为

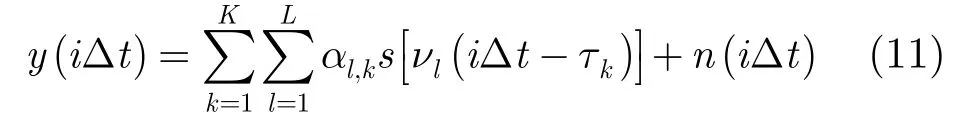
令式(9)中τ1=0，抽样间隔Δt=Δτ，并省略式(11)中的Δt，得其简化形式为

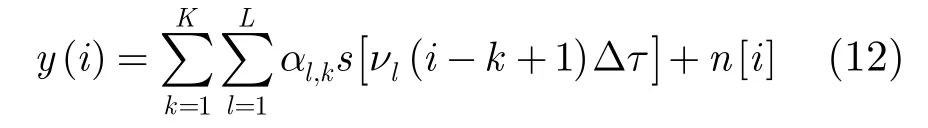
将式(12)写成向量形式，得

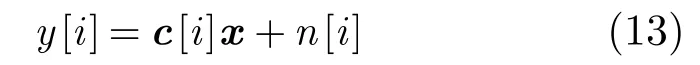
式中

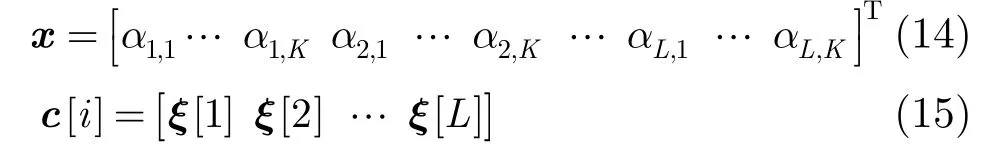
式(15)中

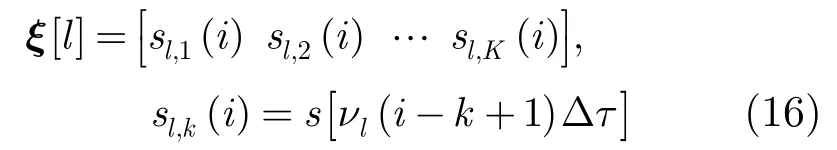
将接收端在[]0,T内的所有抽样值累积，得到式(7)的矩阵

式中

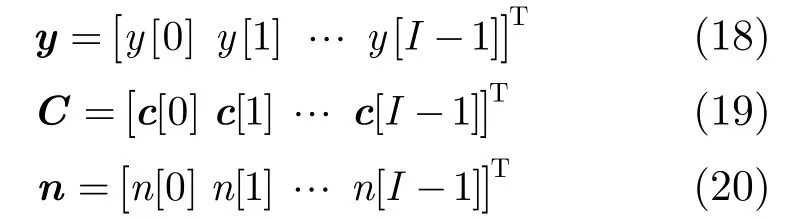
式(17)中y为I维的接收向量，C为I×(L×K)维矩阵，称之为超完备字典，对于接收端来说是已知的，n为I维的高斯白噪声向量，I=T/Δt为接收信号的采样数目。

考虑式(17)所示接收信号的向量形式，接收向量可以看作以x元素为系数的C各列的线性组合。分析式(15)，式(16)发现，C的每一列中sl,k(·)有相同的下标(l,k)，恰好对应式(8)，式(9)中某种可能的多普勒与时延νl, τk，而x是相应的幅度衰减因子。在已知y与C的前提下，如果能从式(17)中求出x，则进而可得该条路径所对应的等效多普勒因子与时延，从而达到多径非一致多普勒估计的目的。

2.3 基于超完备字典的稀疏重构算法

注意到水声信道的稀疏结构[16]，即多径信道中只有少部分能量比较强的路径能够到达接收端被接收机处理，大部分信道能量集中在少数时延与多普勒值上，反应到信道模型上就是式(17)中x的元素大量为0，只有少数非零值，对应于那些比较强的多径。

对于本文所研究问题，y从接收信号抽样得到，字典C可由收发双方共知的探测信号()st按一定精度预先生成，它们都是已知的。由于字典精度很高，C的行数远远小于它的列数，即IKL×≪，未知数的个数远远大于方程的个数，因此式(17)是个欠定方程，有无穷多解[14]。但是由于水声信道的稀疏特点，x中大量元素为0，则可以利用稀疏表示理论来求解该欠定方程，重构稀疏向量x，进而找到该条路径所对应的等价多普勒因子，这正是本文进行多普勒估计的核心思想。

目前，稀疏表示理论中有多种重构算法，包括比较著名的贪婪追踪算法[14]，如BP(基追踪)，MP(匹配追踪)，OMP(正交匹配追踪)算法等，以及凸优化算法等。稀疏表示理论中的CoSaMP算法[18]由于其建立在回溯思想上，同时结合了贪婪追踪算法与凸优化算法的优点，且容易实现，稳定性和鲁棒性优于一般的稀疏重建算法，故本文侧重于使用CoSaMP算法通过重构x来实现水声信号的多普勒因子估计，CoSaMP算法的原理这里不再进行详细说明，可参考文献[18]。 以下将结合上述理论推导和分析，给出本文所提出的非一致多普勒估计方法的具体步骤。

2.4 非一致多普勒估计步骤

基于超完备字典和稀疏表示理论的水声多径非一致多普勒因子估计方法实现步骤如下：

第..1.步 由接收双方都已知的探测信号()st，结合信道特点，选取合适精度，构造超完备字典C。

第2步 选择合适的抽样周期Δt对接收信号y(t)进行采样，得到接收信号向量y。

第3步 由字典C，接收向量y，稀疏度P(即可能的多径数目)，利用CoSaMP算法，重构x。

第4步 找到x中非零元素所对应字典C中的相应列，继而找到各径所对应的等价多普勒因子。

在以上步骤的基础上，其具体的实现算法如表1所示。

表1 基于CoSaMP算法的非一致多普勒估计步骤

3 仿真与性能分析

下面通过仿真来验证本文方法的可行性与有效性。仿真采用如下的LFM信号：

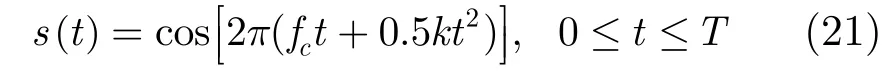
对应的复等效低通信号为

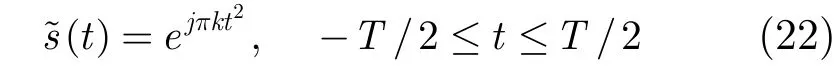
其中fc=800 Hz 为LFM信号的调制频率，k= 400 Hz/s为调制率，T为脉冲持续时间，这里设为0.5 s，相应的频宽范围800～1000 Hz。实验假定水声信道为5条多普勒扩展比较严重的非一致性多普勒扩展信道，5条路径的多普勒因子各不相同且差异较大，信道参数设置如表2所示。

设抽样间隔Δt为0.5 ms，采样点数I=T/ Δt+1=1001，式(8)中最小等价多普勒因子νmin= ν1=0.85，最大因子νmax=νL=1.15，估计精度Δν=0.005, L=(νL-ν1)/Δν+1=61；类似地，设式(9)中τmax=15 ms,Δτ=Δt=0.5ms,K=τmax/Δτ+1=31。下面将通过以下仿真来分析本文方法性能。

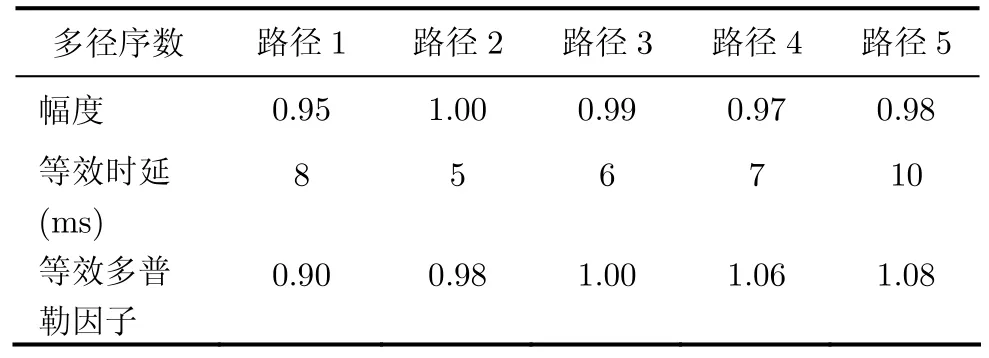
表2 信道参数设置

仿真1 无噪与有噪情况下本文方法的估计结果

为了分析噪声对本文方法的影响，对无噪声和含噪声两种情况进行了仿真，并给出了估计结果的3维与2维图形显示，分别如图2和图3所示，其中图3所示的信噪比(Signal to Noise Ratio, SNR)为6 dB时的估计结果。由3维图形可以清楚地看到不同时延路径所对应的不同多普勒因子与幅度衰落结果。分析图2与图3可以发现，在无噪声与SNR为6 dB两种情况下，尽管每条路径的多普勒因子差异较大，但是本文方法都能够准确无误地估计出每条路径的多普勒因子。另外，由图3(a)与图2(a)可以看出，在有噪声的情况下，重构的幅度衰减因子发生一定误差，但它只是一个中间结果，表明其对应路径能量较强，对于多普勒估计结果没有任何影响，图3(b)估计结果的正确无误也证实了这一点。

仿真2 估计精度随信噪比的变化

采用如表2所示的非一致多普勒估计参数，由于每条路径的多普勒因子差异较大，仿真表明基于相关的多普勒估计方法[3]失效，而本文方法能够适用于非一致多普勒估计情况。图4给出了本文方法平均每径估计错误随SNR的变化曲线图。其中平均每径估计错误(AVE)定义为

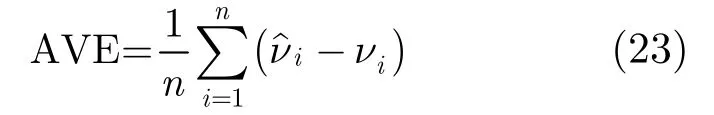
式中n为多径数目，本次仿真为5,νˆi,νi分别为每条路径等价多普勒因子的估计值与真实值，在每条路径多普勒因子差异较大情况下，该式用来衡量本文方法估计结果的综合性能。通过图4可以看出，当SNR高于3 dB时，本文方法仍然能够正确无误地进行多普勒估计，而当SNR低于3 dB时，估计误差大致在10-3数量级，也在实际工程的接受范围内，说明该方法具有较高的抗噪性能。

仿真3 各径多普勒因子一致时，本文方法与常规方法的对比分析

本文方法也适用于一致且因子较大的多普勒情况，为了验证本文方法对一致多普勒因子的估计性能，并与常规基于相关的一致性多普勒估计方法进行比较，我们仿真了具有相同多普勒因子采样两种不同方法的估计结果，并且仿真了多普勒因子分别是1.01, 1.02, 1.03三种情况下的均方根误差(Root Mean Squared Error, RMSE)随信噪比的变化曲线，如图5所示。其中RMSE定义为

图2 无噪声下的估计结果

图3 SNR为6 dB时的估计结果

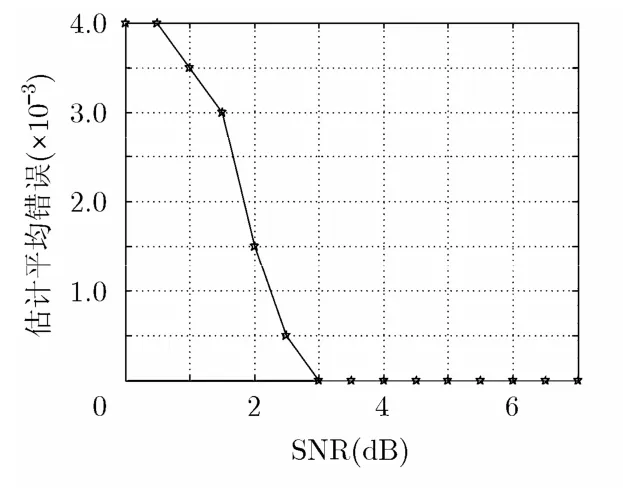
图4 不同信噪比下平均每径估计错误

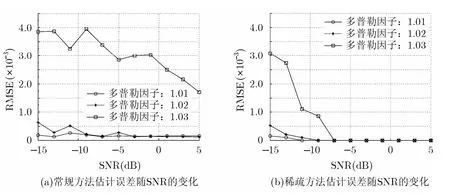
图5 本文方法与常规方法的对比

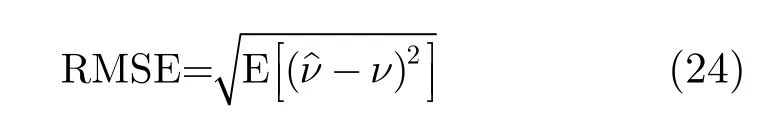
4 结论

本文针对水声移动通信多径信道中非一致多普勒扩展问题，开展了基于稀疏表示理论的多普勒因子估计方法研究，系统地介绍了所提出的多普勒因子估计算法的原理，详细地给出了具体实现步骤，并通过仿真实验验证了本文方法的如下特点：(1)非常适合多径传输差异较大的非一致性多普勒因子估计，且具有较高的抗噪能力；(2)对于常规一致多普勒扩展，也能够以较低的信噪比实现大多普勒频偏下的多普勒因子估计。因此，本文方法特别适合于信道时变性较强的高速移动水声通信的多普勒估计。

[1] 殷敬伟. 水声通信原理及信号处理技术[M]. 北京: 国防工业出版社, 2011: 234-235.

Yin Jing-wei. Principle of Underwater AcousticCommunication and Techniques of Signal Processing[M]. Beijing: National Defense Industry Press, 2011: 234-235.

[2] Ebihara T and Mizutani K. Underwater acoustic communication with an orthogonal signal division multiplexing scheme in doubly spread channels[J]. IEEE Journal of Oceanic Engineering, 2014, 39(1): 47-58.

[3] Sharif B S, Neasham J, Hinton O R, et al.. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2000, 25(1): 52-61.

[4] Mason S F, Berger C R, Zhou S, et al.. Detection, synchronization, and Doppler scale estimation with multicarrier waveforms in underwater acoustic communication[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(9): 1638-1649.

[5] Li B, Zhou S, Stojanovic M, et al.. Multicarrier communication over underwater acoustic channels with nonuniform Doppler shifts[J]. IEEE Journal of Oceanic Engineering, 2008, 33(2): 198-209.

[6] Berger C R, Zhou S, Preisig J C, et al.. Sparse channel estimation for multicarrier underwater acoustic communication: from subspace methods to compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1708-1721.

[7] Wan L, Wang Z, Zhou S, et al.. Performance comparison of Doppler scale estimation methods for underwater acoustic OFDM[J]. Journal of Electrical and Computer Engineering, Special Issue on Underwater Communications and Networks, 2012, DOI: 10.1155/2012/703243.

[8] Zhang X, Han X, Yin J W, et al.. Study on Doppler effects estimate in underwater acoustic communication[J]. The Journal of the Acoustical Society of America, 2013, 133(5): 3463-3463.

[9] Aval Y M and Stojanovic M. Partial FFT demodulation for coherent detection of OFDM signals over underwater acoustic channels[C]. Proceedings of MTS/IEEE Oceans Conference, Bergen, Norway, 2013: 1-4.

[10] 袁兆凯, 隋天宇, 李宇, 等. 水声扩频通信中多普勒估计与补偿算法研究[J]. 电子与信息学报, 2012, 34(1): 51-56.

Yuan Zhao-kai, Sui Tian-yu, Li Yu, et al.. The estimation and compensation of Doppler effect on underwater acoustic spread spectrum communication[J]. Journal of Electronics & Information Technology, 2012, 34(1): 51-56.

[11] Tu K, Duman T M, Stojanovic M, et al.. Multiple-resampling receiver design for OFDM over Doppler-distorted underwater acoustic channels[J]. IEEE Journal of Oceanic Engineering, 2013, 38(2): 333-346.

[12] Karakaya B, Hasna M O, Duman T M, et al.. Multi-resampling Doppler compensation in cooperative underwater OFDM systems[C]. Proceedings of MTS/IEEE Oceans Conference, Bergen, Norway, 2013: 1-8.

[13] Yerramalli S and Mitra U. Optimal resampling of OFDM signals for multiscale-multilag underwater acoustic channels [J]. IEEE Journal of Oceanic Engineering, 2011, 36(1): 126-138.

[14] Elad M. Sparse and Redundant Representations: from Theory to Applications in Signal and Image Processing[M]. New York: Springer, 2010: Chapter 9-11.

[15] Jiang X, Zeng W J, and Li X L. Time delay and Doppler estimation for wideband acoustic signals in multipath environments[J]. The Journal of the Acoustical Society of America, 2011, 130(2): 850-857.

[16] Byun S H, Seong W, and Kim S M. Sparse underwater acoustic channel parameter estimation using a wideband receiver array[J]. IEEE Journal of Oceanic Engineering, 2013, 38(4): 718-729.

[17] Qu Feng-zhong, Nie Xing-yang, and Xu Wen. A two-stage approach for the estimation of doubly spread acoustic channels[J]. IEEE Journal of Oceanic Engineering, 2014, DOI: 10.1109/JOE.2014.2307194.

[18] Needell D and Tropp J A. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301-321.

王 彪： 男，1980年生，博士，副教授，研究方向为水声通信.

支志福： 男，1990年生，硕士生，研究方向为水声通信.

戴跃伟： 男，1962年生，博士，教授，博士生导师，研究方向为信息处理与隐藏.

Study on Non-uniform Doppler Estimation for Underwater Acoustic Mobile Communications with Multipath Transmission

Wang Biao Zhi Zhi-fu Dai Yue-wei

(School of Electronic and Information, Jiangsu University of Science and Technology, Zhenjiang 212003, China)

The existing methods of Doppler estimation in UnderWater Acoustic (UWA) communication generally assume that the Doppler factor of each path is equal in multipath channel. But when the Doppler factors are different from each other, such methods can not estimate the Doppler factor correctly, resulting in significant compensation error. By analyzing the sparsity of the UWA channel, a novel method of non-uniform Doppler estimation is proposed, which is based on the sparse representation theory. By using the over-complete dictionary combining UWA multipath channel and non-uniform Doppler sparsity, the method transforms Doppler estimation of each path into sparse solution reconstruction, achieving accurate estimation of non-uniform Doppler factor. Simulation results show that the proposed method can estimate not only the quite different Doppler factors but also the large Doppler frequency offset. Therefore, it is especially important for Doppler estimation in high-speed mobile UWA communication.

Underwater acoustic communication; Doppler estimation; Multipath transmission; Sparse representation

TN929.3

A

1009-5896(2015)03-0733-06

10.11999/JEIT140665

2014-05-21收到，2014-09-12改回

国家自然科学基金(11204109)，江苏省高校自然科学基金(12KJB510003, 13KJB510007)，江苏省高校优势学科项目和江苏省“青蓝工程”项目资助课题

*通信作者：支志福 bozhou1990@163.com