基于稀疏稠密结构表示与在线鲁棒字典学习的视觉跟踪

袁广林薛模根

①(解放军陆军军官学院十一系 合肥 230031)

②(解放军陆军军官学院科研部 合肥 230031)

③(合肥工业大学计算机与信息学院 合肥 230009)

基于稀疏稠密结构表示与在线鲁棒字典学习的视觉跟踪

袁广林*①薛模根②③

①(解放军陆军军官学院十一系 合肥 230031)

②(解放军陆军军官学院科研部 合肥 230031)

③(合肥工业大学计算机与信息学院 合肥 230009)

L1跟踪对适度的遮挡具有鲁棒性，但是存在速度慢和易产生模型漂移的不足。为了解决上述两个问题，该文首先提出一种基于稀疏稠密结构的鲁棒表示模型。该模型对目标模板系数和小模板系数分别进行L2范数和L1范数正则化增强了对离群模板的鲁棒性。为了提高目标跟踪速度，基于块坐标优化原理，用岭回归和软阈值操作建立了该模型的快速算法。其次，为降低模型漂移的发生，该文提出一种在线鲁棒的字典学习算法用于模板更新。在粒子滤波框架下，用该表示模型和字典学习算法实现了鲁棒快速的跟踪方法。在多个具有挑战性的图像序列上的实验结果表明：与现有跟踪方法相比，所提跟踪方法具有较优的跟踪性能。

视觉跟踪；稀疏表示；稠密表示；字典学习

1 引言

视觉跟踪是计算机视觉中的基本问题之一，其目的是利用图像序列自动估计目标状态。视觉跟踪在运动分析、视频监控、车辆导航和人机交互等方面具有重要的应用价值。经过三十多年的研究，已经提出了一些跟踪方法[1-3]，但是目标遮挡、目标变化、复杂背景和快速性要求等难题使得视觉跟踪仍是计算机视觉领域的研究热点，鲁棒快速的视觉跟踪方法还没有解决。

近年来，基于稀疏表示的视觉跟踪得到了广泛关注[4]。受稀疏表示在人脸识别[5]中应用的启发，2009年，文献[6]首次将稀疏表示应用到视觉跟踪中，提出了L1跟踪。L1跟踪利用候选目标表示系数的稀疏性提升了子空间跟踪对目标遮挡的鲁棒性，因而受到了广泛的关注。但是表示系数的稀疏性也导致L1跟踪的速度较慢，并且易产生模型漂移，尤其是当模板中引入离群数据时会导致跟踪失败。针对L1跟踪的速度问题，文献[7]利用动态组稀疏提出一种两阶段稀疏优化视觉跟踪方法，该方法通过降低粒子特征的维数来提高L1跟踪的效率。文献[8]提出一种最小化误差界采样方法，通过减少L1最小化的求解次数提高L1跟踪的速度。文献[9]在L1最小化模型上增加小模板系数的L2范数正则化项，并设计了其快速算法，进一步提升了L1跟踪的速度与鲁棒性，但是它没有考虑视觉跟踪中表示系数的特殊稀疏结构。根据粒子在同一模板集上表示系数的相似性，文献[10]利用多任务稀疏学习联合求解粒子的表示系数，提高了L1跟踪的速度。为了适应目标表观的变化，在跟踪过程中要更新目标模板。文献[6,7,10]直接利用跟踪结果更新目标模板，使得离群数据引入到目标模板中，从而引起跟踪失败。针对L1跟踪的模型漂移问题，文献[11,12]用正交完备基代替L1跟踪中的过完备非正交基，提出一种基于小模板系数稀疏性约束的表示模型跟踪目标，提高了L1跟踪的鲁棒性。文献[8,9,11]利用小模板系数检测遮挡，根据检测结果更新目标模板。文献[12]根据小模板系数重建目标图像，利用重建图像更新目标模板。文献[8,9,11,12]中模板更新方法的问题在于小模板也能表示跟踪目标[9]，这时会导致遮挡检测失败。文献[13]利用块坐标下降优化原理提出了在线字典学习算法。为了解决离群数据对字典学习的影响，文献[14]提出一种在线鲁棒字典学习算法。从字典学习的角度看，模板更新是在线的字典学习问题，所以在线鲁棒字典学习为鲁棒模板更新提供了思路。

为了提高L1跟踪的速度，降低模型漂移的发生，本文首先提出一种基于稀疏稠密结构的鲁棒表示模型。该模型对小模板系数和目标模板系数分别进行L1范数和L2范数正则化，保证对遮挡目标跟踪的鲁棒性，同时又增强了对离群模板的鲁棒性。其次，基于块坐标优化原理，利用岭回归和软阈值操作快速求解候选目标的表示系数，提高了目标跟踪的速度。最后，在文献[13,14]的启发下，本文提出一种鲁棒字典学习算法用于模板更新，进一步降低了模型漂移的发生。在这3个方面的基础上，本文实现了基于稀疏稠密结构表示与在线鲁棒字典学习的快速鲁棒跟踪方法，用多个具有挑战性的图像序列验证了本文跟踪方法的时效性。

2 稀疏稠密结构鲁棒表示模型

L1跟踪用L1范数正则化最小二乘模型求解候选目标的稀疏表示系数，在粒子滤波框架下，以候选目标在目标模板上的重建误差作为观测似然跟踪目标。L1跟踪对目标遮挡具有鲁棒性的原因在于对表示系数的稀疏性约束。然而表示系数的稀疏性约束给L1跟踪带来了两个不足[4]：一方面，由于一次跟踪要求解较多L1最小问题，使得L1跟踪的速度较慢。为了提高L1跟踪的速度，现有方法[7-10]用低分辨图像跟踪目标，降低了目标跟踪的精度；另一方面，表示系数的稀疏性约束使得L1跟踪对模板中的离群数据较敏感，当目标模板中引入离群数据时，易发生跟踪失败。文献[15]的研究结果表明：表示系数的稀疏性不是提高人脸识别性能的真正原因，在使用过完备非正交字典表示人脸时，编码系数的L2范数约束也能保证较好的人脸识别性能。从上述分析可知：为了保证L1跟踪对目标遮挡的鲁棒性，要对小模板系数施加L1范数约束，为了保证L1跟踪对离群模板的鲁棒性，要对目标模板系数进行L2范数约束。据此，本文提出稀疏稠密结构鲁棒表示模型，如式(1)所示。

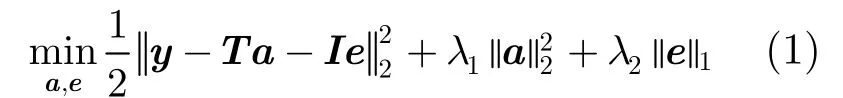
其中y∈Rd是候选目标，T=[t1,t2,…,tn]∈Rd×n是目标模板，I∈Rd×d称为小模板，是一个单位阵，a称为目标模板系数，是候选目标y在目标模板T上的表示系数，e称为小模板系数，是候选目标y在小模板I上的表示系数，||⋅||1和||⋅||2分别表示L1范数和L2范数，1λ和2λ是正则化参数。

稀疏稠密结构鲁棒表示模型式(1)有以下优点：首先，模型式(1)对小模板系数e进行L1范数约束，使得e具有稀疏性，这保证了对遮挡目标跟踪的鲁棒性。其次，对目标模板系数a进行L2范数约束，使得目标模板系数a具有稠密性，这样目标跟踪不依赖于少数几个模板，而是所有模板共同作用的结果，这提高了跟踪方法对模板中离群数据的鲁棒性，即使模板中存在离群数据仍能稳定跟踪目标。最后，基于块坐标优化原理[16]，利用岭回归和软阈值操作可以建立模型式(1)的快速求解算法，从而提高目标跟踪的速度。

3 稀疏稠密结构鲁棒表示快速算法

引理1 给定eopt，则

证明 假如已知eopt，则优化问题式(1)等价于。此问题是L范数2正则化最小二乘问题，目标函数对a求导数并令其等于零，即可得到aopt=(TTT+λ1I)-1TT(y-eopt)。

证毕

引理2 给定aopt，则eopt=Sλ2(y-Taopt)，其中Sτ(x)是软阈值操作，定义为Sτ(xi)≐sgn(xi)⋅max{|xi|-τ,0}, sgn(⋅)是符号函数。

证明 假如已知opta，则优化问题式(1)等价于此问题是凸优化问题，由文献[17]可知，其全局最优解可以通过软阈值操作Sτ(x)得到，即eopt=Sλ2(y-Taopt) 证毕

由引理1和引理2，并结合块坐标优化原理[17]可建立如表1所示的迭代算法求解优化问题式(1)的最优解。

我地的畜牧养殖业多集中在农村地区，基层养殖场、养殖户越来越多，交通的发展帮助养殖户更好的获取养殖利润，但也使得原本局限于某些地区的动物疫病还是蔓延和传播，甚至在传播过程中出现突变，为我地基层养殖业造成更大的伤害。农村基层动物防疫部门长期存在经费短缺问题，在动物疫病传播和突变频繁的当代，经费短缺问题更加突出，没有充足的设备、药品及防疫设施，为农村基层养殖业防疫工作造成极大的负面影响。

表1 稀疏稠密结构鲁棒表示快速算法

4 在线鲁棒字典学习

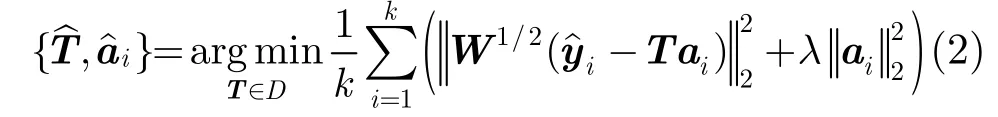
其中W是一个对角阵，其值,jjW是yˆi的第j个像素的权值，其它符号与式(1)相同。式(2)的求解包括编码和字典更新两个阶段。在编码阶段，固定字典T求解编码系数aˆi。字典T已知，式(2)是L2范数正则化最小二乘问题，用IR3C(Iteratively Reweighted Regularized Robust Coding)算法[18]求解aˆi。在字典更新阶段，固定编码系数aˆi更新字典T。由文献[14]知，可用块坐标共轭梯度下降算法逐行求解式(3)得到字典T。

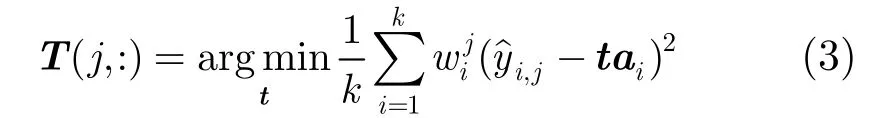
表2 在线鲁棒字典学习算法

表2 在线鲁棒字典学习算法

5 目标跟踪

5.1 粒子滤波

粒子滤波包括预测和更新两个步骤。假设y1:k-1={y1,y2,…,yk-1}为1到k-1时刻的所有图像观测，xk表示k时刻的目标状态，则预测过程为

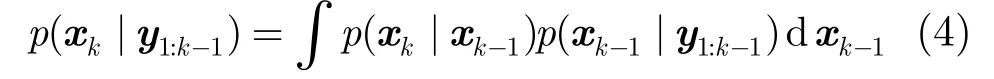
其中p(xk|xk-1)是动态模型。本文采用的动态模型为

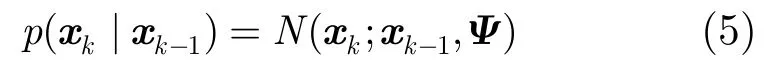
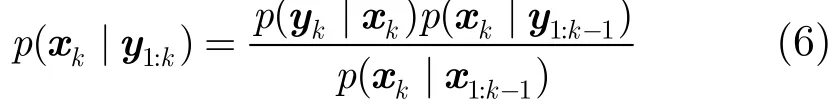
其中p(yk|xk)为观测模型。给定第i个粒子的图像观测，本文用算法1求解式(7)。

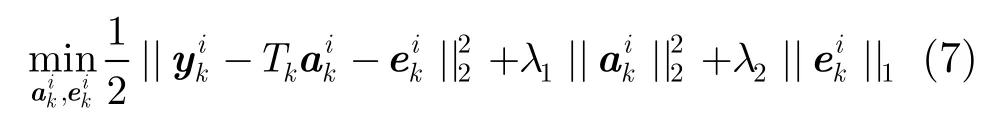
在此基础上，定义观测模型为

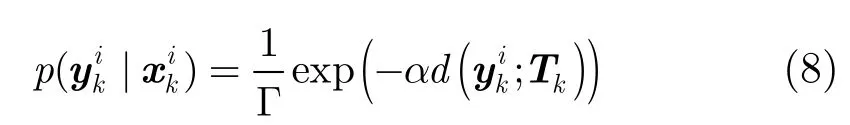
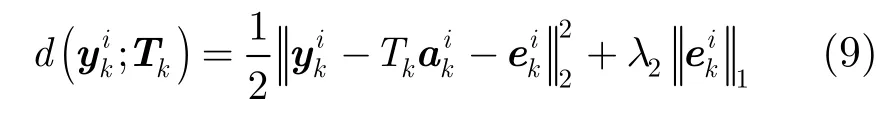
5.2 跟踪方法

以粒子滤波为框架，将动态模型、观测模型和在线鲁棒字典学习相结合建立跟踪方法如表3所示。

表3 跟踪方法

6 实验结果与分析

6.1 实验说明

以Matlab R2011b为开发工具，在Inter(R) Forth-Core 2.50 GHz CPU, 4G内存的台式机上，实现了本文提出的跟踪方法(简称L1L2跟踪)。用4个具有挑战性的图像序列[3]对本文L1L2跟踪进行了实验验证，并与IVT跟踪[1]，L1跟踪[6]和SP跟踪[11]进行了比较。实验中，目标的真实状态和其它4个跟踪方法在这4个测试序列上的跟踪结果由标准测试数据库得到[3]。本文L1L2跟踪的粒子数为600，正则化参数λ1和λ2分别是0.001和0.100，模板大小和个数分别为32×32和16，每隔5帧进行一次模板更新。

6.2 实验结果

图1给出了4个跟踪方法对4组测试序列的跟踪结果。faceocc1序列存在较大的目标遮挡，由于图1(a)可以看出，对于faceocc1序列，本文L1L2跟踪和L1跟踪的结果较优。david序列存在光照变化、out-plane旋转和尺度变化等诸多挑战，从图1(b)可以看出，对于david序列，本文L1L2跟踪和SP跟踪的结果优于其它两种跟踪方法。car4序列存在较大光照和尺度变化，由图1(c)可以看出，对于car4序列，本文L1L2跟踪、IVT跟踪和SP跟踪能够稳定跟踪目标，但是L1跟踪发生了跟踪漂移。jogging序列存在运动模糊、遮挡和变形等困难，从图1(d)可以看出，对于jumping序列，本文L1L2跟踪能够稳定地跟踪目标，其它跟踪方法均发生了失败。

本文利用跟踪成功率曲线下面积和成功率均值定量评价跟踪方法的性能[3]。假设目标的真实矩形区域和目标的跟踪结果矩形区域分别是ra和rt，则重叠得分定义为：，其中∩和∪分别表示区域的交集和并集。如果跟踪方法在一帧图像上的重叠得分S大于重叠阈值t0时，则认为该跟踪方法在这一帧图像上跟踪成功。据此定义跟踪方法在一个图像序列上的跟踪成功率为成功跟踪的图像帧数与序列图像总帧数的比值。给定一系列重叠阈值即可得到跟踪成功率曲线和成功率均值。图2和表4分别给出了4种跟踪方法在4个图像序列上的跟踪成功率曲线和成功率均值，由图2和表4可以看出，本文提出的L1L2跟踪方法优于其它3个跟踪方法。

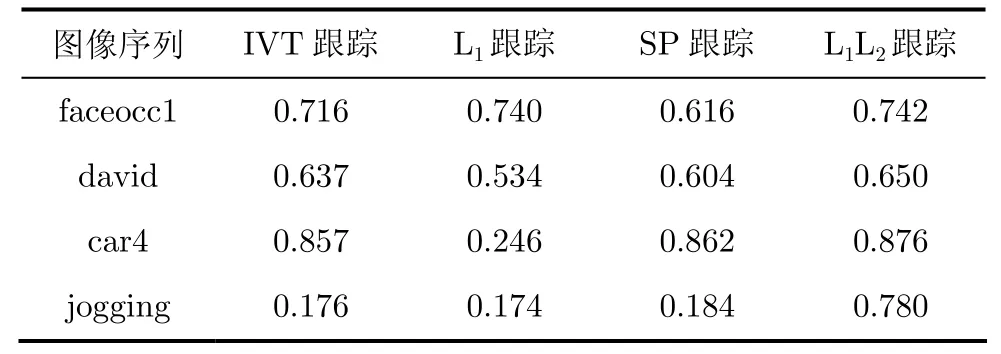
表4 跟踪成功率均值

假设U∈Rd×n是IVT跟踪和SP跟踪使用的特征基，T∈Rd×n是L1跟踪使用的目标模板，P∈Rd×n是算法1中的投影矩阵，k1是文献[11]中算

6.3 复杂性分析法1的迭代次数。由文献[1,6,11]可知，IVT跟踪，L1跟踪和SP跟踪的计算复杂度如表5所示。本文L1L2跟踪最耗时部分是用投影矩阵计算表示系数(算法1中的步骤3)，该计算是矩阵向量乘，其时间复杂度是O(k2dn)，其中，k2是算法1中的迭代次数。由上述分析可知：这4个跟踪方法的计算复杂度级别相同，都是变量多项式的复杂度。表5中第3和4列分别给出了在相同软硬件环境下，d=16×16和d=32×32，n=16时，求解一个样本表示系数的计算时间，可以看出，本文L1L2跟踪的速度比IVT跟踪慢，但是快于SP跟踪和L1跟踪。

图1 目标跟踪结果

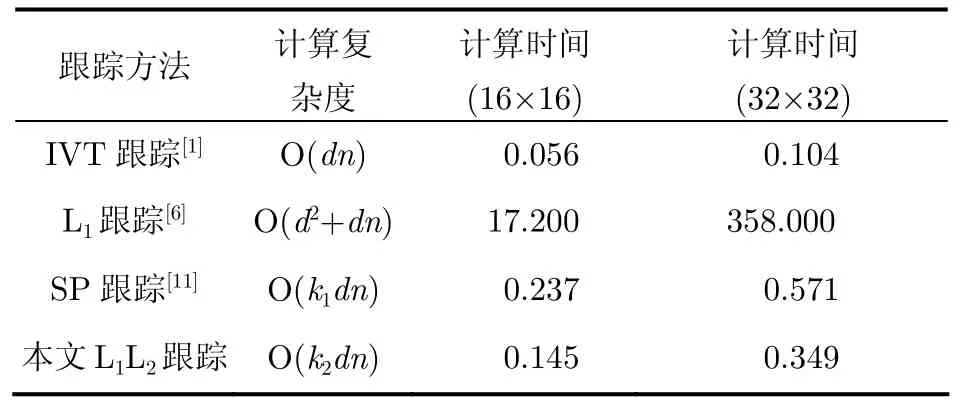
表5 计算复杂度与计算时间(ms)

6.4 讨论

与本文最相近的方法是SP跟踪[11]，它们均继承了L1跟踪[6]对小模板系数的稀疏性约束，这保证了对遮挡目标跟踪的鲁棒性。但是本文方法与SP跟踪有以下不同。第一是使用的模板基不同，本文方法用过完备基表示目标，SP跟踪用正交基表示目标。过完备基比正交基具有更优的表示能力已在人脸识别中[4]得到证实。第二是模板更新方法不同，本文方法用过完备基表示目标，可以用在线鲁棒字典学习算法更新模板，这抑制了离群数据对模板更新的影响，从而降低“模型漂移”的发生。SP跟踪用正交基表示目标并用增量主分量分析[1]更新特征基，不可避免地会引起“模型漂移”，从而降低目标跟踪的精度，甚至导致跟踪失败。图3和图4分别给出了SP跟踪的模板更新方法与本文模板更新方法对faceocc1序列跟踪在第600帧时的模板更新结果，可以看出，与SP跟踪的模板更新方法相比，本文模板更新方法的结果受离群数据的影响较小。第三是本文方法对目标模板系数进行L2范数约束，提高了对模板中离群数据的鲁棒性，即使模板中存在离群数据仍能稳定跟踪目标。正是由于上述3个方面的原因，使得本文方法的跟踪精度优于SP跟踪。

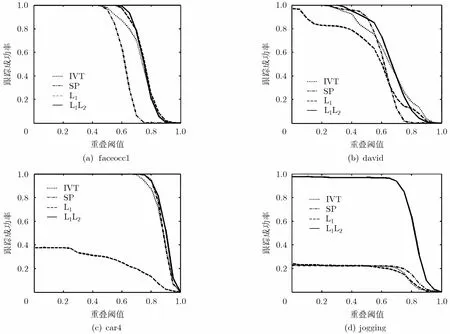
图2 跟踪成功率曲线

图3 SP模板更新结果

图4 本文方法模板更新结果

7 结论

本文提出一种稀疏与稠密结构表示模型，用于解决L1跟踪存在的速度慢和易受离群数据干扰的不足。对小模板系数进行L1范数约束保证了对遮挡目标跟踪的鲁棒性，对目标模板系数进行L2范数约束解决了L1跟踪易于受离群数据干扰的问题。基于块坐标优化原理，利用岭回归和软阈值操作设计了稀疏与稠密结构表示快速求解算法，提高了目标跟踪的速度。本文提出在线鲁棒字典学习算法实现模板更新，减小了离群数据对模板更新的影响，降低了模型漂移的发生。以粒子滤波为框架实现了基于稀疏稠密结构表示与在线鲁棒字典学习的的跟踪方法，在多个图像序列上的实验结果表明，本文跟踪方法优于现有跟踪方法。

[1] Ross D, Lim J, Lin R S, et al.. Incremental learning for robust visual tracking[J]. International Journal of Computer Vision, 2008, 77(1/2/3): 125-141.

[2] Kwon J and Lee K M. Visual tracking decomposition[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, 2010: 1269-1276.

[3] Wu Yi, Lim Jongwoo, and Yang Ming-hsuan. Online object tracking: a benchmark[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Portland, 2013: 2411-2418.

[4] Zhang Sheng-ping, Yao Hong-xun, Sun Xin, et al.. Sparse coding based visual tracking: review and experimental comparison[J]. Pattern Recognition, 2013, 46(7): 1772-1788.

[5] Wright J, Yang A Y, Ganesh A, et al.. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227.

[6] Mei X and Ling H B. Robust visual tracking using L1minimization[C]. Proceedings of IEEE InternationalConference on Computer Vision, Kyoto, 2009: 1436-1443.

[7] Liu Bai-yang, Yang Lin, Huang Jun-zhou, et al.. Robust and fast collaborative tracking with two stage sparse optimization[C]. Proceedings of Europe Conference on Computer Vision, Crete, 2010, Part IV: 624-637.

[8] Mei X, Ling H B, Wu Y, et al.. Minimum error bounded efficient L1tracker with occlusion detection[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Colorado, 2011: 1257-1264.

[9] Bao Cheng-long, Wu Yi, Ling Hai-bin, et al.. Real time robust L1tracker using accelerated proximal gradient approach[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Rhode Island, 2012: 1830-1837.

[10] Zhang Tian-zhu, Bernard Ghanem, Liu Si, et al.. Robust visual tracking via multi-task sparse learning[J]. International Journal of Computer Vision, 2013, 101(2): 367-383.

[11] Wang Dong, Lu Hu-chuan, and Yang Ming-hsuan. Online object tracking with sparse prototypes[J]. IEEE Transactions on Image Processing, 2013, 22(1): 314-325.

[12] Wang Dong, Lu Hu-chuan, and Yang Ming-hsuan. Least soft-thresold squares tracking[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Portland, 2013: 2371-2378.

[13] Mairal J, Bach F, Ponce J, et al.. Online learning for matrix factorization and sparse coding [J]. Journal of Machine Learning Research, 2010(11): 19-60.

[14] Lu Ce-wu, Shi Jian-ping, and Jia Jia-ya. Online robust dictionary learning[C]. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Portland, 2013: 415-422.

[15] Zhang Lei, Yang Meng, and Feng Xiang-chu. Sparse representation or collaborative representation: which helps face recognition?[C]. Proceedings of IEEE International Conference on Computer Vision, Colorado, 2011: 471-487.

[16] Tseng Paul and Yun Sangwoon. A block-coordinate gradient descent method for linearly constrained nonsmooth separable optimization[J]. Optimization Theory Application, 2009, 140(3): 513-535.

[17] Yang A Y, Ganesh A, Zhou Zi-han, et al.. A review of fast L1-minimization algorithms for robust face recognition[J]. IEEE Transactions on Image Processing, 2013, 22(8): 3234-3246.

[18] Yang Meng, Zhang Lei, Yang Jian, et al.. Regularized robust coding for face recognition[J]. IEEE Transactions on Image Processing, 2013, 22(5): 1753-1766.

袁广林： 男，1973年生，博士，讲师，主要研究方向为图像处理、计算机视觉、机器学习及其应用等.

薛模根： 男，1964年生，博士，教授，博士生导师，主要研究方向为图像处理、计算机视觉、光电防御等.

Visual Tracking Based on Sparse Dense Structure Representation and Online Robust Dictionary Learning

Yuan Guang-lin①Xue Mo-gen②③①(Eleventh Department, Army Officer Academy of PLA, Hefei 230031, China)
②(Department of Scientific Research, Army Officer Academy of PLA, Hefei 230031, China)
③(School of Computer and Information, Hefei University of Technology, Hefei 230009, China)

The L1trackers are robust to moderate occlusion. However, the L1trackers are very computationally expensive and prone to model drift. To deal with these problems, firstly, a robust representation model is proposed based on sparse dense structure. The tracking robustness is improved by adding an L2norm regularization on the coefficients associated with the target templates and L1norm regularization on the coefficients associated with the trivial templates. To accelerate object tracking, a block coordinate optimization theory based fast numerical algorithm for the proposed representation model is designed via the ridge regression and the soft shrinkage operator. Secondly, to avoid model drift, an online robust dictionary learning algorithm is proposed for template update. Robust fast visual tracker is achieved via the proposed representation model and dictionary learning algorithm in particle filter framework. The experimental results on several challenging image sequences show that the proposed method has better performance than the state-of-the-art tracker.

Visual tracking; Sparse representation; Dense representation; Dictionary learning

TP391.4

A

1009-5896(2015)03-0536-07

10.11999/JEIT140507

2014-04-17收到，2014-06-30改回

国家自然科学基金(61175035, 61379105)资助课题

*通信作者：袁广林 yuanguanglin1008@sina.com