基于非局部稀疏编码的超分辨率图像复原

刘 哲 杨 静陈 路

(西北工业大学理学院 西安 710129)

基于非局部稀疏编码的超分辨率图像复原

刘 哲 杨 静*陈 路

(西北工业大学理学院 西安 710129)

基于压缩感知的超分辨率图像复原方法通常采用局部稀疏编码策略，对每一图像块独立编码，易产生人工的分块效应。针对上述问题，该文提出一种基于非局部稀疏编码的超分辨率图像复原方法。该算法在字典训练和图像编码过程中分别运用图像的非局部自相似先验知识，即利用低分辨率图像的插值图像训练字典，并通过计算相似块局部编码的加权平均，得到每一图像块的非局部稀疏编码。仿真实验表明，所提算法能够获得更优的复原效果，并且对于含噪图像具有较强的鲁棒性。

超分辨率图像复原；压缩感知；非局部自相似；非局部稀疏编码；单字典训练

1 引言

随着信息技术的发展，高质量、高清晰度的图像日益成为遥感、医学和生物识别等领域的普遍需求。然而，在图像获取过程中，由于成像系统自身的局限性，所获得的图像往往分辨率较低，无法反映真实场景的信息。因此，图像的超分辨率复原方法被提出并迅速成为国内外学者的研究热点。

压缩感知(Compressive Sensing, CS)[1]理论的发展为超分辨率图像复原提供了新的思路。CS理论指出：在适当条件下，高分辨率(High Resolution, HR)图像可由其下采样产生的低分辨率(Low Resolution, LR)图像以高概率复原[2]。2009年，Sen等人[3]将CS理论应用于超分辨率图像复原，利用HR图像在小波基下可被稀疏编码的先验知识，加入模糊滤波器降低下采样矩阵与小波基间的相关性，并在CS理论框架下求解HR图像。然而由于一般自然图像细节丰富、结构复杂，小波基无法为其提供最优的稀疏编码。文献[4,5]使用随机选取的成对高、低分辨率图像块来稀疏表示图像，提高了复原图像的视觉效果，但为了实现精确重构需要大量成对的图像块构造高、低分辨率字典，计算复杂度高。

为了降低该类算法的计算复杂度，Yang等人[6,7]通过设计退化矩阵，将双字典(高、低分辨率字典)训练改进为单字典训练，仅运用少量HR图像块训练高分辨率字典。文献[8]运用聚类和多任务学习的思想同时训练多个只含少量原子的字典。2013年，Liu等人[9]进一步将图像的形态学分解思想应用于字典训练过程中，运用形态学构成分析方法将训练集图像分解为不同的形态学部分，针对每一部分构造相应的字典，提高了复原图像的质量。

然而，基于压缩感知的复原方法[6]对每一图像块独立编码，未考虑不同图像块之间的联系，使得复原图像存在人工的分块效应和模糊。近年来有关图像冗余的研究成果表明，自然图像具有非局部的自相似性质(Non-local Self-Similarity, NSS)[10]，即图像中存在大量相似的图像块结构，而这些相似块的空间距离可能较远。利用这种图像冗余对相似块进行相关操作，有利于保持图像的边缘，已被广泛应用于求解各类图像处理中的反问题[10-14]。

为了消除复原图像中存在的人工分块效应及模糊，本文基于图像的NSS性质，引入基于NSS的字典训练方法，并通过将相似块的局部编码作加权平均，对每一图像块进行非局部稀疏编码，实现了一种基于非局部稀疏编码的超分辨率图像复原算法。

2 基于压缩感知的超分辨率图像复原

基于压缩感知的超分辨率图像复原方法[6]通过设计退化矩阵，在压缩感知理论框架下求解复原图像，将复杂的双字典训练过程[4,5]改进为单字典训练，算法的时间效率明显提高。

首先，利用随机选取的HR图像块通过K奇异值分解(K-means Singular Value Decomposition, K-SVD)算法训练高分辨率字典Dh[15]。将LR图像Y分块，对每一图像块y，复原旨在求解其相应的HR图像块x，其中y可看作是由x经过退化矩阵H和噪声N作用得到的，即

上述图像退化方程的求解是一个高度不适定的病态反问题，其解并不唯一。CS理论指出，若x在某个与H不相关的过完备字典Dh下可被稀疏编码，即

那么上述不适定问题可转化为求解式(3)所示的优化问题：

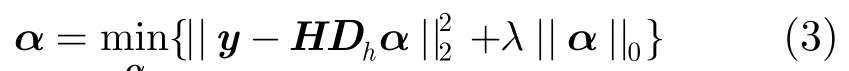
式中α为图像块x的稀疏编码，||α||0＜＜K (||α||0表示α中非零元素的个数，K为α所含元素的总数)，λ为正常数，用于平衡两项约束条件所占的比重。运用基追踪算法求解优化问题式(3)，再由式(2)即可得到HR图像块x，组合HR图像块得到HR图像X。

上述算法充分利用了自然图像的稀疏性质，且只进行单字典训练的思想使得算法的计算复杂度有效下降。然而该方法对每一图像块进行独立复原，忽略了相似图像块的稀疏编码之间的联系，使得复原图像中存在不同程度的人工分块效应，在图像边缘处容易出现锯齿现象。为克服以上不足，本文在上述复原方法的基础上，综合利用图像的局部稀疏与非局部自相似性质进行复原。

3 基于非局部稀疏编码的超分辨率图像复原

3.1 基于NSS的字典训练

图像复原效果的优劣依赖于字典的选择。利用大量随机选取的HR图像块训练成字典来稀疏表示图像，能够充分利用训练集图像所提供的高频信息[4-9]。然而由于HR图像是随机选择的，它们在外观上与待复原的LR图像有较大的差别，因此这些HR图像为复原提供的细节信息可能是不准确的。

由于自然图像具有非局部自相似性，LR图像及其相应的插值图像中相似的图像块结构能够为复原提供必要的细节信息。本文首先利用双三次(Bicubic)和双线性(Bilinear)两种插值算法对LR图像进行插值，再将插值图像作为训练集进行字典训练，这样就充分利用了图像的冗余特性，使得训练出的字典Dh有更强的表现力。双三次与双线性算法是两种常见且简单易行的图像插值算法，由于插值算法不同，其产生的插值图像便能够提供不同的细节信息。使得训练集图像更丰富，得到的字典能更准确地稀疏表示图像。基于NSS的字典训练过程如下：

(1)分别用双三次与双线性插值算法插值LR图像Y，得到训练集图像X1,X2；

(2)将X1,X2分块，组成训练集Qh=[x1x2…xq](其中xi为第i个图像块的向量形式)，记B=[b1b2…bq]为相应的稀疏编码矩阵，利用K-SVD算法求解以下优化问题：

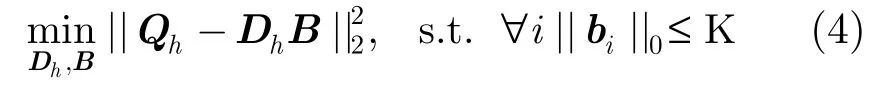
得到高分辨率字典Dh=[d1d2…dK]；

(3)标准化Dh，使得||dj||2=1,j=1,2,…,K。

3.2 非局部稀疏编码

在文献[6]算法框架的基础上，对图像块的局部编码系数作非局部处理。首先对每一图像块xi，用正则化正交匹配追踪(Regularized Orthogonal Matching Pursuit, ROMP)[16]算法求解优化问题式(3)得到其局部稀疏编码αi；之后在整幅图像中搜索图像块xi的相似块xj，并通过式(5)计算xi的非局部稀疏编码βi：

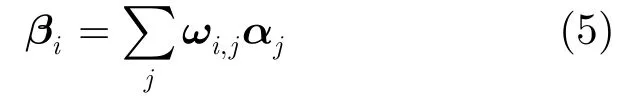
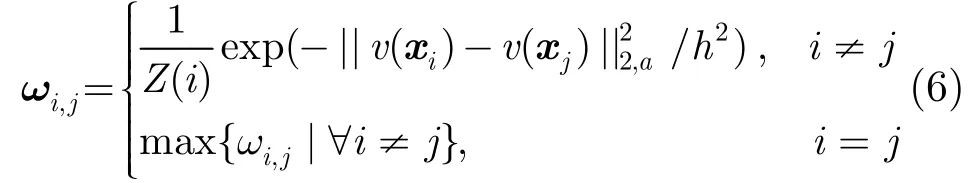
3.3 本文算法步骤

综合以上分析，本文算法流程如图1所示。

具体步骤总结如下：

输入：LR图像Y，放大倍数s，退化矩阵H。

步骤1 用Y的插值图像作为训练集，并利用K-SVD算法训练字典hD；

步骤 2 对每一图像块yi，由ROMP算法求解式(3)，得到其局部稀疏编码；

步骤4 迭代执行以下步骤，更新X(t)得到X(t+1),t=0,1,2,…。

(1)在X(t)中搜索的相似块，并由计算的非局部稀疏编码；

(3)对X(t+1)进行迭代反投影计算，进一步减小误差。

输出：HR图像X。

4 仿真实验及结果分析

为检验本文算法的有效性，对多类图像进行超分辨率复原实验。实验中LR图像块的大小取为22×。为保持复原图像中块与块间的一致性，块与块之间有一个像素的重叠。考虑到人眼对彩色图像的亮度通道较为敏感，只对亮度通道采用上述算法，其余通道利用Bicubic插值算法复原。

为比较不同算法的复原质量，采用峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)和结构化自相似程度(Structural SIMilarity, SSIM)两种客观评价标准。PSNR指标通过计算复原图像与原图像的欧式距离来评价重构质量，计算公式为

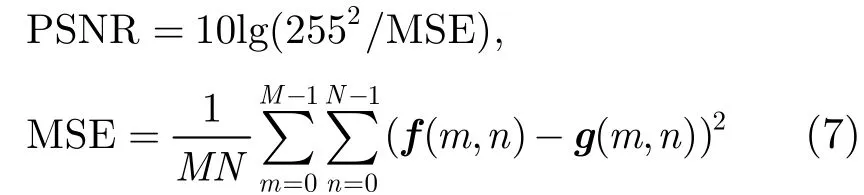
这里(,)mnf,(,)mng分别代表原始图像与复原图像，图像大小为MN×。PSNR值越高，复原图像与原图像越接近，复原质量越好；SSIM指标与人眼的视觉感知系统相关，计算公式为

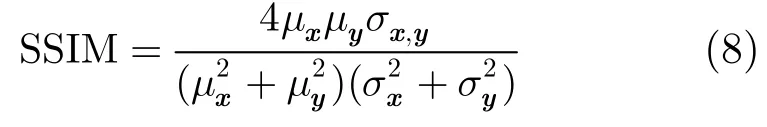
μx,μy表示原始图像与复原图像的均值，σx,σy为图像标准差，σx,y为原始图像与复原图像的协方差。SSIM值介于01～之间，越接近1，说明复原图像与原图像结构化相似程度越高，复原效果越好。

4.1 自然图像实验

为验证本文算法的有效性，对多幅不同类型、不同特点的图像(实验LR图像如图2)进行复原实验，放大倍数为2。将本文算法与双三次插值、基于压缩感知的复原算法[6,7]进行比较，部分实验结果的局部放大图如图3所示，实验图像的PSNR与SSIM指标如表1所示，表中最后一列给出了不同算法下评价指标的平均值。

无论从主观视觉效果还是客观评价指标来看，本文算法都取得了更好的复原效果。由局部放大图可知，双三次插值算法生成的复原图像过于平滑，文献[6]算法图像在边缘处有锯齿效应和模糊，而本文算法具有更加清晰的边缘和细节。由客观评价指标可知，本文算法复原效果略优于文献[7]算法，这是由于本文算法中基于NSS的字典训练方式使用LR图像的插值图像训练字典，更有利于保护图像的细节信息。图表中本文算法1为去掉本文算法中非局部稀疏编码部分(即步骤4(1)，步骤4(2))的实验结果。由本文算法1与本文算法的对比结果可以看出，非局部稀疏编码策略带来了很大的性能提升。这是由于非局部稀疏编码策略充分利用了相似图像块所提供的信息，加强了图像块稀疏编码间的联系，使得每一图像块的编码不再彼此独立。

图1 基于非局部稀疏编码的超分辨率图像复原算法流程图

图2 实验图像

图3 自然图像复原实验结果局部放大图

4.2 含噪图像实验

由于受到环境因素的影响和成像系统自身的局限性，人们所获得的图像往往含有不同程度的噪声。为验证本文算法对噪声的鲁棒性，对含噪图像进行超分辨率复原实验。选取Lena和遥感2105含噪图像进行仿真实验，实验中通过加入均值为0，标准差σ为5, 10, 15的高斯白噪声来模拟实际获取的图像中所含的噪声，复原图像的PSNR与SSIM指标如表2所示。图4为噪声标准差10σ=时的实验结果。

分析图表数据可知，在对含噪图像进行复原时，文献[6]算法的复原结果有时并不如传统的双三次插值算法好，而本文算法的复原效果较优。由于非

局部稀疏编码本质上相当于对图像的稀疏编码系数进行滤波，而滤波过程是图像去噪的重要手段，因此本文算法针对含噪图像具有较强的鲁棒性，能够在放大图像的同时抑制图像中的噪声。这也使得本文算法更加适用于实际应用。

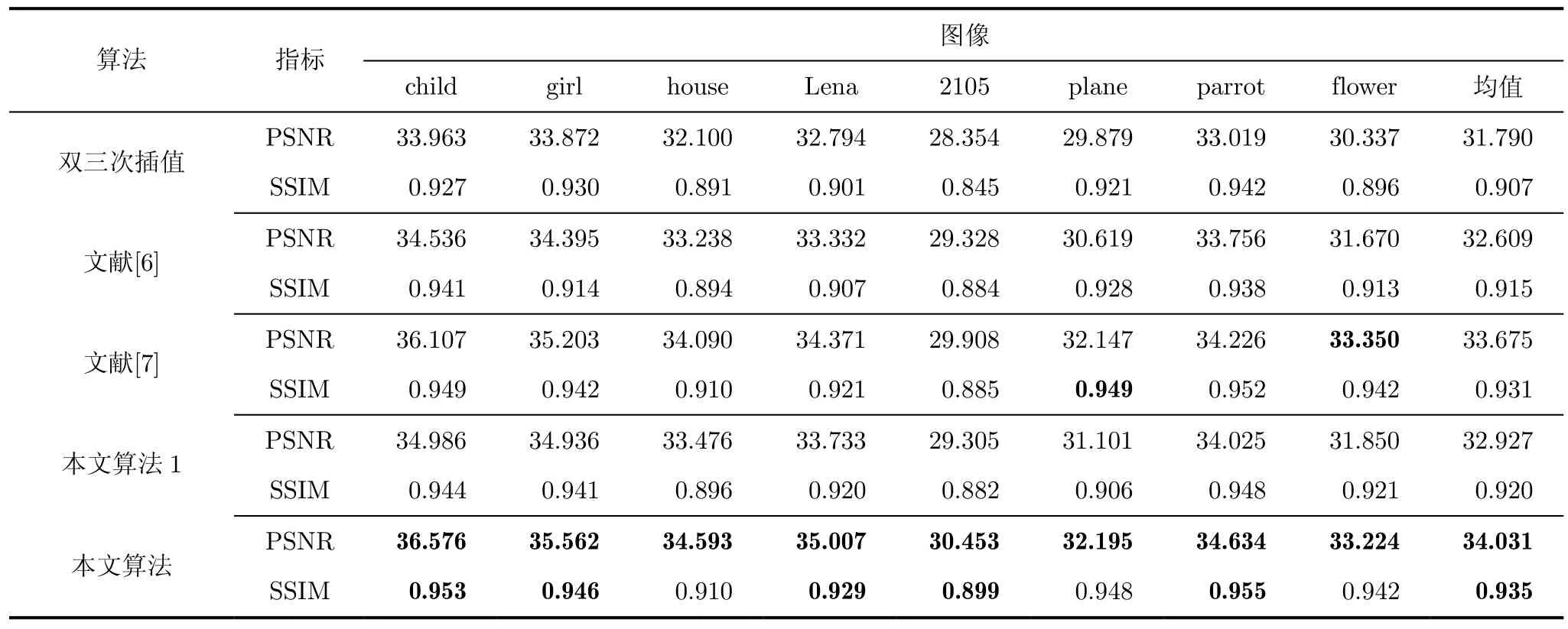
表1 不同算法下自然图像复原结果比较

表2 不同算法下含噪图像复原结果比较

图4 含噪图像复原实验结果

4.3 不同放大倍数下各算法复原效果的比较

超分辨率图像复原要求复原算法能够对低分辨率图像进行不同倍数的放大，放大倍数越高，复原所需添加的细节信息就越多，复原工作越复杂。实验选取9696×的Child图像，分别用双三次插值、文献[6]算法和本文算法对其进行1.5, 2.0, 2.5, 3.0, 4.0, 5.0倍放大，并对实验结果描点绘图，如图5所示。由曲线变化图可知，随着放大倍数的增加，复原效果逐渐变差。放大5.0倍时，文献[6]算法相比于双三次插值算法效果较差，而本文算法却能取得较好的复原效果。这是由于稀疏编码理论能够从少量的采样值中抓住图像的关键信息进行图像复原，并且本文算法充分利用了图像的非局部自相似先验知识。

5 结束语

压缩感知与稀疏编码理论可实现低维信号到高维信号的精确重构，基于稀疏编码的超分辨率图像复原方法也成为近年来的研究热点[17,18]。本文在此基础之上，将图像的非局部自相似性质作为先验知识，在训练字典和图像编码过程中分别运用这一先验知识，提出了一种基于非局部稀疏编码的超分辨率图像复原方法，并进行了仿真和对比实验。实验结果验证了算法的有效性和鲁棒性。在非局部稀疏编码的过程中，图像块的相似度判断起着关键作用。本文采用欧式距离判断相似程度，其优点是简单易行，但也存在不能反映块结构特点的不足。在未来的工作中，设计更加有效的相似块评判标准、结合更多的图像先验知识进行复原，是值得进一步研究的问题。

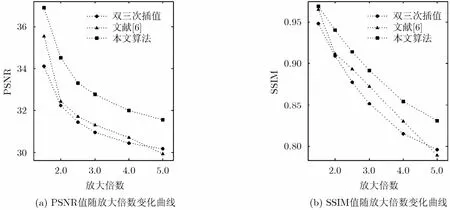
图5 不同算法下评价指标随放大倍数变化曲线图

[1] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[2] Kulkarni N, Nagesh P, Gowda R, et al.. Understanding compressive sensing and sparse representation-based super-resolution[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(5): 778-789.

[3] Sen P and Darabi S. Compressive image super-resolution[C]. 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, 2009: 1235-1242.

[4] Yang J, Wright J, Huang T S, et al.. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.

[5] Lu J, Zhang Q, Xu Z, et al.. Image super-resolution by dictionary concatenation and sparse representation with approximate L0norm minimization[J]. Computers & Electrical Engineering, 2012, 38(5): 1336-1345.

[6] Yang S, Sun F, Wang M, et al.. Novel super resolution restoration of remote sensing images based on compressive sensing and example patches-aided dictionary learning[C]. 2011 International Workshop on Multi-Platform/Multi-Sensor Remote Sensing and Mapping (M2RSM), Xiamen, 2011: 1-6.

[7] Yang S, Wang M, Sun Y, et al.. Compressive sampling based single-image super-resolution reconstruction by dual-sparsity and non-local similarity regularizer[J]. Pattern Recognition Letters, 2012, 33(9): 1049-1059.

[8] Yang S, Liu Z, Wang M, et al.. Multitask dictionary learning and sparse representation based single-image super-resolution reconstruction[J]. Neurocomputing, 2011, 74(17): 3193-3203.

[9] Liu W and Li S. Multi-morphology image super-resolution via sparse representation[J]. Neurocomputing, 2013, 120(23): 645-654.

[10] Buades A, Coll B, and Morel J M. A review of image denoising algorithms, with a new one[J]. Multiscale Modeling & Simulation, 2005, 4(2): 490-530.

[11] Yu H, Chen F, Zhang Z, et al.. Single infrared image super-resolution combining non-local means with kernel regression[J]. Infrared Physics & Technology, 2013, 61: 50-59.

[12] Dong W, Zhang D, Shi G, et al.. Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization[J]. IEEE Transactions on Image Processing, 2011, 20(7): 1838-1857.

[13] Romano Y, Protter M, and Elad M. Single image interpolation via adaptive non-local sparsity-based modeling[J]. IEEE Transactions on Image Processing, 2014, 23(7): 3085-3098.

[14] Dong W, Shi G, Zhang L, et al.. Super-resolution with nonlocal regularized sparse representation[C]. Visual Communications and Image Processing 2010, Huangshan, China, 2010: 77440H-77440H-10.

[15] Aharon M, Elad M, and Bruckstein A. K-svd: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[16] Needell D and Vershynin R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit[J]. Foundations of Computational Mathematics, 2009, 9(3): 317-334.

[17] Yang S, Wang M, Chen Y, et al.. Single-image superresolution reconstruction via learned geometric dictionaries and clustered sparse coding[J]. IEEE Transactions on Image Processing, 2012, 21(9): 4016-4028.

[18] Tang Y, Yuan Y, Yan P, et al.. Greedy regression in sparse coding space for single-image super-resolution[J]. Journal of Visual Communication and Image Representation, 2013, 24(2): 148-159.

刘 哲： 女，1970年生，教授，博士，主要研究方向为图像处理、压缩感知和信息融合等.

杨 静： 女，1990年生，硕士生，研究方向为图像复原、压缩感知.

陈 路： 男，1991年生，硕士生，研究方向为图像去块效应、图像处理.

Super-resolution Image Restoration Based on Nonlocal Sparse Coding

Liu Zhe Yang Jing Chen Lu

(School of Science, Northwestern Polytechnical University, Xi’an 710129, China)

Super-resolution image restoration methods based on Compressive Sensing (CS) generally adopt local sparse coding strategy. Such strategy encodes each image block independently, which easily induces artificial blocking effect. To overcome this problem, a super-resolution image restoration method based on nonlocal sparse coding is proposed. The nonlocal self-similarity of image is considered as a prior in the dictionary training and image coding processes, respectively. Specifically, the proposed algorithm trains the dictionary with interpolated low-resolution images, and calculates the weighted average local code of similar patches, in order to obtain the nonlocal sparse code of each image block. Numerical experiments suggest that the proposed algorithm has a good recovery performance, and is robust to image noise.

Super-resolution image restoration; Compressive Sensing (CS); Nonlocal self-similarity; Nonlocal sparse coding; Single dictionary training

TP391

A

1009-5896(2015)03-0522-07

10.11999/JEIT140481

2014-04-11收到，2014-09-11改回

国家自然科学基金(61070138)资助课题

*通信作者：杨静 yangjing199002@163.com