评估交换超立方体网络可靠性的一种新方法

梁家荣白 杨王新阳

①(广西大学计算机与电子信息学院 南宁 530004)

②(华南理工大学计算机科学与工程学院 广州 510006)

评估交换超立方体网络可靠性的一种新方法

梁家荣*①白 杨①王新阳②

①(广西大学计算机与电子信息学院 南宁 530004)

②(华南理工大学计算机科学与工程学院 广州 510006)

交换超立方体互连网络(EH(s,t))作为大规模处理器系统网络模型的重要候选之一，其可靠性问题一直为人们所关注。该文利用额外连通度作为评价可靠性的重要度量，对交换超立方体互连网络的可靠性进行分析，得到了交换超立方体网络的2-额外点连通度(k2(EH(s,t)))和2-额外边连通度(λ2(EH(s,t )))，证明了当t≥s≥2时，k2(EH(s,t))=3s-2；当t≥s≥3时，λ2(EH(s,t))=3s-1。分析说明了对交换超立方体互连网络的可靠性评价时，2-额外连通度较之传统连通度更具有优势性。

互连网络；交换超立方体；可靠性；额外连通度

1 引言

互连网络的可靠性主要是指在网络的部分节点、部分链路出现故障时，剩余子网是否仍能保持正常通信的能力。随着网络规模的不断扩大，网络中出现故障节点、故障链路的情况不可避免，因此网络的可靠性问题就成为不可回避的研究课题。其中，点连通度和边连通度是衡量网络可靠性的两个重要参数，它们表明了一个网络能容忍同时故障的最大节点数和最大链路数。但点连通度和边连通度在衡量网络可靠性方面也存在不足的地方：它们都默认一个节点或一条链路的所有邻居节点(或邻居链路)可能同时出现故障，而这种情况在实际的网络中几乎不可能存在，例如在一个具有2n个节点的正则度为n的规则互连网络中，一个节点的所有邻居点同时故障的概率是2n/＜10-6(当n≥6时)，这种概率的事件几乎不可能发生，因此用点连通度和边连通度研究互连网络的可靠性不切实际。

为了解决这一问题，Haray在传统连通度的基础上加入一些限制条件，提出了条件连通度[1]的概念。后来，Fabrega和Fiol将这一限制条件进一步细化提出了额外连通度的概念[2,3]。额外连通度一经提出便引起众多学者的高度关注，并获得众多研究成果[4-10]。文献[4]研究了超立方体[11]的2-额外连通度；文献[5]将超立方体的额外连通度精确到了h阶，这极大提升了超立方体网络的可靠性精度；文献[6]从网络中不存在孤立节点、孤立链路的角度分别研究了折叠超立方体网络[12]的2-额外点连通度和2-额外边连通度；文献[9]研究了一类特殊正则网络的2-额外连通度；文献[10]则将该类特殊正则网络的可靠性精度提升到h阶，证明了当0≤h≤n-4时，n维一一对应连接(Bijection Connected,BC)网络[13]的h-额外连通度是n(h+1)-(h(h+3))/2，这为进一步研究更大规模的具有失效节点的BC互连网络的可靠性提供了支持。

在众多互连网络结构中，超立方体是最具吸引力的网络之一，但它并非各方面性质最好的。针对超立方体的一些缺陷，不少学者提出了很多超立方体的变种[12,14-17]。作为其中最重要的网络之一，交换超立方体[17]不仅保持了超立方体大量的优秀属性，并且拥有比超立方体更好的属性，如其边数几乎是超立方体边数的一半。目前，关于交换超立方体互连网络的研究已经有很多成果[18-21]，其中可靠性问题备受人们关注。文献[18]证明了交换超立方体的点连通度和边连通度均为1s+；在文献[19]中，Ma等人从网络中不存在孤立节点的角度证明了交换超立方体网络的超点连通度和超边连通度均为2s，这将交换超立方体网络的可靠性的精度提升了近2倍。尽管如此，但上述参数仍有一定缺陷，例如当n很大时，交换超立方体的连通度1s+和超连通度2s与节点总数2s+t+1的比值均非常小，以至于失去了实际意义，而额外连通度在一定程度上克服了这一缺陷。因此用额外连通度来研究交换超立方体的可靠性具有较高的学术意义和应用价值。本文主要在传统连通度和超连通度的基础上，深入剖析了交换超立方体网络的2-额外点连通度和2-额外边连通度，证明了当t≥s≥2时，k2(EH(s,t))=3s-2；当t≥s≥3时，λ2(EH(s,t))=3s-1。最后，分析说明了在评价交换超立方体互连网络的可靠性时，2-额外连通度比传统连通度更精确、更符合实际情况。

2 预备知识

本文中没有定义的理论术语与符号描述，本文将参照文献[22]中的相关定义。在无向图G中，V(G), E(G)分别表示图G的顶点集和边集。对于图G中的任意的集合F，令G-F表示图G在移除了F中所有元素之后所形成的子图。|S|表示集合S的基。(u,v)∈E(G)表示G中任意一条边。NG(u)和EG(u)分别表示顶点u的邻居结点集和邻居边集，且NG(u)={v∈V(G)|∀(u,v)∈E(G)}, EG(u)={(u,v)∈E(G)|∀v∈V(G)}。NG(P)和EG(P)分别表示路径P在图G中的邻居结点集和邻居边集，且NG(P)=(∪∀u∈V(P)NG(u))-V(P),EG(P)=(∪u∈V(P)⋅EG(u))-E(P)。

定义1[17]交换超立方体被定义为一个无向图EH(s,t)=(V,E)(s≥1,t≥1)。顶点集V={as-1…a0bt-1…b0c|ai,bj∈{0,1}且i∈[0,s),j∈[0,t)}。该类超立方体包含3种类型的边E1, E2和E3，描述为

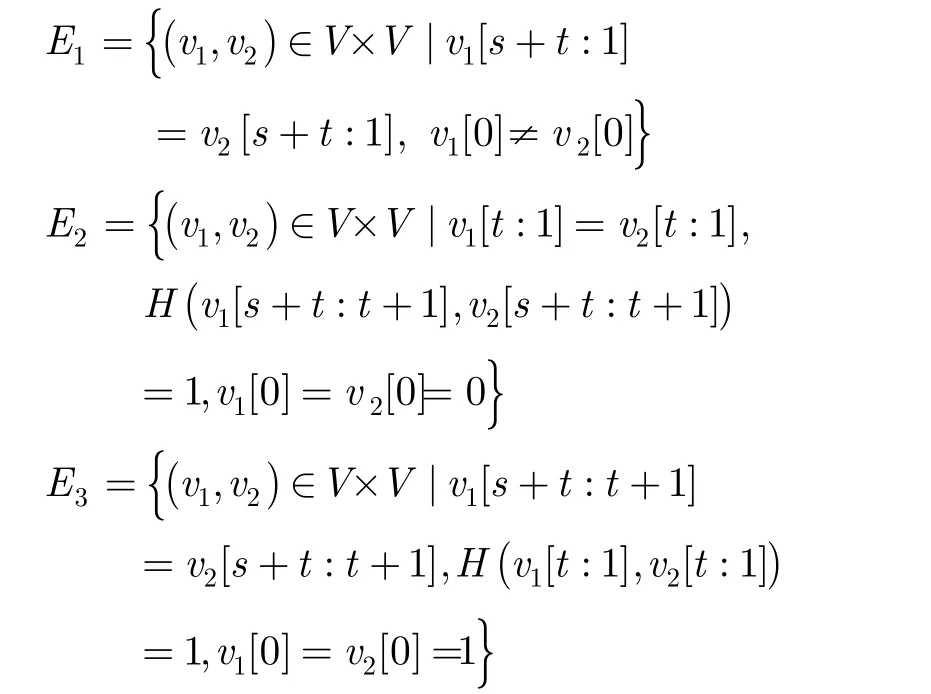
其中v[x:y]表示v的第y位与第x位之间的比特串，H(v1,v2)表示顶点v1,v2之间的海明距离。图1示出了两个交换超立方体EH(1,1)和EH(1,2)。

引理 1[17]EH(,)st同构于EH(,)ts。

引理 2[17]EH(,)st可分解为同构于EH(1,)st-或EH(,1)st-的两个子图。

根据引理1，本文只讨论当st≤时EH(,)st的情况，为了研究需要，将EH(,)st分解成子图L和R，其中

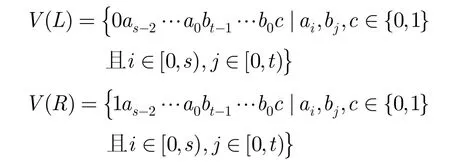
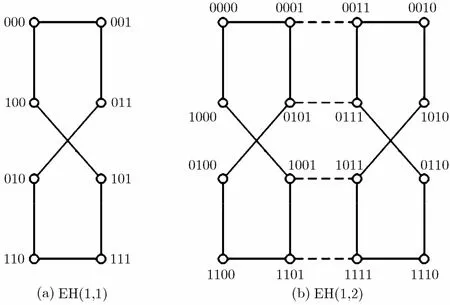
图1 两个交换超立方体EH(1,1)和EH(1,2)

由定义1可知，EH(,)st是在超立方体的基础上通过系统地移除部分边而得到。因此，它是超立方体的一个生成子图，保留了其大量优越属性。

引理 3 在EH(,)st中，任意两个不相邻顶点的公共邻居最多是2。

定理 1 若P为EH(,)st中任意一条长度为2的路，则NEH(s,t)(P)≥3s-2。

证明 由定义1及引理3，很容易证明NEH(s,t)(P)≥3s-2。 证毕

定理 2 若P为EH(s,t)中任意一条长度为2的路，则EEH(s,t)(P)≥3s-1。

证明 由定义1中边的特性，很容易证明EEH(s,t)(P)≥3s-1。 证毕

3 交换超立方网络的额外连通度

3.1 删除部分结点(边)的stEH(,)的连通性

在交换超立方网络的运行中，出现故障结点和失效链路是不可避免的，存在故障结点和失效链路的交换超立方网络仍能保持通信是网络分析中重要考虑的问题之一。下面本文考虑删除部分结点(边)后，交换超立方网络的连通性问题。

定理 3 对于任意的F⊆V(EH(s,t ))且|F|≤3s-3，令Fl=F∩V(L), Fr=F∩V(R)。若在EH(s, t)-F中既无孤立顶点也无孤立边，则R-Fr(或L-Fl)中每一个顶点均与L-Fl(或R-Fr)中一个顶点连接。

证明 对于任意的顶点ur∈V(R-Fr), ur= 1as-2…a0bt-1…b0c ，分以下两种情形进行讨论。

(1)令ur=1as-2…a0bt-1…b00。若ul=0as-2…a0bt-1…b00∉F ，则定理得证。否则ul∈F。如果存在ur0=1as-2…a0bt-1…b01∉F ,1as-2…a0bt-1…且，那么从ur出发总存在一条路径使其连接至L-Fl，定理得证。否则ur0∈F。如果且uri(s+t)=0as-2，则定理得证。否则uri与 uri(s+t)(0≤i≤s -2)中至少一个顶点在F中，此时令A={uri,uri(s+t)|0≤i≤s-2}∩F ，则必有|A|≥s-1。

因为EH(s,t)-F中不存在孤立点，不妨令vr=，如此(ur,vr)∈E(R-Fr)。若，则定理得证。否则vl∈F。如果存在且b00∉F，那么从ur出发经过vr，总存在一条路径使其连接至L-Fl。 否则vr0∈F。如果vrj=1as-2…且，则定理得证。否则其中之一必在F中，此时令B={vrj,vrj(s+t)|0≤j≤s-2且j≠i}∩F，则|B|≥s-2。

令C={wrk,wrk(s+t)|0≤k≤s-2,k≠i,j }, D= {ul,vl,wl,ur0,vr0,wr0}，其中wl∈F, wr0∈F。由于而在C中有s-3对顶点使ur连接至L-Fl，因此至少存在一个常数k(k≠i,j)使u与L-Fl中一个顶点相连接，定理得证。

(2)令ur=1as-2…a0bt-1…b01。由于N(ur)∩V(L) =φ若，则存在一条路径，使ur连通至L-Fl。否则u′∈F。令，若|A′|＜t，则必定存在某一i′使1as-2…a0bt-1…bi′…b01b00∉F，如此ur连通至L-Fl。否则|A′|≥t。因为EH(,)stF-中不存在孤立点，不妨令，如此(ur,)∈E(EH(s,t)-F)。若，则ur连通至L-Fl。否则v′∈F。令j′≤t-1,j′≠i′}∩F ，若|B′|＜t-1，同理可得ur连通至L-Fl。否则，令|B′|≥t-1。

…bi′…bj′…b0；或w′→1a…ab…bi′…bj′

0

轻量级、大众化 原生应用是专门针对某一类移动设备而开发的，下载并安装到设备里进行使用；轻量级应用是指基于微信等应用软件，以一定形式为用户提供的应用服务，具有上手容易、发展迅速的特点[3]。教师采用轻量级形式的全民学习共享平台，花费更多心思在教学设计上，深耕教学内容，打磨出高品质的智慧课堂。教师可以零成本地开发课程资源，对制作好的PPT添加语音讲解，引入学生投票、提问、评论功能，促使学生更加专注。教师可以登录微信完成课件的移动查阅、实时推送，可以通过雨课堂或微信群的形式建立立体交流、互动互助的共享空间，又能实现点对点的个人交流空间。

令C′={u′,v′}，由于|F-(A′∪B′∪C′)|≤(3s-3)-t-(t-1)-2≤s -4，而ur通过可构造t-1条路径且t-1≥s-1＞s-4，如此至少存在一条路径使ur与L-Fl中的一个顶点相连接，定理得证。

定理4 对于任意的F′⊆E(EH(s,t ))且|F′|≤3s -2，令=F′∩E(L),=F′∩E(R),=F′∩M0。若在EH(s,t)-F′中既无孤立顶点也无孤立边，则中每一个顶点均与中一个顶点相连。

证明 设ur为R-F中任意一顶点，令ur= 1as-2…a0bt-1…b00，则有以下两种情形。

(1)令ur=1as-2…a0bt-1…b00。 若es+t(ur)= (ul,ur)∉F′，则定理得证。否则es+t(ur)∈F′。若且∉F′，则存在一条路径使ur连通至L-，定理得证。否则e0(ur)∈F′。令A={ei(ur),es+t(uri)|0≤i≤s-2}∩F′，若|A|＜s-1，则必定存在某一i，使ei(ur)∉F′且es+t(uri)∉F′，如此ur必定与L-中某一顶点相连接，定理得证。否则|A|≥s-1。

由于EH(s,t)-F′中无孤立顶点，如此存在某一ei(ur)∉F′使(ur,uri)∈E(EH(s,t)-F′)。若es+t(uri)∉F′，则定理得证。否则es+t(uri)∈F′。若e0(uri)∉F′，此时可以形成一条通向L-Fl′的路径为：

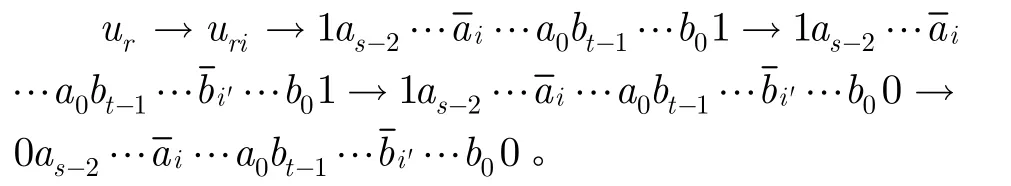
如此定理可证。否则e0(uri)∈F′。令B={ej(uri), es+t(urij)|0≤j≤s-2,j≠i}∩F′，若|B|＜s-2，则必定存在某一j，使ej(uri)∉F′,es+t(urij)∉F′, ur可通过一条路径连接至L-，定理可证。否则|B|≥s-2。

由于EH(s,t)-F′中不存在孤立边，因此存在ej(uri)∉F′且j≠i，如此ur经过urij至L-可构造如下路径：

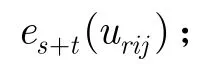
或ek(urij)→es+t(urijk)，其中0≤k≤s-2且 k≠i,j。

令C={es+t(ur),e0(ur),es+t(uri),e0(uri)}，因为|F′-A∪B∪C|=|F′|-|A|-|B|-|C|≤(3s -2) -(s-1)-(s-2)-4=s-3，而ur通过urij可构造(s-1)条通向L-的路径，如此至少存在一条路径使ur与L-中一个顶点相连，定理得证。

(2) 令ur=1as-2…a0bt-1…b01。 由于N(ur)∩V(L)=φ，若e0(ur)F′，则此时存在一条路径ur→ur0→0as-2…a0bt-1…b00，定理得证。否则e0(ur)∈F′。令≤t-1}∩F′，若|A′|＜t，则同理可得存在某一i′，使，如此ur可连接至L-Fl′中一个顶点，定理可证。否则|A′|≥t。

，同理通过uri′j′可构造通向的路径为：

uri′j′→，其中0≤k′≤t-1且k′≠i′,j′。

令C′={e0(ur),e0(uri′)}，由于|F′-A′∪B′∪C′|≤(3s-2)-t-(t-1)-2≤s -3,而ur通过uri′j′可构造(t-1)条通向L-的路径，其中t≥s，因此至少存在一条路径使ur与L-中一个顶点相连，定理得证。

3.2 stEH(,)的2-额外连通度

额外连通度是评价交换超立方网络可靠性的重要度量，依靠于3.1节的结论，下面给出交换超立方网络的2-额外连通度的相关结果。

引理 4[19]当s≤t时，k′(EH(s,t))=λ′(EH(s,t)) =2s。定理 5 k2(EH(s,t))=3s-2，其中t≥s≥2。证明 在EH(s,t)中任取一条长度为2的路径P，由定理1有NEH(s,t)(P)≥3s-2。很容易验证，EH(s,t)-NEH(s,t)(P)既不包含孤立顶点，也不包含孤立边，如此NEH(s,t)(P)为一点割集且k2(EH(s,t))≤3s-2。若要证明定理5成立，只需证明k2(EH(s,t))≥3s-2，即证明对于任意的顶点集F⊆V(EH(s,t))，当|F|=3s-3且不存在孤立顶点也不存在孤立边时，EH(s,t)-F是连通的。令Fl=F∩V(L), Fr=F∩V(R)，由定理3可知，R-Fr中任意一顶点与L-Fl中一顶点连通。如此，只需证明当|F|=3s-3且在EH(s,t)-F不存在孤立顶点也不存在孤立边时，L-Fl是连通的即可。不失一般性，令|Fl|≤|Fr|，则|Fl|≤(3s-3) /2＜2s-2(s≥2)。

若在L-Fl中无孤立点，而|Fl|＜2s-2= k′(L)，则L-Fl是连通的，定理得证。否则在L-Fl中有孤立点，假设有两个孤立点，记为x,y。由于|NL(x)|,|NL(y)|≥(s-1)+1=s ，且在L中任意两个不相邻顶点之间的公共邻居最多为2，故至少移出(2s-2)个顶点才能得到两个孤立点，而|Fl|＜2s-2，如此在L中只存在一个孤立点，设为ul，即NL(ul)⊆Fl且|NL(ul)|≥s。下面证明当|F|=3s-3且在EH(s,t)-F不存在孤立顶点也不存在孤立边时，ul与L-Fl∪{ul}是连通的。

若 ul=0as-2…a0bt-1…b01时，由于N(ul)∩V(R) =φ，则ul在EH(s,t)-F中为一孤立点，这与EH(s,t)-F不存在孤立顶点相矛盾，此时ul只能取下面的值，即 ul=0as-2…a0bt-1…b00。

因为在EH(s,t)-F中无孤立点，故存在ur= 1as-2…a0bt-1…b00∉F ，如此(ul,ur)∈E(EH(s,t ) -F)。若ur0=1as-2…a0bt-1…b01∉F , 1as-2…a0bt-10as-2…a0bt-1…bi′…b00∉F ，则定理得证。否则且则定理得证。否则令A={uri,uri(s+t)|0≤i≤s-2}∩F，则|A|≥s-1。

因为在EH(s,t)-F中无孤立边，如此存在一个uriF，使(ur,uri)∈E(EH(s,t)-F)，则ul通过uri构造通向L-ul的路径为：

uri→，其中0≤j≤ s-2且j≠i。

由于|F-NL(ul)∪A∪{ur0}|≤(3s-3)-s-(s -1)-1=s-3且ul通过uri可构造(s-2)+1= s-1条通向L-ul的路径，故至少存在一条路径使ul与L-Fl∪{ul}连通，定理得证。

引理5[22]对任意的图G，都有k(G)≤λ(G)≤δ(G)。

引理 6[18]当s≤t时，k(EH(s,t))=λ(EH(s,t)) =s +1。

定理 6 λ2(EH(s,t))=3s -1，其中t≥s≥3。

证明 在EH(s,t)中任取一条长度为2的路径P，根据定理2有|EEH(s,t)(P)|≥3s-1。由于EH(s,t)- EEH(s,t)(P)既不包含孤立顶点也不包含孤立边，根据λ2的定义，有λ2(EH(s,t))≤3s-1。如此，只需证明λ2(EH(s,t))≥3s-1，即证明对于任意的边集F′⊆E(EH(s,t ))，若|F′|=3s-2且既无孤立顶点也无孤立边时，EH(s,t)-F′为连通的。令=F∩E(L),=F∩E(R),=F∩M0。由定理4可知，R-中每个顶点至少与L-中一个顶点相连接，故只需证明当|F′|=3s-2且EH(s,t)-F′既无孤立顶点也无孤立边时，L-是连通的即可。由于|F′|=3s-2＜4(s -1)(s≥3)，故中至少两个小于2(s-1)，不妨设||＜ 2(s-1)。若L-中无孤立点，且||＜2(s-1) =λ′(L) ，如此L-为连通的，定理得证。否则存在孤立点。同理定理5可得，L-中没有两个孤立点，只能有一个孤立点，记为ul，此时有EL(ul)⊆且|EL(ul)|≥s。由于λ(L-ul)≥k(L而＜s-2＜s -1，如此为连通的。下面只需证明当|F′|=3s-2且在EH(s,t)-F′中既不包含孤立点也不包含孤立边时，ul与L-∪{ul}连通即可。

若ul=0as-2…a0bt-1…b01，由于ul在L-中为孤立点且N(ul)∩V(R)=φ，这与E(EH(s,t)-F′)中无孤立顶点相矛盾，如此ul只能为下面值，即ul=0as-2…a0bt-1…b00。

由于EH(s,t)-F′中无孤立点，如此es+t(ul)∉F′，使(ul,ur)∈E(EH(s,t)-F′)，其中us+t=ur。若e0(ur)∉F′，则ul可通过下面路径连接至L-∪{ul}：

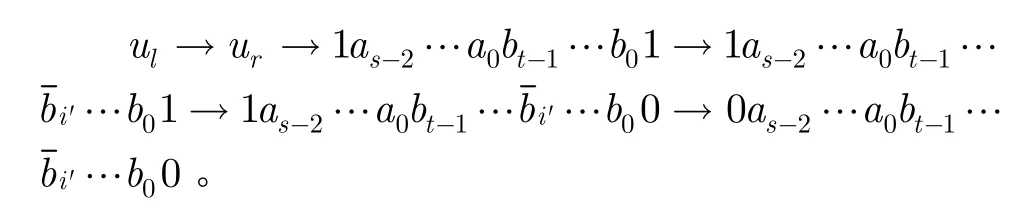
如此，则定理成立。否则e0(ur)∈F′，令A′= {ei(ur),es+t(uri)|0≤i≤s-2}∩F′，则|A′|≥s-1。

由于EH(s,t)-F′中无孤立边，则存在某个i，使ei(ur)F′，如此(ur,uri)∈E(EH(s,t)-F′)，则从ul出发经过uri可构造通向L-ul的路径为：

ul→ur→uri→或ul→ ur→其中0≤j≤s -2且j≠i。

由于|F′-A′∪EL(ul)∪{e0(ur)}|=|F′|-|A′| -|EL(ul)|-1≤s -2，而ul通过uri连接至L-ul的路径有1s-条，故至少存在一条路径使lu连接至

4 stEH(,)的2-额外连通度与传统连通度比较

综上所述，当t≥s≥2时，EH(s,t)的2-额外点连通度是3s-2；当t≥s≥3时，EH(s,t)的2-额外边连通度是3s-1。而当t≥s时，EH(s,t)的传统点连通度和传统边连通度均是s+1。由此可以看出，2-额外连通度几乎是传统连通度的3倍，这使得交换超立方体网络可靠性的量度更加精确，因此2-额外连通度比传统连通度更适合评价大规模交换超立方体网络的可靠性。另一方面，传统连通度假定交换超立方体网络的任一节点或任一链路的所有邻居节点(或邻居链路)都可能同时故障，这种情况发生的概率是2n/＜10-6(当n≥6时)，不切实际。而2-额外连通度假定交换超立方体网络的任一节点或任一链路的部分邻居节点(或邻居链路)不能同时故障，这更符合实际情况，因此在评价交换超立方体互连网络的可靠性时，2-额外连通度比传统连通度更具优势性。

5 结束语

本文在交换超立方体网络传统连通度和超连通度的基础上深入研究，进一步证明了2-额外点连通度和2-额外边连通度：当t≥s≥2时，k2(EH(s,t))= 3s-2；当t≥s≥3时，λ2(EH(s,t))=3s -1。也就是说，当t≥s≥2(或t≥s≥3)时，交换超立方体至少删除3s-2个顶点(或3s-1条边)，才能得到既不包含孤立顶点也不包含孤立边的非连通图。该结果的得出进一步扩展了交换超立方体网络的可靠性研究，同时对交换超立方体网络的可靠性提供了更精确的量度。

[1] Harary F. Conditional connectivity[J]. Networks, 1983, 13(3): 347-357.

[2] Fàbrega J and Fiol M A. Extraconnectivity of graphs with large girth[J]. Discrete Mathematics, 1994, 127(1): 163-170.

[3] Fàbrega J and Fiol M A. On the extraconnectivity of graphs[J]. Discrete Mathematics, 1996, 155(1): 49-57.

[4] Xu J M and Zhu Q. On restricted connectivity and extra-connectivity of hypercubes and folded hypercubes[J]. Journal of Shanghai Jiaotong University, 2005, 10(2): 203-207.

[5] Yang W and Meng J. Extraconnectivity of hypercubes[J]. Applied Mathematics Letters, 2009, 22(6): 887-891.

[6] Zhu Q, Xu J M, Hou X, et al.. On reliability of the folded hypercubes[J]. Information Sciences, 2007, 177(8): 1782-1788.

[7] Hong W S and Hsieh S Y. Extra edge connectivity of hypercube-like networks[J]. International Journal of Parallel, Emergent and Distributed Systems, 2013, 28(2): 123-133.

[8] Li H and Yang W. Bounding the size of the subgraph induced by m vertices and extra edge-connectivity of hypercubes[J]. Discrete Applied Mathematics, 2013, 161(16/17): 2753-2757. [9] Xu J M, Zhu Q, and Xu M. Fault-tolerant analysis of a class of networks[J]. Information Processing Letters, 2007, 103(6): 222-226.

[10] Zhu Q, Wang X K, and Cheng G. Reliability evaluation of BC networks[J]. IEEE Transactions on Computers, 2013, 62(11): 2337-2340.

[11] Saad Y and Schultz M H. Topological properties of hypercubes[J]. IEEE Transactions on Computers, 1988, 37(7): 867-872.

[12] El-Amawy A and Latifi S. Properties and performance of folded hypercubes[J]. IEEE Transactions on Parallel and Distributed Systems, 1991, 2(1): 31-42.

[13] Fan J X. BC interconnection networks and their properties[J]. Chinese Journal of Computers-Chinese Edition, 2003, 26(1): 84-90.

[14] Cheng B, Fan J, Jia X, et al.. Parallel construction of independent spanning trees and an application in diagnosis on Möbius cubes[J]. Journal of Supercomputing, 2013, 65(3): 1279-1301.

[15] Chen J C, Lai C J, Tsai C H, et al.. A lower bound on the number of Hamiltonian cycles through a prescribed edge in acrossed cube[J]. Applied Mathematics and Computation, 2013, 219(19): 9885-9892.

[16] Yang X F, Evans D J, and Megson G M. The locally twisted cubes[J]. International Journal of Computer Mathematics, 2005, 82(4): 401-413.

[17] Loh P K K, Hsu W J, and Pan Y. The exchanged hypercube[J]. IEEE Transactions on Parallel and Distributed Systems, 2005, 16(9): 866-874.

[18] Ma M J. The connectivity of exchanged hypercubes[J]. Discrete Mathematics, Algorithms and Applications, 2010, 2(2): 213-220.

[19] Ma M J and Zhu L Y. The super connectivity of exchanged hypercubes[J]. Information Processing Letters, 2011, 111(8): 360-364.

[20] Li X J and Xu J M. Generalized measures of fault tolerance in exchanged hypercubes[J]. Information Processing Letters, 2013, 113(14): 533-537.

[21] zar Klav∨S and Ma M J. The domination number of exchanged hypercubes[J]. Information Processing Letters, 2014, 114(4): 159-162.

[22] Bondy J A and Murty U S R. Graph Theory with Applications[M]. London: MacMillan, 1976: 10-24.

梁家荣： 男，1966年生，教授，博士，博士生导师，研究方向为网络与并行计算、人工智能.

白 杨： 男，1987年生，硕士生，研究方向为网络与并行计算.

王新阳： 男，1985年生，博士生，研究方向为网络与并行计算、云计算、大数据.

A New Method Used for Evaluating Reliability of the Exchanged Hypercube Network

Liang Jia-rong①Bai Yang①Wang Xin-yang②

①(School of Computer and Electronic Information, Guangxi University, Nanning 530004, China)
②(School of Computer Science & Engineering, South China University of Technology, Guangzhou 510006, China)

Reliability problems on Exchanged Hypercube interconnection network(EH(s,t)) regard as one of important candidates of network models in large-scale processor systems are concerned by people. The extra connectivity, which is an important measure in evaluating the reliability, is utilized to analyze the reliability of exchanged hypercube interconnection network. Then the 2-extra vertex connectivity(k2(EH(s,t)))and 2-extra edge connectivity(λ2(EH(s,t )))of exchanged hypercube interconnection network are obtained. The conclusions are thatk2(EH(s,t))=3s-2 fort≥s≥2; andλ2(EH(s,t))=3s -1 fort≥s≥3. The analysis shows that the 2-extra connectivity is much superior to the traditional connectivity in evaluating the reliability of exchanged hypercube interconnection network.

Interconnection network; Exchanged hypercube; Reliability; Extra connectivity

TP393

A

1009-5896(2015)03-0693-07

10.11999/JEIT140557

2014-04-28收到，2014-07-14改回

国家自然科学基金(61363002)资助课题

*通信作者：梁家荣 gxuliangjr@163.com