基于相关准则的稀疏微波成像方位向采样优化方法

蒋成龙赵 曜张 柘③张冰尘洪 文

①(微波成像技术国家重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院大学 北京 100190)

基于相关准则的稀疏微波成像方位向采样优化方法

蒋成龙*①②③赵 曜①②张 柘①②③张冰尘①②洪 文①②

①(微波成像技术国家重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院大学 北京 100190)

稀疏微波成像将稀疏信号处理理论系统性地引入微波成像中，与传统合成孔径雷达成像相比，具有提高成像质量、降低系统复杂度等优点。稀疏采样方式是影响稀疏微波成像重建质量的重要因素。该文主要研究方位向稀疏采样的优化问题，分析了稀疏微波成像观测矩阵的相关系数与重建能力的关系，在此基础上提出一种基于相关系数的优化准则，并对方位向稀疏采样参数进行优化。仿真结果验证了所提优化方法的有效性。

合成孔径雷达；稀疏微波成像；方位向采样；相关准则

1 引言

随着高分辨率、宽测绘带等遥感观测要求的提出，以合成孔径雷达(SAR)[1]为代表的现代微波成像系统数据率急剧增加，对数据的获取、传输以及处理等过程带来巨大挑战。

稀疏微波成像[2]是将稀疏信号处理与微波成像理论两者相结合所形成的新理论、新体制和新方法，在降低数据率和系统复杂度、提升系统成像性能等方面具有潜在优势。当观测场景可被稀疏表征时，稀疏微波成像能够利用稀疏采样进行无模糊重建，从而降低系统数据量。稀疏采样方式是影响观测矩阵稀疏重建性质的重要因素之一[2]。相关性条件是度量观测矩阵稀疏重建性质的常用指标，稀疏信号处理方面已有若干理论分析结果[3-6]。文献[3,4]指出当未知信号的稀疏度与观测矩阵最大相关系数满足一定关系时，通过求解1最小化问题能在无噪条件下精确地、或噪声条件下稳健地重建出该信号。文献[5]进一步推导了稀疏重建误差与观测矩阵最大相关系数的数量级关系。文献[6]提出观测矩阵的平均相关系数更适合衡量观测矩阵的稀疏重建性能。在稀疏信号处理应用于雷达成像方面，相关性条件提供了稀疏采样方式影响重建质量的分析工具[7-11]。文献[7]利用点扩展函数(PSF，等价于最大相关系数)分析聚束式SAR中不同稀疏采样方式与稀疏重建结果中虚假目标严重程度的关系。文献[8]根据相关系数准则利用正交信号构造条带式SAR的观测矩阵从而提高稀疏重建性能。文献[9]提出基于平均相关系数和信噪比组合的多发多收雷达采样方式优化准则，分析不同稀疏采样方式下检测概率与虚警概率的关系。文献[10]研究了观测矩阵相关系数的分布对重建质量的影响，指出当相关系数集中分布时可使重建结果中产生较少虚假目标。文献[11]进而采用t%平均相关系数评估单站/多站聚束式SAR在不同稀疏采样下的稀疏重构质量。

条带式SAR是重要的SAR观测模式，本文主要研究条带式SAR方位向稀疏采样的优化问题。方位向稀疏采样有均匀抽取、随机抽取以及随机抖动等方式[2]，合理的稀疏采样方式能够改善观测矩阵的稀疏重建性质，在相同采样数条件下提高稀疏重建质量。由于稀疏信号处理中研究的观测矩阵多为傅里叶阵或随机阵、聚束式SAR的观测矩阵为傅里叶阵，而条带式SAR观测矩阵类似于Toeplitz矩阵，所以上述研究稀疏采样的结论[3-11]不能直接用于解决条带式SAR的方位稀疏采样优化问题。

本文综合考虑了观测矩阵的平均相关系数及其分布，提出一种基于相关系数的条带式SAR方位采样优化准则，并利用基于模拟退火原理的优化算法进行方位向稀疏采样策略的优化。仿真实验结果表明了所提优化方法的有效性。本文结构如下，第2节介绍稀疏微波成像的方位向信号模型；第3节根据条带式SAR的特点提出了单通道/多通道下基于相关系数的优化准则以及优化算法；第4节利用实验结果说明所提方法的有效性；最后给出总结。

2 信号模型

其中，列向量y, x与n分别表示回波数据、离散场景以及热噪声；观测矩阵Φ中第m行l列上的元素为

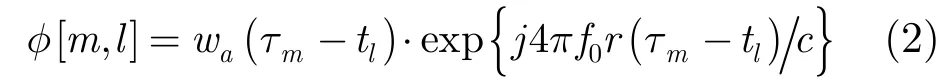
2.1 单通道SAR观测模型

条带SAR方位向信号模型可表示为

其中，τ为方位向时间，t为目标的波束中心穿越时刻；wa(⋅)为天线方位向的方向图；f0为载波频率；c为光速；r(τ-t)表示τ时刻平台与位于t目标的瞬时距离。

2.2 多通道SAR观测模型

方位向多通道模型[12]可表示为

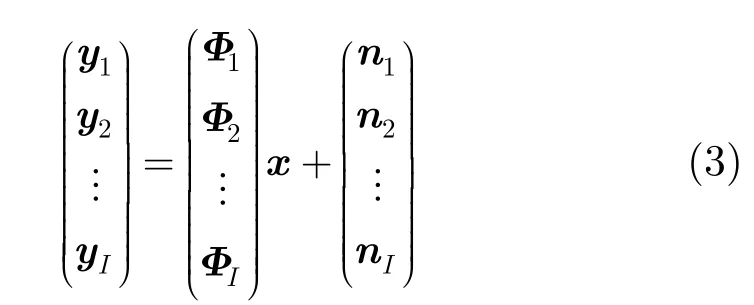
其中，yi(i=1,2,…,I )为第i通道的观测数据，I为接收通道数；Φi为相应通道的观测矩阵。假定由第1通道发射信号，则在远场条件下，第i通道的观测矩阵Φi中第m行l列的元素为

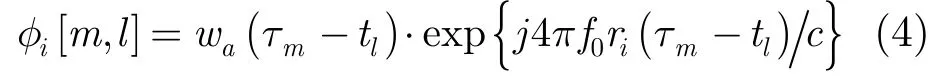
2.3 稀疏微波成像

针对上节描述的SAR观测模型，基于ql正则化的稀疏微波成像模型[2]为

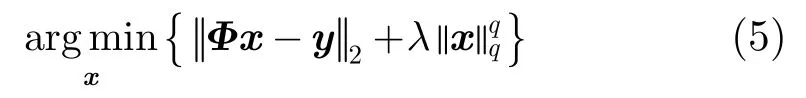
其中，λ是正则化参数，q是正则化格式，取01q＜≤获得稀疏解。由稀疏信号处理理论可知，稀疏采样方式影响观测矩阵Φ的稀疏重构性能，进而影响稀疏微波成像质量。

3 采样方式优化与设计

3.1 采样方式

稀疏微波成像的关键问题之一是研究保持成像质量同时减少回波数据量[2]。根据稀疏信号理论，稀疏采样方式是影响观测矩阵稀疏重建性质的重要因素之一，满足高斯随机分布的观测矩阵具有较优的稀疏重构性能。在信号源、采样数等其他系统参数确定的条件下，合理选择方位稀疏采样方式可获得最优观测矩阵。常见的方位向稀疏采样方式可概括如下：

(1)采样时刻mτ由目标时刻lt的线性组合构成，即

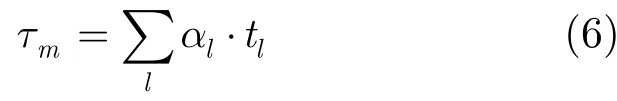
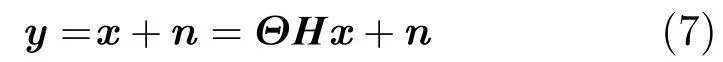
其中，满采样的SAR观测矩阵Η是Toeplitz矩阵；Θ为稀疏降采样矩阵。硬件可实施的降采样方式包括均匀抽取和非均匀抽取。非均匀抽取获得的重建质量优于均匀抽取的重建质量[2]。

(2)采样时刻mτ在均匀降采样基础上附加适当的随机抖动量：

其中，lα为系数。它可描述满足奈奎斯特采样率条件下的数据抽取模型，此时观测模型可简化为

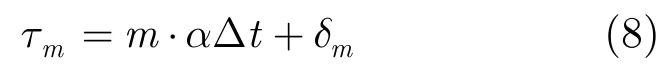
其中，α=M/L为降采样率，抖动量δm为随机变量，这种采样方式为随机抖动采样[13]。随机抖动采样的最小间隔需满足系统参数的约束。设计特定抖动序列可提高观测矩阵稀疏重建性能，改善稀疏微波成像质量，同时能够采集测绘带盲区的回波，扩大测绘带宽[14]。

3.2 优化准则

本节以基于相关性条件的准则对条带式SAR方位向采样方式进行分析与优化。观测矩阵Φ的第l与l′列之间的相关系数定义为

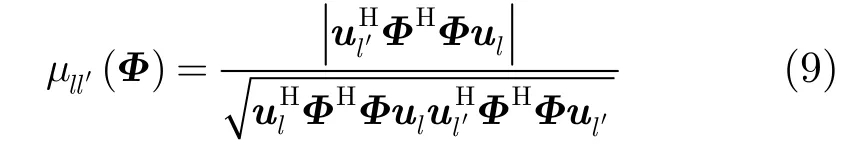
条带式SAR的方位向观测矩阵是Toeplitz矩阵，以TerraSAR-X系统条带模式[15]为例计算观测矩阵的相关系数，如图1(a)所示。观测矩阵相关系数是列间距离(l-l′)的函数，满采样时的相关系数随列间距离增大而迅速减小，如图1(b)所示；采用随机降采样时(l-l′)≠0处的相关系数都增大，如图1(c)所示；采用均匀降采样时相关系数在特定列间距离位置有较强相关性，如图1(d)所示。降采样引起特定列间距离处相关系数增大，稀疏重建时不易排除来自这些位置的干扰，进而产生虚假目标。所以考虑相关系数的分布可获得更为有效的相关系数优化准则，从而指导方位向采样方式设计。

基于上述分析以及已有的研究成果[7-11]，本文给出基于相关系数的优化准则。首先定义相关系数集合Cp，其元素构成观测矩阵相关系数中平方和最大的p(0＜p＜1)部分。

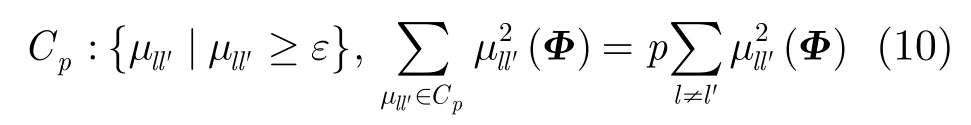
其中，ε为对应的阈值。相关系数的支撑度量pd定义为

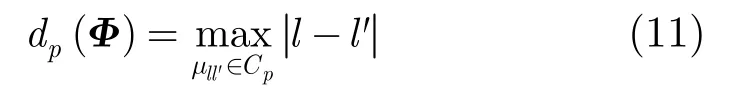
则优化准则可表示为

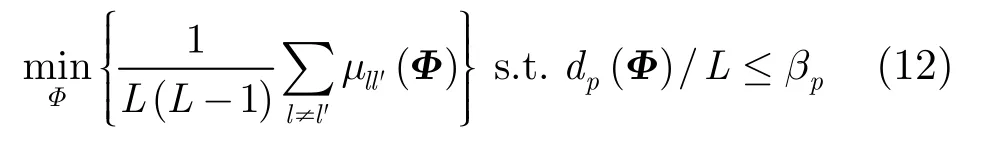
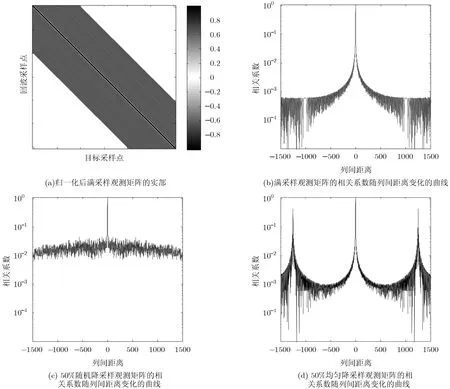
图1 条带SAR观测矩阵及不同采样方式下的相关系数示意图

其中，0＜βp＜1约束了p相关系数的支撑度量上界。该准则各项意义如下，目标函数表示观测矩阵的平均相关系数，衡量观测矩阵相关系数的整体水平；约束条件表示相关系数的分布，度量稀疏重建时允许出现的误差范围。支撑度量取合理数值范围时，较小的平均相关系数可提高稀疏微波成像的重建质量。当观测矩阵是正交阵时，∀l≠l′有μll′(Φ)=0且dp(Φ)=0。

3.2.1 单通道优化准则 利用2.1节的方位向观测矩阵可得条带式SAR观测矩阵列间相关系数为

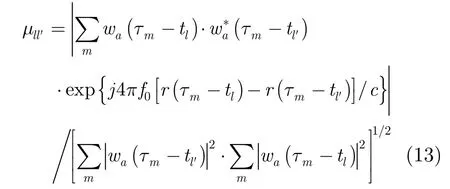
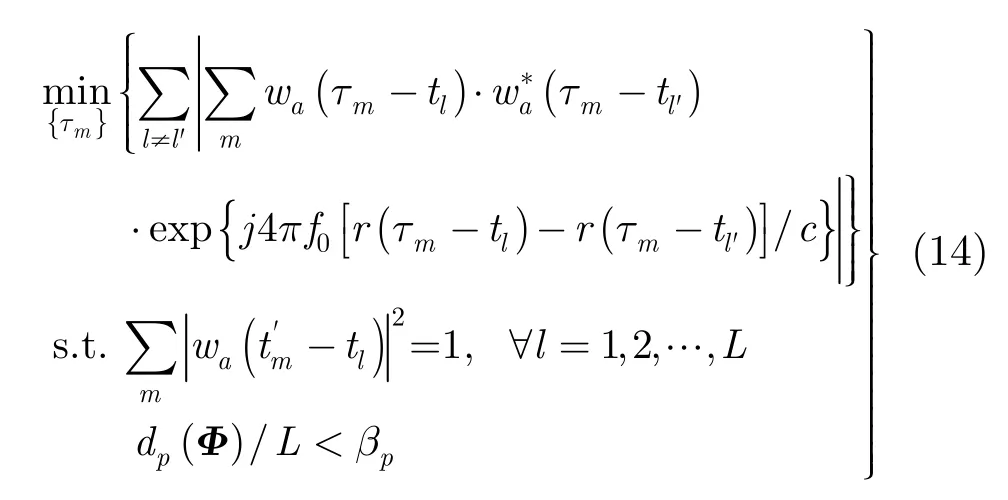
3.2.2 多通道优化准则 当方位向采用多通道技术时，观测矩阵列间相关系数为

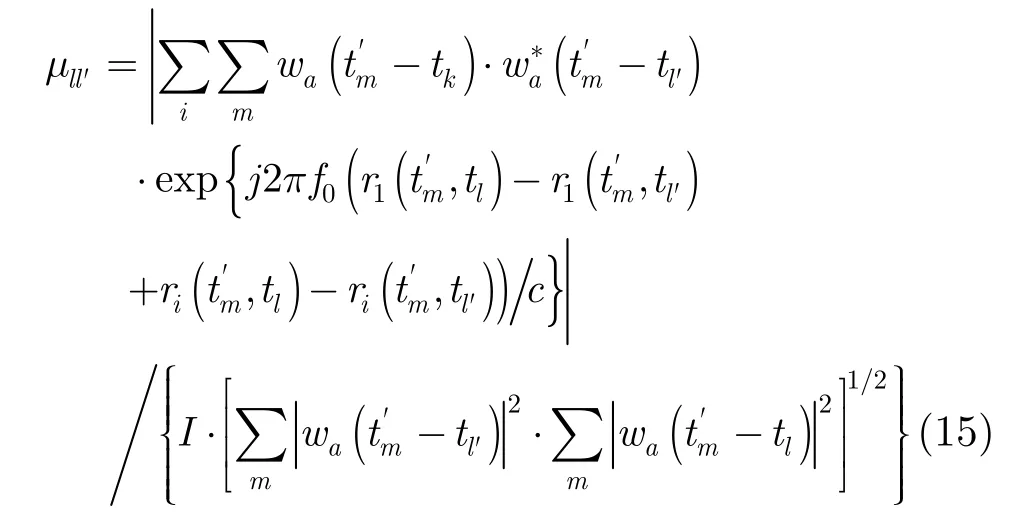
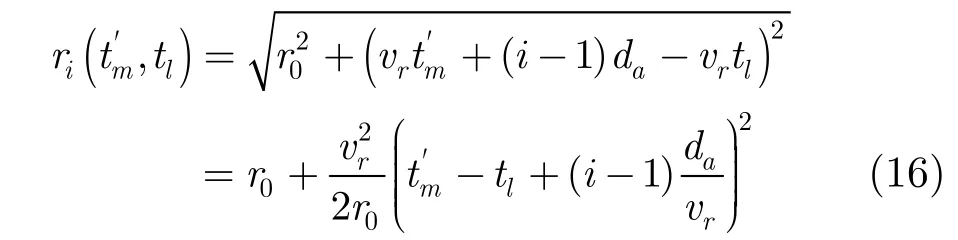
又因为

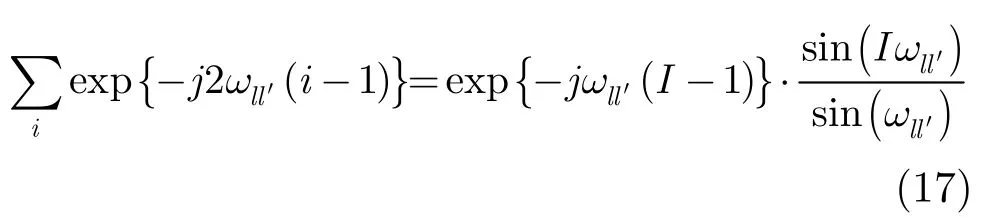
则多通道相关系数的分子绝对值之内的部分为

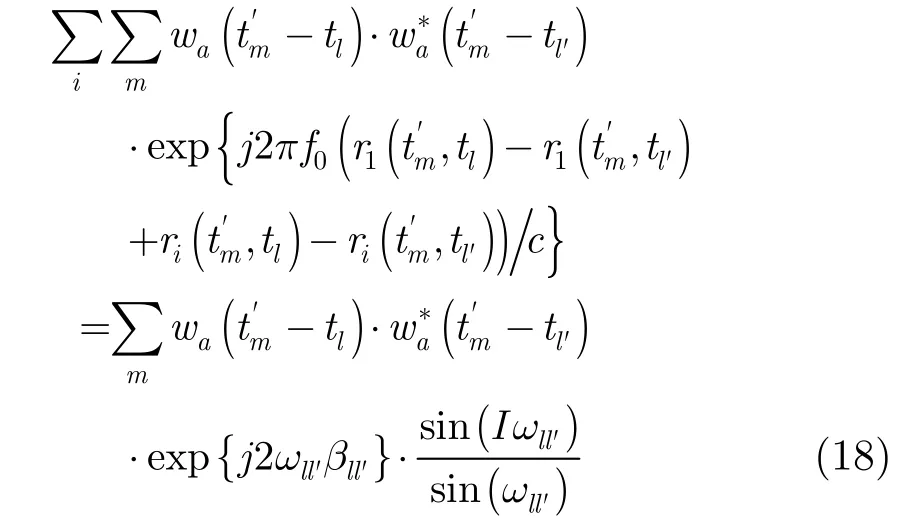
归一化观测矩阵列向量的能量后，优化准则表示为

当llω′较小时，多通道的平均相关系数近似是单通道的1/I。由于多通道优化准则与单通道的优化准则类似，下文将以单通道为例开展实验，验证本文所提准则的有效性。

式(14)，式(19)属于组合优化问题。当方位向稀疏采样方式为随机抽取时，可利用基于模拟退火[16,17]算法求解最优采样方式。该算法属于局部搜索算法，给予充足计算时间能以概率收敛到全局最优解[17]。

4 实验

本节通过仿真实验说明所提优化准则的有效性，并且验证优化采样方式在场景重建方面的优势，最后给出实际数据的成像结果。

4.1 实验1

实验1说明所提优化准则可有效评估不同稀疏采样方式下条带SAR的稀疏重建结果。仿真参数：天线长度为4.8 m，平台等效速度为7282 m/s，脉冲重复频率为3761 Hz，载波频率为9.65 GHz。场景采样点数为3072，网格分辨率为1.93 m，点目标位于场景中心。随机抽取的采样数为49616 m+,m=1,2,…,161；均匀抽取的降采样数为512m, m=1,2,…,6；随机抖动采样的最高脉冲重复频率等于3761 Hz。仿真数据利用稀疏重构算法[2,18]获得重建结果，实验采用蒙特卡洛方法重复100次。

图2是相关系数、支撑集度量以及相对均方误差rMSE的变化曲线，其中，x为场景后向散射系数真实值，xˆ为x的稀疏重建结果。由图2可知，均匀抽取和均匀降采样的支撑度量大于随机抽取和随机抖动方式的支撑度量，故均匀抽取和均匀降采样的rMSE高于随机抽取和随机抖动的rMSE。由于均匀采样方式相关系数分布还存在如图1(b)所示的峰值，且其能量在降采样50%左右存在最大值，所以均匀抽取与均匀降采样的支撑度量存在先增后减的变化。另外，由图2(c)可知，当降采样率较小时，保持相同最小采样间隔时随机抖动采样的rMSE略大于随机抽取的rMSE；而降采样率增加到80%左右时，前者的rMSE则略小于后者的rMSE，这也与80%降采样率时随机抖动的支撑度量较低相对应。

4.2 实验2

实验2说明所提优化采样方式能有效提高观测矩阵的稀疏重建性质。目标幅度为1，相位在(],ππ-之间，目标随机分布在场景中；降采样率为40%。无噪条件下，目标数为采样数的0.25%～10%，采用蒙特卡洛方法重复1000次；有噪条件下，信噪比为目标数为采样数的10%，采用蒙特卡洛方法重复500次。

图3是优化采样、随机抽取以及均匀降采样的正确重建概率、虚假目标概率以及rMSE分布情况。正重建概率定义为，虚假目标概率定义为，其中，T表示目标位置的集合，为T的补集，δ为允许误差范围(实验取0.99),表示计算非零元素的个数。由图3(a), 3(b)可知，当稀疏度为10%时，优化采样方式的正确重建概率比随机抽取、均匀降采样的分别高出5%，10%，且其虚假目标概率比随机抽取、均匀降采样低了一倍。另外，由图3(c)可知，SNR=20 dB时，优化采样下的rMSE比随机抖动、均匀降采样分别小了20%和50%。所以，在相同条件下，采用优化采样方式能恢复更多目标，且减少虚假目标出现概率；在信噪比合适时，优化采样方式能有效提高重建质量。

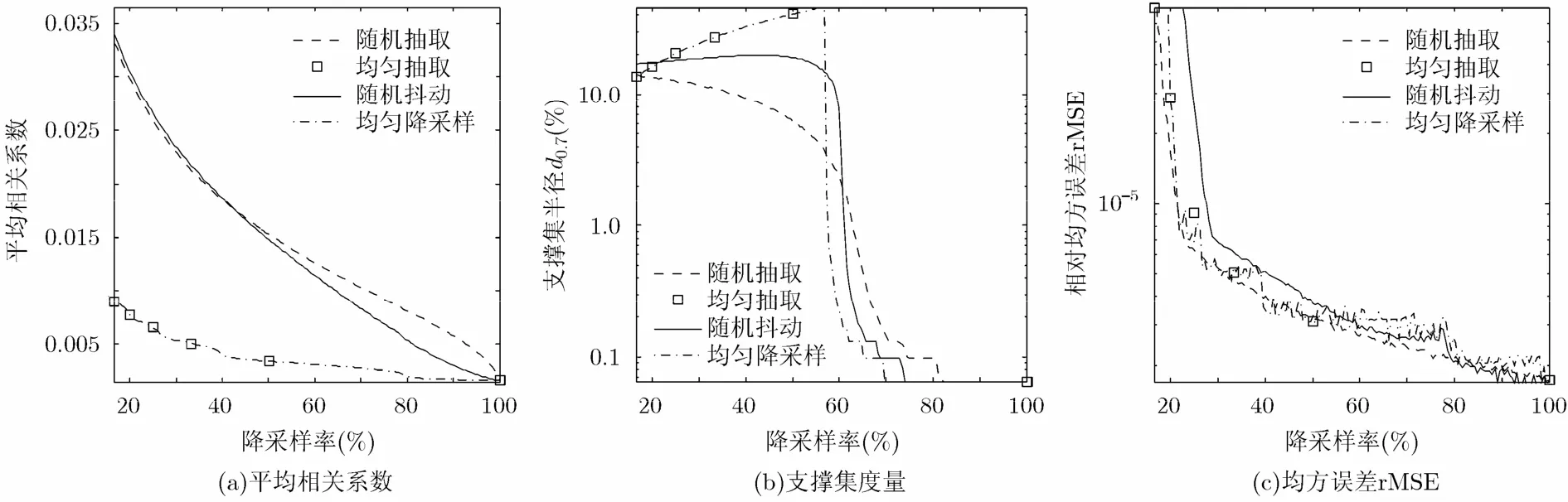
图2 不同降采样方式与相关系数、支撑集度量以及rMSE的关系曲线

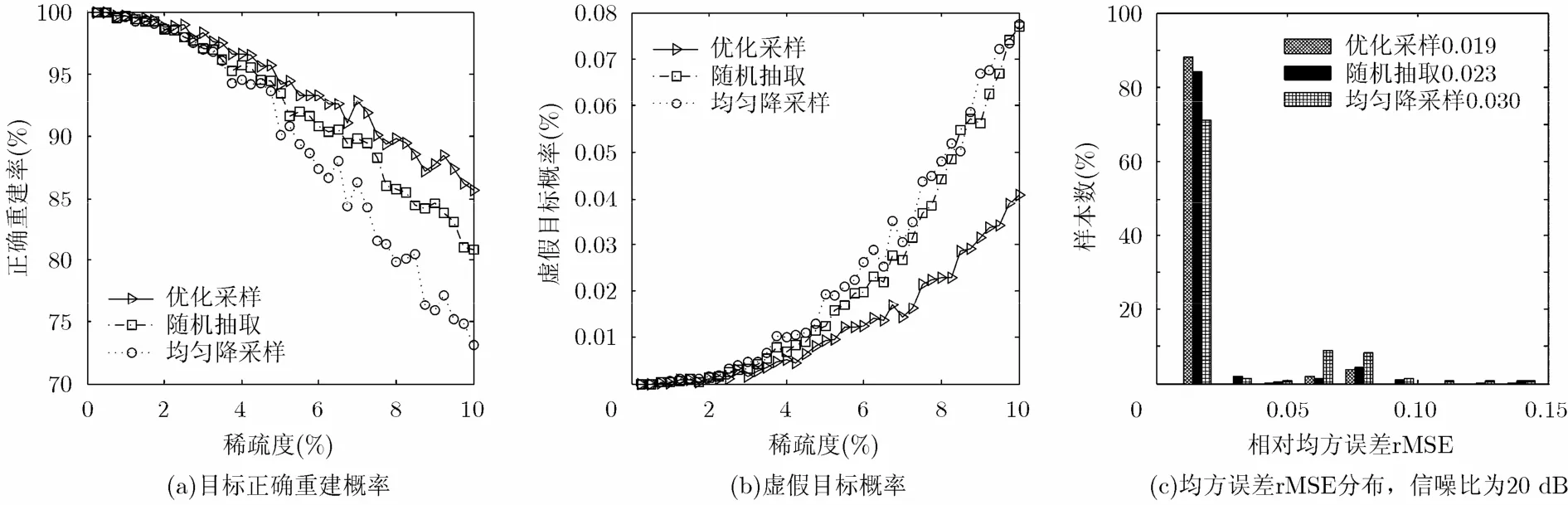
图3 优化的采样方式、随机抽取采样方式以及均匀降采样方式的稀疏重建性能

图4 RadarSat场景常规成像结果与稀疏微波成像结果，能量经过归一化

4.3 实验3

实验3说明优化采样方式可用于实际数据的稀疏微波成像。图4为RadarSat数据[19]满采样、75%均匀抽取、75%优化降采样下，常规成像结果与稀疏微波成像结果对比。其中，优化降采样方式的结果略优于随机抽取，故不展示随机抽取的结果。由图4可知，降采样引起的方位模糊与强目标旁瓣分别在稀疏微波成像中得到抑制，同时图像灰度对比度也提高了。

5 结论

本文研究了相关系数对条带式SAR观测矩阵稀疏重建性质的影响，在此基础上提出一种基于相关系数的方位向采样优化准则以及基于模拟退火的方位稀疏采样优化算法；仿真实验结果验证了所提准则和优化算法的有效性。

[1] Wiley C. Synthetic aperture radars: a paradigm for technology evolution[J]. IEEE Transactions on Aerospace and Electronic Systems, 1985, 21(3): 440-443.

[2] Zhang Bing-chen, Hong Wen, and Wu Yi-rong. Sparse microwave imaging: principles and applications[J]. SCIENCE CHINA Information Sciences, 2012, 55(8): 1722-1754.

[3] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[4] Donoho D, Elad M, and Temlyakov V. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Transactions on Information Theory, 2006, 52(1): 6-18.

[5] Cai T, Wang L, and Xu G. Stable recovery of sparse signals and an oracle inequality[J]. IEEE Transactions on Information Theory, 2010, 56(7): 3516-3522.

[6] Bajwa W, Calderbank R, and Mixon D. Two are better than one: fundamental parameters of frame coherence[J]. Applied and Computational Harmonic Analysis, 2012, 33(1): 58-78.

[7] Patel V, Easley G, Healy D, et al.. Compressed synthetic aperture radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 244-254.

[8] 江海, 林月冠, 张冰尘, 等. 基于压缩感知的随机噪声成像雷达[J]. 电子与信息学报, 2011, 33(3): 672-676.

Jiang Hai, Lin Yue-guan, Zhang Bing-chen, et al.. Random noise imaging radar based on compressed sensing[J]. Journal of Electronics & Information Technology, 2011, 33(3): 672-676.

[9] Yu Y, Petropulu A, and Poor H. Measurement matrix design for compressive sensing–based MIMO radar[J]. IEEE Transactions on Signal Processing, 2011, 59(11): 5338-5352.

[10] Bar-Ilan O and Eldar Y. Sub-Nyquist radar via Doppler focusing[J]. IEEE Transactions on Signal Processing, 2014, 62(7): 1796-1811.

[11] Stojanovic I, Çetin M, and Karl W. Compressed sensing of monostatic and multistatic SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6): 1444-1448.

[12] Currie A and Brown M. Wide-swath SAR[J]. IEE Proceedings F : Radar and Signal Processing, 1992, 139(2): 122-135.

[13] Balakrishnan A. On the problem of time jitter in sampling[J]. IRE Transactions on Information Theory, 1962, 8(3): 226-236.

[14] Hong Wen, Zhang Bing-chen, Zhang Zhe, et al.. Radar imaging with sparse constraint: principle and initial experiment[C]. Proceedings of 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 2014: 1-4.

[15] Werninghaus R. TerraSAR-X mission[C]. Proc. SPIE 5236, SAR Image Analysis, Modeling, and Techniques VI, Barcelona, Spain, 2004: 9-16.

[16] Metropolis N, Rosenbluth A, Rosenbluth M, et al.. Perspective on equation of state calculations by fast computing machines[J]. Journal of Chemistry and Physics, 1953, 6(21): 1087-1092.

[17] Granville V, Krivánek M, and Rasson J. Simulated annealing: a proof of convergence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(6): 652-656.

[18] Tian Ji-hua, Sun Jin-ping, Lu Song-tao, et al.. NUFFT-based fast reconstruction for sparse microwave imaging[J]. Journal of Electromagnetic Waves and Applications, 2013, 27(4): 485-495.

[19] Cumming I and Wong F. Digital Signal Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Norwood, MA, US, Artech House, 2004: Appendix A.

蒋成龙： 男，1987年生，博士，研究方向为SAR信号处理、星载稀疏微波成像系统设计与信号处理.

赵 曜： 男，1984年生，研究员，研究方向为稀疏信号处理、稀疏微波成像性能研究.

张 柘： 男，1988年生，博士，研究方向为信号与信息处理、稀疏微波成像算法.

张冰尘： 男，1973年生，研究员，研究方向为信号与信息处理、雷达信号处理与系统设计.

洪 文： 女，1968年生，研究员，博士生导师，研究方向为信号与信息处理、雷达信号处理与系统设计.

Azimuth Sampling Optimization Scheme for Sparse Microwave Imaging Based on Mutual Coherence Criterion

Jiang Cheng-long①②③Zhao Yao①②Zhang Zhe①②③Zhang Bing-chen①②Hong Wen①②①(Science and Technology on Microwave Imaging Laboratory, Beijing 100190, China)
②(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
③(University of Chinese Academy of Sciences, Beijing 100190, China)

Sparse microwave imaging is a novel theory that systematically introduces sparse signal processing to microwave imaging. Compared with conventional synthetic aperture radar imaging, sparse microwave imaging exhibits the advantage of better imagery quality and lower system complexity. Non-ambiguity reconstruction for sparse scene can be achieved on under-sampling raw data by means of sparse microwave imaging, which leads to total data amount reduction. The imagery quality of sparse microwave imaging depends on the recovery property of measurement matrix, which is affected by the sparse sampling strategy. This paper focuses on the problem of design the azimuth sparse sampling scheme. The connection between mutual coherence and recovery property of the measurement matrix is analyzed. A mutual coherence based criterion is then proposed and applied to optimize the existing azimuth sparse sampling scheme. Numerical results demonstrate the effectiveness of the proposed method and conclusions are discussed.

SAR; Sparse microwave imaging; Azimuth sampling; Mutual coherence criterion

TN957.52

A

1009-5896(2015)03-0580-07

10.11999/JEIT140613

2014-05-12收到，2014-08-29改回

*通信作者：蒋成龙 chenglong.j@gmail.com