1-Bit压缩感知盲重构算法

张京超 付 宁杨 柳

(哈尔滨工业大学自动化测试与控制系 哈尔滨 150080)

1-Bit压缩感知盲重构算法

张京超 付 宁*杨 柳

(哈尔滨工业大学自动化测试与控制系 哈尔滨 150080)

1-Bit压缩感知(CS)是压缩感知理论的一个重要分支。该领域中二进制迭代硬阈值(BIHT)算法重构精度高且一致性好，是一种有效的重构算法。该文针对BIHT算法重构过程需要信号稀疏度为先验信息的问题，提出一种稀疏度自适应二进制迭代硬阈值算法，简称为SABIHT算法。该算法修正了BIHT算法，首先通过自适应过程自动调节硬阈值参数，然后利用测试条件估计信号的稀疏度，最终实现不需要确切信号稀疏度的1-Bit压缩感知盲重构。理论分析和仿真结果表明，该算法较好地实现了未知信号稀疏度的精确重建，并且与BIHT算法相比重构精度及算法复杂度均相当。

压缩感知；1-Bit压缩感知；盲重构；二进制迭代硬阈值

1 引言

压缩感知理论[1-3]是近年发展起来的新的信号获取和信号处理理论。该理论表明，对于稀疏或可压缩信号，通过远低于奈奎斯特采样速率采样，可精确地实现原始信号恢复。在数字信号处理和数字通信系统中，信号量化是必不可少的一部分。随着信息技术不断发展，信号频带宽度不断增大，为了满足人们的信息需求，需要提高采样速率和量化精度，这将对采样系统中模拟数字转换器件(Analog to Dgital Converter, ADC)、存储器件的选择及数据传输提出了比较严峻的挑战。压缩感知理论虽然实现了低速采样，在一定程度上缓解了ADC压力，但是为了提高重构精度，仍需要增加信号的观测数量和提高观测值的量化精度[4,5]。无论是提高采样速率还是量化精度，都会造成数据量增大，量化仍然是压缩感知中数据压缩的重要一步。近年来，量化压缩感知[4-7]受到广泛关注，人们从降低采样速率的角度转换为降低量化精度的角度，试图通过低精度量化缓解硬件压力。2008年，文献[8]提出对测量值进行极限量化，即1-Bit量化，也能实现稀疏信号重构。1-Bit压缩感知是将压缩观测值进行极限量化处理，通过保留观测值的符号信息，缓解硬件压力，提高存储效率，并克服测量中的动态范围问题。1-Bit压缩感知的重构算法可分为两大类：凸算法与非凸贪心算法。文献[8]在固定点连续(Fixed Point Continuation, FPC)算法的基础上，增加梯度投影和球面约束思想，提出BFPC(Binary FPC)算法，该算法为凸正则化算法。匹配符号追踪算法(Matching Sign Puisuit, MSP)[9]是在CoSaMP算法的基础上提出的一种贪心算法。文献[10]介绍了类似于非凸优化中的信赖域算法––限制步长收敛算法(Restricted Step Shrinkage, RSS)，该算法具有较好的收敛性，计算速度快，重构信噪比较高。文献[11]提出二进制迭代硬阈值算法(Binary Iterative Hard Thresholding, BIHT)，文献[5]提出的1-Bit线性规划算法(One-Bit linear programming)，文献[12]提出一种快速精确的两级 (Fast and Accurate Two-Stage, FATS)信号重构算法，在上述算法中最突出的算法是BIHT算法，该算法较其它重构算法的重够效果更好，表现为较高的重构信噪比和一致性，且计算过程简单，复杂度低[13]。BIHT算法虽然具有较完美的重构效果，但是该算法要求信号的稀疏度作为重构的先验条件。在实际应用中，获取信号稀疏度是相当困难的。针对BIHT算法要求信号的稀疏度已知的问题，该文在其基础上进行改进，提出稀疏度自适应二进制迭代硬阈值(Sparsity Adaptive Binary Iterative Hard Thresholding, SABIHT)算法。该算法通过增加稀疏度自适应过程，很好地克服了BIHT算法对信号稀疏度依赖性的问题，实现了1-Bit压缩感知盲重构，在不影响重构精度的前提下，有效克服实际中信号稀疏度未知的问题。

本文在第2节介绍了压缩感知模型与1-Bit压缩感知模型；第3节首先分析BIHT算法，然后描述1-Bit压缩感知盲重构算法的具体实施方法；第4节给出不同情况下SABIHT算法与BIHT算法的性能比较试验，通过分析仿真结果说明改进算法的有效性；第5节对该方法进行总结。

2 压缩感知背景

2.1 压缩感知模型

信号的稀疏性是压缩感知理论应用的前提。假设实值离散时间信号x∈是N×1维列向量。空间的任何信号都可以用N×N维的规范正交基向量{ψi}的线性组合表示。则x在一组正交基下进行展开，即

其中系数向量为α=[α,α,⋅⋅⋅,α]T。如果信号x在

12N正交基Ψ下的系数向量α中最多含有K个非零元素，则称向量α为信号的x稀疏表示，即a=Ψ-1x=ΨTx ，信号x则称为稀疏信号。

其中Φ为M×N(M＜＜N)维观测矩阵。利用M维观测值y恢复信号x的过程称为信号重构，重构模型可写为

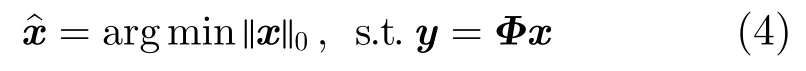
求解式(4)的本质是0l范数最小化求解问题，是NP难问题，无法直接求解。当前这类问题的间接求解方法较多，其中贪婪迭代算法因算法结构简单、运算量小而颇受关注，主要有匹配追踪(Matching Pursuit, MP)[14]、正交匹配追踪(Orthogonal Matching Pursuit, OMP)[15]及子空间追踪(Subspace Pursuit, SP)[16]等。

2.2 1-Bit压缩感知模型

在现实环境中，观测值y必须经过量化处理后，才能进行数字处理，进而恢复信号。量化模型[17]可写为

其中BQ表示B-Bit量化，即将观测值量化为B位二进制数。当B取值为1时，表示1-Bit量化。1-Bit量化是对观测值进行量化处理的一种极限情况，即仅保留观测值的符号信息[8]。测量值的1-Bit量化具有的优势为[10]：1-Bit量化通过比较器实现，比较器代替ADC可以极大地提高运行速率，简化硬件结构；避免受动态量程的影响，当模拟输入端受适当的影响时，测量值的符号依旧有效；在输入信噪比水平较低时，总比特位数固定时1-Bit CS优于多Bit CS。

通常情况下，量化过程电压比较器的比较电压取为零[8]，则1-Bit压缩感知量化模型可写为

其中，sign(⋅)为符号函数。观测值向量y可构成M×M的对角矩阵Y=diag(y)。根据符号一致性原理，可得YΦx≥0。1-Bit压缩感知仅保留观测值的符号，信号的幅度信息丢失，重构模型用l1范数作为衡量信号稀疏性标准。为了确保得到非零解，并克服幅度不确定性问题，在单位l2球面上重构信号。1-Bit压缩感知重构模型为

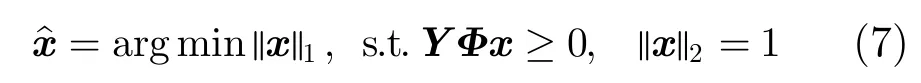
1-Bit压缩感知理论自提出以来，受到了学者们的广泛关注并提出许多有效算法。BIHT算法的重构效果优于MSP和RSS算法，主要表现为重构过程简单，较高的重构信噪比和一致性，详见文献[11]。但是BIHT算法要求信号的稀疏度K作为先验信息，然而在实际应用中信号的稀疏度K通常是未知的，这在相当程度上限制了上述算法的应用。

3 1-Bit压缩感知盲重构

3.1 传统的BIHT算法

BIHT算法最初是在迭代硬阈值(Iterative Hard Thresholding，IHT)算法[18]的基础上改进的。IHT算法是处理压缩感知问题的一种常用算法，该算法是求解满足约束条件优化问题，文献[18～20]推导出了IHT算法理论，IHT算法十分简洁，采用迭代式(8)：

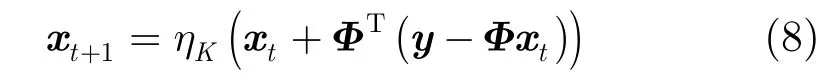
其中xt为第t次迭代值，ηK(β)是一个非线性算子，它将矢量β中幅度最大的前K个元素以外的所有元素设置为零。

IHT算法的迭代式(8)可分解为两步，第1步在第t次迭代中令矢量，通过梯度下降法减小目标的平方差；第2步将1t+β映射到0l范数球面上，得到稀疏解。

BIHT算法结合1-Bit压缩感知特点，用最小一致目标代替IHT算法的第1步，即在第l次迭代中令，并令残差r=yt-sign(Φxt)；第2步将βt+1映射到l2范数单位超球面上，并保留前K个最大值元素，其余元素置为零。BIHT算法的具体重构原理框图如图1所示。

如图1所示，重构时首先利用观测值进行初始估计，然后进行硬阈值投影，即将估计值以参数K为硬阈值，投影到单位超球面上，并保留前K个最大值元素，其余元素置为零，然后更新信号，更新残差后继续迭代。

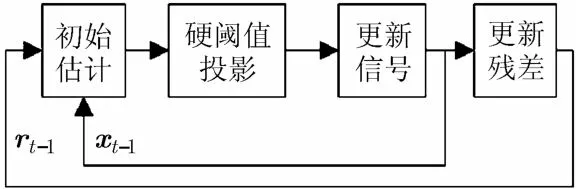
图1 BIHT算法重构原理图

3.2 BIHT算法稀疏度依赖性问题分析

由于BIHT算法采用信号稀疏度K作为迭代过程中的硬阈值条件，信号稀疏度K成为该算法有效应用的一个必要前提。为了说明信号稀疏度K值不准确对BIHT重构算法的影响，进行如下仿真实验。仿真信号为高斯随机稀疏信号，长度N=256，信号稀疏度K=20，观测值个数M=300, 400, 500, 600，700，感知矩阵Φ服从高斯分布[21]。实验中利用BIHT算法进行重构，重构算法采用估计稀疏度，依次取值为10, 15, 20, 25, 30，实验运行100次。仿真结果如图2所示。

通过观察图2结果，说明稀疏度K值不准确对BIHT算法重构效果的影响明显。稀疏度估计值取为20时，BIHT算法重构信噪比最高，稀疏度估计值大于或小于真实值K=20，都会不同程度的影响BIHT算法的重构效果，其中K=10时，重构效果最差。由此可以得出结论，信号稀疏度K不准确，将造成BIHT算法的重构效果明显变差，即BIHT重构算法存在信号稀疏度依赖性问题。

3.3 稀疏度自适应二进制迭代硬阈值(SABIHT)算法

由于BIHT重构算法将信号稀疏度K作为重构的硬阈值条件，从而保证重建的精确性。为了克服BIHT算法的稀疏度依赖性问题，该文在BIHT算法的基础上增加稀疏度自适应的过程，提出SABIHT重构算法。图3给出了该算法的原理框图。

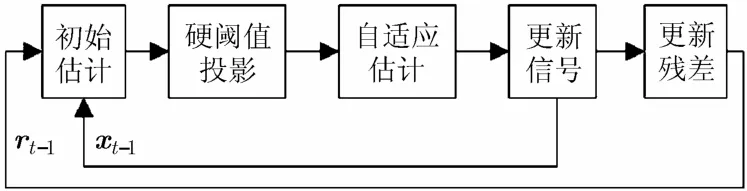
图3 SABIHT算法重构原理图

如图3所示，SABIHT的重构思想是：在BIHT算法的基础上引入稀疏度自适应[21]方法，自适应地估计阈值参数，利用估计硬阈值更新信号。具体实施方法为：选择固定的步长s作为初始硬阈值参数，通过测试条件判断估计硬阈值是否满足要求，并控制硬阈值参数以s为步长逐渐逼近信号稀疏度K，最终利用估计的硬阈值参数按照BIHT原理恢复信号。该算法的测试条件包括相邻两阶段重建信号的能量差和残差能量的大小。SABIHT重构算法通过上述过程实现自适应的估计信号稀疏度，克服了BIHT算法直接将稀疏度K作为硬阈值，过度依赖稀疏度的问题。算法的具体实施步骤如表1所示。

SABIHT算法，首先设定初始步长s＜K作为迭代的初始硬阈值参数，然后判断相邻两次迭代信号的能量差和残差大小，确保迭代向收敛方向发展。当相邻两次迭代信号的能量差小于参数ε时，此时的硬阈值大小(估计稀疏度L)最接近信号稀疏度，再利用L恢复原信号。步骤(1)到步骤(3)，实现了稀疏度的粗估计和迭代变量的初始化。步骤(4)到步骤(8)，为SABIHT重构算法在BIHT框架下的稀疏自适应迭代部分。

SABIHT算法是在BIHT框架下融合稀疏自适应策略而得到，该策略将对算法的收敛速度产生影响但并不影响算法的收敛性。而BIHT是迭代硬阈值(IHT)的改编算法，研究人员从数值仿真实验角度证明了其收敛性[11]，而IHT算法则有完善的理论分析证明其至少收敛到一个局部点[22]。基于上述成果，本文得出SABIHT算法至少能收敛到一个局部点。算法收敛时的稀疏度为与真实的稀疏度K近似相等，从而在未知稀疏度的前提下，实现了重构。SABIHT重构算法每次迭代的运算量主要集中在表1中的步骤(2)和步骤(3)中，复杂度为()OMN，这与BIHT算法是一致的。SABIHT重构算法的计算复杂度与迭代次数有密切关系。当步长固定时，步长的选择直接影响到迭代次数，步长s越小，重建迭代次数越多，因此在重建过程中应选取适当的步长，具体分析见4.3节。

4 实验结果及分析

为了保证该文重建算法性能的有效性和客观性，该文通过MATLAB处理平台对提出的SABIHT算法和BIHT算法进行了实验仿真。实验中BIHT算法采用的是Jacques L个人网站的程序包(http://perso.uclouvain.be/laurent.jacques)。第4.1节和4.2节通过比较无噪声情况两种重构算法的重构信噪比和噪声情况下的重构信噪比，验证了本文算法的有效性。第4.3节给出了步长选取对本文算法的影响分析实验。

表1 SABIHT算法流程

4.1 无噪声情况下SABIHT算法与BIHT算法重建性能比较

4.1.1 高斯信号的重构信噪比比较 在该实验中首先采用高斯稀疏信号[21]，测量矩阵为高斯矩阵。假设信号长度N=256，测量值个数M从50增加到600，以50为步进变化，初始步长s=10，最大迭代次数nIter=1000，对于不同的观测值M分别做100次实验，分别比较改进算法与BIHT算法在信号稀疏度K=20, 40, 60平均重构信噪比(重构信噪比之和除以实验次数)。仿真中BIHT算法给定信号稀疏度，SABIHT重构算法未给定信号稀疏度，比较结果如图4所示。

输入信号x与重构信号xˆ之间的信噪比[1]计算公式为

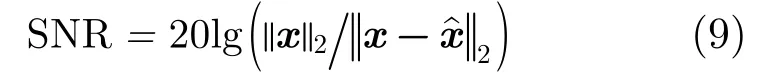
由图4可以看出在相同实验条件下，对稀疏度不同的高斯稀疏信号进行重构，SABIHT算法在信号稀疏度未知的情况下与BIHT算法已知信号稀疏度的情况下的重构效果基本一致，均随着观测值个数增加，分别由-2 dB增加到22 dB, 15 dB和12 dB。SABIHT算法放宽了实验已知条件，仍可以达到较好的重构效果，克服了实际应用中信号稀疏度难以获得的问题。

4.1.2 伯努利信号重构信噪比比较 为了说明提出算法的有效性和正确性，该实验中采用伯努利稀疏信号[21]作为原始信号，测量矩阵为高斯矩阵。假设信号长度N=256，测量值个数M从50增加到600，对于不同的观测值M分别做100次实验，分别比较SABIHT算法与BIHT算法在信号稀疏度K=20, 40, 60平均重构信噪比(重构信噪比之和除以实验次数)。重构结果如图5所示。

图4和图5的实验结果说明1-Bit压缩感知盲重构算法在信号稀疏度未知的情况下，对于高斯稀疏信号和伯努利稀疏信号，均可实现较高的重构信噪比——与BIHT算法重构信噪比基本一致。

4.2 噪声情况下SABIHT与BIHT算法重建性能比较

1-Bit压缩感知在量化过程中对观测值进行非线性量化，得到的测量值向量为符号向量。在实际测量中，由于噪声的影响，会使测量值符号发生变化。当测量值符号变化后，准确恢复原信号变得更加困难。该部分着重分析，当信号受噪声影响时，提出SABIHT算法的重构效果。

4.2.1 含噪声时高斯信号的重构信噪比比较 该实验中采用高斯稀疏信号作为原始信号，测量矩阵为高斯矩阵。假设信号长度N=256，测量值个数M=300, 350, 400，受噪声影响的符号位个数p=1(观测值中存在某一观测值符号因噪声发生符号翻转)[22,23]，信号稀疏度K=10, 20, 30, 40, 50, 60，步长s=10，对于不同的信号稀疏度K分别做100次实验，分别比较本文算法与BIHT算法在噪声情况下的重构信噪比。

图6表明，在噪声情况下SABIHT算法和BIHT算法对高斯信号的重构信噪比，均随着观测值个数增加而提高。信号稀疏度越大，两种算法的重构精度都降低，但是提出算法的重构效果略高于BIHT算法。

4.2.2 含噪声时对伯努利信号重构信噪比比较 该实验中实验信号采用稀疏伯努利信号，实验条件与4.2.1节的条件相同，实验结果如图7所示。

4.2.1 节和4.2.2节中SABIHT算法与BIHT算法针对不同信号的重构信噪比结果图说明，在噪声情况下不同信号稀疏水平时，本文提出算法与BIHT算法的重构信噪比基本一致，均随着观测值个数增加。1-Bit压缩感知盲重构算法在噪声情况下，仍可以实现未知信号稀疏度条件下的精确重构。

4.3 步长s对SABIHT算法影响分析实验

本节为考察SABIHT算法重构过程中，步长选取对重构信噪比和算法复杂度的影响，进行如下仿真实验。实验采用伯努利稀疏信号，信号维数N=256，观测值个数M=300，信号稀疏度K=10, 20, 30, 40, 50, 60，实验中SABIHT算法的步长分别取s=1, 5, 10，实验运行100次，分别比较SABIHT算法与BIHT算法的重构信噪比和所需迭代次数。比较结果如图8，图8(a)为重构信噪比的比较，图8(b)为重构所需迭代次数的比较图。

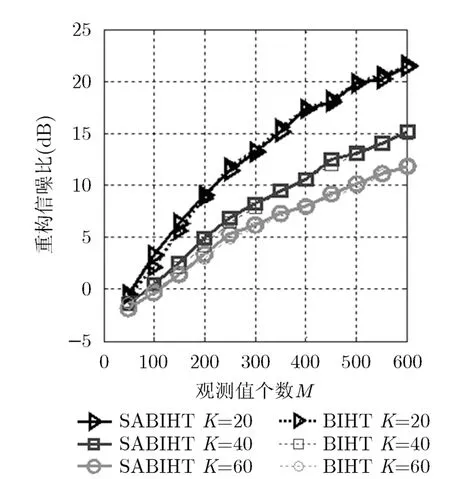
图4 无噪声时SABIHT算法与BIHT算法对高斯信号重构信噪比

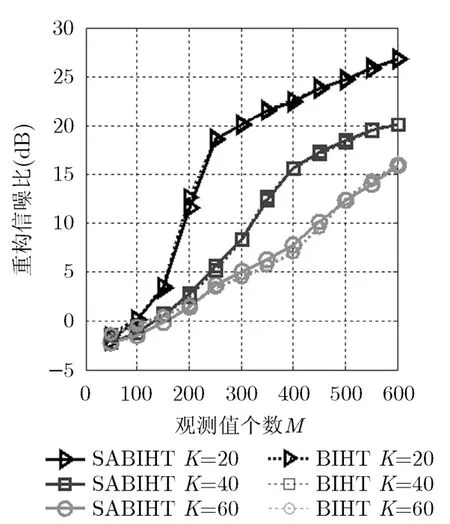
图5 无噪声时SABIHT算法与BIHT算法对伯努利信号重构信噪比

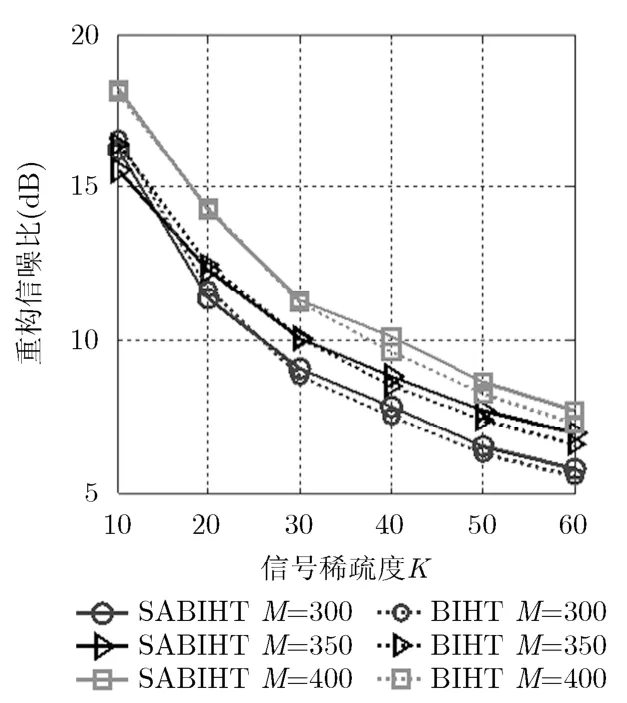
图6 含噪声时SABIHT算法与BIHT算法对高斯信号重构信噪比

图7 含噪声时SABIHT算法与BIHT算法对伯努利信号重构信噪比

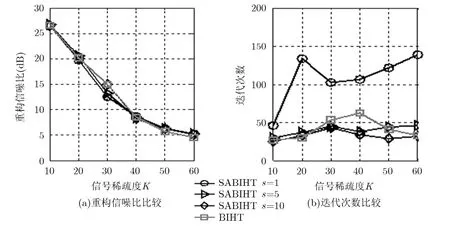
图8 SABIHT算法不同步长时的重构信噪比和迭代次数比较

从图8(a)可以看出，随着信号稀疏度递增，SABIHT算法步长s=1的重构信噪比与步长s=5的重构信噪比相当，步长s=10的重构效果更接近BIHT算法。从图8(b)可以看出，步长的选取影响SABIHT算法重构所需的迭代次数。当s=1时，迭代次数明显高于其它步长时的迭代次数。当s=10时，SABIHT算法的迭代次数甚至小于信号稀疏度已知时BIHT算法的迭代次数。在SABIHT算法中，K首先被设定为一个初值，然后按照一定的迭代步长不断累加。迭代过程中，随着K取值的增大，硬阈值操作保留的元素个数逐渐增大，这和BIHT算法每次迭代硬阈值操作保留的元素个数保持不变(即信号的真实稀疏度)不同。在一定的条件下，SABIHT算法这种策略有助于减小原子的误匹配，当算法的估计稀疏度达到真实稀疏度时，仅需少量的迭代次数即可实现信号恢复。算法总体迭代次数小于BIHT算法的迭代次数。而当步长参数较小时，比如1s=，当算法的估计稀疏度达到真实值时，算法的迭代次数已经达到较大的值，甚至大于BIHT算法的迭代次数，因而SABIHT算法在此条件下的迭代次数通常大于BIHT算法的迭代次数。仿真实验证明步长越大，所需迭代次数越少，计算复杂度越小，同时步长的增大并没有使重构精度受到影响。究其原因是因为当步长增大时，重构过程中相邻信号的能量差与残差变化更明显，从而确保逼近过程更准确。

因为信号的稀疏度是未知的，增大步长会降低算法的迭代次数，从而降低算法的复杂度。但步长较大，易使迭代过程中估计稀疏度大于信号的真实稀疏度，从而带来较大的估计误差，这从图2所示的实验结果可以看出。通常步长设置为1，然后通过迭代不断逼近信号的真实稀疏度。但此时算法复杂度较大。步长参数对算法的复杂度有较大的影响。如何选取合适的步长参数，是算法后续研究的一个问题。

5 结束语

本文针对1-Bit压缩感知重构算法中，BIHT这一经典算法重构过程中要求信号的稀疏度已知的问题，提出了一种1-Bit压缩感知盲重构算法——稀疏度自适应二进制迭代硬阈值算法，即SABIHT算法。所提出SABIHT算法在重构中可以不需要确切的稀疏度信息，自适应地估计信号稀疏度，利用估计稀疏度实现信号恢复。实验结果表明，在未知稀疏度的前提下，无论在无噪声情况与有噪声情况下，该算法的性能与已知确切稀疏度的BIHT算法相当，可以较好地实现盲重构，本文算法重构效果稳定，不易受步长影响。本文所提出的1-Bit压缩感知盲重构方法为实际1-Bit压缩感知理论的应用提供了一种有效途径。

[1] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[2] 甘伟, 许录平, 苏哲. 一种压缩感知重构算法[J]. 电子与信息学报, 2010, 32(9): 2151-2155.

Gan Wei, Xu Lu-ping and Su Zhe. A recovery-algorithm for compressed sensing[J]. Journal of Electronics & Information Technology, 2010, 32(9): 2151-2155.

[3] 贾琼琼, 吴仁彪. 基于压缩感知的空时自适应动目标参数估计[J]. 电子与信息学报, 2013, 35(11): 2714-2720.

Jia Qiong-qiong and Wu Ren-biao. Space time adaptive paratmeter estimation of moving taeget based on compressed sensing[J]. Journal of Electronics & Information Technology, 2013, 35(11): 2714-2720.

[4] Wang H T, Ghosh S, and Leon-Salas W D. Compressive sensing recovery from non-ideally quantized measurements[C]. Proceedings of the 2013 IEEE International Symposium on Circuits and Systems(ISCAS), Beijing, China, 2013: 1368-1371.

[5] Plan Y and Vershynin R. One-bit compressed sensing by linear programming[J]. Communication on Pure and Applied Mathematics, 2013, 66(8): 1275-1297.

[6] Zhou Tian-yi and Tao Da-cheng. K-Bit hamming compressedsensing[C]. Proceedings of the IEEE International Symposium on Information Theory Proceedings, Istanbul, Turkey, 2013: 679-683.

[7] Laska J N, Boufounos P T, Davenport M. A, et al.. Democracy in action: Quantization, saturation compressive sensing[J]. Applied and Computational Harmonic Analysis, 2011, 31(3): 429-443.

[8] Boufounos P and Baraniuk R. 1-Bit compressive sensing[J]. Sciences and Systems, 2008: 16-21.

[9] Boufounos P. Greedy sparse signal reconstruction from sign measurements[C]. Prceedings of the Asilomar Conference on Signals Systems and Computers, Asilomar, California, 2009: 1305-1309.

[10] Laska J, Wen Z W, Yin W, et al.. Trust, but verify: fast and accurate signal recovery from 1-bit compressive measurements[J]. IEEE Transactions on Signal Processing, 2011, 59(11): 5289-5301.

[11] Jacquesy L, Laska J N, Boufounos P T, et al.. Robust 1-Bit compressive sensing via binary stable embeddings of sparse vectors[J]. IEEE Transactions on Information Theory, 2013, 59(3): 2082-2102.

[12] Sun B, Chen Q, Xu X, et al.. A fast and accurate two-stage algorithm for 1-bit compressive sensing[J]. IEICE Transactions on Information and Systems, 2013, 96(1): 120-123.

[13] 孙彪. 基于压缩感知的信号频谱测量方法研究[D]. [博士论文],华中科技大学, 2013.

Sun Biao. Research of signal spectrum measurement based on compressing senging[D]. [Ph.D. dissertation], Huazhong University of Science & Technology, 2013.

[14] Mallat S and Zhang Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.

[15] Tropp J and Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2008, 53(12): 4655-4666.

[16] Dai W and Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[C]. Proceedings of the International Symposium on Turbo Codes and Related Topics, Turbocoding, Lausanne, Switzerland, 2008: 402-407.

[17] Laska J and Baraniuk R G. Regime change: bit-depth versus measurement-rate in compressive sensing[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 3496-3505.

[18] Blumensath T and Davies M. Iterative hard thresholding for compressed sensing[J]. Applied Computational Harmonics Analysis, 2009, 27(3): 265-274.

[19] Jacques L, Degraux K, and Vleeschouwer C. Quantized iterative hard thresholding: bridging 1-bit and high-resolution quantized compressed sensing[C]. Proceedings of the 10th Sampling Theory and Application, Jacobs University, Bremen, Germany, 2013: 105-108.

[20] 段世芳, 马社祥. 变步长稀疏自适应的迭代硬阈值图像重构[J]. 计算机工程与科学, 2013, 35(8): 120-124.

Duan Shi-fang and Ma She-xiang. Variable step size sparsity adaptive iterative hard thresholding image reconstruction[J]. Computer Engineer & Science, 2013, 35(8): 120-124.

[21] Do T T, Lu Gan, and Nguyen N. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]. Proceedings of the Asilomar Conference on Signals, Systems, and Computers, California, USA, 2008: 581-587.

[22] Blumensath T and Davies M. Iterative thresholding for sparse approximations[J]. Applied Computational Harmonics Analysis, 2008, 14(5): 629-654.

[23] Yan M, Yang Y, and Osher S. Robust 1-bit compressive sensing using adaptive outlier pursuit[J]. IEEE Transactions on Signal Processing, 2012, 60(3): 3868-3875.

张京超： 男，1984年生，博士生，研究方向为压缩采样、稀疏信号处理等.

付 宁： 男，1979年生，博士，副教授，硕士生导师，研究方向为压缩采样、稀疏信号处理、自动测试技术、盲信号处理等.

杨 柳： 女，1989年生，硕士生，研究方向为压缩采样、1-Bit压缩感知等.

A Blind 1-Bit Compressive Sensing Reconstruction Method

Zhang Jing-chao Fu Ning Yang Liu
(Department of Automatic Test and Control, Harbin Institute of Technology, Harbin 150080, China)

1-Bit Compressive Sensing (CS) is an important branch of standard CS. The existing 1-Bit CS algorithm-Binary Iterative Hard Thresholding (BIHT) can perfectly recovery signals with high precision and consistency, which requires exact sparsity level in the recovery phase. Considering this problem, a new Sparsity Adaptive Binary Iterative Hard Thresholding (SABIHT) algorithm without prior information of the sparsity is proposed by modifying the BIHT algorithm. By using the adaptive process of automatically adjusting the hard threshold parameters and test conditions to estimate the sparsity, the proposed algorithm realizes accurate reconstruction and estimates the true supporting set of approximated signal. The analytical theory and simulation results show that the SABIHT algorithm recovers effectively the signals without prior information of signal sparsity and the reconstruction performance is similar to the BIHT algorithm.

Compressive Sensing (CS); 1-Bit compressive sensing; Blind Reconstruction; Binary Iterative Hard Thresholding (BIHT)

TN911.72

A

1009-5896(2015)03-0567-07

10.11999/JEIT140419

2014-03-31收到，2014-10-08改回

国家自然科学基金(61102148)和黑龙江省博士后基金(LBH-Z10167)资助课题

*通信作者：付宁 funinghit_paper@163.com