高中数学解题思想方法之一——换元法

吉林省龙井市龙井高级中学 李京玉

解数学题时，把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化，这叫换元法。换元的实质是转化，关键是构造元和设元，理论依据是等量代换，目的是变换研究对象，将问题移至新对象的知识背景中去研究，从而使非标准型问题标准化、复杂问题简单化，变得容易处理。

换元法又称辅助元素法、变量代换法。通过引进新的变量，可以把分散的条件联系起来，隐含的条件显露出来，或者把条件与结论联系起来。或者变为熟悉的形式，把复杂的计算和推证简化。

它可以化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式，在研究方程、不等式、函数、数列、三角等问题中有广泛的应用。

换元的方法有：局部换元、三角换元、均值换元等。局部换元又称整体换元，是在已知或者未知中，某个代数式几次出现，而用一个字母来代替它从而简化问题，当然有时候要通过变形才能发现。三角换元，应用于去根号，或者变换为三角形式易求时，主要利用已知代数式中与三角知识中有某点联系进行换元。我们使用换元法时，要遵循有利于运算、有利于标准化的原则，换元后要注重新变量范围的选取，一定要使新变量范围对应于原变量的取值范围，不能缩小也不能扩大。

示范性题：

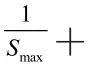
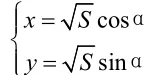
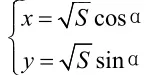
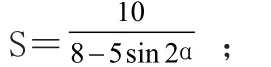
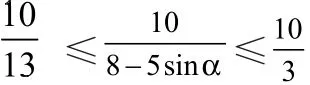
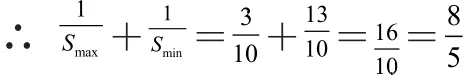
此种解法后面求S最大值和最小值，还可由的有界性而求，即解不等式：这种方法是求函数值域时经常用到的“有界法”。

【另解】 由S＝x2＋y2，设

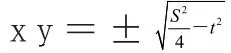
移项平方整理得 100t2+39S2－160S＋100＝0 。

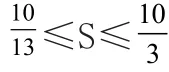
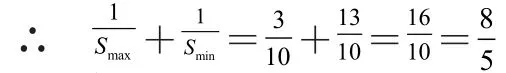
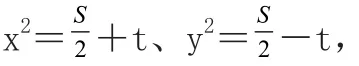
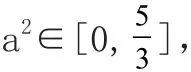
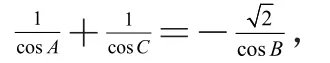
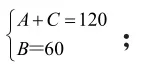
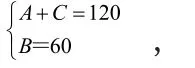
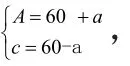
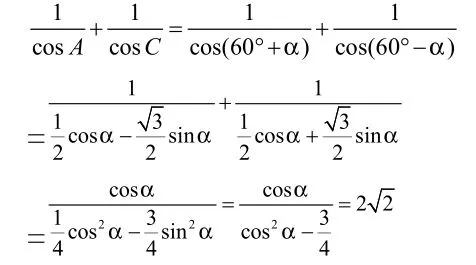
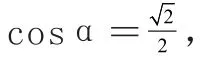
【另解】由A＋C＝2B，得A＋C＝120°，B＝60°。所以，设

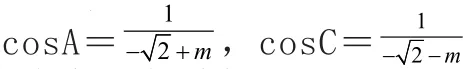
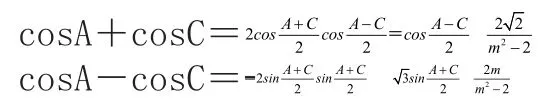
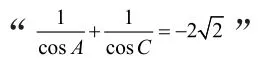
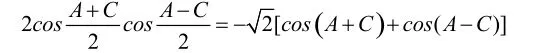
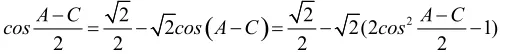
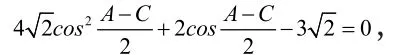
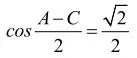
例3. 设a＞0，求f(x)＝2a(sinx＋cosx)－sinx·cosx－2a2的最大值和最小值。

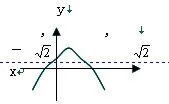
【解】 设sinx＋cosx＝t，则由(sinx＋cosx)2＝1＋2sinx·cosx得：

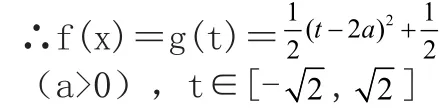
t时，取最小值：－2a2－

当2a≥时，取最大值：

当时，t＝2a，取最大值： 。

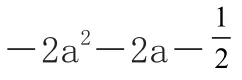
【注】 此题属于局部换元法，设sinx＋cosx＝t后，抓住sinx＋cosx与sinx·cosx的内在联系，将三角函数的值域问题转化为二次函数在闭区间上的值域问题，使得容易求解。换元过程中一定要注意新的参数的范围与sinx＋cosx对应，否则将会出错。本题解法中还包含了含参问题时分类讨论的数学思想方法，即由对称轴与闭区间的位置关系而确定参数分两种情况进行讨论。

一般地，在遇到题目已知和未知中含有sinx与cosx的和、差、积等而求三角式的最大值和最小值的题型时，即函数为f(sinx±cosx，sinxcsox)，经常用到这样设元的换元法，转化为在闭区间上的二次函数或一次函数的研究。