向量解题优越性浅议

福建省连城县第二中学 罗英平

高中数学新教材引进向量知识，它对我们解决数学中一些抽象的、复杂的、隐形的、不可测视的数学问题提供了一种便捷、好理解、易解答的良好通道，对立几的一些问题，它摆脱以往那种作、找、证、求，最后得出结论的复杂解题模式，向量给我们提供一种从简单而又程序化的运算方法来解决问题，它是一种更为直观形象的解题工具，同时它也为学生学习数学开拓了一条创新思维的好通道。下面就向量在高中数学的一些运用作一些分析浅议。

一、平几中可用向量求解直线方程及判断直线的位置关系

在平面解析几何中，直线l: Ax+ B y+ C =0（A,→B不同时为0）的方→向向量可取为v = (- B, A)，法向量n =(A , B),研究直线的位置关系，完全可用它两个向量来全权处理。况且它们的坐标值与变量x,y的系数相关，这对我们解决起问题来又方便了许多。

例1：已知点A(1,2)B(3,1) ，则线段AB的垂直平分线的方程是_______________。

解析：依题知，向量就可作为所求直线的法向量，从而方程可设为2x-y+t=0，再由直线又过线段AB的中点将之代入即可求出参数，所以中垂线方程为即4 x - 2 y -5 = 0。

二、求线段的比值

例2：如图1，在ΔABC中，D,E 分别在边BC,AB上，且满足BD=CD,BE=2AE，AD,CE相交于F，求CF：EF的值。

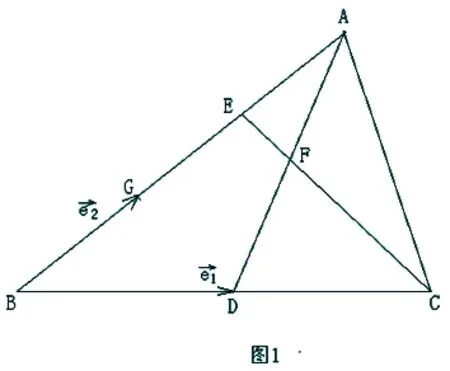
解析：本题可用初中平几的比例线段以及相似三角形的知识来求解，在学完平面向量基本定理、向量的三角形运算法则及三点共线的充要条件等相关知识后，我们也可以用它们来解该题。

三、用向量来确定点的坐标

利用向量相等的充要条件和向量坐标的确定方法，来确定相关点的坐标，可避免思维上的混乱，比较顺利地求解一些点的坐标。

例3：已知点A(2,4),B(6,-2) ，点P分有向线段的比为－2，求P的坐标。

利用向量来解题，它给我们简洁上的美好感受，但要灵活熟练利用它来解题，我们必须：①有关数学概念、数学基础知识、基本数学理论要清晰；②要清楚所用知识的理论依据；③能从题中有已知条件提炼出对解题有用的信息；④对向量的运算法则、规律要理解掌握，并能熟练进行数学运算；⑤能在思维严密、结构严谨的条件下进行有条理的计算和论证，使问题得到完美解答。

四、向量在立几中，对解决空间元素的位置关系、空间角及空间距离有很好的应用

如果用纯几何法来完成它们，有时有很大难度，甚至根本无法解，因为它们有时是隐藏的、不可视的、抽象的，有些几何量作不出，更不好证和求解了。而向量法正好可以避开这些，只要我们能从理论上理解它，运算能力强，思维严密严谨，不用作、找、证、求，即可得到完美的解决。

在立几中，直线可用其方向向量来代表，平面可用其法向量来代表，即可完成一系列的论证和求解。

设直线的方向向量为平面法向量为，则有

1.两直线平行的充要条件是或使的两直线垂直的充要条件是或

3.直线和平面平行的充分条件是或

4.直线和平面垂直的充要条件是或使的

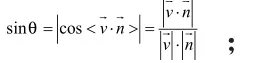
6.两平面平行的充要条件是或使的

7.两平面垂直的充要条件是或

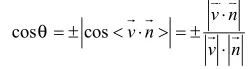
9.两异面直线的距离等于两直线上各一点P,Q的连线段表示的向量在两直线的公垂向量 上的射影长度（公垂向量即为与两异面直线都垂直的向量）,即

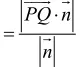
10.线到面，面到面的距离可统一归为点到面的距离，则点P到平面α的距离等于平面上任意点A与P构成的向量在平面法向量方向上的射影长度，即：

从上面的公式可知，只要相应的公式记忆清楚，公式的来源明白，解决空间元素位置、空间角及空间距离的求解完全转化两向量之间的问题了。

用向量解题，要能正确读图，建立恰当的空间直角坐标系，并能正确确定各相关点的坐标，点坐标确定正确是解题正确的前提和基础，这要求思路要清晰，知识公式要明晰，解题要素明确并能求解正确，这样才能达到解题完美。

以上是向量优越性的部分运用，当然任何方法的优劣都是相对的，只有在真正理解掌握知识的来龙去脉，方法的理论依据和形成过程，并在熟练的基础上得以灵活运用，那才能真正学好数学。学数学不难，只要有正确的做学问的态度，肯下功夫，有持之以恒的毅力，有严密训练，数学逻辑思维能力，运算能力，表达能力，空间想象能力等数学能力都能得到提高和发展，在熟的基础上就能生巧，就能形成严谨的、完善的知识结构网络，并能在运用上得心应手。