三次函数

冯广东

摘 要：近三年新课标全国Ⅱ卷中三次函数出现了两次.2013年文科第11题与理科第10题为同一题目，其中涉及到一个冷门：三次函数的对称中心；2014年文科第21题纯粹考查三次函数。看来在高考中，尤其是文科数学中对导数的考查，三次函数是一个不错的载体。在我们的文科数学课本选修1-1中，也大量的以三次函数为载体对导数的应用进行训练，大小共出现了二十三题次。但这些训练都是最基础的，不足以应对高考的压轴题。那么就应该把三次函数给学生做一个系统的归纳和适当的拓展。

关键词：三次函数 极值 单调性 零点 对称性

中图分类号：G634 文献标识码：A 文章编号：1672-3791（2015）02（a）-0250-02

1 背景

内蒙古自治区实施新课标以来，至今经历了三次高考。该区所用的新课标全国Ⅱ卷中，三次函数出现了两次。2013年文科第11题与理科第10题为同一题目，其中涉及到一个冷门：三次函数的对称中心；2014年文科第21题纯粹考查三次函数。看来在高考中，尤其是文科数学中对导数的考查，三次函数是一个不错的载体。在文科数学课本选修1-1中，也大量的以三次函数为载体对导数的应用进行训练，大小共出现了二十三题次。但这些训练都是最基础的，不足以应对高考的压轴题。那么我们就应该把三次函数给学生做一个系统的归纳和适当的拓展。

2 准备

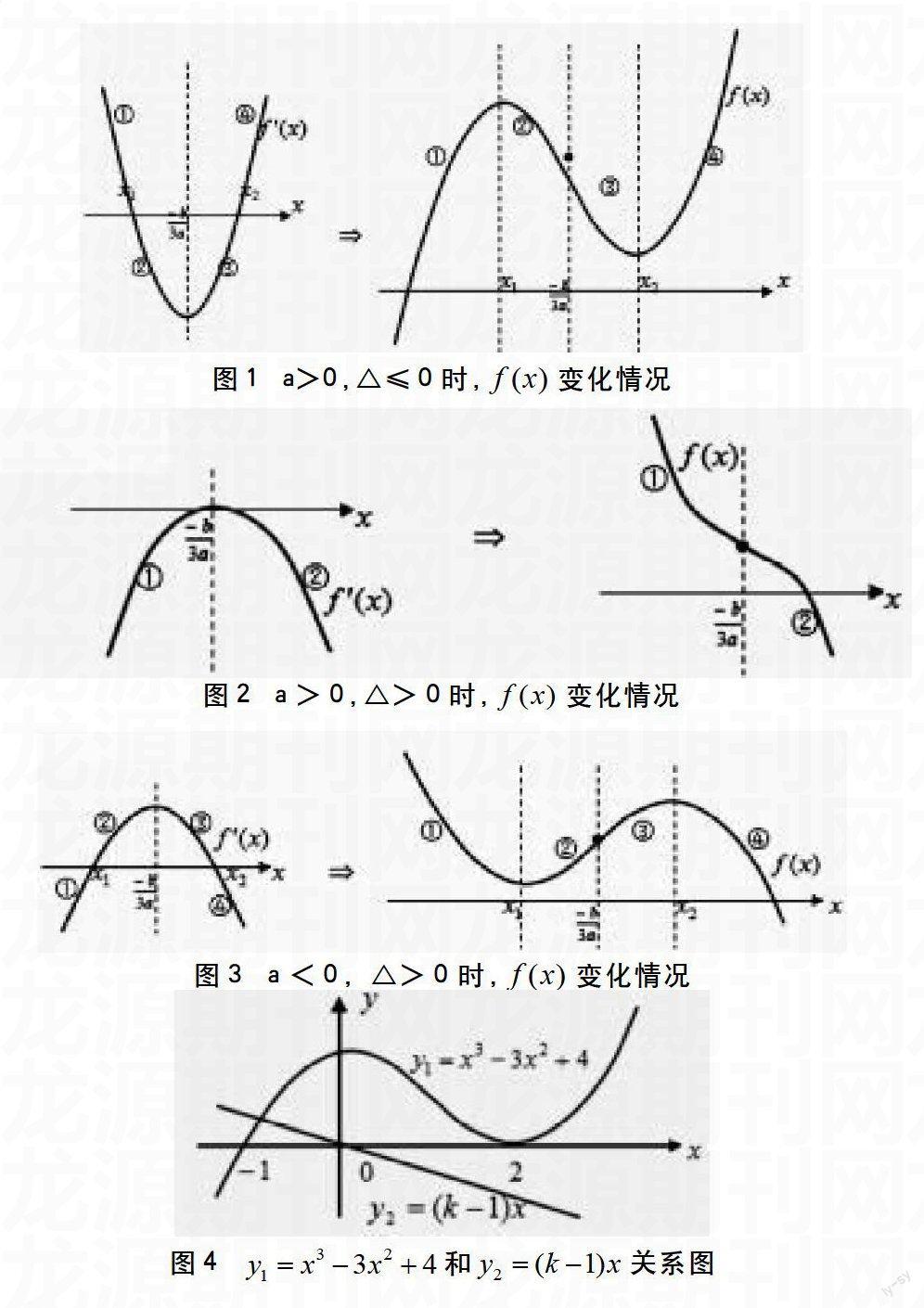
学生先需要知道、掌握以下知识，（1）零点；（2）导数与极值；（3）导数与单调性；（4）导数与原函数图象陡、缓的关系：无论递增还是递减，逐渐增大，的图象就由缓平逐渐陡直；反之，逐渐减小，的图象就由陡直逐渐缓平。

3 探究

（2）若，同理可得，的图象。

时如图3所示。把上面两种时的图象逐渐向下平移，连同上图，各自零点个数的变化都依次为：“一个、二个、三个、二个、一个”五种情况（图略）。显然：一个零点（极值同号）、两个零点（一个极值为0）、三个零点（极值异号）。

4 结语

由上面的图象可以直观的看出三次函数的一些性质：

（1）极值、单调性：略。

（2）零点的个数：

①或时，一个零点；

②时，两个零点；

③时，三个零点。

（3）对称性：看的图象可知，图象的变化规律在的两侧恰好相反，再结合图象本身的特征，不难看出：的图象关于点对称。

下面给出这一定理的严格证明：

假设函数的对称中心为，则将函数的图象按向量平移后得到函数为奇函数。

綜上，在上有唯一实根。即，当时，曲线与直线只有一个交点。

点评：以上解答，主要受转化以后的图象启发而得。

纵观以上实例，只要深刻掌握三次函数的图象特征和性质，就能找到明确的解题思路、拓宽解题思路。有助于提高我们对知识系统性的认识和理解水平。

参考文献

[1] 徐建君.三次函数的对称中心及其应用[J].考试（高考.物理版），2006（11）：17-19.

[2] 内蒙古教育招生考试中心.2014年普通高等学校招生全国统一考试文科数学答案[Z].