水环境突发事件下的群体行为系统动力学模拟*

2015-07-02宋红玉

学海 2015年4期

宋红玉

宋红玉

本文在理论分析的基础上，基于SIR模型拓展构建了水环境突发事件下谣言传播群体行为的系统动力学模型，并以太湖蓝藻事件为例，运用Vensim软件进行了模拟仿真，同时通过改变系统各参数的取值研究了各参数的影响作用。理论研究部分认为：突发事件下个体的负面情绪及行为反应由于受从众效应的影响表现出群体性特征，水环境突发事件下群体行为的具体表现包括抢购、谣言传播和逃离事发区，就谣言传播群体行为而言，影响因素包括客观因素和主观因素两方面。模拟仿真部分得出的启示是：可以从系统各参数入手来预防和治理水环境突发事件下的谣言传播群体行为。

水环境突发事件群体行为谣言传播 SIR模型系统动力学

2014年4-5月接连发生的兰州、武汉、靖江饮用水危机造成很大社会反响。实际上，近些年我国已发生多起水环境突发事件，如2013年7月广西贺江的水体重金属污染，2007年5月的太湖蓝藻事件以及2005年11月的松花江重大水污染事件等。这些事件的发生均给当地民众的生产、生活带来严重影响，并威胁到人们的身体健康、社会的和谐稳定。就心理层面来说，由于个体在水环境突发事件中的负面情绪及行为反应受多种因素影响，其中从众效应的影响极为突出，从而使得个体的情绪与行为反应表现出群体性特征。因此，研究水环境突发事件下的群体情绪及行为反应有着重要的现实意义。

在群体负面情绪的研究方面，李从东等(2013)①运用系统动力学方法将群体负面情绪分为个体、社会和治理三个层面，分析了每个层面的行为模式和关键变量，并选取某公司生产车间进行动态仿真，发现个体认知水平和预警机制在其中发挥着显著作用；王雷等(2014)②在充分考虑群体情绪传播的动力学机制和社会网络成员间亲密、信任关系及权重的基础上，建立了群体情绪传播模型，并将仿真结果与心理学实验结果比对，比对结果表明该模型具有较高的生态效度。而突发事件下的群体行为研究主要以逃逸行为、谣言传播等为研究对象，逃逸行为研究如Ebihara(1992)③的紧急疏散行为仿真模型研究、Saloma(2003)④的恐慌逃逸中自组织队列和自由规模行为研究等；谣言传播研究大多借鉴传染病模型展开，如Sudbury(1985)⑤采用SIR模型研究了谣言在小世界网络中的传播规律，结论是当系统中人口数量趋于无穷大时，从未听过谣言的人群比例约为20.3%，孙多勇(2005)⑥、佘廉、沈照磊(2011)⑦建立了基于传染病SIR模型的突发事件谣言传播模型，赵玉忠、陈业华(2012)⑧比较了不同参数值下S、I、R随时间变化而变化的具体数值、提出了减少和预防突发事件下谣言传播的相应策略，霍良安(2012)⑨基于信息传播中不同受众间存在竞争的思想建立了不实信息传播动力学模型并进行了分析。

综合上述分析发现，就谣言传播群体行为而言，以往的研究主要是通过构建模型进行理论分析，运用案例数据仿真模拟的较少。本文将在理论研究的基础上，基于不同受众在信息传播中相互竞争的思想，运用系统动力学方法、采用Vensim软件绘制系统流图，建立水环境突发事件下的谣言传播模型，并根据已有文献及太湖蓝藻事件回溯性调查数据设定系统参数值，进行模拟仿真。

水环境突发事件下群体行为的理论分析

(一)水环境突发事件下群体行为的具体表现

水是生命之源，水环境突发事件的发生严重影响当地民众的生产生活、威胁人们的身体健康，因此面对突如其来的供水危机民众可能会恐慌、焦虑甚至愤怒。为了控制内心的情绪、努力恢复心理上的平衡，人们开始行动。模仿理论认为，突发事件下多数个体有意识的人格会丧失，取而代之的是无意识的人格，此时个体本能地通过模仿力求保持与周围多数人行为一致；感染理论也认为，情绪感染以及暗示的影响，使得人们的心理朝着某一方向发展并有将暗示观念立即转化为行动的倾向。也就是说，在水环境突发事件下，从众心理使得个体的行为更多地表现出群体性特征。

水环境突发事件下群体行为的具体表现有：(1)抢购。抢购是个体自保的一种反应。在水环境突发事件中，突然出现的水危机严重影响居民的正常生活，因此为了解决生活问题，居民开始采购矿泉水及食品，但很快居民的个人行为转变为群体行为，采购发展为抢购，群体的抢购引发矿泉水脱销、矿泉水价格上涨等次生事件，这反过来又加剧了民众的恐慌和社会的不稳定；(2)谣言传播。有研究表明，听信并传播谣言是个体克服恐惧的一种方法。因此，在水环境突发事件下，急于了解情况的民众如果无法从正式信息渠道获得官方消息，则会通过人际关系等非正式渠道获取小道消息并加以传播，即谣言的传播。在谣言传播过程中，由于加入了传播者的主观理解，可能会夸大或歪曲所传播信息，从而引起社会范围内更大程度的恐慌；(3)逃离事发区。在水环境突发事件下，有条件的民众可能选择离开事发地以躲避水荒，在从众心理的作用下，这一行为可能发展为群体行为。

(二)水环境突发事件下谣言传播群体行为的影响因素

1.关于谣言的定义

2.水环境突发事件下谣言传播的影响因素分析

(1)客观因素

客观因素包括事件的重要性和事件的模糊性。发生的事件越重要、事件的相关信息越缺乏，则谣言越可能产生。水环境突发事件下，由于事件的发生严重威胁当地民众的用水安全，影响人们的日常生活，因此备受关注。然而，在事件发生初期，一方面民众急于了解事件发生的来龙去脉及进展情况，另一方面政府部门及媒体无暇应对复杂的头绪，未能及时披露相关信息，在一时无法弄清事实真相的情况下，各种谣言就会出现。

(2)主观因素

除了上述客观因素外，谣言传播中主观因素也很重要。这里的主观因素是指传播谣言人的批判能力，即对谣言的识别能力。传播者对谣言的识别能力越强，就越可能对谣言免疫，谣言传播就越会减弱，直至消亡；反之，谣言则会被广泛传播。传播者对谣言的识别能力取决于个体自身的素养，包括知识水平、社会经验、个性特点、对事件的了解程度等。个体的科学文化素养越高，对谣言的识别能力可能就越强，从而越不可能轻易听信和传播谣言。

水环境突发事件下谣言传播的系统动力学建模

现有的谣言传播模型大多借鉴传染病SIR模型构建。SIR模型将人群分为易感染者S、已感染者I和治愈者或移出者R三类，在不考虑生死和迁移的情况下，SIR模型的传染机理是S→I→R。但基于第二部分的理论分析，如果考虑到谣言传播中存在受众间的作用关系，则谣言传播机理要比SIR模型复杂，因此需要在SIR模型基础上进行拓展以构建谣言传播模型。下面作详细讨论。

(一)模型的基本架构

本文将系统中的人群分为两大类：一类是有限理性人群X，另一类是理性人群Y。有限理性人群X包括易感人群S和传播人群I，易感人群S是指缺乏辨识能力、容易轻信谣言的人群，传播人群I指已接受谣言并进行传播的人群；理性人群Y是指具有辨识能力、不相信谣言的人群，该人群对易感人群S进行科普教育、对传播人群I进行教导，帮助他们认清事实的真相。因此，模型的基本架构由易感人群S、传播人群I和理性人群Y三部分组成。

(二)模型的基本假设

第一，不考虑人口的生死、迁移等种群动力因素。如果用S(t)、I(t)和Y(t)分别表示t时刻易感人群、传播人群和理性人群的数量，N表示系统中的总人口数，则有S(t)+I(t)+Y(t)=N，而N≡常数，记为K；

第二，不考虑系统内成员因对事件失去兴趣而退出系统的情形；

第三，线性关系假定，即：t时刻单位时间内一个传播者I传染易感者S的数目与该时刻易感者人数S(t)成正比，t时刻单位时间内一个理性者Y成功说服易感者S的数目与该时刻易感者人数S(t)成正比，t时刻单位时间内一个理性者Y成功说服传播者I的数目与该时刻传播者人数I(t)成正比；

第四，不考虑各系数值在事件发展不同阶段变化的情形。如果用a、b、c分别表示I-S、Y-S和Y-I之间的日接触率，用β、δ、ζ分别表示I-S接触后的传染率、Y-S接触后的成功说服率和Y-I接触后的成功说服率，则t时刻单位时间内被传播并相信谣言的人数、易染者S中被成功说服的人数和传播者I中被成功说服的人数分别为aβI(t)S(t)、bδY(t)S(t)和cζY(t)I(t)，假定a、b、c、β、δ、ζ的值在整个事件发展过程中保持不变。

(三)模型的建立

本文运用系统动力学Vensim软件绘制出水环境突发事件下谣言传播的系统流程图，如图1所示。具体内容为：

第一，t时刻单位时间内易染者S数量的变化表现为易染者转变为传播者和易染者转变为理性者两种情况引起的易染者数量减少，即-[aβI(t)S(t)+bδY(t)S(t)]；

第二，t时刻单位时间内传播者I数量的变化表现为易染者转变为传播者引起的传播者数量增加和传播者转变为理性者导致的传播者数量减少，即aβI(t)S(t)-cζY(t)I(t)；

第三，t时刻单位时间内理性者Y数量的变化表现为易染者转变为理性者和传播者转变为理性者两种情况引起的理性者数量增加，即bδY(t)S(t)+cζY(t)I(t)。

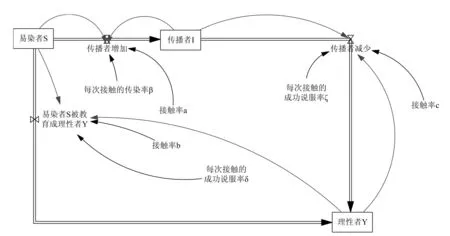
图1 水环境突发事件下谣言传播的系统流程图模拟仿真及结果分析

本文以太湖蓝藻事件为例进行水环境突发事件下谣言传播的系统动力学模拟仿真。

(一)参数值的设定

1.N、S(0)、I(0)和Y(0)的设定

根据太湖蓝藻事件发生当年的无锡市统计年鉴，当时无锡市总人口为461.74万人，其中江阴市119.61万人、宜兴市125.81万人、其他7个区共计216.32万人。本文采取数据缩放的方法，将系统中的总人数N设定为1000人。

S(0)、I(0)和Y(0)根据调研数据适当调整后确定。本研究对经历太湖蓝藻事件的无锡市市民进行了回溯式问卷调查，调查选取无锡市若干小区、大型广场、购物中心、污染企业、相关职能部门和人流量较大的路口进行，范围涵盖除江阴市、宜兴市之外的其他7个区，共计发放800份问卷，回收766份，剔除缺失值后最终得到231个有效样本。考察被调查者在事件发生初期相关知识水平的题项包括：“蓝藻爆发时，您对蓝藻及其危害了解吗？”、“蓝藻事件发生前，您对水环境污染等方面的信息了解得多吗？”、“蓝藻事件发生初期，您对该事件的来龙去脉了解吗？”，均采用五级李克特量表形式，从“很不了解”到“很了解”分5个等级分别赋予1-5的分值。231个有效样本中有4个样本3个题项的得分均为4或5，占总样本数的1.73%，又考虑到事件发生初期官方信息缺乏、专家忙于研究和攻关无暇顾及其他，因此，本文在调研数据基础上作适当调整，将系统中理性人群的初始比例设定为1%，即Y(0)=10。同样的办法，本文将系统中谣言传播者的初始比例也设定为1%，即I(0)=10。这样，S(0)=980，占系统总人数的98%。

2.系数a、b、c、β、δ和ζ值的设定

β指I-S接触后的传染概率，它取决于谣言传播时有多少个易染者相信。本文通过询问“蓝藻爆发时，周围人群的紧张行为对您影响大吗？”，采用五级李克特量表形式，从“没有影响”到“影响很大”分5个等级分别赋予1-5的分值，来考察被调查者的从众心理。调查结果显示，231个有效样本中有63.2%的样本取值为3-5，这说明蓝藻爆发时有63.2%的被调查者不同程度地受到周围人群紧张行为影响。一般认为，从众心理越强烈，则越易听信谣言，因此，本文在对上述数据作适当调整后将传染率β设定为60%，也即β=0.6。

b指Y-S的日接触率，它取决于1个理性者平均每天接触多少个易染者。考虑到事件发生初期权威信息缺乏等因素，本文将理性者平均每天接触的易染者人数设定为4人，略低于传播者接触的数量，此时b=0.004。

δ指Y-S接触后易染者S被成功说服的概率，它取决于理性者接触易染者后有多少人被说服。根据前述的数据设定，谣言传播时有60%的易染者相信并进行传播，也即其余的40%不相信谣言，假定这其中有20%被理性者成功说服，则δ=0.2。

c指Y-I的日接触率，它取决于1个理性者平均每天接触多少个传播者。假定1个理性者平均每天接触0.3个传播者，在事件发生初期，传播者人数为10人，0.3/10=0.03，则c=0.03。

ζ指Y-I接触后传播者I被成功说服的概率。考虑到传播者I与易染者S相比，通常思想较为顽固、更难说服教育，因此ζ值应低于δ值，本文将ζ设定为10%，也即ζ=0.1。

(二)运行结果

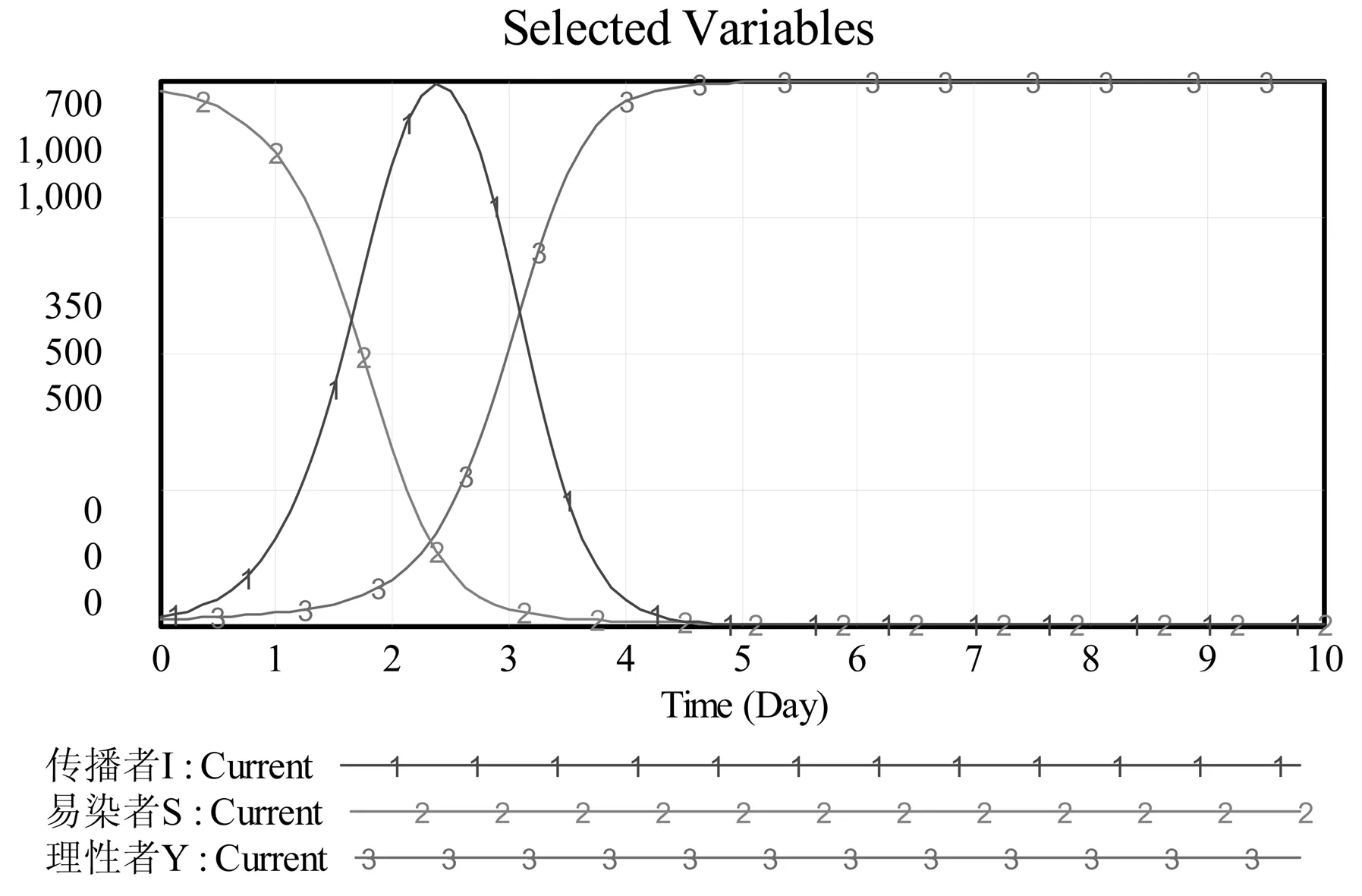
图2 太湖蓝藻事件下谣言传播模拟仿真图表1 太湖蓝藻事件下谣言传播模拟仿真参数数据表

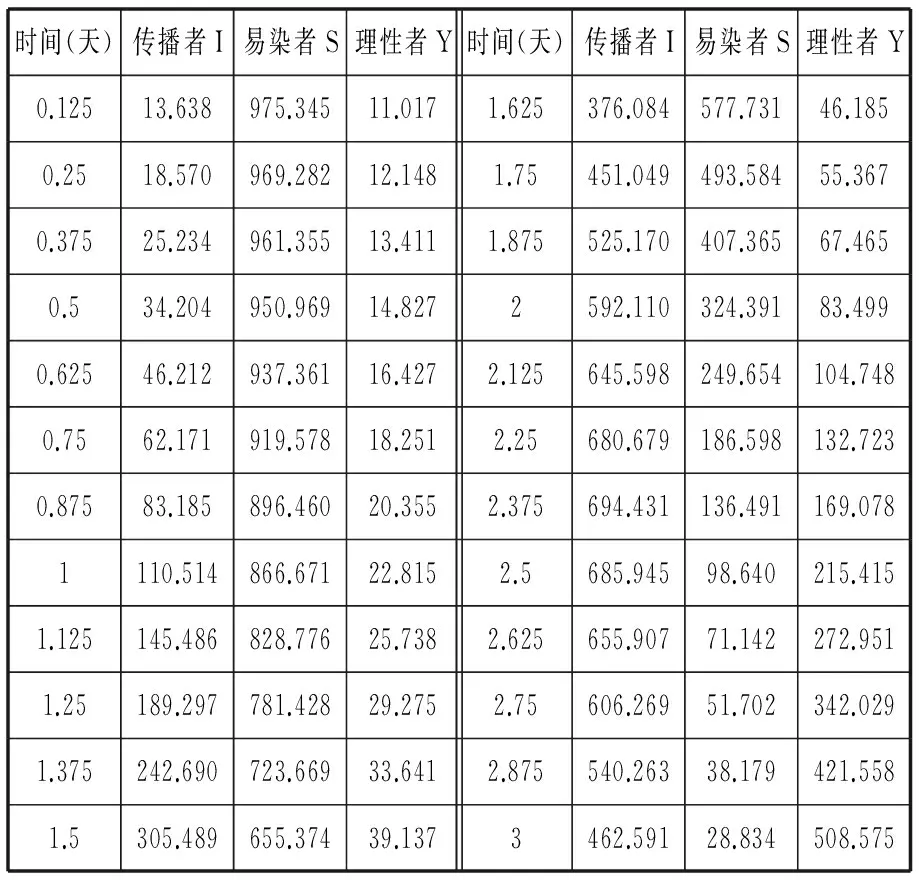
时间(天)传播者I易染者S理性者Y时间(天)传播者I易染者S理性者Y0.12513.638975.34511.0171.625376.084577.73146.1850.2518.570969.28212.1481.75451.049493.58455.3670.37525.234961.35513.4111.875525.170407.36567.4650.534.204950.96914.8272592.110324.39183.4990.62546.212937.36116.4272.125645.598249.654104.7480.7562.171919.57818.2512.25680.679186.598132.7230.87583.185896.46020.3552.375694.431136.491169.0781110.514866.67122.8152.5685.94598.640215.4151.125145.486828.77625.7382.625655.90771.142272.9511.25189.297781.42829.2752.75606.26951.702342.0291.375242.690723.66933.6412.875540.26338.179421.5581.5305.489655.37439.1373462.59128.834508.575

(三)结果分析

表1显示，在2.375天时传播者人数达到最大值694人，而在此之前的1.875天，传播者人数已达到525人，超过系统总人数的一半。这说明此时形势较危急，整个社会处于小道消息横行、恐慌情绪蔓延的境地。2.375天后传播者人数开始下降，到第3天下降至500人以下，此时理性者人数开始超过500人。此后，随着时间的推移，到第5天时传播者消失，第6天易染者消失，至此谣言传播过程结束，太湖蓝藻事件也相应进入逐渐平息的阶段。

应该看到，在此事件中谣言传播历经了产生、成长、高潮、衰退直至消亡的所有阶段。一开始，事态的发展非常迅速，很快谣言传播者超过系统总人数的一半，直至达到接近700人的最大值。此时形势非常严峻，如果当地政府不能采取有效措施解决危机、疏导民众情绪、做教育说服工作，则很容易引发社会骚乱。这种状况的形成与系统中各参数的取值有直接关系，因此可以考虑从这几方面着手进行谣言传播的预防与治理。下面本文对各参数的影响作用展开具体讨论。

1.初始I和Y

在本案例中，I和Y的初始值均设定为10人，如果I(0)减少至1人，Y(0)不变，则S(0)=989人；或者Y(0)增加至30人，I(0)不变，则S(0)=960人，假定两种情况下其余参数值均不变，则谣言传播的演化发展情况分别如图3和图4所示。

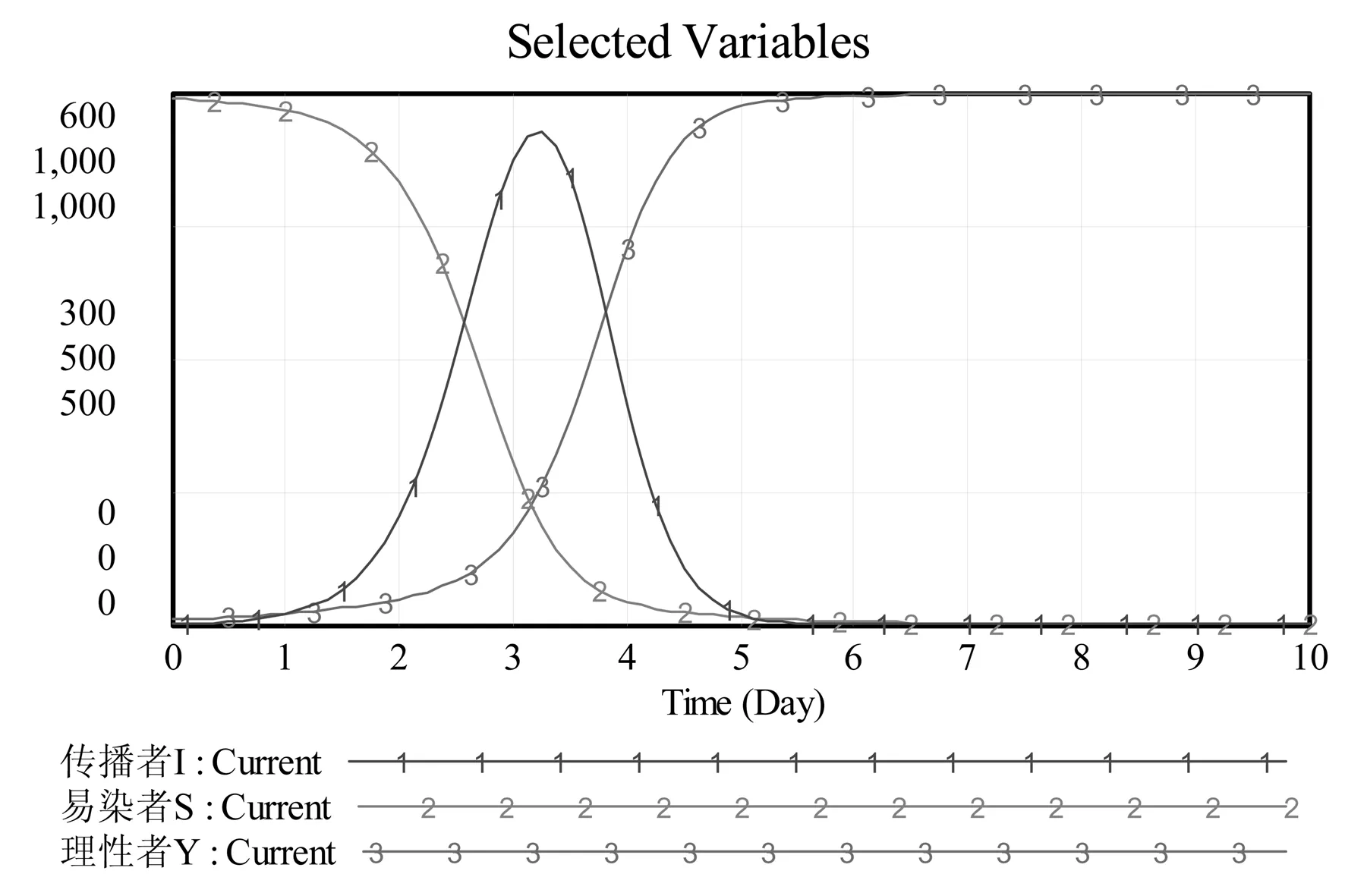
图3 I(0)=1的谣言传播模拟仿真图

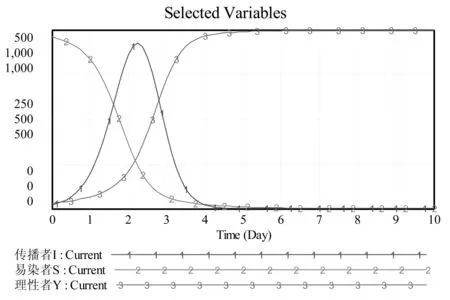
图4 Y(0)=30的谣言传播模拟仿真图

从图3中看出，如果I(0)=1，则事态发展较为缓慢，至3.25天时传播者人数达到最大值556人；从图4中看出，如果Y(0)=30，则传播者人数始终未超过系统总人数的一半，事件中谣言和非理性情绪一直未占据主导地位，整个社会较为理性、平和，没有出现极端情况。因此，可以通过减少初始传播者人数、增加初始理性者人数来防治谣言传播群体行为的发生。

2.接触率a、b、c

在本案例中，I-S的日接触率a设定为0.005，Y-S的日接触率b设定为0.004，Y-I的日接触率c设定为0.03。如果接触率a降低至0.002，或者接触率b提高至0.01，又或者接触率c提高至0.1，同时假设三种情况下其余参数值均保持不变，则谣言传播的演化发展情况如图5、图6和图7所示。

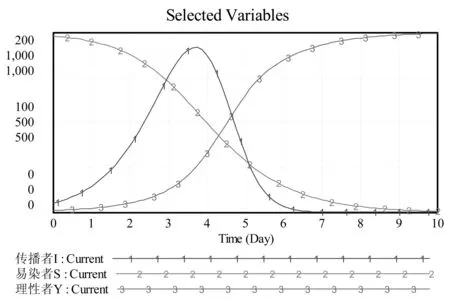
图5 a=0.002的谣言传播模拟仿真图

图6 b=0.01的谣言传播模拟仿真图

从图中看出，如果a=0.002，则事态发展较为平缓，至3.75天时传播者人数达到最大值183人；如果b=0.01，则虽然事态发展较为迅速，但传播者人数始终未达到系统总人数的一半，在第2天时达到最大值381人；如果c=0.1，则传播者人数在1.875天时达到最大值402人。因此，通过降低I-S接触率、提高Y-S接触率和Y-I接触率，可以避免或减轻水环境突发事件下的谣言传播群体行为。

图7 c=0.1的谣言传播模拟仿真图

3.传染率β、成功说服率δ和ζ

在本案例中，I-S接触后的传染概率β设定为0.6，Y-S接触后易染者被成功说服的概率δ设定为0.2，Y-I接触后传播者被成功说服的概率ζ设定为0.1。如果传染率β降低至0.3，或者成功说服率δ提高至0.4，又或者成功说服率ζ提高至0.2，同时假设三种情况下其余参数值均保持不变，则谣言传播的演化发展情况如图8、图9和图10所示。

图8 β=0.3的谣言传播模拟仿真图

从图中看出，如果β=0.3，则事态发展较缓慢，至3.5天时传播者人数达到最大值292人；如果δ=0.4，则事态发展较均衡，成长和衰退速度相当，传播者人数在2.125天时达到最大值483人，4.5天时减少至0；如果ζ=0.2，则传播者人数在2.125天时达到最大值488人，此后衰退速度较快，至3.25天时传播者消失。因此，通过降低I-S接触后的传染概率、提高Y-S接触和Y-I接触后的成功说服率，可以避免和减轻水环境突发事件下的谣言传播群体行为。

图9 δ=0.4的谣言传播模拟仿真图

图10 ζ=0.2的谣言传播模拟仿真图

基本结论与启示

突发事件下个体的负面情绪及行为反应由于受从众效应的影响表现出群体性特征。水环境突发事件下群体行为的具体表现包括抢购、谣言传播和逃离事发区。就谣言传播而言，本文认为水环境突发事件下谣言传播的影响因素有客观因素和主观因素两方面：客观因素包括事件的重要性和事件的模糊性，主观因素是指谣言传播者对谣言的识别能力。事件越重要、信息越模糊、传播者对谣言的识别能力越弱，则谣言越易传播；反之亦然。因此，基于上述的理论分析，本文在SIR模型基础上拓展构建了水环境突发事件下谣言传播群体行为的系统动力学模型，并以太湖蓝藻事件为例，运用Vensim软件进行了模拟仿真，同时通过改变系统各参数的取值研究了各参数的影响作用。

基于各参数的影响作用，预防和治理水环境突发事件下谣言传播的群体行为可以从以下方面着手：减少初始传播者人数、增加初始理性者人数，降低I-S接触率a、提高Y-S接触率b和Y-I接触率c，降低I-S接触后的传染概率β、提高Y-S接触后的成功说服率δ和Y-I接触后的成功说服率ζ。要想达到上述目的，需要采取以下措施：(1)在水环境突发事件发生当时，政府部门应快速作出反应，迅速采取行动应对水危机，尽可能将事态影响减至最小，从而减少谣言传播者的初始人数；(2)在水环境突发事件发生之初，政府部门应第一时间发布权威信息，对事件作出解释与说明，并及时通报事件的进展情况，从而降低I-S接触率、提高Y-S接触率和Y-I接触率；(3)政府部门平时要注重加强对民众的宣传教育，普及水环境污染防治知识及相关的科学知识，提高民众的科学文化素养、知识水平和危机应对能力，从而增加理性者的初始人数、降低I-S接触后的传染概率、提高Y-S和Y-I接触后的成功说服率。

①李从东等：《基于系统动力学的群体负面情绪动力机制研究》，《情报杂志》2013年第5期。

②王雷等：《基于系统动力学的群体情绪传播模型》，《心理科学》2014年第3期。

③Ebihara M. et al. A Model for Simulating Human Behavior During Emergency Evacuation Based on Classificatory Reasoning and Certainty Value Handing，Computer-aidedCivilandInfrastructureEngineering, 1992(1).

④Saloma et al. Self-organized Queuing and Scale-free Behavior in Real Escape Panic，ProceedingsoftheNationalAcademyofSciencesofUSA, 2003 (21).

⑤Sudbury A. The Proportion of the Population Never Hearing a Rumour，JournalofAppliedProbability, 1985(22).