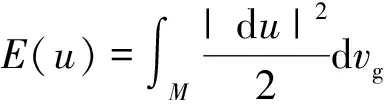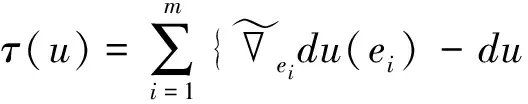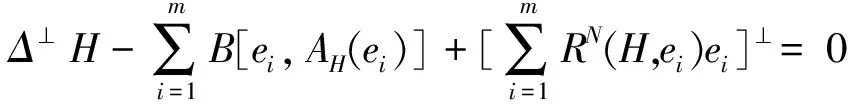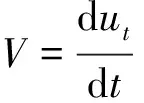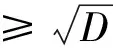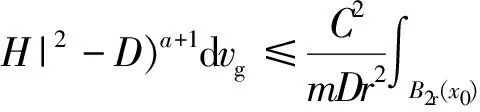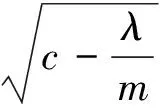具有有界曲率的黎曼流形上的双调和子流形

冯书香，方联银，李 静

(信阳师范学院 数学与信息科学学院，河南 信阳464000)

具有有界曲率的黎曼流形上的双调和子流形

冯书香，方联银，李 静

(信阳师范学院 数学与信息科学学院，河南 信阳464000)

利用分部积分法，对截面曲率上界为非负常数的黎曼流形中的完备双调和子流形进行研究。截面曲率上界为非负常数的黎曼流形中的完备双极小子流形，若子流形平均曲率积分满足某种增长性条件时，双调和子流形平均曲率是常数。特别地，单位球面中平均曲率下界为1的完备双调和子流形，若平均曲率积分满足该增长性条件时，则它的平均曲率是1。因而对BMO猜想和S.Meata猜想作出部分肯定的回答。

双调和映照；双调和子流形；双极小子流形

之后又有很多球面中双调和子流形的研究成果[3-11]。有趣的是这些例子及分类得到的结果都说明：球面中的双调和子流形具有常平均曲率。在此基础上，Balmus 和Oniciuc提出了如下猜想：

BMO猜想[6]球面中的双调和子流形都具有常平均曲率。

对于BMO猜想可以肯定的回答，若M满足下面任一条件：

(i)一个紧致的平均曲率向量恒不为零的超曲面，且|B|2≥m或|B|2≤m，其中|B|2是第二基本形式范数模长的平方[3,9]。

(ii)一个可定向的Dupin超曲面[3]。

但BMO猜想中并没有假设子流形是完备的，从某种意义上说是局部几何学中的一个问题。因此S. Meata提出了猜想，并给出了相应的定理。

S. Meata猜想[10]球面中的完备双调和子流形都具有常平均曲率。

定理1[10]设M是单位球面中平均曲率下界为1的完备双调和子流形，且

∫M(|H|2-1)pdvg<∞，(0

则M平均曲率恒为1。

本文主要对BMO、S. Meata猜想作出部分肯定的回答。在给出定理之前，先介绍几个概念。

J.Eells等人[1]提出双能量函数E2(u)=

N[X,Y]是N上的曲率算子。

定义2 设u:(M,g)→(N,h)是从m维黎曼流形(M,g)到n维黎曼流形(N,h)的映射。若双张量场τ2(u)=0，则映照u:(M,g)→(N,h)称为双调和映照。

设u:(M,g)→(N,h=〈.，.〉)是从m维黎曼流形(M,g)到m+t维黎曼流形(N,h)的一个等距浸入。对于任一点x∈M，du(X)由X确定。 〈.，.〉表示u-1h上的内积。Gauss公式为

NXY=XY+B(X,Y),X,Y∈Γ(TM),

其中B是M在N中的第二基本形式。Weingarten公式为

其中Aξ是M上单位法向量场ξ的形状算子，⊥表示M法丛上的法联络。对于任一点x∈M，点x处M的平均曲率向量为B(ei,ei)。

定义3 若等距映射u:(M,g)→(N,h)是双调和的，则M称为N的双调和子流形。

注意到u的张量场τ(u)，记作τ(u)=mH，其中H表示M的平均曲率向量。M是N中双调和子流形的充要条件为

(1)

(2)

Trg(,其中是由法联络⊥导出的Laplace算子。

(3)

下面是本文的主要结论及证明。

证明 由(3)式可得，

Δ(|H|2-D)=2|⊥H|2+

2〈B(AH(ei),ei),H〉-

2〈RN(H，ei)ei,H〉+2λ|H|2=

2〈RN(H，ei)ei,H〉+2λ|H|2≥

2mc|H|2+2λ|H|2=

2mD(|H|2-D)

(4)

其中不等号是由N的截面曲率上界为非负常数c及|AH|2≥m|H|4得出。

对于固定的一点x∈M以及r>0，在M上考虑如下截断函数：

(5)

其中Br(x0)={x∈M:d(x,x0)

-∫M[μ2(|H|2-D)a](|H|2-D)dvg=

∫Mμ2(|H|2-D)a△(|H|2-D)dvg≥

2∫Mμ2(|H|2-D)a|⊥H|2dvg+

2m∫Mμ2(|H|2-D)a+2dvg+

2mD∫Mμ2(|H|2-D)a+1dvg

(6)

另一方面，有-∫M[μ2(|H|2-D)a](|H|2-D)dvg=

-4∫Mμ(|H|2-D)aμ〈⊥H,H〉dvg-

4a∫Mμ2(|H|2-D)a-1〈⊥H,H〉2dvg≤

-4∫Mμ(|H|2-D)aμ〈⊥H,H〉dvg=

-4∫Mμ(|H|2-D)a

(7)

其中X∈Γ(TM)是单位矢量场。由(6)式，(7)式可得，

2∫Mμ2(|H|2-D)a|⊥H|2dvg+

2m∫Mμ2(|H|2-D)a+2dvg+

2mD∫Mμ2(|H|2-D)a+1dvg≤

-4∫Mμ(|H|2-D)a

-2∫Mμ2(|H|2-D)a|⊥H|2dvg+

2∫M|μ|2(|H|2-D)a+1dvg故有

∫Mμ2(|H|2-D)a+1dvg≤

(8)

由定理2可得如下推论：

推论1 设(M,g)是单位球面中平均曲率下界为1的完备双调和子流形。若

∫Br(x0)(|H|2-1)a+1dvg(a≥0)

至多以r的多项式增长，则平均曲率是1。

[1]J. Eells, L. Lemaire. Selected Topics in Biharmonic Maps[M]. CBMS: Amer. Math. Soc., 1983.

[2] G. Y. Jiang. 2-harmonic maps and their first and second variational formulas[J]. The English Translation Note di Mathematica, 2009, 28 : 209-232.

[3] A. Balmus, S. Montaldo, C. Oniciuc. New results toward the classification of biharmonic submanifolds in Sn[J]. An. Stint. Univ. Ovidius Constanta Ser. Mat., 2012, 20 : 89-144.

[4] A. Balmus, S. Montaldo, C. Oniciuc. Biharmonic PNMC submanifolds in spheres[J]. Arc.math., 2013, 51 : 197-221.

[5] A.Balmus, S. Montaldo, C. Oniciuc. Properties of biharmonic submanifolds in spheres[J]. J. Geom. Symmetry Phys., 2010, 17 : 87-102.

[6] A. Balmus, S. Montaldo, C. Oniciuc. Classification results for biharmonic submanifolds in spheres[J]. Israel J.Math., 2008,168 : 201-220.

[7] A. Balmus, C. Oniciuc. Biharmonic submanifolds with parallel mean curvature vector field in spheres[J]. J. Math. Anal. Appl., 2012, 386 : 619-630.

[8] R. Caddeo, S. Montaldo, C. Oniciuc. Biharmonic submanifolds in spheres[J]. Israel J. Math., 2002, 130 : 109-123.

[9] J. H. Chen. Compact 2-biharmonic hypersurfaces in Sn+1(1)[J]. Acta. Math. Sinica, 1993, 36 : 49-56.

[10] S. Maeta. Biharmonic submanifolds in manifolds with bounded curvature[EB/OL]. (2014-11-11)[2015-04-07] http://arxiv.org/pdf/1405.5947.pdf.

[11] X. F. Wang, L. Wu. Proper biharmonic submanifolds in a sphere[J]. Acta. Math., Sin. (Engl. Ser), 2012, 28 : 205-218.

[12] S. Maeta, H. Urakawa. Biharmonic Lagrangian submanifolds in Kalher manifolds Glasg[J]. Math. J.,2013, 55 : 465-480.

[13] E. Loubeau, S. Montaldo. Biminimal immersion[J]. Proc. Edinb. Math. Soc., 2008, 51 : 421-437.

On Biharmonic Submanifolds in Riemannian Manifold with Bounded Curvature

FENG Shu-xiang, FANG Lian-yin, LI Jing

(College of Mathematics and Information Science，Xinyang Normal University，Xinyang 464000，China)

The complete biharmonic submanifolds in a Riemannian manifolds with sectional curvature bounded from above by a non-negative constant are investigated by using integral by parts. If the integral of their mean curvature satisfies some growth conditions, then their mean curvature is a constant. In particular, the mean curvature of the complete biharmonic submanifolds is bounded as 1 in a sphere and satisfies some growth growth conditions, then the mean curvature is 1. So an affirmative partial answer to BMO conjecture and S.Meata′s Conjecture is obtained.

biharmonic maps, biharmonic submanifolds, biminimal submanifolds

2015-04-07

信阳师范学院青年基金(2014-QN-061)和信阳师范学院研究生科研创新基金(2014KYJJ29)。

冯书香，女，山东菏泽人，硕士，信阳师范学院数学与信息科学学院讲师，主要从事微分几何研究。

时间：2016-1-5 13:01 网络出版地址：http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.003.html

O186.12

A

1007-4260(2015)04-0012-03

10.13757/j.cnki.cn34-1150/n.2015.04.003