地电阻率三维影响系数及其应用
2015-07-01解滔卢军
解 滔 卢 军
(中国地震台网中心, 北京 100045)
地电阻率三维影响系数及其应用
解 滔 卢 军
(中国地震台网中心, 北京 100045)
采用有限元数值方法, 计算了对称四极装置观测时测区介质对地电阻率观测的三维影响系数分布。计算结果表明, 表层介质整体影响系数为正和为负时, 表层介质各区域影响系数的分布形态相近, 不同层状电性结构三维影响系数分布形态也相似。在地表二维平面, 影响系数在供电电极和测量电极之间存在近似椭圆的负区域, 其余区域影响系数为正。沿测线垂直剖面, 影响系数在供电电极和测量电极之间存在近似半椭圆的负区域, 其余区域影响系数为正。在三维空间上, 观测系统布设于地表时影响系数为负的区域位于供电电极和测量电极间的近似半椭球区域, 影响系数在靠近电极附近显著大于其余区域。在测区地表局部介质电阻率发生变化时, 可依据影响系数分布定性地分析其对地电阻率观测的影响, 为进一步实验和数值模型定量分析提供参考。
地电阻率 有限元 影响系数 层状介质 地震 异常
0 引言
中国于1966年河北邢台MS7.2地震后引入物探视电阻率方法应用于地震预测实验观测, 目前在主要活动断裂带和人口密集的大中城市附近地震活动区共有70余个地电阻率(中国地震局地电观测规范中将视电阻率称为地电阻率)台站担负着常规的地震监测任务。在近50a的连续监测中多次记录到了发生在台网内的中强地震(如1976年唐山MS7.8、 松潘-平武MS7.2, 1998年张北MS6.2, 2003年大姚MS6.2、 民乐-山丹MS6.1和2008年汶川MS8.0地震等)前突出的地电阻率异常(钱复业等, 1982, 1990; 桂燮泰等, 1989; 高立新等, 1999; Luetal., 1999; 叶青等, 2005; 张学民等, 2009; 杜学彬, 2010)。为分析地电阻率变化与测区介质电阻率变化之间的关系, 中国地电工作者发展了层状介质一维影响系数理论。地电阻率影响系数理论表明, 地电阻率的相对变化可以表述成测区不同区域介质电阻率相对变化的加权和(钱家栋等, 1985, 1998, 2013; Parketal., 1991; Luetal., 2004)。研究表明, 对于某些特定的电性结构, 浅层介质的一维影响系数为负, 并以此解释了中国某些台站观测到的夏高冬低型反常年变现象(Luetal., 2004)。钱家栋等(1988)提出了地电阻率多极距观测设想, 在层状介质模型假设下采用一维影响系数理论反演测区地下各层介质电阻率随时间的变化, 进而提取由孕震应力引起的深部介质电阻率异常。地电工作者于20世纪80年代在四川郫县台、 云南大理台和甘肃平凉台进行了地电阻率多极距实验观测, 并利用一维影响系数理论反演出各层介质随时间的变化以及深部介质电阻率在地震前的异常变化(赵和云等, 1987; 薛顺章等, 1994)。以上关于一维影响系数的工作假定测区地下介质为水平层状分布, 并且各层介质电阻率是整体变化的。在分析诸如降雨和地下水位变化引起某一厚度范围内介质电阻率整体性变化对地电阻率观测的影响时, 这种假设对实际情况有较好的近似。但是, 当并非各层介质电阻率整体发生变化, 而是各层内局部区域介质电阻率发生变化时, 采用一维影响系数理论将无法予以分析。近些年随着社会经济的发展, 许多地电阻率台站测区观测环境受到干扰和破坏, 引起地表局部介质电阻率发生变化。为分析局部介质电阻率变化对地电阻率观测的影响, 文章采用有限元数值分析方法计算了对称四极装置观测时测区介质的三维影响系数分布。
1 影响系数理论
中国定点地电阻率台站观测采用对称四极观测装置, 1个台站一般布设2条相互垂直的测道或2条相互垂直加1条斜测道共3个测道, 图1 为观测装置示意图。如果将地电阻率测区划分为任意的N块区域, 每一块区域介质电阻率为ρi,i=1, 2, …,N。在测区电性结构确定、 观测装置和极距以及布极位置确定时, 地电阻率ρa是各分区介质电阻率的函数(钱家栋等, 1985, 1998; Parketal., 1991; Luetal., 2004):
(1)
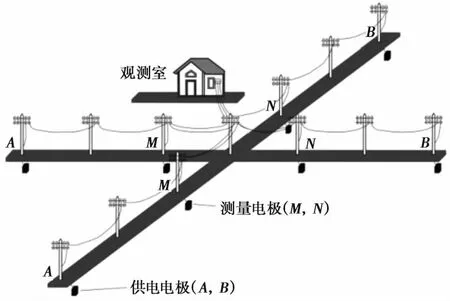
图1 对称四极观测装置示意图Fig. 1 Diagrammatic graph of Schlumberger arrays.
在多数情况下, 各分区介质电阻率在一定时间内的相对变化很小, Δρi/ρi≪1, 因此将式(1)进行Taylor级数展开, 二阶及高阶项远远小于一阶项, 可忽略不计。地电阻率的相对变化可以简单地表示为各分区介质电阻率相对变化的加权和:
(2)
式(2)中Bi被称为影响系数:
(3)
影响系数Bi满足如下关系(Seigel, 1959; Royetal., 1981; Wait, 1981):
(4)
若按照N层水平层状结构将测区划分为N块区域, 则可采用电位分布解析表达式和地电阻率滤波器算法计算对称四极装置相应的一维影响系数(O’Neilletal., 1984; 姚文斌, 1989)。若将测区介质按任意大小三维体划分, 则可采用数值计算方法计算各区域介质对地电阻率观测的三维影响系数。
2 分析方法
采用对称四极装置进行观测时, 地电阻率观测值是测区地下一定体积内介质电阻率的综合表征, 距离更远和深度更深的介质对观测的影响可以忽略。目前中国地电阻率观测供电极距多为AB=1000m, 地电阻率观测实践也表明, 地表局部电性结构变化区域在测线附近时才能对观测产生显著的影响, 因此文中对布极中心点周围2000m×2000m×1000m范围内介质的三维影响系数采用有限元数值分析方法予以分析。
2.1 稳恒电流场有限元方法
地电阻率定点台站观测采用对称四极装置, 观测时在供电电极A、B输入直流电流, 在测量电极M、N测量电势差, 此问题可视为稳恒电流场计算, 电流场遵守Maxwell方程组和电荷守恒定律, 电位分布满足Possion方程:

(5)
式(5)中,V是由电流源I产生的电位,σ是介质电导率,δ(x,y,z)是Dirac delta函数。
有限介质空间的全部边界为Γ, 一部分边界没有电流流出(如地表), 满足Neumann边界条件, 记为Γs, 其余边界记为Γv, 满足Dirichlet边界条件, 因此方程(5)满足边界条件
(6)

应用虚功原理可得到稳恒电流场Possion方程的有限元弱解形式:
(7)
式(7)中,Ω为计算区域,φ为任意的虚位移函数, 在满足Dirichlet边界条件的边界上, 虚位移函数φ=0。
由于电位V在电流源处存在奇异性, 数值求解式(7)时在电流源附近得到的结果误差较大。常用的去除奇异性的方法是将电流源产生的电位分解为由供电电流在均匀半空间介质(σp)中产生的一次场电位Vp和非均匀介质(σs)引起的2次场电位Vs, 且满足V=Vp+Vs和σs=σ-σp。一次场电位Vp可以通过解析表达式得到, 2次场电位Vs通过单元离散化后数值计算得到(Lowryetal., 1989; Zhaoetal., 1996)。
地电阻率观测在地表自然地满足Neumann边界条件, 在水平方向和垂直方向(深度)可视为无穷远边界, 可以施加Dirichlet边界条件(V=0), 也可以施加Neumann边界条件(Coggon, 1971)。但是, 建立的模型在水平和垂直方向上的尺度不可能是无限的, 对于一固定尺寸的模型, 在供电极距AB大于一定的值后, 对无穷远边界施加Dirichlet边界条件时计算得到的地电阻率值将小于实际值, 而对无穷远边界施加Neumann边界条件时计算得到的地电阻率值将大于实际值(Deyetal., 1979; Lietal., 2005)。对固定的供电极距AB, 模型尺寸越大, 边界对计算结果的影响就越小; 但是模型越大, 计算量也就越大, 因此需要合理地选择模型水平方向的尺寸和最底层厚度。解滔等(2014)在对四平台地电阻率观测有限元数值分析中认为, 模型水平尺寸>6倍AB、 模型厚度 >2倍AB时, 边界效应对计算的影响已低于仪器的观测精度。模型经单元离散化、 施加电流源和边界条件后可对单元节点上的自由度(电位)进行数值求解, 求解出电位分布后可以获得测量电极间的电位差, 进而依据对称四极装置系数计算地电阻率和相应的影响系数分布。
2.2 模型建立


图2 H型电性结构和一维影响系数Fig. 2 H type electric structure and its one-dimensional sensitivity coefficients.

图3 K型电性结构和一维影响系数Fig. 3 K type electric structure and its one dimensional sensitivity coefficients. 虚线部分表示影响系数为负

图4 模型示意图Fig. 4 Diagrammatic graph of model.
模型中供电极距AB=1000m, 测量极距MN=300m, 观测装置位于模型表面, 模型水平尺寸取7倍AB, 按图2a和图3a电性结构将模型划分为3层, 最底层厚度取2倍AB, 影响系数计算区域为布极中心点周围2000m×2000m×1000m的空间范围, 图4 为模型示意图。由式(3)可知, 在电性结构一定时, 某一分块区域影响系数不受其余区域分块大小的影响, 因此模型中将分析区域均匀划分为4m×4m×4m的立方体单元, 其余区域单元划分由内到外逐渐扩大, 以节省计算空间和时间。计算时在电极A输入2I电流, 在电极B处输入-2I电流, 对分析区域内每个单元采用中心差分逐一计算式(3)中的偏微分部分, 进而计算其影响系数。
3 三维影响系数分布

图5 图2a中H型电性结构的三维影响系数分布Fig. 5 Three-dimensional sensitivity coefficients distribution of H type electric structure in Fig 2a.
图2a中H型电性结构的三维影响系数在地表和沿测线剖面的分布示于图5。从图5a可以看出, 地表二维平面对称四极装置地电阻率观测影响系数在测量极和供电极之间存在2个近似椭圆的负区域, 其余区域为正。影响系数(绝对值)在靠近电极时大于其余区域, 同时影响系数呈现出关于测线和过布极中心垂直于测线方向的对称性。在2个影响系数为负的椭圆区域内, 介质电阻率的降低将会引起地电阻率观测值的升高, 反之亦然。在沿测线的垂直剖面上影响系数在供电极和测量极之间呈现出与地表分布对应的负区域(图5b), 其余区域影响系数为正。在三维空间上, 地表地电阻率观测影响系数在测量极和供电极之间存在近似半椭球的负区域, 其余区域为正。图3a中K型电性结构三维影响系数在地表和测线剖面的分布见图6, 同样地在测量极和供电极之间存在影响系数为负的近似半椭球区域。对比2种电性结构三维影响系数的分布可以发现, 尽管二者影响系数为负的区域大小有些差别, 但二者总体分布特征是一致的。
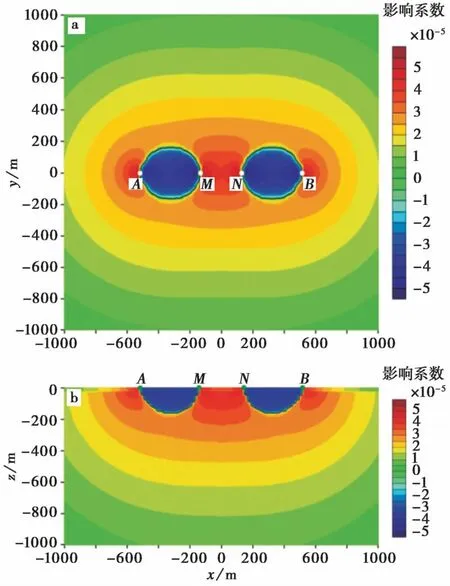
图6 图3a中K型电性结构的三维影响系数分布Fig. 6 Three-dimensional sensitivity coefficients distribution of K type electric structure in Fig 3a.
4 应用实例
地电阻率三维影响系数分布揭示了各区域介质电阻率变化对地电阻率观测值的影响程度, 为分析地电阻率观测值变化和测区局部介质电阻率变化之间的关系提供了依据。近些年随着社会经济的发展, 许多台站测区地表观测环境受到不同程度的破坏和干扰, 并引起观测值相应的变化, 给异常分析和震情判定带来了困难。在异常核实工作中可将这些干扰源视为局部介质电阻率发生了变化, 依据三维影响系数在地表的分布迅速定性地判断干扰源对观测的影响形态, 并可以结合不同测道的观测值排除或锁定某些干扰源, 为下一步的实验或模型数值分析提供参考。文中以甘肃临夏台的干扰排除和云南腾冲台地电阻率异常认定及震情判定为例, 说明三维影响系数在异常核实和异常分析中的应用。
4.1 临夏台干扰排除
临夏地电阻率台站位于临夏市东北约7km的折桥乡, 大地构造上位于鄂尔多斯地块、 阿拉善地块和青藏地块的交接部位, 次级构造上位于祁连山和甘东南次级地块交接部位(严玲琴等, 2013)。地电阻率观测布设了SN和EW 2道测线, 2测道供电极AB=1500m,MN=500m, 布极方式与各电极分布情况如图7a所示。临夏台SN测道地电阻率观测值从2007年出现年变畸变, 经核实与SN测道南供电极和南测量电极之间同期修建民房有关。该测道自2009年年初开始出现破年变加速下降变化, 下降幅度约5.9%, 扣除正常年变化幅度后下降幅度约2.3%, 并于2010年下半年开始回返。EW测道观测值从2009年年初也出现破年变加速下降变化, 下降幅度约5.1%, 扣除正常年变化幅度后下降幅度约1.6%, 并于2010年下半年回返(图7b)。电磁学科工作组于2011年7月前往临夏台对2测道自2009年出现的同步变化开展异常现场核实工作。经现场勘察和与台站工作人员及周围居民咨询了解到, 自2008年年底开始SN测道南供电极和南测量电极之间开始动工修建粮油市场和仓库, 随后施工规模扩大。在EW测道西供电极和西测量电极之间挖土供砖厂烧制, 土坑深约2m, 宽约80m, 长约150m, 2010年挖土区域扩展至西供电极约2m处(图7a)。粮油市场和仓库在地表挖土后建设了混凝土地下室, 与原有土层介质相比, 该区域介质电阻率升高。砖厂土坑开挖的区域可视为无穷大的空气介质, 与之前土层介质相比该区域电阻率升高。从地电阻率对称四极观测装置测区介质三维影响系数在地表的分布来看, 2测道受干扰的区域均位于影响系数为负的区域, 该区域介质电阻率的升高将引起地电阻率观测值的降低, 因此工作组认为粮油市场、 仓库建设和砖厂土坑开挖引起的干扰变化与观测值变化在形态上是一致的。但观测值的下降幅度是否完全或大部分是由干扰源引起的, 还需要进一步的分析。为此工作组于第2日对EW测道西供电极附近砖厂土坑开挖开展了实验分析, 结果认为土坑开挖能引起EW测道观测值约1.1%的下降变化*杜学彬, 2011, 关于临夏台土坑干扰实验的解释。, 为此认为EW测道2009年开始的下降变化主要是由土坑开挖引起的干扰变化。SN测道附近的粮油市场和仓库的规模大于EW测道的土坑, 其受干扰下降的幅度也应大于1.1%, 因此也认为SN测道2009年开始的下降变化主要是由干扰引起的。在观测资料恢复正常变化后该区域未有强地震发生, 也说明临夏台2测道的此次变化不是地震前兆异常。
4.2 腾冲台异常认定

图7 临夏台布极图和2006—2011年观测曲线Fig. 7 Diagrammatic graph of Linxia station and observed data from 2006 to 2011.
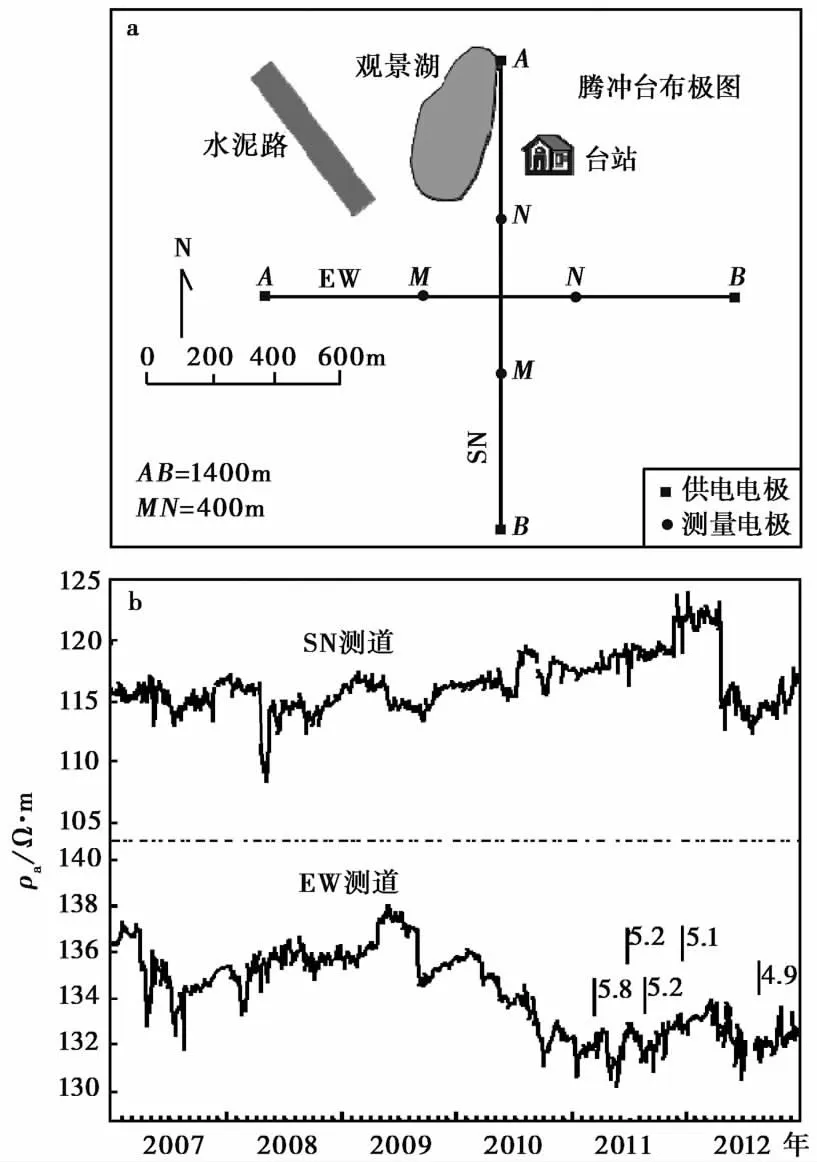
图8 腾冲台布极图和2007—2012年观测曲线Fig. 8 Diagrammatic graph of Tengchong station and observed data from 2007 to 2012.
腾冲盆地位于大盈江断裂向SE凸的弧顶部位, 腾冲台位于盆地东南缘后山断层与上马厂断层交会的东侧后山断层的SE盘上。腾冲旧台布设有EW和SN 2个测道, 2测道供电极AB=1400m,MN=400m, 布极方式与各电极分布情况如图8a所示。2012年底由于受到县城扩建的干扰, 地电阻率观测场地搬迁至旧台址东南1500m处, 新台采用长短极距2套观测系统。腾冲台地电阻率EW测道在2010年4月开始出现加速下降, SN测道同期出现上升变化, 截至2011年5月, EW测道累计下降幅度约3.7%, SN测道累计上升幅度约2.6%(图8b)。腾冲台测区为农业用田, 冬季地下水位<1m, 夏季为水覆盖, 因而腾冲台地电阻率年变化幅度很小。异常出现后电磁学科组与台站工作人员咨询测区观测环境变化情况, 从2010年4月份以来, 地电阻率测区西北边农田被开发建设水泥路和观景湖(图8a)。新建水泥路可视为高阻体; 观景湖为土层开挖蓄水, 可视为低阻体。从地电阻率对称四极观测装置测区介质三维影响系数在地表的分布来看, 水泥路位于SN测道影响系数为正的区域, 主体部分也位于EW测道影响系数为正的区域; 观景湖位于SN测道影响系数为负的区域, 但位于EW测道影响系数为正的区域。水泥路与2测道的位置相近, 将引起2测道观测值上升。观景湖将引起SN测道观测值的上升变化, 而引起EW测道观测值的下降变化, 与2测道观测值的变化形态一致。从水泥路和观景湖的规模和相对测线的位置来看, 观景湖产生的影响是主要的。观景湖更为靠近SN测道, 对SN测道的影响幅度应显著大于对EW测道的干扰幅度, 但是EW测道观测值下降幅度却大于SN测道的上升幅度, 同时水泥路会引起EW测道观测值的上升变化。观景湖和水泥路不能解释EW测道出现的下降变化, 因此认为至少在EW测道的下降变化中包含有前兆信息。随后于2011年3月10日发生了盈江MS5.8地震(震中距65km)、 2011年6月20日腾冲MS5.2地震(震中距20km)、 2011年8月9日腾冲MS5.2地震(震中距21km)、 2011年11月28日中缅交界MS5.1地震(震中距92km), 在2012年EW测道观测值再次出现下降变化后于2012年9月11日发生施甸MS4.9地震(震中距76km)。
5 讨论和结论
5.1 讨论
一维层状介质影响系数将每一层介质视为整体性变化, 从而分析每一层介质电阻率变化对地电阻率观测的影响。季节性降雨、 浅层介质温度变化以及地下水位变动近似认为可引起某一厚度范围内介质电阻率的整体性变化。由于地电阻率是探测测区地下一定体积内介质的电阻率变化, 在应力作用下测区深部介质电阻率也可视为整体性变化(不考虑电阻率各项异性变化), 因而可以采用一维影响系数分析这些因素对地电阻率的影响, 比如地电阻率年变化和趋势性变化。三维影响系数更为精细地反映了各区域介质对地电阻率观测的影响, 总体而言, 测线附近的介质对观测影响较大, 电极附近最为显著, 随着各区域与测线的距离增加, 影响系数降低, 超过一定距离后可认为其对观测没有影响。
对每一层介质, 该层各区域三维影响系数之和与该层的一维影响系数相等, 因而在分析层状介质电阻率整体性变化时二者是等价的。当测区局部介质电阻率发生变化时, 一维影响系数不再适用, 而采用三维影响系数则可以进行分析。已有观测经验指出, 在地表供电极和测量极之间的介质电阻率变化将引起地电阻率观测值相反的变化, 其余区域则引起观测值相同的变化, 与文中计算的三维影响系数分布大体一致。但是三维影响系数分布表明, 影响系数为负的区域位于供电极和测量极之间近似半椭球的区域(地表为似椭圆), 并非供电极和测量极之间的所有区域。图3b中K型电性结构表层介质一维影响系数在AB=1000m时为负, 表层负区域影响系数之和的绝对值要大于表层其余区域影响系数之和, 因而对于这类电性结构, 在负区域若出现干扰源, 对观测的影响较大。
目前多数地电阻率台站受到不同程度的干扰和破坏, 这些干扰源可能引起一些虚假异常现象, 或者产生的干扰与孕震信息耦合在一起, 进而影响地电阻率前兆异常分析。在对台站进行异常核实工作时, 可依据三维影响系数分布迅速判定干扰源对地电阻率观测可能产生的影响形态, 为进一步定量分析提供参考。同时对某些干扰源, 可结合不同测道观测值的变化形态、 幅度和三维影响系数分布直接予以排除或者认定异常。
5.2 结论
文中采用有限元数值分析方法对对称四极装置地电阻率地表观测测区介质三维影响系数进行了计算, 得到了一些有意义的结果:
(1)影响系数在供电极和测量极之间存在近似半椭球的负区域, 其余区域影响系数为正; 影响系数在测线附近较大, 靠近电极处更为显著, 远离测线区域介质影响系数迅速降低。
(2)地表影响系数较大, 说明在地表进行地电阻率观测时易受地表干扰源的影响。深部介质影响系数为正, 在深部介质电阻率受应力作用发生变化时, 地电阻率观测将得到一致的变化形态。
(3)依据三维影响系数分布可以迅速判定测区地表局部介质电阻率变化对观测的影响形态, 为进一步分析提供参考。同时结合地电阻率各测道观测值, 可以直接对某些干扰源予以排除, 进而进行前兆异常分析。
致谢 审稿专家对本文提出了中肯的修改建议, 在此表示衷心的感谢!
杜学彬. 2010. 地震预报中的2类视电阻率变化 [J]. 中国科学(D辑), 40(10): 1321—1330.
DU Xue-bin. 2010. Two types of changes in apparent resistivity in earthquake prediction [J]. Science in China(Ser D), 40(10): 1321—1330(in Chinese).
高立新, 黄根喜, 阎海滨. 1999. 张北-尚义6.2级地震(1998-01-10)前倾斜与地电阻率前兆异常 [J]. 地壳形变与地震, 19(4): 88—90.
GAO Li-xin, HUANG Gen-xi, YAN Hai-bin. 1999. Anamolies of crustal inclination and geoelectric resistivity before Zhangbei-ShangyiMS6.2 earthquake [J]. Crustal Deformation and Earthquake, 19(4): 88—90(in Chinese).
桂燮泰, 关华平, 戴经安. 1989. 唐山、 松潘地震前视电阻率短临异常图像重现性 [J]. 西北地震学报, 11(4): 71—75.
GUI Xie-tai, GUAN Hua-ping, DAI Jing-an. 1989. The short-term and immediate anomalous pattern recurrences of the apparent resistivity before the Tangshan and Songpan earthquake of 1976 [J]. Northwestern Seismological Journal, 11(4): 71—75(in Chinese).
钱复业, 赵玉林, 刘婕, 等. 1990. 唐山7. 8级地震地电阻率临震功率谱异常 [J]. 地震, 10(3): 33—38.
QIAN Fu-ye, ZHAO Yu-lin, LIU Jie,etal. 1990. Power spectrum anomaly of earth resistivity immediately before TangshanMS7.8 earthquake [J]. Earthquake, 10(3): 33—38(in Chinese).
钱复业, 赵玉林, 于谋明, 等. 1982. 地震前地电阻率异常变化 [J]. 中国科学(B辑), (9): 831—839.
QIAN Fu-ye, ZHAO Yu-lin, YU Mou-ming,etal. 1982. Geo-resistivity anomaly before earthquake [J]. Science in China(Ser B), (9): 831—839(in Chinese).
钱家栋, 曹爱民. 1998. 1976年唐山7.8级地震地电阻率和地下水前兆综合物理机制研究 [J]. 地震, 18(增刊): 1—9.
QIAN Jia-dong, CAO Ai-min. 1998. Research on comprehensive mechanism of precursors in apparant resistivity and water table associated with 1976 Tangshan earthquake(M=7.8)[J]. Earthquake, 18(Suppl): 1—9(in Chinese).
钱家栋, 陈有发, 金安忠. 1985. 地电阻率法在地震预报中的应用 [M]. 北京: 地震出版社.
QIAN Jia-dong, CHEN You-fa, JIN An-zhong. 1985. The Geo-resistivity Method Used in Earthquake Prediction [M]. Seismological Press, Beijing(in Chinese).
钱家栋, 马钦忠, 李劭秾. 2013. 汶川MS8.0地震前成都台NE测线地电阻率异常的进一步研究 [J]. 地震学报, 35(1): 4—17.
QIAN Jia-dong, MA Qin-zhong, LI Shao-nong. 2013. Further study on the anomalies in apparent resistivity in the NE configuration at Chengdu station associated with WenchuanMS8. 0 earthquake [J]. Acta Seismo Sinica, 35(1): 4—17(in Chinese).
钱家栋, 赵和云. 1988. 地电阻率的数值模拟和多极距观测系统 [J]. 地震学报, 10(1): 77—89.
QIAN Jia-dong, ZHAO He-yun. 1988. Earth resistivity modeling and observational system with multi-separation of electrodes [J]. Acta Seismo Sinica, 10(1): 77—89(in Chinese).
解滔, 王洪岐, 刘立波, 等. 2014. 四平台地电阻率相反年变有限元数值分析 [J]. 地球物理学进展, 29(2): 588—594.
XIE Tao, WANG Hong-qi, LIU Li-bo,etal. 2014. Inverse annual variations of apparent resistivity at Siping earthquake station by using finite method [J]. Progress in Geophysics, 29(2): 588—594(in Chinese).
薛顺章, 温新民, 董永德, 等. 1994. 地电阻率预报地震新方法的研究 [J]. 地震学报, 16(2): 227—234.
XUE Shun-zhang, WEN Xin-min, DONG Yong-de,etal. 1994. Analysis on new earthquake prediction method using apparent resistivity [J]. Acta Seismo Sinica, 16(2): 227—234(in Chinese).
严玲琴, 郑卫平, 张辉, 等. 2013. 临夏台地电阻率变化与震兆现象分析 [J]. 中国地震, 29(1): 168—176.
YAN Ling-qin, ZHENG Wei-ping, ZHANG Hui,etal. 2013. Analysis on the variation of the earth resistivity and seismic precursory phenomena at Linxia seismic station, Gansu [J]. Earthquake Research in China, 29(1): 168—176(in Chinese).
姚文斌. 1989. 电测深数值计算和解释入门 [M]. 北京: 地震出版社.
YAO Wen-bin. 1989. Introduction of Electrical Sounding Numerical Computation and Explanation [M]. Seismological Press, Beijing(in Chinese).
叶青, 杜学彬, 陈军营, 等. 2005. 2003年大姚和民乐-山丹地震1年尺度预测 [J]. 地震研究, 28(3): 226—230.
YE Qin, DU Xue-bin, CHEN Jun-ying,etal. 2005. One-year prediction for the Dayao and Minle-Shandan earthquakes in 2003 [J]. Journal of Seismological Research, 28(3): 226—230(in Chinese).
张学民, 李美, 关华平. 2009. 汶川8.0 级地震前的地电阻率异常分析 [J]. 地震, 29(1): 108—115.
ZHANG Xue-min, LI Mei, GUAN Hua-ping. 2009. Anomaly analysis of earth resistivity observations before the Wenchuan earthquake [J]. Earthquake, 29(1): 108—115(in Chinese).
赵和云, 钱家栋. 1987. 郫县台多极距观测资料的反演和分析 [J]. 中国地震, 3(增刊): 73—78.
ZHAO He-yun, QIAN Jia-dong. 1987. Inversion and analysis of data of temporal changes in apparent resistivity with multi-separations in Pixian stations, Sichuan Province [J]. Earthquake Research in China, 3(Suppl): 73—78(in Chinese).
Coggon J H. 1971. Electromagnetic and electrical modeling by the finite element method [J]. Geophysics, 36: 132—155.
Dey A, Morrison H F. 1979. Resistivity modeling for arbitrary shaped three-dimensional structures [J]. Geophysics, 44(4): 753—780.
Li Y G, Spitzer K. 2005. Finite element resistivity modeling for three-dimensional structures with arbitrary anisotropy [J]. PEPI, 150: 15—27.
Lowry T, Allen M B, Shive P N. 1989. Singularity removal: A refinement of resistivity modeling techniques [J]. Geophysics, 54: 766—774.
Lu J, Qian F Y, Zhao Y L. 1999. Sensitivity analysis of the Schlumberger monitoring array: Application to changes of resistivity prior to the 1976 earthquake in Tangshan, China [J]. Tectonophysics, 307(3-4): 397— 405.
Lu J, Xue S Z, Qian F Y,etal. 2004. Unexpected changes in resistivity monitoring for earthquakes of the Longmen Shan in Sichuan, China, with a fixed Schlumberger sounding array [J]. PEPI, 145(1-4): 87—97.
O’Neill D J, Merrick N P. 1984. A digital linear filter for resistivity sounding with a generalized electrode array [J]. Geophys Prospect, 32(1): 105—123.
Park S K, Van G P. 1991. Inversion of pole-pole data for 3-D resistivity structure beneath arrays of electrodes [J]. Geophysics, 56(7): 951—960.
Roy A, Poddar M. 1981. A simple derivation of Seigel’s time domain induced polarization formula [J]. Geophys Prospect, 29(1): 432— 437.
Seigel H O. 1959. Mathematical formulation and type curves for induced polarization [J]. Geophysics, 24(3): 547—565.
Wait J R. 1981. Towards a general theory of induced electrical polarization in geophysical exploration [J]. IEEE Trans Geosci Remote Sensing GE, 19(4): 231—234.
Zhao S, Yedlin M. 1996. Some refinement on the finite-difference method for 3-D dc resistivity modeling [J]. Geophysics, 61: 1301—1307.
THREE-DIMENSIONAL SENSITIVITY COEFFICIENTS OF APPARENT RESISTIVITY AND PRELIMINARY APPLICATION
XIE Tao LU Jun
(ChinaEarthquakeNetworksCenter,Beijing100045,China)
We calculate three-dimensional sensitivity coefficients distribution of apparent resistivity observation when Schlumberger array is used by using finite element method. Analysis results suggest that for the situation of one-dimensional positive or minus coefficient of surface medium, three-dimensional sensitivity coefficients distribution at surface shows similar patterns, and sensitivity coefficients distributions of different layered electric structures are also similar. There are two approximate ellipses at the two-dimensional surface plane between current electrodes and potential electrodes, where sensitivity coefficients are minus, and sensitivity coefficients at other areas are positive. Sensitivity coefficients at two approximate ellipses between current electrodes and potential electrodes are minus at the vertical section along monitoring line, while others are positive. From the three-dimensional view, minus sensitivity coefficients are at the two approximate half ellipsoids between current electrodes and potential electrodes when arrays are applied at surface. And coefficients near the electrodes are much greater than other areas. When resistivity of local areas at surface changes, we can qualitatively analyze the disturbing effects caused by the areas using three dimensional sensitivity coefficients distribution, and the analysis result can serve as reference for further experiment and numerical model quantitative analysis.
apparent resistivity, finite element, sensitivity coefficient, layered model, earthquake, anomaly
10.3969/j.issn.0253- 4967.2015.04.015
2014-08-06收稿, 2015-10-20改回。
国家自然科学基金(41374080)和中国地震局监测预报司震情跟踪定向工作任务(2014020402)共同资助。
P631.3+22
A
0253-4967(2015)04-1125-11
解滔, 男, 1986年生, 2011年于中国地震局兰州地震研究所获固体地球物理学专业硕士学位, 助理研究员, 主要从事地震电磁学及卫星热红外遥感应用研究, 电话: 010-59959144, E-mail: xtaolake@163.com。
