大甸子井-含水层系统水文地质参数间的变化关系

丁风和 戴 勇* 宋慧英 魏建民 查 斯

1)内蒙古自治区地震局， 呼和浩特 010010 2)内蒙古大学交通学院， 呼和浩特 010020

大甸子井-含水层系统水文地质参数间的变化关系

丁风和1)戴 勇1)*宋慧英2)魏建民1)查 斯1)

1)内蒙古自治区地震局， 呼和浩特 010010 2)内蒙古大学交通学院， 呼和浩特 010020

基于弹性力学和流体力学等相关理论， 利用气压系数和潮汐因子， 研究了大甸子井-含水层系统在不排水状态下的水文地质参数。结果表明， 孔隙度与固体骨架的体积压缩系数、 含水层内水的体积压缩系数、 贮水率、 渗透系数和导水系数间呈明显的幂函数关系。固体骨架的体积压缩系数、 贮水率、 渗透系数和导水系数随着孔隙度的增大而增大， 含水层内水的体积压缩系数随着孔隙度的增大而减小。固体骨架和含水层内水的体积压缩系数满足一元二次多项式关系， 且含水层内水的体积压缩系数要比固体骨架的体积压缩系数大， 水更易压缩。另外， 随着贮水率的增大， 渗透系数和导水系数也呈线性增大。

大甸子井 承压井-含水层系统 水文地质参数 不排水状态

0 引言

水文地质参数是表征含水介质水文地质性能的重要数量指标， 具有明确的物理基础与机理。一般情况下， 水文地质工作者确定水文地质参数的途径主要通过水文地质试验法(譬如抽、 注水实验， 渗水试验和达西试验等)和地下水动态观测资料(配线法和局部均衡法等)来确定(李义昌， 1995)， 但这些实验和方法需要花费较大的人力、 物力和财力。而对于地震工作者来说， 利用井潮、 气压等资料来分析井-含水层系统的固体潮效应、 气压效应、 以及它们与含水层水文地质参数(孔隙度， 介质的体积压缩系数， 贮水率和导水系数等)的关系等方面的研究较多(Bredehoeft， 1967； Kampetal.， 1983； Narasinmhanetal.， 1984； 田竹君等， 1985； Rojstaczer， 1988； 张昭栋等， 1989， 1995； 李春洪等， 1990； 骆鸣津等， 1990； Johnetal.， 1991； Erskine， 1991； 王礼恒等， 2012； Guietal.， 2013)。例如， 在不排水状态下， 给出气压系数或是潮汐因子和孔隙度、 固体骨架的体积压缩系数、 水的体积压缩系数间的定量关系。另外， 贮水率也与含水层介质的孔隙度和体积压缩系数存在定量关系， 在此基础上， 结合含水层厚度、 导压系数和潮汐波频率等， 井孔含水层的渗透系数和导水系数便可获得。

前人虽然在这些方面取得了非常重要的成果。但井-含水层系统的水文地质参数间存在怎样的变化规律， 其关系式是什么， 此类研究尚开展较少。本文以大甸子井数字化水位、 气压等资料为基础， 基于弹性力学、 岩石力学和流体力学的相关理论， 利用气压系数和潮汐因子等， 滑动拟合得到了不排水状态下大甸子井-含水层系统的孔隙度与固体骨架的体积压缩系数和含水层内水的体积压缩系数。相应的贮水率也可定量获得。另外， 结合含水层厚度、 导压系数、 井管半径和潮汐波频率等， 井孔含水层的渗透系数和导水系数便可获得， 并给出了它们的变化关系式。

1 观测井基本情况

大甸子井位于赤峰市敖汉旗大甸子乡， 是1口静水位观测井， 井况良好。多年来数据的连续性和稳定性很好， 产出的资料质量高。在区域多次中强地震前都有非常明显的异常反应， 该井水位变化的主要影响因素为气压、 降雨和固体潮(丁风和等， 2007)。大甸子井是开展潮汐因子和气压系数变化特征研究的理想观测井。该井自1993年正式观测， 井深200.76m。含水层岩性为石炭系砂岩、 砂板岩等， 且破碎强烈， 性脆。水位观测段为57.0～116.0m。水位埋深18.8m左右。各层岩性组成及相关信息见图1。

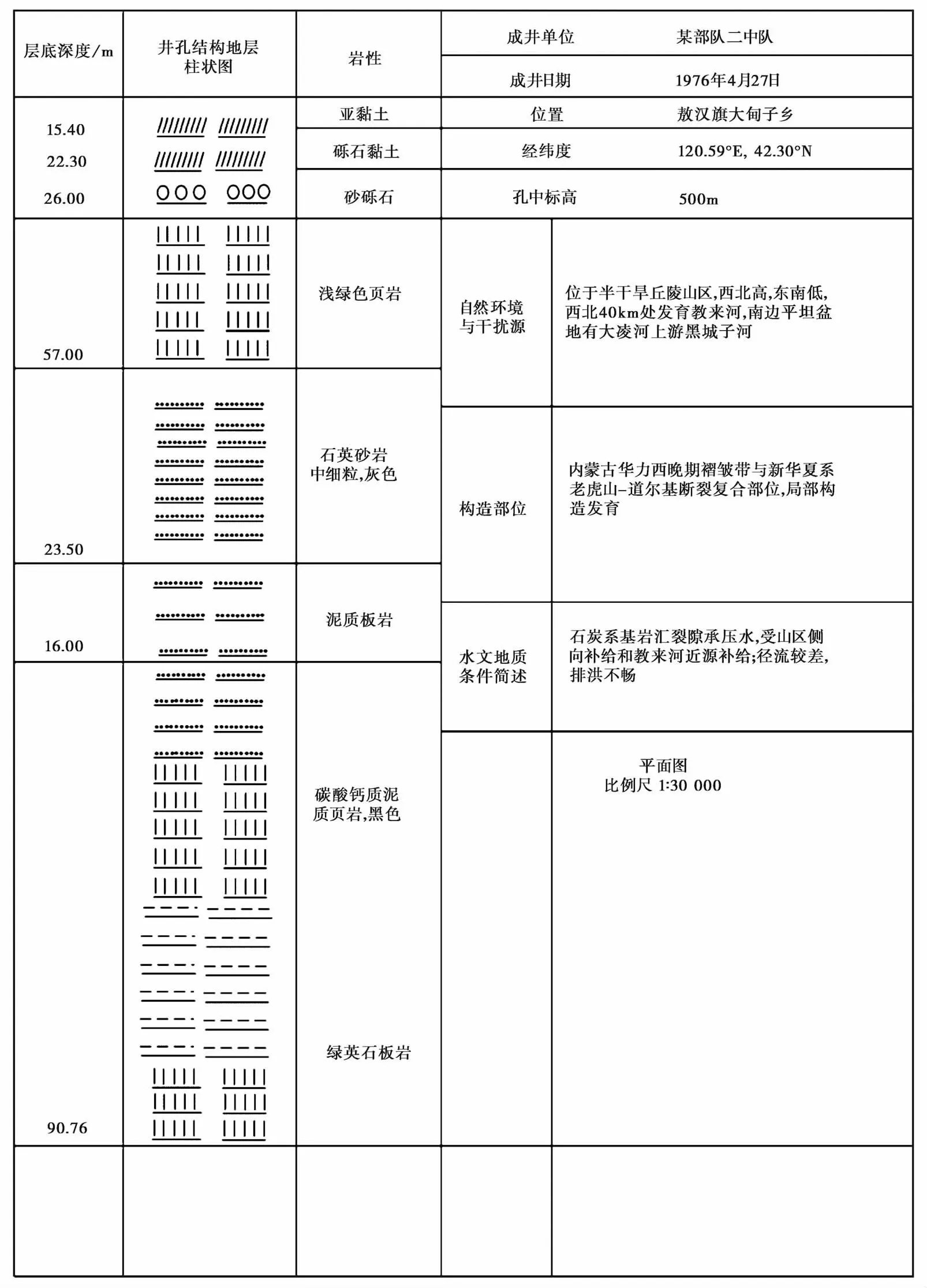
图1 大甸子井井孔剖面等基本情况Fig. 1 The basic situation of the borehole profile in Dadianzi Well.

2 含水层水文地质参数求取方法

依据前人的研究结果(Bredehoeft， 1967； 张昭栋等， 1989， 1995； 李春洪等， 1990)， 不排水状态下， 井水位的气压系数BP和潮汐因子Bg可分别表示为

(1)

(2)

式(1)、(2)联合可得到式(3)：

(3)

式(1)—(3)中，α为固体骨架的体积压缩系数，β为水的体积压缩系数，n为含水层的孔隙度，ρg为水的重度， 且ρg=0.098hPa/mm。

1)对潮汐因子Bg的获取来说， 由于维尼迪柯夫潮汐调和分析法， 可同时消除观测数据中的基线差、 时间一次项的线性变化与时间二次项的非线性变化， 在很大程度上可削弱和降低降水、 气温和气压等非体应变参数对井水位潮汐观测的影响(刘序俨等， 2009)。同时， 考虑到处于中纬度地区的大甸子井水位M2波振幅最大， 它具有最大的信噪比。因此， 可直接利用该井原始水位进行M2波潮汐调和分析来获取潮汐因子等参数。2)气压系数BP可由高阶差分(张昭栋， 1986； 殷积涛等， 1988)得到， 本文研究取0—3阶差分中水位和气压相关系数最大的那阶， 用一元线性回归滑动求得。3)含水层的孔隙度n、 水的体压缩系数β依据式(3)亦可滑动得到。最后， 利用式(1)或式(2)即可求出固体骨架的体积压缩系数α。

相应的贮水率Ss也可按照式(4)求出(Davisetal.， 1966)：

(4)

动态响应条件下， 含水层的导水系数T、 渗透系数K、 潮汐波频率ω、 导压系数a和相位滞后φ等满足式(5)—(8)(李春洪等， 1990)：

(5)

(6)

(7)

T=KM

(8)

因为不排水状态下， 相位滞后的正切值为零， 开尔文函数的实部为零。因此， 含水层导压系数a可写为

(9)

(10)

接着渗透系数K和导水系数T可分别写为

(11)

(12)

式(5)—(12)中，φ为M2波相位滞后，k0为开尔文函数实部，r0为井径，T为含水层导水系数，ω为潮汐波中某一波群的固定频率(选择振幅大、 干扰少的M2波频率，ω=1.9324)，a为含水层导压系数，K为渗透系数，M为含水层厚度，T为导水系数。

最终可依据式(3)—(12)得到该井不排水状态下的相关含水层水文地质参数。

3 含水层水文地质参数间的变化关系

3.1 孔隙度和体积压缩系数的关系

从大甸子井含水层孔隙度和固体骨架体积压缩系数的关系可以看出(图2， 表1)， 二者间存在明显的幂函数性质， 即α=-b(1-n)c(c<0)。在第4象限内， 含水层介质固体骨架的体积压缩系数随着孔隙度的增大而增大(α为负仅表示取膨胀为负)。这归因于， 当骨架应力减小时， 骨架体积增大(膨胀)， 其体积变化量(或变化率)亦越大(易压缩)。因此， 骨架体积压缩系数随着孔隙度的增大而增大。

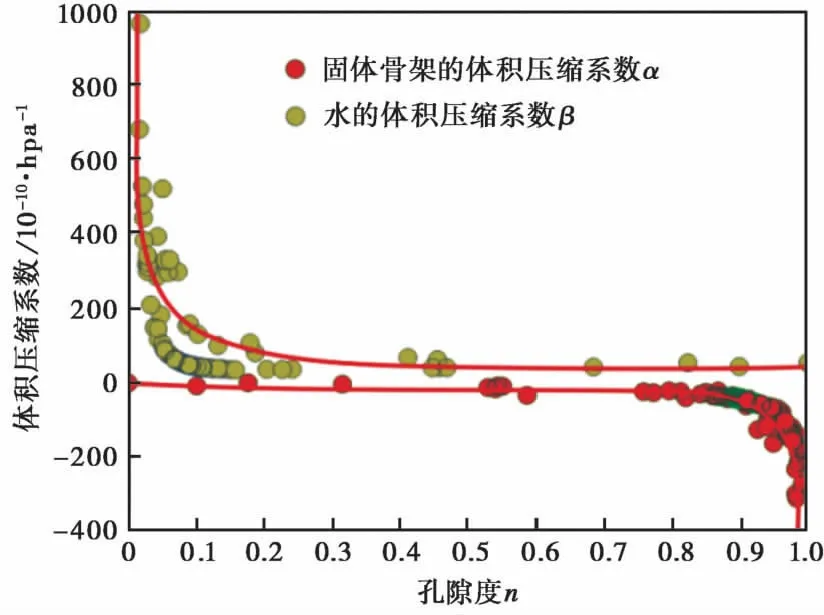
图2 大甸子井含水层孔隙度和体积压缩系数间的关系Fig. 2 The relationship between porosity and volume compression coefficient of aquifer for Dadianzi well.α为负、 β为正， 表示随孔隙度的增大， 取膨胀为负、 压缩为正

表1 大甸子井-含水层系统水文地质参数拟合结果

Table 1 Hydrogeologic parameter fitting results of Dadianzi well-aquifer system

序号参数拟合方程R2标准差1n与αα=-16.57(1-n)-0.53230.70130.972n与ββ=9.71n-1.1050.8113273.33α与ββ=0.025a2+0.25a-11.260.8799151.74n与SsSs=1.31(1-n)-0.55340.69252.8175n与KK=25.10(1-n)-0.68560.6232108.16n与TT=89.40(1-n)-0.55310.693192.27Ss与KK=34660Ss1.02.24e-128Ss与TT=6.8e+9Ss1.02.95e-5

注 在95%置信水平下， 各参数间相关系数的平方都>0.623 2， 方程拟合效果良好。

另外， 该井含水层孔隙度和水的体积压缩系数间， 亦存在明显的幂函数关系， 即β=bnc(c<0)。在第1象限， 含水层介质水的体积压缩系数随着孔隙度的增大而减小(β为正表示取压缩为正； 图2， 表1)。这是因为， 当孔隙压力增大时， 水体难压缩， 则水的体积压缩系数亦减小。

3.2 体积压缩系数间的关系

从该井含水层固体骨架和水的体积压缩系数间的拟合情况来看， 固体骨架和水的体积压缩系数之间满足一元二次多项式关系， 且水的体积压缩系数要比固体骨架的体积压缩系数大(图3， 表1)。

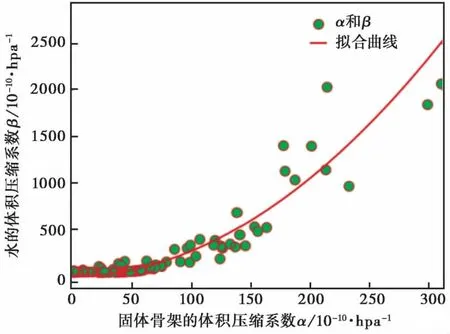
图3 大甸子井含水层体积压缩系数间的关系Fig. 3 The relationship between coefficients of volume compressibility of aquifer for Dadianzi well.

3.3 孔隙度和贮水率的关系

孔隙度和贮水率之间存在明显的幂函数关系， 即Ss=b(1-n)c(c<0)。在第1象限， 孔隙度逐渐增大时， 相应地贮水率也增大(图4)。由于骨架应力减小(固体骨架膨胀或伸长)， 相应地孔隙压力增大(水体压缩)， 单位体积含水层中， 贮存的弹性水量即贮水率随孔隙度的增大而增大。

3.4 孔隙度和渗透系数、 导水系数的关系

由于在不排水状态下的渗透系数仅与M2波频率、 井管半径和贮水率有关， 因此其渗透系数的变化形态和贮水率变化形态非常一致。孔隙度和渗透系数间存在明显的幂函数关系， 即K=b(1-n)c(c<0)。孔隙度逐渐增大时， 相应地渗透系数也增大(图5)。另外， 导水系数为渗透系数和含水层厚度的乘积， 因此其变化形态和渗透系数变化形态也非常一致。孔隙度和导水系数之间亦存在明显的幂函数关系， 孔隙度逐渐增大时， 相应地导水系数也增大(图6)。

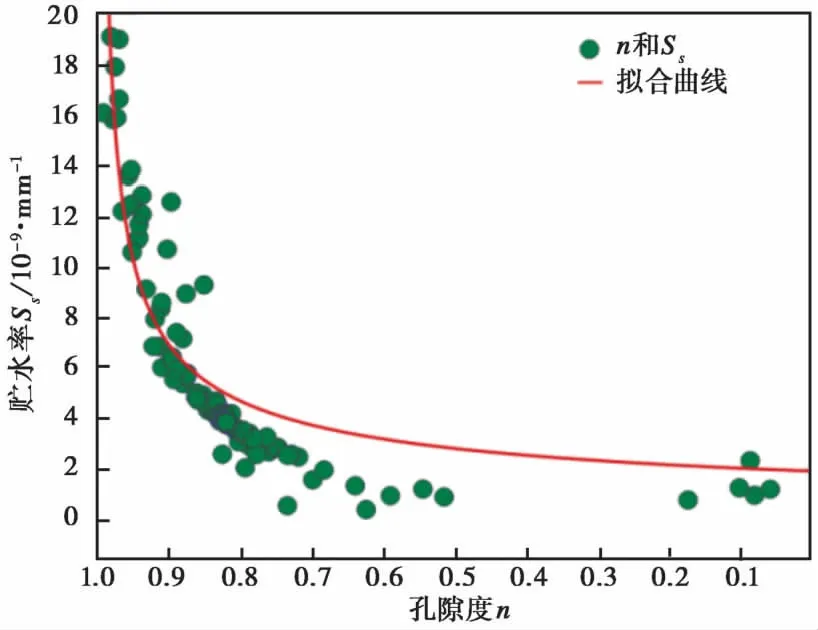
图4 大甸子井含水层孔隙度和贮水率的关系Fig. 4 The relationship between porosity and water storage rate of aquifer for Dadianzi well.

图5 大甸子井含水层孔隙度和渗透系数的关系Fig. 5 The relationship between porosity and permeability coefficient of aquifer for Dadianzi well.

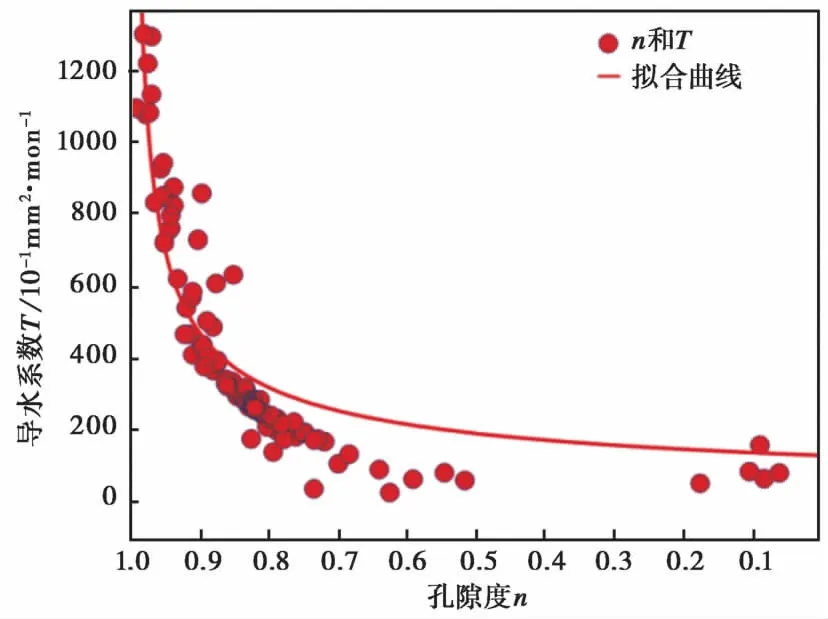
图6 大甸子井含水层孔隙度和导水系数的关系Fig. 6 The relationship between porosity and water conduction coefficient of aquifer for Dadianzi well.

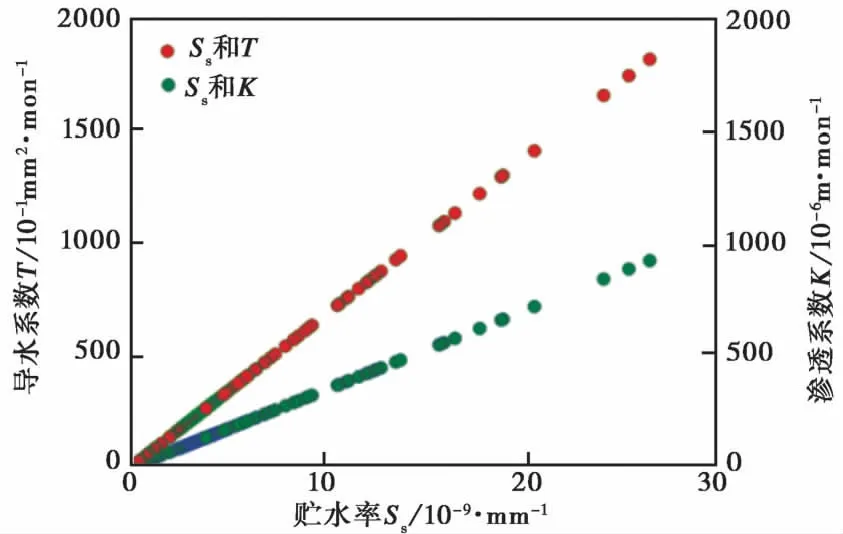
图7 大甸子井含水层贮水率与导水系数、渗透系数的关系Fig. 7 The relationship between water storage rate and water conduction coefficient， permeability coefficient of aquifer for Dadianzi well.

3.5 贮水率和渗透系数、 导水系数的关系

由表1 和图7 可以看出， 不排水状态下渗透系数与贮水率间呈线性关系(线性系数与M2波频率、 井管半径有关)； 导水系数与贮水率间也呈线性关系(线性系数与M2波频率、 井管半径和含水层厚度有关)。即贮水率增大时， 渗透系数和导水系数也相应地呈线性增大。

4 认识与讨论

(1)依据该井的水文地质条件等情况， 该井具有承压水的埋藏条件和特征， 是开展潮汐因子、 气压系数和含水层水文地质参数特征研究的理想观测井。

(2)本文研究的大甸子井含水层的孔隙度， 与固体骨架体积压缩系数和水的体积压缩系数间存在明显的幂函数关系， 其定义域(指孔隙度n)为0～1， 值域(指固体骨架的体积压缩系数为0～-∞； 水的体积压缩系数为0～+∞)， 且幂指数c<0。1)该井含水层介质固体骨架的体积压缩系数随着孔隙度的增大而增大。这归因于， 当孔隙压力增大时， 水的体积减小， 在外应力保持不变的情况下， 骨架应力就会减小， 骨架体积则增大， 并带动孔隙体积一起增大。因此， 当骨架应力减小， 骨架体积增大(膨胀)， 其体积变化量(或变化率)亦越大(易压缩)。因此， 骨架体积压缩系数随着孔隙度的增大而增大。2)当孔隙压力增大时， 水的体积则减小， 其体积变化量(或变化率)亦越小(难压缩)， 则水的体积压缩系数亦减小。同时， 这一过程为孔隙度增大的过程。因此， 水的体积压缩系数随着孔隙度的增大而减小。3)水的体积压缩系数在随孔隙度的增大而减小的过程中， 水的弹性变形越来越小。这是因为， 水的压缩系数越来越小， 其体积变化量亦越小， 水也就越难压缩。与此同时， 固体骨架则表现为易压缩、 弹性变形渐强的过程。

(3)该井固体骨架和水的体积压缩系数之间满足一元二次多项式关系， 且水的体积压缩系数要比固体骨架的体积压缩系数大， 水更易压缩。

(4)大甸子井含水层的孔隙度与贮水率、 渗透系数和导水系数间亦呈明显的幂函数关系。随着孔隙度的增大， 贮水率、 渗透系数和导水系数也相应增大。另外， 随着贮水率的增大， 渗透系数和导水系数也呈线性增大。

(5)与传统的现场抽水试验和室内实验等不同， 本文利用数字化水位等资料， 结合气压系数和维尼迪科夫潮汐调和分析结果， 获取不排水状态下含水层介质的孔隙度、 固体骨架的体积压缩系数、 水的体积压缩系数、 贮水率、 渗透系数和导水系数是简便易行的。当然， 上述研究都是在假设大甸子井含水层介质是线性、 均质和各向同性的弹性体， 井中的水为理想流体， 同时外应力和外观总体积保持不变的情况下完成的。在实际应用过程中还需进行深入研究。

致谢 在本文研究过程中， 得到了中国地震局地壳应力研究所刘耀炜研究员、 中国地震台网中心黄辅琼研究员、 张晶研究员和晏锐等的悉心指导和帮助， 在此一并表示衷心的感谢。

丁风和， 赵铁锁， 尹占军， 等. 2007. 大甸子井水位的气压系数及其震前异常 [J]. 西北地震学报， 29(2): 174—176.

DING Feng-he， ZHAO Tie-suo， YIN Zhan-jun，etal. 2007. Anomaly before earthquakes of air pressure coefficient for Dadianzi well water level [J]. Northwestern Seismological Journal， 29(2): 174—176(in Chinese).

李春洪， 陈益惠， 田竹君. 1990. 井-含水层系统对固体潮的动态响应及其影响因素 [J]. 中国地震， 6(2): 37— 45.

LI Chun-hong， CHEN Yi-hui， TIAN Zhu-jun. 1990. The dynamic response of well-aquifer system to earth tides and its influence factors [J]. Earthquake Research in China， 6(2): 37— 45(in Chinese).

李义昌. 1995. 地下水动力学 [M]. 北京: 中国矿业大学出版社. 179—190.

LI Yi-chang. 1995. Underground Water Dynamics [M]. China University of Mining Technology Publishing House， Beijing. 179—190(in Chinese).

刘序俨， 郑小菁， 王林， 等. 2009. 承压井水位观测系统对体应变的响应机制分析 [J]. 地球物理学报， 52(12): 3147—3157.

LIU Xu-yan， ZHEN Xiao-jing， WANG Lin，etal. 2009. Response analysis of the well-water-level system in confined aquifer [J]. Chinese Journal of Geophysics， 52(12): 3147—3157(in Chinese).

骆鸣津， 杨毅， 李安印， 等. 1990. 地下水水位固体潮的扩散方程及其解 [A]. 见: 中国地球物理学会.1990年中国地球物理学会第六届学术年会论文集. 北京: 地震出版社. 66—76.

LUO Ming-jin， YANG Yi， LI An-ying，etal. 1990. The diffusion equation of groundwater level tide and its solution [A]. In: Chinese Geophysical Society(ed). Proceedings of the 6th Annual Meeting of the Chinese Geophysical Society， 1990. Seismological Press， Beijing. 66—76(in Chinese).

田竹君， 谷园珠. 1985. 地下水微动态资料的分析与处理 [J]. 地震地质， 7(3): 51— 62.

TIAN Zhu-jun， GU Yuan-zhu. 1985. Analysis and processing of data on fluctuations of groundwater level [J]. Seismology and Geology， 7(3): 51— 62(in Chinese).

王礼恒， 李国敏， 董艳辉， 等. 2012. 利用观测孔中地下水位潮汐效应计算天津滨海新区含水层参数 [J]. 水文地质工程地质， 39(4): 7—11.

WANG Li-heng， LI Guo-min， DONG Yan-hui，etal. 2012. Estimation of shallow aquifer parameters using groundwater level tidal fluctuations at two boreholes in a coasta1 aquifer [J]. Hydrogeology and Engineering Geology， 39(4): 7—11(in Chinese).

殷积涛， 汪成民. 1988. 承压含水层的荷载效应和井孔水位的气压效应 [J]. 中国地震， 4(2): 39— 48.

Yin Ji-tao， WANG Cheng-min. 1988. Loading effect on confined aquifer and barometric effect on water level in wells [J]. Earthquake Research in China， 4(2): 39— 48(in Chinese).

张昭栋. 1986. 高阶差分法求深井水位的气压系数 [J]. 地震学刊， (2): 74—78.

ZHANG Zhao-dong. 1986. High-order difference method for deep well water level air pressure coefficient [J]. Journal of Seismology， (2): 74—78(in Chinese).

张昭栋， 郑金涵， 冯初刚. 1989. 井水位的固体潮效应和气压效应与含水层参数间的定量关系 [J]. 西北地震学报， 11(3): 47—52.

ZHANG Zhao-dong， ZHENG Jin-han， FENG Chu-gang. 1989. Quantitative relationship between the earth tide effect of well water level， the barometric pressure effect and the parameters of aquifers [J]. Northwestern Seismological Journal， 11(3): 47—52(in Chinese).

张昭栋， 郑金涵， 张广城. 1995. 水井含水层系统的潮汐响应函数 [J]. 西北地震学报， 17(3): 66—71.

ZHANG Zhao-dong， ZHENG Jin-han， ZHANG Guang-cheng. 1995. Response functions of well aquifer system to tide [J]. Northwestern Seismological Journal， 17(3): 66—71(in Chinese).

Bredehoeft J D. 1967. Response of well-aquifer systems to earth tides [J]. Journal of Geophysical Research， 72(12): 3075—3087.

Davis S N， Dewiest R J M. 1966. Hydrogeology [M]. New York: John Wiley and Sons.

Erskine A D. 1991. The effect of tidal fluctuation on a coastal aquifer in the UK [J]. Groundwater， 29(4): 556—562.

GUI J L， HONG K G， WEI L W. 2013. Transfer functions of the well-aquifer systems response to atmospheric loading and earth tide from low to high-frequency band [J]. Journal of Geophysical Research， 118(5): 1904—1924.

John B， Keith E S， Mousa D S. 1991. Estimating aquifer parameters from analysis of forced fluctuations in well level: An example from the Nubian formation near Aswan， Egypt: 2 Poroelastic properties [J]. Journal of Geophysical Research， 96(B7): 12139—12160.

Kamp G， Gale J E. 1983. Theory of earth tide and barometric effects in porous formations with compressible grains [J]. Water Resources Research， 19(2): 538—544.

Narasinmhan T N， Kanehiro B Y， Witherspon P A. 1984. Interpretation of earth tide response of three deep， confined aquifers [J]. Journal of Geophysical Research， 89(B3): 1913—1924.

Rojstaczer S. 1988. Determination of fluid flow properties from the response of water levels in wells to atmospheric loading [J]. Water Resources Research， 24(11): 1927—1938.

THE CHANGING RELATIONSHIP OF HYDROGEOLOGICAL PARAMETERS OF DADIANZI WELL-AQUIFER SYSTEM

DING Feng-he1)DAI Yong1)SONG Hui-ying2)WEI Jian-min1)CHA Si1)

1)EarthquakeAdministrationofInnerMongoliaAutonomousRegion，Hohhot010010，China2)TransportationInstituteofInnerMongoliaUniversity，Hohhot010020，China

Hydrogeological parameter is an important index to characterize the hydrogeological properties of the aquifer， and has a clear physical basis and mechanism. Although the predecessors have made significant achievements in these areas， research is lacking on the changing law and relationship of the hydrogeological parameters of well-aquifer system.

The digital water level and barometric pressure data of Dadianzi Well are used as the basis in this study. Based on the theories of elastic mechanics， rock mechanics and fluid mechanics， and using barometric pressure coefficient and tidal factor， the hydrogeological parameters in Dadianzi well-aquifer system in undrained conditions are studied. The corresponding water storage rate can also be obtained quantitatively. In addition， with the thickness of the aquifer， the pressure transmitting coefficient， the radius of the well and the frequency of the tidal wave， the permeability coefficient and transmissibility coefficient of well-aquifer system can be obtained， and the relationships between them are derived.

The results show that: 1)There is an obvious power function relationship between porosity and solid skeleton volume compression coefficient， volume compression coefficient of water in aquifer， water storage rate， permeability coefficient and transmissibility coefficient. The volume compression coefficient of solid skeleton， water storage rate， permeability coefficient and transmissibility coefficient have a positive correlation with the porosity， the volume compression coefficient of water in aquifer decreases with increasing porosity. The volume compression coefficient of solid skeleton and water in aquifer can be well fitted to one of two quadratic polynomials. And the volume compression coefficient of water in aquifer is larger than the solid skeleton volume compression coefficient， water is more easily compressed. In addition， with the increase of water storage rate， the permeability coefficient and transmissibility coefficient also increase linearly; 2)Different from the traditional pumping test and indoor experiment， this paper uses the digital water level and other data， combined with the pressure coefficient and Venedikov tidal harmonic analysis results to access to the porosity， the volume compression coefficient of solid skeleton and water in aquifer medium， water storage rate， the permeability coefficient and the transmissibility coefficient. This method is simple and accurate.

Dadianzi well， artesian well-aquifer system， hydrogeological parameters， undrained condition

10.3969/j.issn.0253- 4967.2015.04.004

2015-07-21收稿， 2015-10-08改回。

中国地震局监测预报司震情跟踪定向工作任务(2014010301)资助。 *通讯作者： 戴勇， 男， 工程师， 电话： 0471-6510797， E-mail: daiyong06@mails.ucas.ac.cn。

P315.2

A

0253-4967(2015)04-0982-09

丁风和， 男， 1977年生， 2005年于中国地震局兰州地震研究所获硕士学位， 高级工程师， 研究方向为地震地下流体， 电话： 0471-6512438， E-mail： dingfenghe@126.com。