锻造液压机高强度特殊螺纹拉杆有限元仿真分析
2015-07-01毛春燕解文科吴瀚崚
毛春燕,解文科,吴瀚崚
(1.太原重工股份有限公司 技术中心,山西 太原030024;2.哈尔滨工业大学(威海),山东 威海264200)
锻造液压机是金属压力加工制造业中广泛应用的关键设备,圆形拉杆(又称“ 张力柱”)是液压机中最重要的零件。工作中,拉杆承受满吨位的轴向拉力,长期处于大幅值的单向交变拉应力状态;承受由于上、下横梁变形而作用于固定螺母处的角弯矩载荷作用;同时,拉杆还作为活动横梁的导向体,在偏心锻造时,承受活动横梁的横向推力和弯矩。因而,拉杆成为液压机机架中最易破坏的关键零件,发生断裂的例子屡见不鲜。断裂和损坏的部位大多处于拉杆在下横梁上平面与固定螺母结合部位的螺纹根部,断口具有疲劳破坏特征。
现有的液压机拉杆普遍采用顶角为45°锯齿螺纹,如图1 所示,齿根圆角半径很小,计算机三维有限元分析结果表明[1-3],齿根圆角应力集中现象非常严重,甚至超过了材料的屈服强度,导致拉杆的抗疲劳强度大大降低,成为拉杆频繁断裂的主要原因之一。而且,随着装备制造业逐步大型化的发展,超万吨的压机越来越多,拉杆螺纹承受的力也不断增大,仅通过不断加大拉杆螺纹直径效果十分有限。因此,急需设计一种低应力螺纹拉杆,以解决锻造液压机拉杆频繁断裂问题,延长拉杆使用寿命。
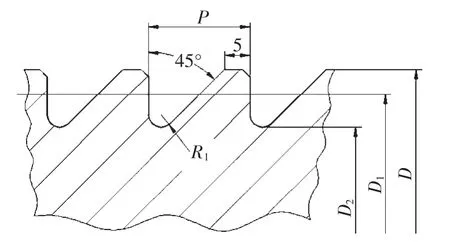
图1 45°锯齿螺纹牙型
本文提出一种低应力高强度螺纹型式,用于消除现有锻造液压机拉杆螺纹的应力集中现象,延长拉杆的使用寿命。
1 传统拉杆螺纹牙强度计算方法
目前,对螺纹牙强度的计算,一般仍沿用将螺纹牙展开当作一个悬臂梁、并假设载荷在螺纹牙表面平均分布, 用作用在螺纹牙高度中点的一个集中力来代替的方法,求其根部危险断面上的应力值。
现将一般工程上螺纹强度计算方法说明如下。作用在每一圈螺纹上的力:

式中:p2——立柱所受总拉力;
n——立柱数目;
工作螺纹圈数Z 并不好确定,根据使用经验一般只能保守假设前3、5 扣受力。后文的有限元计算证实这种假设可行,同时可清楚看到螺纹牙受力呈逐渐递减趋势。
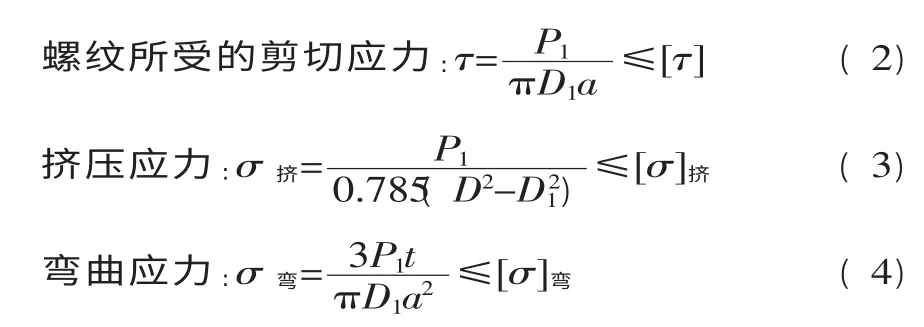
式中:a—螺纹牙根部宽度;
D—螺纹外径;
D1—螺纹内径。
用以上方法计算的螺纹强度因为有很多假设,很难真实反映螺纹的应力水平。
2 新型拉杆高强度螺纹牙型
新型拉杆采用高强度螺纹,拉杆与螺母的螺纹配合一致使用同一台机床加工。多种规格的拉杆已在工程实际中应用,在经过多次优化设计后得出基本参数的公式。
如图2、图3 所示为锻造液压机设计的新型螺纹牙型。拉杆的外螺纹与内螺纹具有如下特征:与传统的45°锯齿形螺纹不同,拉杆的外螺纹与内螺纹的原始三角形顶角的角度θ 相对较大,远大于45°,该角度θ 可以选取在55~65°之间,且以60°为优选;外螺纹及内螺纹的螺距P 相对较大。此外,外螺纹与内螺纹的根部均为一圆弧。外螺纹的根部圆弧半径R 大于内螺纹的根部圆弧半径r。
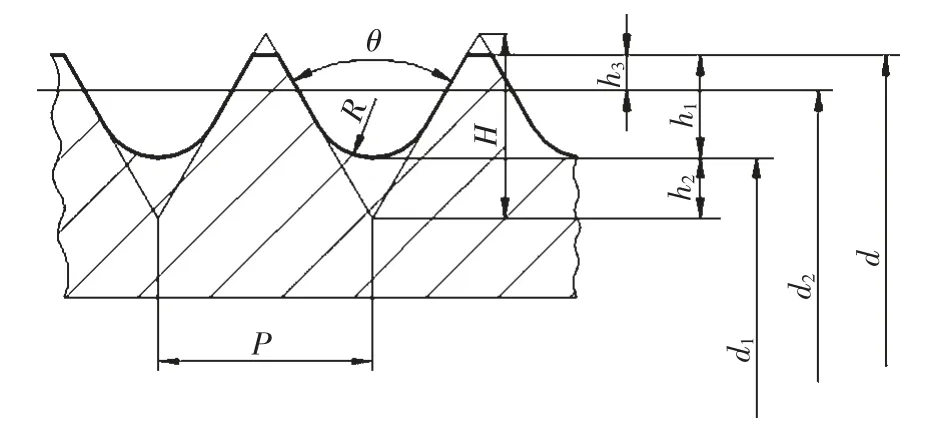
图2 新型拉杆螺纹牙型
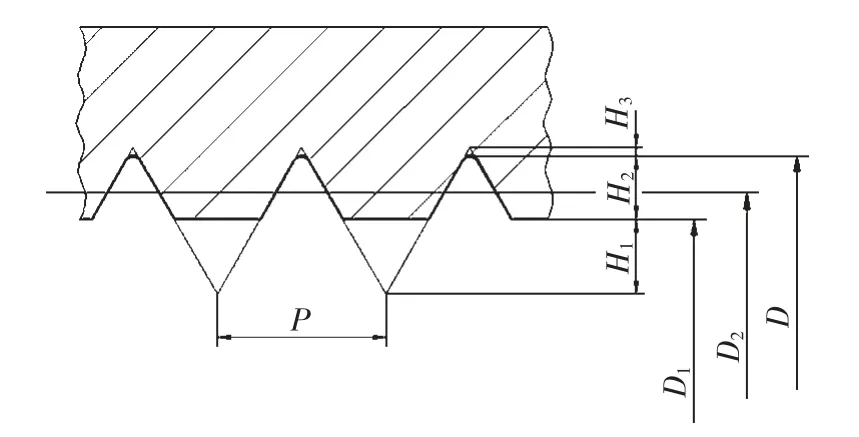
图3 新型螺母螺纹牙型
如图2 所示对拉杆的螺纹进行分析,外螺纹的基本参数包括:螺距P,原始三角形的顶角θ,外螺纹根部圆弧的半径R,以及外螺纹的大径d,外螺纹根部圆弧相切于外螺纹的原始三角形的两腰。结合图3 可以看到,内螺纹的基本参数包括:螺距P,原始三角形的顶角θ,内螺纹根部圆弧的半径r,以及内螺纹小径D1,内螺纹根部圆弧相切于内螺纹的原始三角形的两腰。
其中,螺距P 的取值与外螺纹的大径d 有关,d较大者,则螺距P 也应较大。在某一限定尺寸范围内,螺距P 的取值约为外螺纹大径d 的6.5%~8%。例如,对于d=150mm~190mm 的螺杆,螺距P 可选取10mm~15mm,考虑到便于实际生产,可统一选取一较佳值P 为12mm; 对于d=200~260mm 的螺杆,螺距P 可选取13mm~20mm,且可统一选取一较佳值P为16mm。
根据上述的基本参数,就能够计算得出外螺纹及内螺纹的规格参数。包括:外螺纹的原始三角形高度H,外螺纹的牙齿高度h1,外螺纹的牙根高度h2,外螺纹的牙顶高度h3,外螺纹的中径d2和小径d1;内螺纹的原始三角形的高度H,内螺纹的牙齿高度H1,内螺纹的牙根高度H2,内螺纹的牙顶高度H3,内螺纹的大径D,中径D2和小径D1。
根据上述设计,由于增大了内螺纹和外螺纹的螺距P 及原始三角形的顶角θ,使得外螺纹及内螺纹的接触面增大,因而能有效减小螺纹所受应力。此外,由于设计增大了外螺纹的根部圆弧半径,能进一步减小外螺纹根部应力集中现象,延长螺杆的寿命。
3 新型拉杆高强度螺纹有限元计算
基于I-DEAS 有限元分析软件建立真实工况力学模型,采用接触算法进行分析计算。以M240 的螺纹为例,通过拉杆与螺母的接触分析能清晰地看到45°锯齿形螺纹和新型高强度螺纹在受力后的应力大小及分布。

图4 45°锯齿螺纹拉杆与螺母接触分析模型图
3.1 模型建立
查标准JB/ZQ4723液压机用45°锯齿螺纹牙型与基本尺寸[5],选用YS240×8,按标准尺寸建立拉杆和螺母的模型如图4 所示。
采用上面工程实例中计算公式得到M240×16 新型螺纹拉杆和螺母的详细尺寸建立有限元模型如图5 所示。

图5 新型高强度螺纹拉杆与螺母接触分析模型图
以上建立的两个有限元分析模型拉杆和螺母的直径大小相等,但螺纹部分的区别十分明显,图4 啮合的螺纹牙大约是28 对,而图5 啮合的螺纹牙数大约是14 对。也正是这种区别使得这种新型螺纹具有了承受高强度的能力。
3.2 网格划分
由于拉杆属于轴对称件,为缩短计算时间,两个模型都取1/4 计算;且螺纹牙型部位尺寸细小,为体现出主要受力部分的应力应变,运用I-DEAS 中分离命令将拉杆与螺母螺纹部位分离出来,螺纹牙型局部网格细化如图6、7 所示。

图6 45°锯齿螺纹模型网格图

图7 新型螺纹模型网格图
3.3 计算结果分析
根据在液压机上使用的实际工况,建立以下边界条件:①载荷边界条件,拉杆两端部施加拉力,螺母一端部施加压力;②接触边界条件,拉杆螺纹面与螺母螺纹面建立接触对,设置接触探测距离及接触面之间的摩擦系数;③约束边界条件。求解之后计算结果如图8、9、10、11 所示。
从应力图中可清楚看到,45°锯齿螺纹拉杆最高应力为538MPa,螺母最高应力424MPa;而新型螺纹的拉杆最高应力为294MPa,螺母最高应力308MPa。充分证明新型螺纹拉杆的优势。

图8 45°锯齿螺纹拉杆应力图

图9 新型螺纹拉杆应力图

图10 45°锯齿螺纹螺母应力图

图11 新型螺纹螺母应力图
由图8 可看到,45°锯齿螺纹的拉杆上第一扣应力最高538MPa,第二扣约为450MPa,第三扣约为365MPa,第四扣约为281MPa,由此可见应力高值主要集中在前面3~5 扣(这也验证了前面45?锯齿螺纹强度计算中假设3~5 扣受力的合理性),随后应力值迅速递减,大约到整个啮合螺纹长度的一半时,应力值就递减到约127MPa,直至啮合终了应力值递减为24.7MPa。
由图9 可以看到新型螺纹的拉杆在前6 扣应力值从294MPa 递减到168MPa,应力值递减缓慢,应力高值占了整个啮合螺纹长度大约一半,直至啮合终了应力值缓慢递减为61.8MPa。
图10、11 的螺母应力图也显著表示出二者之间受力的差异。说明由于新型螺纹特殊的牙型使得拉杆啮合部位的螺纹牙受力趋于均匀,大大改善了普通螺纹由最初啮合3~5 扣齿受力状况,降低拉杆螺纹应力45%,消除了高应力集中现象。
4 结论
本文给出了新型螺纹牙型的详细参数设计方法,然后采用有限元的接触算法,结合实际工况,避免传统计算方法的假设过多状况,通过细化螺纹部位网格,计算并比较了两种不同螺纹时拉杆和螺母的应力,真实且直观地反映了各自受力状况。说明新型螺纹的拉杆通过增大螺纹的螺距及原始三角形的顶角,以及螺杆螺纹的根部圆弧半径,能有效降低螺纹应力,使螺纹的受力更均衡,提高了拉杆的承载能力和可靠性。从而使拉杆螺纹不会发生研死粘合现象,便于安装且使用寿命长。
[1]钱学毅,吴 双.锯齿型螺纹牙根应力有限元分析[J].起重运输机械,2008,(9):74-76.
[2]白卫卫,等.螺母外形结构对螺栓疲劳强度的影响[J].机械研究与应用,2004,17(6):27-28,30.
[3]方 栋,陈继志.高强度螺栓螺纹根部应力集中的有限元分析[J].材料开发与应用,2007,22(2):37-39.
[4]何彦忠,黄建民,仲 君,等.压力机闭式组合机身有限元分析及补强拉杆预紧设计新方法[J].锻压装备与制造技术,2012,47(5):29-32.
[5]中国重型机械工业协会.重型机械标准(第2 卷)[M].昆明:云南科技出版社,2008.
[6]刘红梅,李永堂,齐会萍,等.螺纹冷滚压参数化造型与有限元分析[J].锻压装备与制造技术,2011,46(2):78-81.
[7]公制、美制和英制螺纹标准手册编委会编著.公制、美制和英制螺纹标准手册[M].北京:中国标准出版社,2004.
[8]薛 强,苗德华.钢轨接头螺栓的有限元应力集中分析[J].铁道标准设计,2004,(4):70-72.
[9]刘芳辉,袁剑雄.锯齿形螺纹作用中径计算[J].哈尔滨电工学院学报,1996,19(3):358-361.
[10]李明民,译.螺纹结构强度设计规范.高压技术,1984,21(1).
[11]张德驺.螺纹牙强度研究[J].哈尔滨船舶工程学院学报,1986,7(4):80-93.
