细长压杆失稳理论对一级台阶凸模的设计指导
2015-07-01董冠文李宗义朱七二
董冠文,李宗义,朱七二
(甘肃机电职业技术学院,甘肃 天水741001)
0 引言
众所周知,冲裁凸模作为冷冲模重要的工作零件之一,始终受到模具设计人员的重视。本文拟采用细长压杆失稳理论,分析一级台阶凸模在冲裁过程中的受力特点,将台阶凸模刃口长度部分视为弹性杆,其余部分视为刚性杆,建立了弹性和刚性的混合杆系的力学模型,进而将问题转化为一阶常微分方程的初值问题,用4 阶经典Rung-Kutta 法,计算弹性和刚性的混合杆系的力学模型的数值解,进而获得随一级台阶凸模的弹性长度与刚性长度之比的大范围变化的载荷参数的关系曲线。
1 弹性和刚性的混合杆系的力学模型建立
1.1 凸模的结构组成
以图1 所示圆台阶凸模为例,结合冲模术语国家标准,圆凸模的结构组成要素如下:①头部,即直径最大的圆柱部分;②头厚,即头部的厚度;③头部直径,圆锥头时为最大直径;④连接半径,防止应力集中;⑤杆,为凸模与固定板孔配合部分;⑥杆直径,一般与固定板孔为H7/m6 配合;⑦引导直径,可略小于杆直径,便于压入固定板;⑧过渡半径,光滑连接刃口直径与杆直径;⑨刃口直径,圆凸模直径尺寸;⑩过渡圆角,光滑连接刃口直径与杆直径;⑪刃口长度,包括切入材料的深度和刃磨长度;⑫凸模总长度,简称凸模总长。
1.2 一级台阶凸模的控制方程
现考虑一外形结构如图1 所示的一级台阶凸模,各截面皆为圆形,刃口截面直径⑨为d1,引导直径⑦为d2,头部直径为d3,凸模总长度⑫为l+a,其中刃口⑪与过渡半径⑧总长度为l,头厚②、连接半径④、杆⑤总长度为a,且满足l=6a,凸模工作时,刃口⑪深入板料,此时刃口最容易失稳变形,其余部分相比变形较小,可忽略不计。依据细长压杆失稳理论,将刃口⑪及其过渡部分⑧看成弹性杆,其余部分看成刚性杆,建立了如图2 所示的弹性与刚性混合杆系的力学模型,AC 段为细长弹性杆,弯曲刚度为EI,长度为l,CB 段为刚性杆。在冲裁过程中,相当于施加一微小的侧向干扰F,使弹性杆AC 微弯,刚性杆CB 微偏转[4]。

图1 圆台阶凸模的结构组成
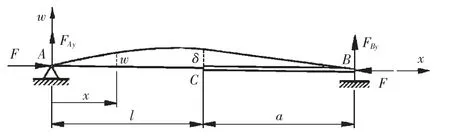
图2 弹性与刚性混合杆系的力学模型示意图
FBy=FAy=0
设截面x 的挠度为w,则杆AC 段的弯矩方程为
M(x)=-Fw
由此得该杆段的挠曲线的微分方程为
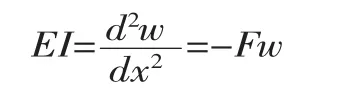
其通解为

设截面C 的挠度为δ,则该截面的转角∠B 大小为
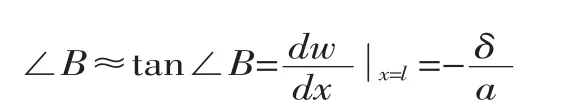
在x=0 处,w=0,代入式(1)得B=0
在x=l 处,w=δ 代入式(1)得
《孟子》云:“天下之本在国,国之本在家,家之本在身。”即个人是家庭的基础,家庭是社会和国家的基本细胞,而婚恋则是个体发展、家庭延续乃至国家生生不息的必要前提和基础。但在现实中,许多贫困农村的男青年遥望着“围城”内的生活,却因种种现实和自身的原因而无法走进婚姻的殿堂。


由(2)得

将(4)代入(3)得

特征根方程(5)就是临界载荷所应满足的方程。
2 数值方法及结果
特征根方程(5)是含有正切三角函数的超越方程, 无法求出其显式解析解,这里采用4 阶经典Rung-Kutta 法求其数值解[5]。
引入无量纲量
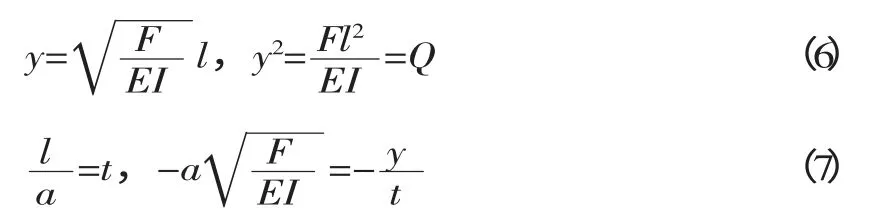
将(6)、(7)代入(5)得

由(8)得

当t=0 代人(9)得

(10)就是(9)的初值。现对(9)取一阶导数得

于是(10)和(11)构成如下一阶常微分方程的初值问题
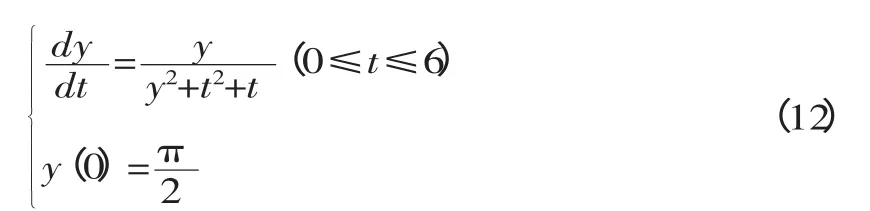
取步长h=0.01,已知t0=0 则tn=t0+nh=nh 阶经典Rung-Kutta 法为

通过计算结果的原始数据,得到了图3 一级台阶凸模无量纲载荷参数与其弹性长度刚性长度比的关系,图3 反映了随着一级台阶凸模其弹性长度刚性长度比的增大,其临界载荷增大,凸模越不易失稳,因此将直通式凸模改造成一级台阶凸模是合理的。也可以依据图3 推测并确定,当t→∞时,y→π,Q→π2,此时不难得到同时由初值得,当于是凸模的冲裁力范围为进而确定凸模刃口长度范围为不难确定凸模长度。在本例中t=6,所以进而确定凸模刃口长度范围为这样一来,既确定了凸模长度的下限,又确定了凸模长度的上限。
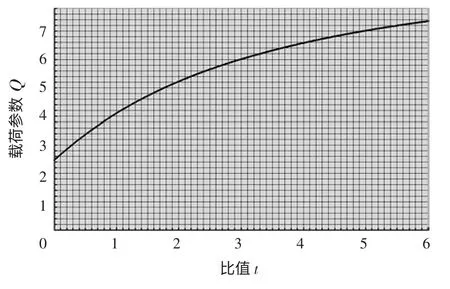
图3 载荷参数与长度比的关系(0≤t≤6)
图4 反映了一级台阶凸模无量纲载荷参数与其刃口长度刚性长度比的关系局部近似于线性弹簧的线性关系,主要是由于一级台阶凸模刚性长度部分被先确定不轻易改变,而后确定凸模刃口长度,在调整凸模长度尺寸时,首先调整凸模刃口长度,这样就导致凸模刃口长度大小往往会影响一级台阶凸模的刃口长度刚性长度比大小,局部呈线弹性关系。
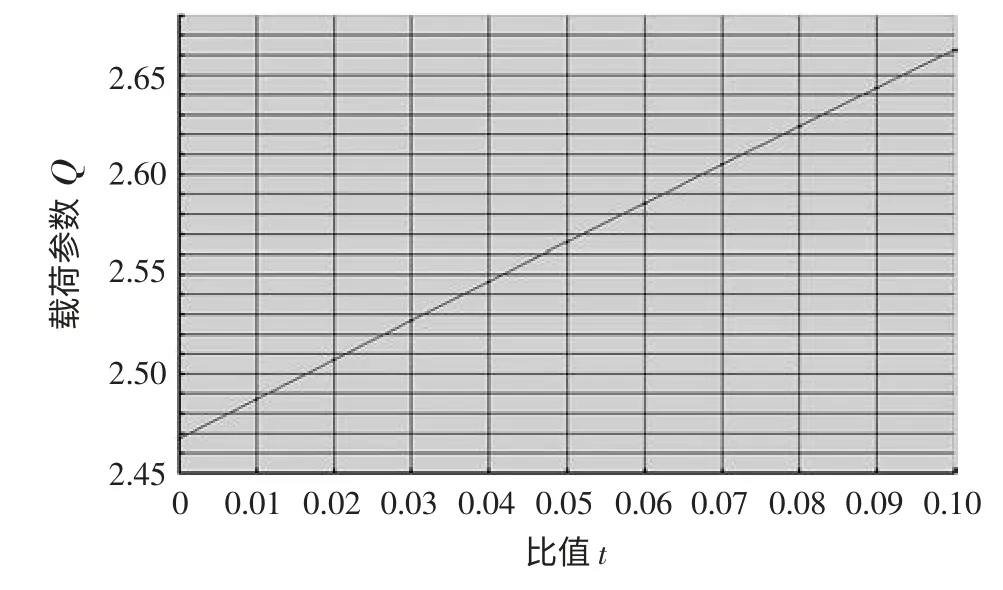
图4 载荷参数与长度比的关系局部放大图(0≤t≤0.1)
图5 反映了随着一级台阶凸模其刃口长度刚性长度比的增大,一级台阶凸模刃口长度系数减小的特征。由此可推测并确定,当t→∞时,μ→1,一级台阶凸模相当于两端铰支的压杆。当t=0 时,μ=2,一级台阶凸模相当于一端固定、另一端自由的压杆。在本例中,当t=6 时,μ=1.1586 一级台阶凸模介于两端铰支的压杆和一端固定,另一端自由的压杆之间的支撑结构。
3 结论

图5 长度系数与长度比的关系(1≤t≤6)
本文依据细长压杆失稳理论,通过对一级台阶凸模的校核方法的改进研究,提出了校核凸模长度需先确定凸模刃口的长度范围的观点,指出了传统校核方法将凸模长度与凸模刃口长度混为一谈进行校核是不合理的。首次采用4 阶经典Rung-Kutta法,计算了弹性和刚性的混合杆系的力学模型的数值解,确定了一级台阶凸模刃口长度的上限和下限,对一级台阶凸模的设计具有一定参考价值。
[1]卢险峰.冲压工艺模具学[M].北京:机械工业出版社,2014.
[2]卢险峰.模具学导论[M].北京:化学工业出版社,2007.
[3]么廷先.台阶凸模的稳定性[J].模具工业,1990,(8):2~7.
[4]单辉祖.材料力学——问题、例题与分析方法[M].北京:高等教育出版社,2006.
[5]关 治,陆金甫.数值方法[M].北京:清华大学出版社,2005.
