圆环镦粗分流面变化规律的探讨
2015-07-01钟志龙程培元朱兴元胡一博
钟志龙,程培元,朱兴元,胡一博
(武汉理工大学 材料科学与工程学院,湖北 武汉430070)
1 前言
很多塑性成形工序,如圆环镦粗、垫环镦粗、开式模锻等,由于金属可能朝多个方向流动,因此总存在一个分流面。其显著特征是径向速度为零,该面以内的金属向内流动,该面以外的金属向外流动[1]。分流面的形状和位置在不同成形瞬间是变化的,使其变形工艺和形状尺寸精度难以控制。确切掌握工艺参数对分流面形状和位置的影响对于预测缺陷成因、控制产品质量、设计预毛坯形状和尺寸、设计成形工序等都具有很大的实际意义[2]。
本文通过研究圆环镦粗来分析分流面的形状和位置的变化规律,众所周知,随工艺参数的变化其分流面可在实体内或实体外。对分流面的分析常用的方法有解析方法、数值方法和实验方法。理论法是在较多的简化和假设前提下进行的,且只能分析分流面位置变化情况,在众多的理论法中变形功法得到许多学者的青睐,它可以分析分流面在实体内或实体外的变化情况。数值方法在金属塑性成形方面获得了越来越多的应用,它可以分析分流面形状和位置的变化,但当分流面在实体外时却无能为力。实验方法虽然结果可靠,但不能确定分流面的形状和位置,故难以满足研究和分析的需要[3]。尽管众多学者关于圆环镦粗过程变形规律开展了大量研究工作,但多是针对具体工艺进行的或者只是简单描述分流的现象[4-6],而对圆环镦粗分流面形状和位置的变化规律缺乏深入的研究和总结。针对以上不足,本文作者通过数值方法并结合变形功法对圆环镦粗过程分流面的变化进行定量分析,得出了一些规律,对控制塑性金属流动的过程有一定的理论和实际意义。
2 研究方案
2.1 有限元模型建立
考虑到圆环压缩变形的轴对称性,采用有限元软件Deform-2D 对成形过程进行模拟,同时为了合理地将模型简化又提高计算精度,仅取坯料子午面的一半作为模拟研究对象,有限元模型如图1 所示。
2.2 有限元分析模拟条件
由于影响圆环镦粗分流面形状和位置的因素较多,通过改变要分析的参数,同时固定其他所有参数值进行模拟。本文通过摩擦因子m、压下量ε=△H/H(△H—圆环高度变化量,H—圆环初始高度)、形状因子λ=2H/(D-d)(D—圆环外径、d—圆环内径)等工艺参数对圆环镦粗分流面形状和位置的影响进行研究。为防止镦粗过程中圆环因坯料过高而发生失稳,通常情况下λ 不大于3.0,最大压下量为50%。模拟过程中不考虑上下模板的变形,模具属性为刚性体,坯料选用纯铝作为理想刚塑性模型材料。成形速度为1mm/s,坯料和模具的温度均为常温,模具与坯料间摩擦边界条件按常剪切因子摩擦模型施加。
3 模拟结果分析
3.1 摩擦因子m对分流面形状和位置的影响
图2 所示压下量ε=30%,形状因子λ=4/3(D=60,d=30,H=20),摩擦因子m 分别为0.1、0.173、0.4条件下圆环镦粗变形过程中分流面形状和位置分布图。由图2a,当m=0.1 时,分流面在实体外,金属全部向外流动,通过外推法可以求出此时的理论分流面的分布图,分流面在截面上并不是直线而是呈中部内凸有一定弧度的曲线。当m=0.173 时(图2b),分流面一部分在实体内,一部分在实体外,近似认为分流面与圆环内径重合,分流面位置外移。当m=0.4时(图2c),分流面全部在实体内,金属向分流面两边流动,且分流面在截面上呈中部外凸的曲线,分流面位置继续外移。当摩擦因子增加到一定值时,圆环内径向内增加的位移大于分流面向外增加的位移,分流面可能内移。
由于分流面和内径的截面都是带有一定弧度的曲线,为了便于分析分流面的位置变化规律,对其求平均值,按直线处理。图3 所示为λ=4/3,在不同的压下量下,分流面半径R分与内径r内的比值随摩擦因子m 的变化图。从图中可以看出,在不同的压下量下R分/r内都是随着摩擦因子的增大而增大,在虚线以下R分/r内小于1,随摩擦因子m 增大的比较迅速,此时分流面半径小于圆环内径,但与圆环内径的距离越来越小。在虚线上时R分/r内=1,此时分流面与圆环内径重合,所以在不同的压下量下存在分流面与圆环内径重合的摩擦因子分界点,通过计算发现临界摩擦因子m 值随压下量的增大而减小,如表1 所示。在虚线以上R分/r内大于1,此时分流面半径大于圆环内径,R分/r内随摩擦因子增大而增加的较缓慢,但与圆环内径距离越来越大。通过数据拟合发现,在不同压下量下,R分/r内与摩擦因子的关系符合指数模型y=y0+A1ex/t1+A2ex/t2。
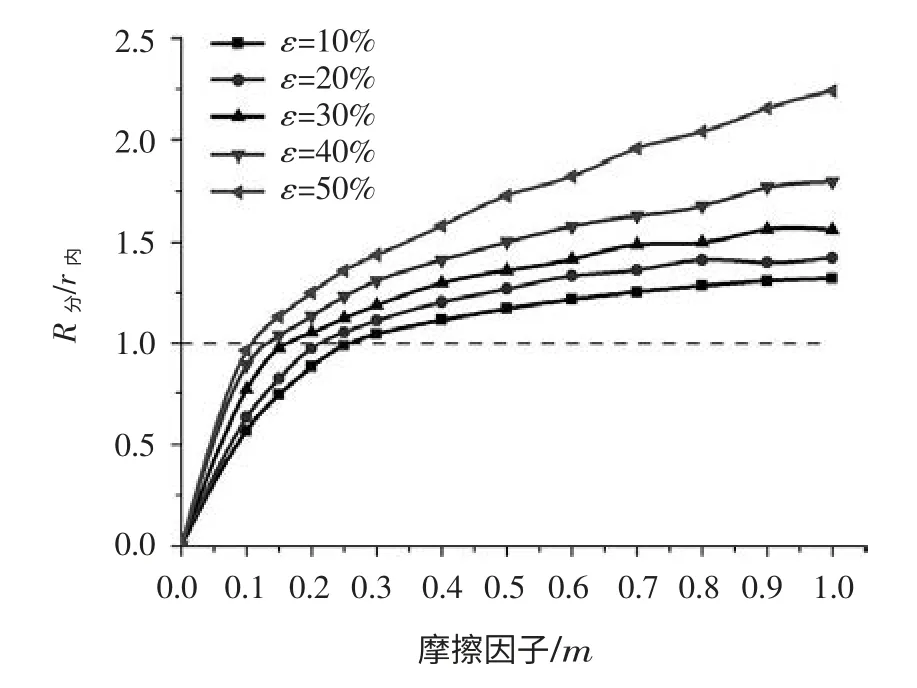
图3 不同压下量下R 分/r 内随摩擦因子变化图
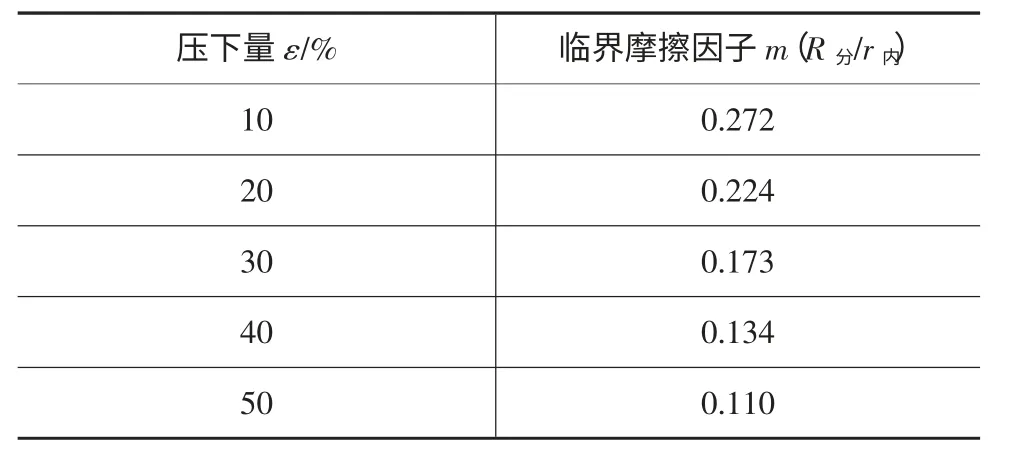
表1 不同压下量下临界摩擦因子m
3.2 压下量ε对分流面形状和位置的影响
图4 所示为摩擦因子m=0.2、形状因子λ=4/3(D=60,d=30,H=20)、压下量ε分别为10%、23.7%、50%条件下圆环镦粗变形过程中分流面形状和位置的分布图。由图4a,当压下量ε=10%时,分流面在实体外,金属全部向外流动,通过外推法可知分流面在截面上呈中部内凸曲线。当压下量ε=23.7%时(图4b),分流面近似与圆环内径重合,分流面位置外移。当压下量ε=50%时(图4c),分流面全部在实体内,金属向分流面两边流动,且分流面在截面上呈中部外凸的曲线,分流面位置继续外移。当压下量增加到一定值时,圆环内径向内增加的位移大于分流面向外增加的位移,分流面可能内移。

图4 不同压下量ε时分流面形状和位置分布图
图5 所示为形状因子λ=4/3、在不同摩擦因子下,R分/r内随压下量ε的变化图。由图可知不论摩擦因子为何值,R分/r内总是随着压下量的增大而增大。在虚线以下R分<r内,表示分流面在实体外,且随压下量的增加R分离r内越来越近;虚线上R分=r内,分流面与圆环内径重合,此时存在一个临界的压下量,在不同的摩擦因子下有不同的临界压下量,且随着摩擦因子的增大而减小,如表2所示;在虚线以上R分>r内,表示分流面在圆环中,且随压下量的增加R分离r内越来越远。从图还可以看出,当摩擦因子m 小于等于0.1,压下量最大不超过50%时,随压下量增加分流面始终在实体外;当摩擦因子m 在0.1~0.3时,压下量较小时分流面在实体外,压下量较大时在实体内;当摩擦因子m 大于等于0.3 时,随压下量增加分流面始终在实体内。

图5 不同摩擦因子下,R 分/r 内随压下量的变化图
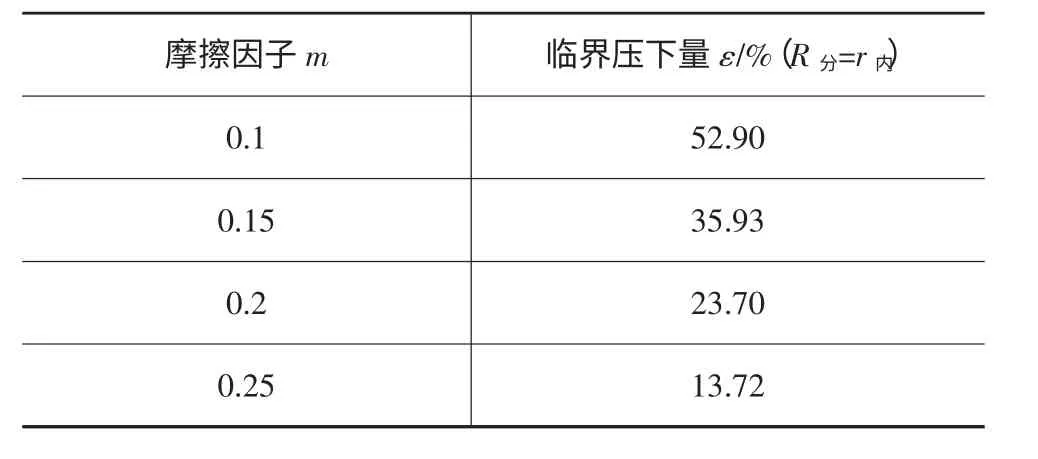
表2 不同摩擦因子m 下的临界压下量ε
3.3 形状因子λ对分流面形状和位置的影响
根据定义可知,形状因子与圆环内外径、初始高度有关,为便于对比分析,固定内外径,通过改变坯料高度H 值来获得不同的形状因子λ。为了考虑内料高度H 值来获得不同的形状因子λ。为了考虑内径的影响,设定圆环内径d 分别为20、30、40 的情况下,改变圆环高度H 使形状因子为1.2、1.6、2.0、2.4、2.8。通过数值模拟分析可知,随着形状因子的增加分流面在截面上同样是由中部内凸曲线、近似直线、中部外凸曲线之间转变,且分流面的位置逐渐内移。图6 所示为m=0.4、压下量ε=50%、R分/r内随形状因子λ的变化图。由图可知,在不同的圆环内径下,R分/r内都随形状因子λ的增大而减小,表明分流面越来越靠近圆环内径,但分流面半径一直大于圆环内径。从图还可知,当形状因子一定时,R分/r内随初始圆环内径的增大而减小,分流面越靠近圆环内径。

图6 R 分/r 内随形状因子λ 的变化图
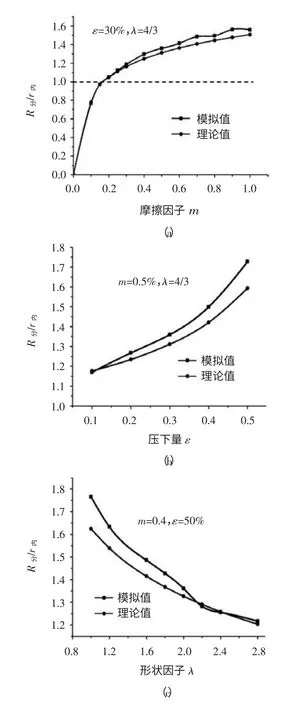
图7 为R 分/r 内随工艺参数变化的对比图
4 理论验证
本文通过变形功法得出R分/r内与各工艺参数变化关系,并与模拟值进行对比。图7 为R分/r内随工艺参数变化的模拟值和理论值的对比图,模拟值与理论值基本一致,证明了模拟值的可靠性。
5 结论
(1)通过数值分析发现分流面在截面上的形状并不是一条直线,而是呈中部内凸/外凸曲线、近似直线三种状态;分流面的位置随着摩擦因子m、压下量ε的增加先右移后左移;随着形状因子λ 的增加逐渐左移。
(2)分流面半径与圆环内径的比值R分/r内随着摩擦因子m、压下量ε的增大而增大;随着形状因子λ 的增大而减小。当R分/r内<1 时,分流面在实体外,该值越小,分流面离圆环内径越远;当R分/r内=1时,分流面与圆环内径重合;当R分/r内>1 时,分流面在实体内,该值越大,分流面离圆环内径越远。因此,以圆环内壁为参照,分流面的变化过程为先靠近圆环内壁,再与之重合,最后远离圆环内壁。
[1]邰清安,李晓光,李治华,等.应用FEM 与圆环镦粗实验测定TC4 钛合金高温变形时的摩擦因数[J].材料工程,2011,(6):23-31.
[2]胡积威,董定福,王树军,等.分流面位置的模拟研究[C]//1995 中国机械工程学会锻压学会第六届学术年会.北京:1995.
[3]李 峰.盘类件模锻过程金属变形模式及流动规律研究[D].哈尔滨:哈尔滨工业大学,2007.
[4]惠媛媛,唐文亭,袁中岳.圆环在平板间镦粗变形规律的数值模拟[J].铸造设备研究,2005,(1):34-36.
[5]赵英亮,梅瑞斌,包 立,等.7075 铝合金环压缩过程摩擦影响的有限元分析[J].锻压装备与制造技术,2013,48(3):89-93.
[6]惠媛媛.圆环镦粗过程数值模拟应力场研究[J].锻压装备与制造技术,2010,45(1):90-92.
