氢原子能级Stark位移的理论研究

樊 娟，李小勇*，王文海

(西北民族大学实验中心，甘肃兰州 730030)

氢原子能级Stark位移的理论研究

樊 娟，李小勇*，王文海

(西北民族大学实验中心，甘肃兰州 730030)

利用对角化方法，通过数值求解氢原子处于静电场中薛定谔方程，研究了氢原子的Stark能级分裂，计算得到了n=7,10,15,16,17,18能级附近的Stark位移.

Stark位移;氢原子;对角化

氢原子中电子受到对称的库仑场的作用，第n个能级有n2重简并.当氢原子处在外电场中时，电子所受势场的球对称性受到破坏，能级发生移动或分裂，简并度降低.这种在外电场中氢原子能级发生移动或分裂的现象，称之为氢原子的Stark效应.Stark效应的发现，证实了玻尔氢原子理论模型的正确性，为早期量子力学的发展提供了一定的实验支持，并开启了人们研究原子与外场相互作用的大门，并且Stark效应对于理解原子或者分子光谱等也具有非常重要的意义.

Stark效应发现后,人们对其产生了浓厚的兴趣.理论上已发展了好几种研究Stark位移的方法，最常用的有微扰法、解析法(或半解析法)和直接数值求解法.时庆云[1]对氢原子一级Stark效应进行了研究，并讨论了n=1,2,3三个能级.曾谨言[2]同样也对氢原子的一级Stark效应进行了研究.许新胜等[3]研究了氢原子低能级的Stark效应，基态精确到了二级修正.苏燕飞等[4]给出了任意状态下氢原子Stark效应中的久期方程行列式中各矩阵元的分布规律，并给出了n=1，2，3，4能级对应的久期方程.这些研究都采用了微扰法.用微扰法研究氢原子的Stark位移时，当氢原子处于弱外电场下且研究的为高激发态时，计算得到的结果能与实验符合很好，但当氢原子置于强外电场中，并且研究的为低态激发态时，微扰法就不能给出有意义的结果.有时人们期望能够找到含时薛定谔方程的解析解(或半析解解).这是由于解析解(或半解析解)不仅给出的结果简单，便于把握规律，而且物理意义明确.但是，解析法或半解析法的结果仅仅对某些特定的原子或特定的条件才适用.因此，它的应用范围受到了很大的限制.事实上，比微扰法、解析法(或半解析法)应用范围广的方法是直接数求解法.随着计算机性能和速度的飞速提高和计算方法的不断完善，使用计算机来直接进行数值求解就显得更加容易了.针对微扰法和解析法(或半解析法)的不足，我们采用了数值对角化来研究氢原Stark位移.1979年，Zimmerman 等[5]利用对角化的办法研究了里德堡碱金属原子的Stark效应，并且得到与实验符合的结果.

本文首先给出氢原子在外电场中的哈密顿算符，并写出与其对应的矩阵表达式，然后通过零场下氢原子的本征值和本征函数来构造静电场中的波函数，再通过数值对角化方法得到任意态氢原子的Stark位移.

1 理论方法

外电场中，不考虑电子的自旋和相对论效应，氢原子的哈密顿算符为(原子单位)

(1)

(2)

(3)

由于价电子所受的作用势为中心势，因此，零场下氢原子的波函数为

(4)

其中，Rn l(r)为径向波函数;Yl m(θ,φ)为球谐波函数;n,l,m分别为主量子数、角量子数和磁量子数.

(5)

当存在外电场时，本征值方程为[6]

(6)

(7)

用Φi左乘(6)式并积分得到

(8)

其中，哈密顿矩阵元为

(9)

(10)

(11)

理想情况下，(7)式中的求和应该取无穷多项，但在实际计算中很难实现.如何选择求和的基函数，对实际的计算具有重要意义.求和中参与求和的基函数及相应的个数选择得当，不仅可以大大减少计算工作量，而且还可以保证必要的精度.

在一般情形下，只有能量在所研究的态邻近的那些激发态会对所研究的态产生较大影响.因此可以选择其附近能区内的态函数作为基函数.用(n,l)表示绝热近似下与自由原子主量子数为n,角量子数为l相联系的Stark态，而用(n,li-lj)表示(n,l),(n,li+1),…(n,lj)等一组相邻近的Stark态.

2 结果与讨论

2.1 基函数的选取

在氢原子9S态对应能量处，上下对称的截取n=6到n=11的态作为基函数组，得到的51个自由原子的波函数，为了检验基函数选取的完备性，同时选取主量子数n=1到n=15所有120个自由原子波函数作为基函数组.最后得到的两组结果符合的很好，相差最多不超过10-6Hartree.表1为计算得到的结果.

可见，在选取基函数时，只要选取的基保证有足够的精度就行.这样，即减少了对计算机内存需求，又提高了计算效率.

表1 Stark态9S能量随静电场强度的变化(0.01 Hartree)

2.2 氢原子的Stark位移

下面根据基函数的选取，所研究的态邻近的那些激发态会对所研究的态产生较大影响，选择其附近能区内的态函数作为基函数.通过数值对角化的办法，研究氢原子在不同外电场强度下，不同主量子数的Stark位移结果.

2.2.1 氢原子置于外电场中n=7附近的一簇Stark位移 在计算时，截取n=4到n=10，则基函数组由自由原子的波函数(4，0-3)，(5，0-4)，(6，0-5)，(7，0-6)，(8，0-7)，(9，0-8)，(10，0-9)组成，共记49个，得到图1.从图1可以看出，氢原子n相同l不同的态，在零场下是简并的，置于外电场中发生了Stark分裂.在一定的外电场范围内电场强度与能量呈线性关系.从这些Stark态中可以看出它们的间距大致相等，并且可以计算n相同l不同的两个Stark态的大致能量之差，得到它们的差值大致相等.

图1 氢原子附近的一簇Stark态

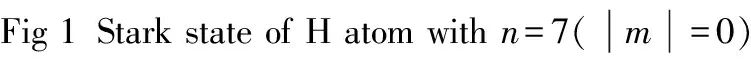
2.2.2 氢原子在外电场中n=7和n=10附近的两簇Stark位移的比较 在计算时，分别截取n=4到n=10和n=7到n=13作为基函数组，分别得到49个自由原子的波函数和70个自由原子的波函数，如图2所示.从图中可以看出，两簇Stark能谱中，n相同l不同的两个Stark态，n越大的发生Stark位移越大，n越小的发生的Stark位移越小.

图2 氢原子n=7和附近两簇的Stark位移

2.2.3 氢原子在外电场中n=15和n=16相邻的两簇Stark位移比较 在计算时，截取n=13到n=18，则基函数由自由原子的波函数(13，0-12)，(14，0-13)，(15，0-14)，(16，0-15)，(17，0-16)，(18，0-17)组成，共记93个，得到Stark态(15，14)和Stark态(16，0)相交，如图3所示.可以看出,两组邻近的能态发生Stark分裂时，在某一外电场范围内Stark态(n,n-1)与Stark态(n+1,0)会发生交叉，如图3中A点.该点所对应的外电场强度大致为2 070 V·cm-1.

为了更好地检验基函数选取的有效性以及更深入地研究Stark效应，下面来研究较高激发态的氢原子.

图3 氢原子n=15和附近两簇的Stark位移Fig 3 Stark state of H atom with n=15

2.2.4 氢原子在外电场中n=17和n=18相邻的两簇Stark位移 计算时，分别截取n=15到n=20，则基函数组由自由原子的波函数由(15，0-14)，(16，0-15)，(17，0-16)，(18，0-15)，(19，0-18)，(19，0-18)，(20，0-19)组成，共记124个，得到Stark态(17，16)和Stark态(18，0)发生交叉，如图4中A点，并且A点对应的外电场强度大致为1 260 V·cm-1.

由图3和图4比较可以看出,它们交叉点的位置不同.并可以明显地看出图4中A点所对应的外电场强度比图3中A点所对应的外电场强度小.

图4 氢原子n=17和附近两簇的Stark位移Fig 4 Stark state of H atom with n=17

综上所述，氢原子置于外电场中发生Stark分裂时，在一定的外电场范围内电场强度与能量呈线性关系，并且相邻的两Stark态之间的间距大致相等.在两簇相邻的Stark能谱中，在外电场强度足够的条件下，Stark态(n,n-1)和Stark态(n+1,0)会在某一定外电场范围内会发生第交叉，且该交叉点所对应的外电场强度随主量子数n的升高而降低.

3 结束语

针对微扰法、解析法(或半解析法)的不足，采用数值对角化的办法研究了氢原子置于外电场时的Stark位移.研究表明，用数值对角化的方法无论研究弱场还是强场下的高、低激发态的氢原子的Stark位移，都能得到很好的结果.另外，本文还给出了不同主量子数下Stark态的分裂规律，比较了Stark态能级交叉点随n的变化情况.

[1] 时庆云.量子力学[M].北京：北京理工大学出版社，1993：256-259.

[2] 曾谨言.量子力学：卷Ⅰ[M].北京：科学出版社,2001：356-347

[3] 许新胜，张先燚,涂兴华.氢原子低能级的Stark效应[J].安徽师范大学学报：自然科学版,2001，24(1):21-26.

[4] 苏燕飞，张昌莘,席伟.氢原子Stark效应的能级分裂规律[J].大学物理,2004,24(2):8-10.

[5] ZIMMERMAN M L,LITTMAN M G,KASH M M,et al.Stark structure of the Rydberg states of alkali-metal atoms[J].PhysRevA 1979,20(6):2251-2275.

[6] 张现周.频率调制场中里德堡原子的激发与态囚禁[D].武汉：中国科学院武汉物理与数学研究所，2003.

[7] HOOKER A,GREENE C H,WILUAM C.Classical examination of the Stark effect in hydrogen[J].PhysRevA 1997,55(6):4069-4612.

(责任编辑 孙对兄)

Theoretical study on level energy shift of H atom

FAN Juan,LI Xiao-yong,WANG Wen-hai

(Experimental Center,Northwest University for Nationalities,Lanzhou 730030,Gansu,China)

By using the numerical diagonalization method,Stark effect of hydrogen atoms has been studied by solving Schrödinger equation for hydrogen atoms in the static field,then we obtain the Stark shifts of the states which are in the neighborhood ofn=7,10,15,16,17,18.

Stark shift;hydrogen atom;diagonalization

2014-12-05;修改稿收到日期:2015-03-20

国家民委科研基金资助项目(14XB2019)；西北民族大学中青年基金资助项目(N12098,x2010-6)；西北民族大学大学生创新基金资助项目

樊娟(1984—)，女，甘肃渭源人，实验师.主要研究方向为非线性光学、物理教育. E-mail:fanjuan@xbmu.edu.cn*通讯联系人，男，甘肃宁县人，高级实验师，博士.主要研究方向为强激光场中的原子物理.E-mail:lxycock@163.com

O 562.3+2

A

1001-988Ⅹ(2015)04-0034-04