“数形结合”巧解小学数学中时间的计算

贵州省凯里市丹寨县南皋小学 王玉祥

顾名思义，“数形结合”就是数据和图形相结合。利用“数形结合”解题的方法，在学生各学段都应用广泛，因为使用数形结合解题，解题思路比较清晰、明了。在这里，笔者就以本人所执教的三年级人教版数学上册——时间的计算为例来浅谈“数形结合”的应用。

笔者所执教的三年级是从一年级开始带班的，所以对本班学情还是有所了解。由于笔者本人执教资历尚浅，没意识到数形结合对解题的重要性，所以在之前的教学中，若是单元不做要求的，笔者都很少结合图形去解题，只是要求学生多读题后解决问题。所以学生对数形结合解题的认知能力也较差。

当上完《时间的计算》时，学生头痛了，不会做题；笔者本人也很是头痛，到底用什么方法去引导学生呢？不管如何，学生不懂的太多，复习课是必须上的了。复习课所用的例题如下。

例、偿卡走到南皋小学需要15分钟。（南皋小学是偿卡村生源就读的小学）

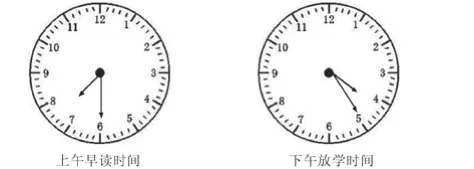
（1）潘冬梅同学早上最迟多少时间出发，上学才不迟到? （潘冬梅系笔者班级偿卡籍学生）

（2）如果潘冬梅因为打扫卫生，下午放学回到家后已经5：10，潘冬梅打扫卫生用了多长时间？

按照解题惯例，是要先读出钟面的时间。学生也确实能读出钟面的时间：

上午早读时间：7：30

下午放学时间：4：25

通常解决问题的方式是：

解：（1）分析，找出知道的信息：

①7：30早读；

②由偿卡走到南皋小学需要15分钟。

需要解决的问题：

最迟多少时间出发上学才不迟到？——不迟到就是在7：30之前到学校才不迟到。

多少时间出发？不知道，但是经过15分钟后就是7：30，列式：

+15分钟=7：30 即：

7：30－15分钟=7：15

答：最迟7：15出发上学才不迟到。

（2）分析，找出知道的信息：

①4：25放学；

②南皋小学到偿卡需要15分钟；

③5：10到家。

需要解决的问题：

打扫卫生用的时间是多长？

（打扫卫生用的时长）+（从学校走到家需要的时长）=（回到家的时间）－（学校放学的时间）

即：

5：10－4：25=45分钟

打扫卫生用的时长=（4 5分钟）－（从学校走到家的时长）

即：

45分钟－15分钟=30分钟

答：打扫卫生用的时间是30分钟。

对于第（1）题，笔者大部分学生还是可以解决的，但是对于第（2）题，笔者的绝大部分学生就只能等待答案了。笔者苦思一晚，只有借助线段图来解决问题了。

那么，在解决时间计算时如何巧用“数形结合”呢？

还是引用这个例题：

学生已经读出钟面的时间：

上午早读时间：7：30

下午放学时间：4：25

（1）由已经知道的信息作图：

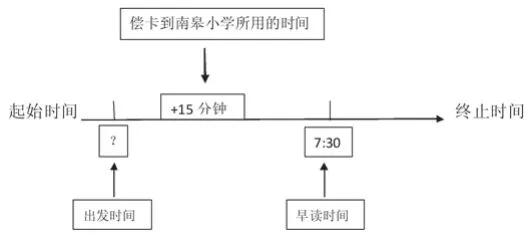
运用一年级学过的知识，学生很快求出，列式：

7：30－15分钟=7：15

答：最迟7：15出发上学才不迟到。

（2）由已经知道的信息作图：

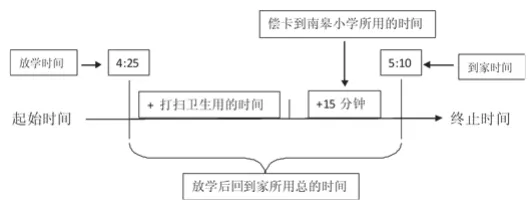
当然，线段图还可以简化为：

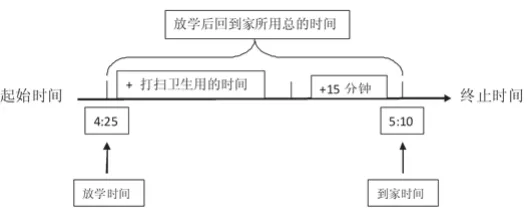
同样，运用一年级线段图的知识，学生就可以列式：

5：10－4：25=45分钟

45分钟－15分钟=30分钟

答：打扫卫生用的时间是30分钟。

通过运用“数形结合”解题，感觉学生的学习热情高涨了许多，学生对时间的计算能力也有所增强。毕竟，有研究表明，人对视频的理解能力较强，其次到图，对文字的理解能力则再次之。

总之，教师注重对学生“数形结合”能力的培养，不仅教师教得轻松，学生也会学得轻松。