台后填土与主梁的相互作用对梁桥纵向地震反应的影响
2015-06-28李建中
王 翼 李建中
(1.同济大学桥梁工程系,上海200092;2.安徽工业大学建工学院,马鞍山243032)
1 引言
由于我国西部地区以高原、山地、盆地为主,地形、地貌以及地质条件较为复杂,中小跨度梁桥在线路中往往占很大比例[1]。在这些桥梁在纵桥向往往只单独依靠桥墩抵抗地震作用,这就需要将桥墩的截面尺寸加大或是增加配筋,从而降低全桥的经济性。在1971年的San Fernando地震后,很多桥梁结构发现动力行为受到桥台的约束作用影响显著,尤其是对于短跨刚度大的桥梁的影响更为明显。汶川地震也显示桥台可以约束桥跨结构的位移,甚至对于上部结构的落梁有显著影响,如高原大桥因一侧桥台被桥跨结构撞坏并被顶入路堤50 cm以上,致使第三跨纵向位移过大而落梁[2],而寿江大桥同样发生纵向大位移,尽管桥台被破坏,但因背墙和台后填土的阻挡而避免落梁[3]。这证明桥台台后填土确实承受较大的地震作用,并在地震时能有效减少对桥梁产生的作用。
在我国现行规范中,由于当时的技术科研水平,《公路桥梁抗震设计细则》[4]对桥台在地震中的作用没有任何规定。在设计计算时或者仅考虑桥墩对主梁的纵向约束,或者认为桥台与主梁刚接。
AASHTO桥梁抗震设计规范[5]在关于桥台中规定:设计者可以选择是否将桥台作为抗震体系的一部分。当桥台不作为抗震体系的一部分时,抗震的目标是中间墩柱承担全部上部结构的地震惯性力,桥台需设置足够的搭接长度,确保能够满足上部结构与桥台之间的相对位移。当桥台作为地震抗震体系中的一部分时,抗震设计目标是利用桥台的刚度和能力约束主梁的地震位移,帮助桥墩柱传递主梁的地震惯性力。但在地震作用下桥台往往因承受过大地震力而使得桥台基础被破坏。所以在桥梁纵向,CALTRANS[6]桥梁抗震设计标准建议背墙在地震下可以被剪断,并利用“背墙-填土”体系的刚度和能力传递部分地震惯性力,如图1所示,以保护基础受到地震损伤。而桥梁的纵向地震惯性力主要依靠台后填土来承受。
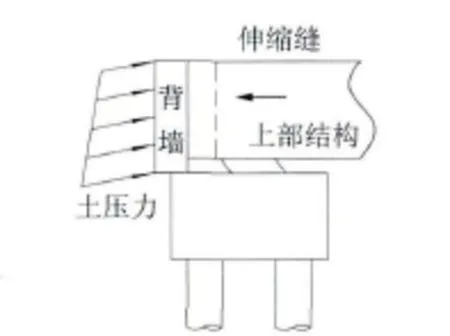
图1 背墙-填土体系Fig.1 System of“Backwall-backfill”
目前对于这种台后土与主梁相互作用的文献较少。本文假设桥台背墙在地震作用下是被破坏的构件,考虑台后土对主梁的非线性约束建立了主梁-台后土相互作用有限元模型,采用非线性时程方法分析了桥台与主梁之间的间隙比、填土类型对桥梁纵向地震响应的影响。
2 工程背景及地震动输入
2.1 工程背景
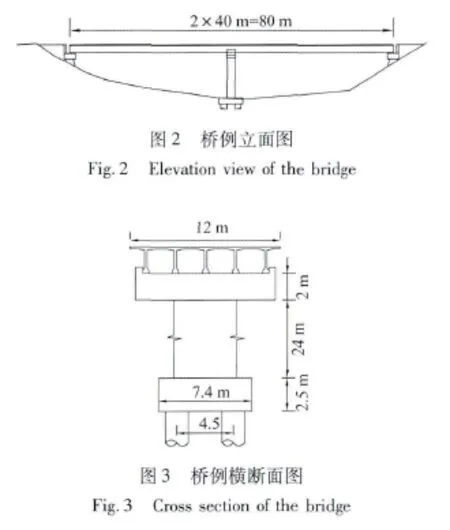
本文以典型的两跨刚构桥为工程背景,如图2、图3所示。全桥跨径布置为2×40 m,主梁为材料C50混凝土的T梁,梁宽12 m,梁高为2 m;桥墩材料为C40混凝土,采用5 m×2 m的矩形桥墩,墩高为24 m。主梁纵向两侧为典型的座式桥台,桥台背墙高度为2 m。桥墩与主梁固结,两侧桥台处采用四氟滑板支座。
2.2 地震动输入
按照9度抗震设防烈度,二类场地生成水平设计加速度设计谱。根据《公路桥梁抗震设计细则》第6.4.2条,采用7组及以上地震加速度时程计算时,可取结果的平均值。按照设计加速度反应谱,采用的7组地震加速度时程来自太平洋地震工程中心的地震波数据库(PEER Strong Motion Database)。为使地震波作用更接近设计谱的作用,对其进行调幅,将加速度峰值调整为0.688 5 g,如表1所示。图4显示了经过调幅后7条地震波所对应的加速度反应谱。
2.3 分析工况
为了研究台后土对于桥梁地震反应的影响,本文对以下3种工况建立了动力模型,并采用非线性时程法对结构进行地震反应分析。
工况一:不将桥台作为抗震体系的一部分,同时忽略台后填土与主梁之间的相互作用,只考虑桥墩对桥梁纵向反应的影响,记为工况C-free。
工况二:假设桥台背墙在地震中被剪断,考虑主梁与台后土的相互作用,研究背墙与主梁之间间隙大小对桥梁纵向地震反应的影响。为了更好地分析伸缩缝间隙对于桥梁抗震的影响,对台后背墙与主梁之间的间隙进行标准化参数分析,即以工况一为基准,获得的梁端位移作为最大间隙Δmax,伸缩缝初始间隙为ΔG,引入无量纲参数——间隙比rG,
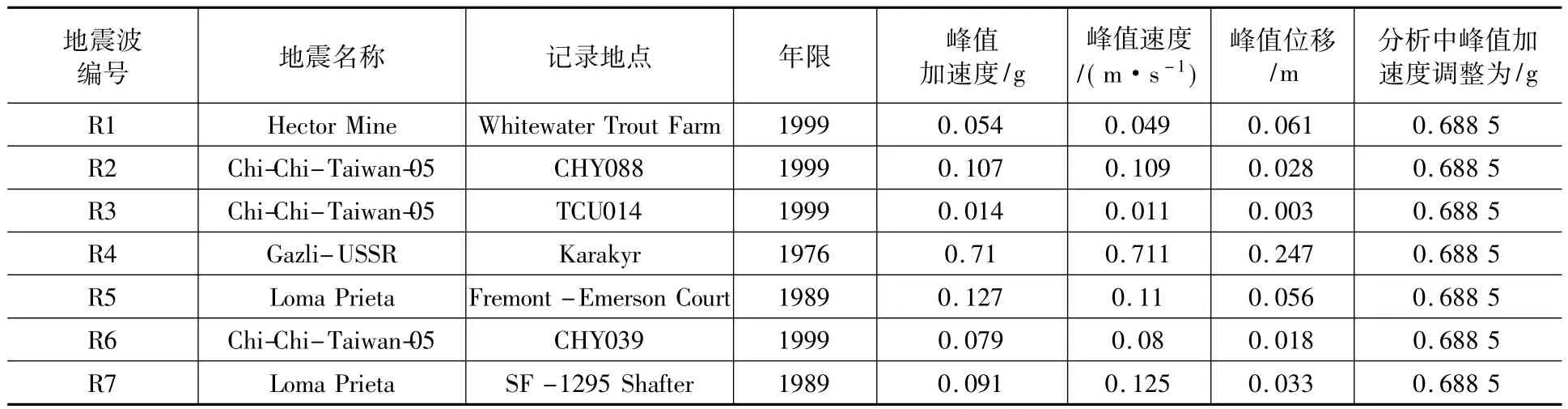
表1 地震动输入Table 1 Earthquake input

当初始间隙ΔG取值为Δmax时,即rG=1时,主梁与桥台背墙没有接触,只考虑桥墩对桥梁纵向地震反应的影响,即为工况一;当初始间隙ΔG取值为0时,即rG=0时桥台背墙与主梁间间隙为0。在间隙比rG在0~1之间时,考虑台后土对主梁的纵向的非线性约束。
工况三:假设桥台背墙在地震中被剪断,考虑主梁与台后土的相互作用,研究台后土性质对于桥梁纵向地震反应的影响。根据填土类型为黏性土工况和非黏性土工况分别记为C-N和C-FN。
3 台后土-主梁相互作用动力分析模型
3.1 台后填土的模拟
经典的被动土压力理论,诸如库仑理论、朗肯理论和对数螺旋线方法给出的是“墙-土”体系的最大被动土压力,不能给出墙被推向填土的过程中“墙-土”体系的力-位移关系,因此这些理论可以用来确定“墙-土”体系的最大被动抵抗能力,但在地震作用下无法反映墙体的位移与土压力的关系,从而也无法得到台后填土对于桥梁的影响。鉴于此,Duncan和Mokwa[7]提出采用双曲线函数来表示被动土压力与墙体位移之间的关系,即
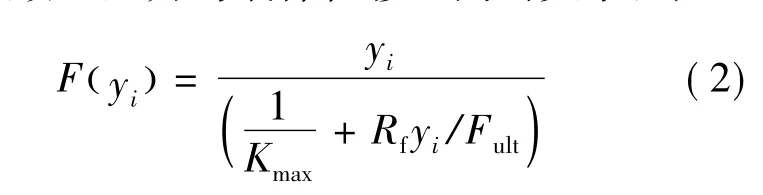
式中,F为被动土压力;Fult为最大被动土压力;yi为土的变形;Rf为最大被动土压力与双曲线的渐近线的比值;Kmax为土的力位移曲线的初始切线刚度。
这种关系如图4所示。
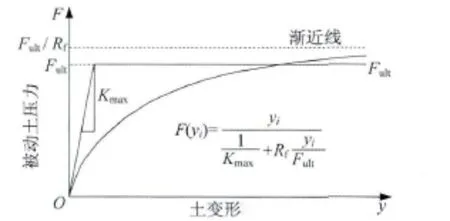
图4 力位移关系双曲线模型Fig.4 Hyperbolic model of the stress-strain relationship
3.2 全桥动力分析模型
采用OpenSees程序来建立桥梁的空间动力有限元模型。主梁采用线弹性梁单元模拟,每跨划分成8个等长单元以使主梁质量分布更趋合理。仅考虑桥台处支座对主梁的支承,忽略支座的摩擦效应对主梁的影响。墩柱采用三维弹塑性纤维单元模拟,其中混凝土采用Kent-Scott-Park本构模型,约束混凝土的抗压强度、极限应变等参数根据Mander公式[8]确定;钢筋则采用简化的理想弹塑性双线性本构模型。背墙与主梁之间设置伸缩缝,当在地震作用下主梁与背墙接触时,背墙会被剪断,忽略背墙的滞回耗能效应,完全由台后填土承受纵向地震惯性力。Shamsabadi基于大量足尺试验结果和经验,给出在没有地质数据时可以采用两种刚度不同而最大被动土压力相同的粘土和非粘性土数据。台后填土参数根据Shamsabadi[9]转换结果见表 2。
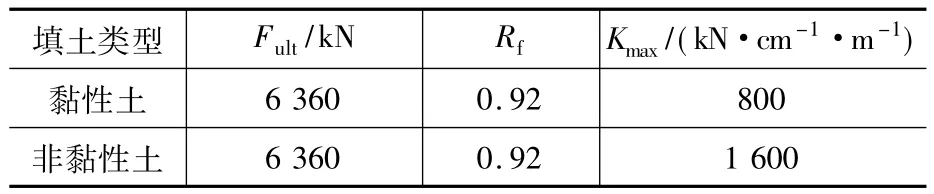
表2 台后填土参数Table 2 Parameters for abutment backfills
桩基础引入集中土弹簧加以模拟。模型简图如图5所示。
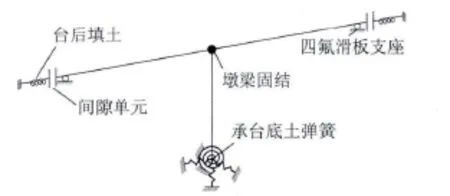
图5 动力分析中的梁桥模型Fig.5 Girder bridge model in dynamic analysis
4 台后土与主梁相互作用结果分析
本文研究参量为桥梁在地震作用下的桥墩最大曲率、主梁纵向最大位移、桥墩残余曲率及主梁纵向残余位移。为了更好地分析桥梁在地震作用下的反应,消除量纲影响,本文将以工况一下的桥梁地震反应结果为基准将所有工况下的地震反应进行归一化处理。
图6-图9分别为以间隙比为变量,桥墩的最大曲率、主梁纵向最大位移、桥墩残余曲率及主梁纵向残余位移的变化图。
从图6、图7中可以看到,在间隙比在0.4~1范围时,桥墩的曲率与主梁纵向最大位移随着间隙比的增加而线性增长;在间隙比为0~0.4范围时桥墩的曲率与主梁纵向最大位移变化较为复杂。以采用非黏性填土在R7波作用下为例,在间隙比从0~0.1范围变化时,主梁的纵向最大位移随间隙比增大从原先的12.4 cm增加到13.2 cm(图10(a)、图 10(b)),增幅只有 0.8 cm。从图10(a)可以看到,因为在间隙比为0时,台后填土在地震作用下较早进入屈服阶段,刚度接近于0,对主梁的控制效果反而不如间隙比为0.1时的效果。当间隙比从0.1增加到0.3时,因为台后土的屈服程度没有明显变化,主梁的最大位移从13.2 cm 增大到 18.3 cm(图 10(b)、图 10(c))。在间隙比从0.3到0.4过渡时,因为间隙比为0.4时台后填土进入屈服程度较低,还具有一定的刚度,可以控制主梁的纵向位移,使得最大位移从18.3 cm 仅增到 19.8 cm(图 10(c)、图 10(d)),桥墩曲率的增长幅度也较小(图6)。当间隙比进一步增加时,虽然填土进入屈服程度更小,但因为间隙比较大,主梁受到填土作用影响之前已发生较大位移而无法对于桥墩的曲率产生较大影响(图6)。从图10可看出,因为间隙比的变化对于台后填土的屈服程度影响较大,而从台后填土从屈服到弹性受力的这一过程对于桥墩曲率和主梁位移影响非常明显,所以桥台背墙与主梁之间的间隙取值非常重要。根据桥墩的曲率、主梁纵向位移与间隙比的关系图(图6、图7),当间隙比取值应小于0.4时,可以有效地减小主梁纵向位移和桥墩曲率。
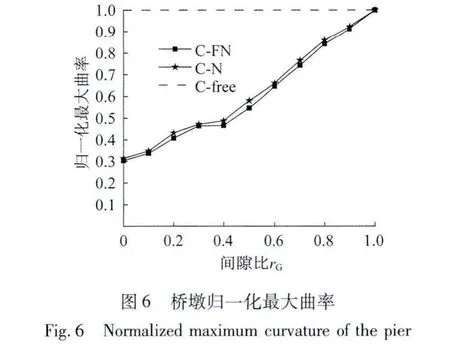
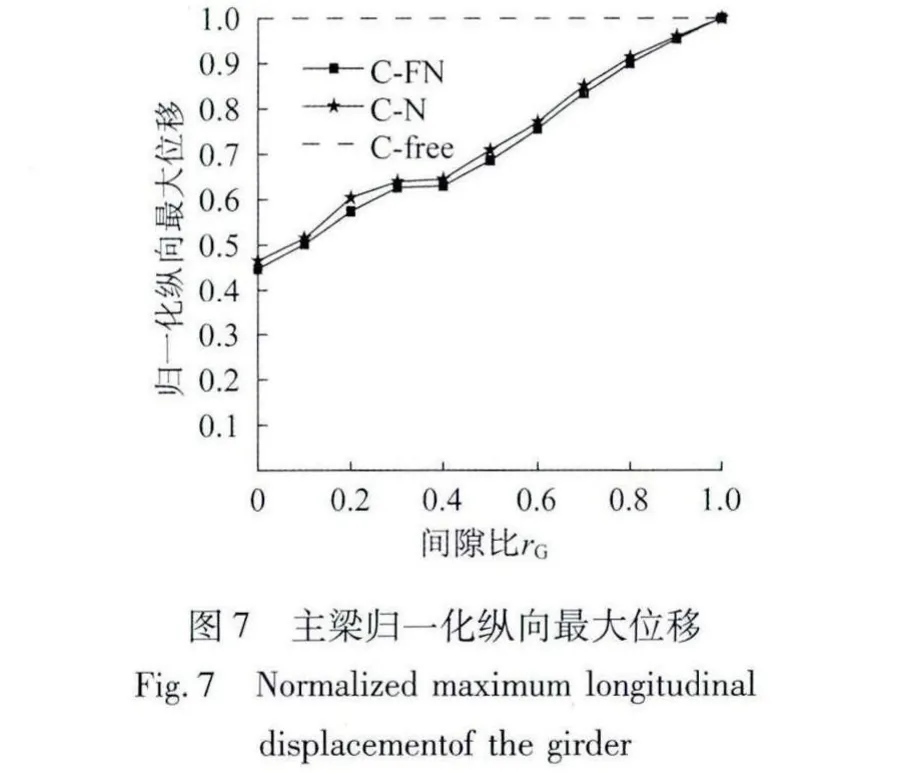
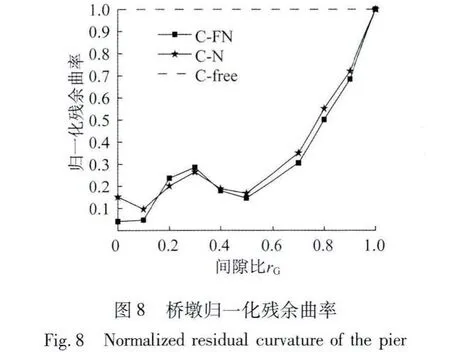
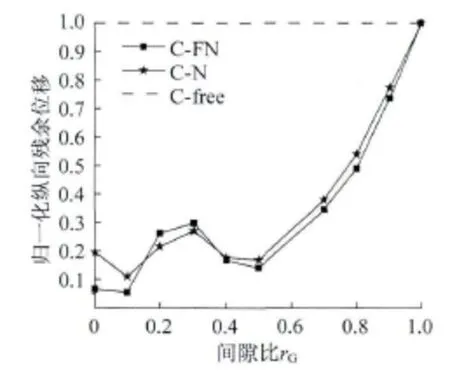
图9 主梁归一化纵向残余位移Fig.9 Normalized residual longitudinal displacement of the girder
当仅考虑桥墩对主梁的纵向约束作用时,与间隙比大于0.7的真实情况相比,针对于采用非黏性填土和黏性填土的工况标准化曲率误差分别为26%和23%,标准化主梁位移误差分别为17%和15%,即当间隙比小于0.7时,仅考虑桥墩对主梁的纵向约束作用无法反映真实情况。
假设某强震区按两水准抗震设计,并要求在第一水准保持弹性。出现这种情况如果按照仅考虑桥墩对主梁纵向约束作用的影响,会导致设计过于保守。因为这时可能会错误判断墩柱的状态(实际墩柱保持弹性,而忽略纵向约束作用则会认为桥墩状态相反),从而加强桥墩配筋,改变了全桥基频,造成能力保护构件需求增加,大大降低了结构的经济性。
从图8、图9中可以看到当间隙比从0增加到0.1时,桥墩的标准化残余曲率与主梁的标准化纵向残余位移都有不同程度的减小,这是因为在间隙比为0时,台后填土过早屈服,其刚度较间隙比为0.1时的台后土低,对于主梁后期的位移控制能力较弱(图10(a)、图10(b))。间隙比在0.1~0.3范围内,主梁的最大位移随着间隙比的增大而增加,而台后土的屈服程度相近,使得主梁的纵向残余位移及桥墩残余曲率也随着间隙比的增大而增长(图10(b)、图10(c))。间隙比在0.3增长到0.4~0.5时,桥台后填土进入屈服程度减小,具有较大刚度,能提供较大的回复力控制主梁后期的纵向位移,使得桥墩的残余曲率与主梁位移都随着间隙比的增大而减小(图10(c)、图10(d))。
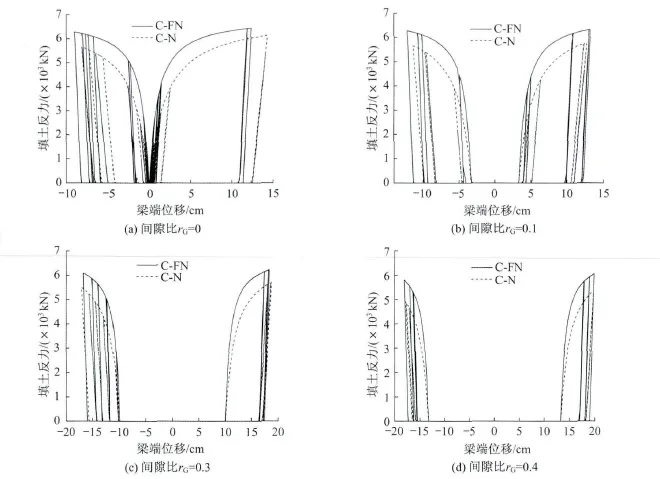
图10 R7波作用下的桥台背墙的力位移曲线Fig.10 Force-displacement curves of the abutment backwall due to the R7 input motion
当间隙比位于0.5~1时,虽然台后填土体没有屈服,刚度较大,但因为间隙比太大,无法对主梁提供足够的回复力,使得桥墩残余曲率和主梁残余位移随着间隙比增大而增大。同时从图8、图9可以看到仅当间隙比在0.9以上时,主梁残余位移和桥墩残余曲率的真实值与忽略对主梁纵向约束的偏差才能小于30%,即当间隙比小于0.9时,忽略桥台与台后填土对于主梁的纵向约束作用无法反映主梁纵向残余位移与桥墩的残余曲率的真实情况。
5 结论与建议
本文通过数值模拟的办法讨论了桥台台后填土对采用墩梁固结的规则连续梁桥纵向地震反应及当前简化分析方法的影响,主要结论如下:
(1)仅考虑桥墩对桥梁纵向反应的影响会高估主梁的纵向位移以及墩底截面的曲率需求。这种简化方法的可靠性与间隙比大小密切相关。
(2)在桥梁抗震分析中,当间隙较小时,台后填土能较好地控制桥墩最大曲率和主梁最大位移,总体上随着间隙比的增大控制能力减弱。但在台后填土的屈服程度有明显变化的这一阶段,即便间隙比略有增大,主梁的位移和桥墩曲率没有明显变化。当间隙比大于0.4时,桥墩的最大曲率与主梁位移随着间隙比的增大而线性增长。建议桥台背墙与主梁之间间隙取到间隙比小于0.4以下的宽度。
(3)在桥梁抗震分析中,台后填土不仅在间隙比为0.1时对于桥墩的残余曲率和主梁的残余位移有较好的控制,当台后填土屈服程度有明显变化这一阶段时,桥墩残余曲率和主梁残余位移也能限制在较小的范围。
[1] 魏标.典型非规则梁桥抗震设计理论[D].上海:同济大学,2010.Wei Biao.Seismic design theory of irregular continuous bridges[D].Shanghai:Tongji University,2010.(in Chinese)
[2] 李鸿晶,陆鸣,温增平,等.汶川地震桥梁震害的特征[J].南京工业大学学报(自然科学版),2009,31(1):24-29.Li Hongjing,Lu Ming,Wen Zengping,et al.Characteristics of bridge damages in Wenchuan earthquake[J].Journal of Nanjing University of Technology(Natural Science Edition),2009,31(1):24-29.(in Chinese)
[3] 王东升,郭迅,孙治国,等.汶川大地震公路桥梁震害初步调查[J].地震工程与工程振动,2009,29(3):84-94.Wang Dongsheng,Guo Xun,Sun Zhiguo,et al.Damage to highway bridges during Wenchuan earthquake[J].Journal of Earthquake Engineering and Engineering Vibration,2009,29(3):84-94.(in Chinese)
[4] 中华人民共和国交通运输部.JTG/T B02-01—2008公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.Ministry of Transport of the People’s Republic of China.JTG/T B02—01—2008 Guidelines for seismic design of highway bridges[S].Beijing:China Communications Press,2008.(in Chinese)
[5] AASHTO.Guide specifications for LRFD seismic bridge design[S].American Association of State Highway and Transportation Officials:Washington,D.C.USA,2009.
[6] CALTRANS.Seismic design criteria[S].California:California Department of Transportation,2010.
[7] Michael Duncan J,Robert L,Mokwa.Passive earth pressures:theories and tests[J].Journal of Geotechnical and Geoenvironmental Engineering,2001,127(3):248-257.
[8] Shamsabadi A,Rollins K M,Kapuskar M.Nonlinear soil-abutment-bridge structure interaction for seismic performance-based design[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(6):707-720.
[9] Mander J B,Priestley M J N,Park R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,1989,114(8):1804-1826.
