低复杂度的连续相位调制与LDPC联合迭代译码算法*

张 凯

(西安烽火电子科技有限责任公司,西安710075)

低复杂度的连续相位调制与LDPC联合迭代译码算法*

张 凯**

(西安烽火电子科技有限责任公司,西安710075)

连续相位调制与低密度奇偶校验(LDPC)码编译码技术在提高频谱利用率的同时能够有效降低发射功率,然而这会增加通信系统的复杂度。为此,提出了一种低复杂度的联合迭代译码算法解决此问题。该算法以符号/比特的可靠度作为内外译码器之间的迭代信息。仿真结果表明,新的联合迭代译码算法的性能与概率域下的算法几乎没有差异,在总迭代次数相同的情况下,采用低复杂度联合迭代的性能相比于未采用联合迭代的性能有约0.75 dB的增益。

低密度奇偶校验码;连续相位调制;可靠度信息;联合迭代译码

1 引 言

随着无线通信技术的快速发展,日益增长的通信业务需求与频谱资源之间的矛盾逐渐显现。为了解决这一问题,通常采用连续相位调制(Continuous -Phase Modulation,CPM)技术。CPM信号具有较高的频谱效率、较低的带外功率、信号恒包络等特性[1],能够有效地克服频谱资源日益紧缺这一问题。低密度奇偶校验(Low-density Parity-check, LDPC)码最早由Gallager于1963年在他的博士论文中提出[2]。研究发现,当采用和-积译码算法[3](Sum-Product Algorithm,SPA)时,其译码性能与Turbo码相似[4-5]。将现代编译码技术与CPM调制技术相结合,不但能够提高系统的可靠性而且还能够提升频谱利用率,非常适用于带宽受限、可靠性要求较高的通信系统。然而,由于CPM软解调算法(BCJR算法)[6]与LDPC的SPA译码算法涉及了大量的指数、乘法和归一化运算,导致这类算法的复杂度非常高,不利于硬件实现。

针对如上问题,本文给出了通用的信息度量定义,简化了CPM软解调算法,降低了算法复杂度,进而提出了基于可靠度的低复杂度联合迭代译码算法。仿真结果表明,基于可靠度的低复杂度联合迭代译码算法的性能与概率域下的算法几乎没有差异。

2 CPM信号调制与解调

2.1 信号表达式

CPM信号归一化功率基带复包络数学表达式为

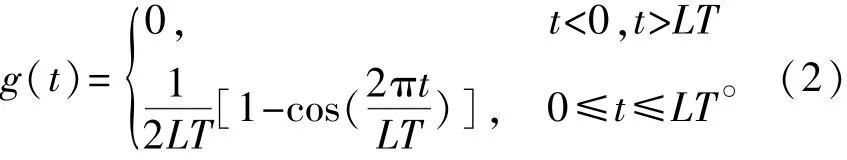
式中,L为正整数。当L=1时,CPM为全响应;当L≥1时,CPM为部分响应。φ(t,X)表示时变相位, h为调制指数,X={X0,X1,…,Xn,…XN-1}表示长度为N的信息序列,Xn(0≤n＜N)取值集合为{x|x= 2(i-M)+1,i=0,1,…,M-1},其中,M表示进制数。令B(x)=[b0,b1,…,blbM-1]为与符号x相对应的整数i的二进制序列。

2.2 CPM调制与解调

为了简单起见,本文仅考虑L=1时的CPM信号。从编码的角度来看,可以将CPM的调制过程看作是在Trellis[7]上的编码过程。图1给出了调制指数2CPM/h=0.5时的Trellis。

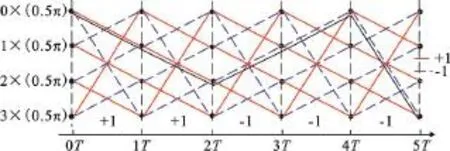
图1 2CPM/h=0.5时的TrellisFig.1 Trellis of 2CPM with h=0.5

对于任意给定的信息序列,Trellis上都有一条与之对应的路径,路径反映了CPM信号相位变化的情况。假设输入信息X=(+1,+1,-1,-1,-1),初始相位为0,则每个CPM符号结束时相位状态依次为。CPM信号起始(或终止)相位状态集合为S={0,πh,2πh,…,种取值,为方便表示,将其简记为S={0,1,2,条边,记为,上标x表示输入的符号,下标p、q表示从相位状态p变化至q。每条边对应一段CPM波形(t),因此Trellis上的边调制波形(t)存在对应关系。完整的CPM信号就是由各段(t)拼接得到的。

基于概率域下的CPM软解调算法描述详见文献[8],由于篇幅所限,这里不再赘述。

3 低复杂度软解调算法

3.1 信号模型

设每段CPM波形采样K点,第n个符号对应的调制信号波形为sn(t),经高斯信道后,接收端采样值为

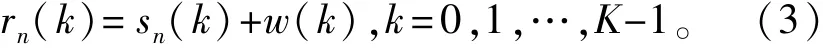
式中,sn(k)为sn(t)的采样值,w(k)为服从均值为0、方差为σ2的二维高斯分布的采样值。第n(0≤n＜N)节Trellis各条边的后验概率γn(p,q)计算如下:

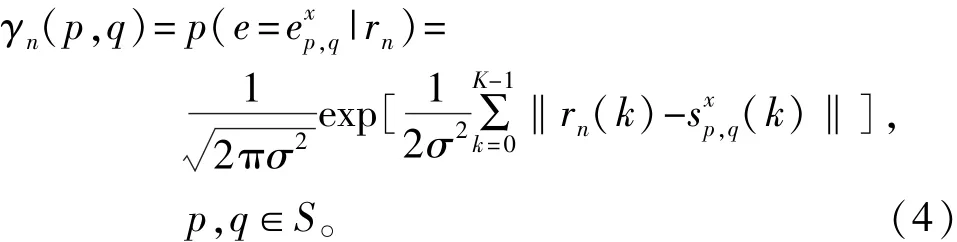
式中,符号‖·‖表示欧氏距离。

3.2 信息度量的定义

低复杂度软解调算法以概率的对数作为信息度量。对式(4)求对数得

式中,I[x]、Q[x]分别表示x的实部和虚部。在一个符号周期T内,上式第一项和第二项都是与(或(t))独立的。考虑到对数域信息度量R[γn(p,q)]一般具有如下形式:R(γ)=a0ln(γ)+ a1,其中,a0a1是两个与γ独立的参数。那么,对于上式,通过选择合适的a0、a1并进行线性变换后,可得到边的可靠度信息

上式说明,可靠度Rn(可以看作接收信号和发送调制信号之间的一种“相关操作”,这种相关操作有可能会过高估计某些“可靠”的信息分量,所以类似于文献[9],我们需要用修正系数ξ来降低这些过量的估计。修正后边的可靠度信息有如下形式:

3.3 可靠度平移准则

可靠度Rn()的数值在信息处理的过程中不断累加,可能会出现数值溢出的情况,为此我们给出可靠度向量Rn(V)的平移准则,f(Rn(V))=Rn(V)-max(Rn(V)),符号max(X)表示向量X中的最大数值。这样,经平移后最大的可靠度为0。

3.4 基于可靠度的软解调算法

算法1 基于可靠度的软解调算法

(1)初始化:根据式(6)和式(7)计算第n(0≤n＜N)节Trellis各条边修正后的可靠度信息Rn();

(2)前向递归:将前向递归变量初始化为α0= (0,-∞,…,-∞),递归计算

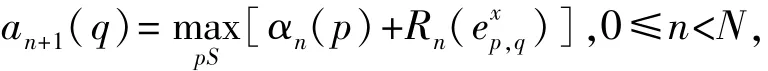
同时根据可靠度平移准则对信息向量αn+1进行平移;

(3)后向递归:将后向递归变量初始化为βn= (0,0,…,0),递归计算

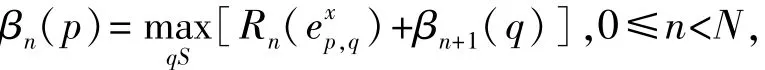
同时根据可靠度平移准则对信息向量βn进行平移;

(4)信息提取:关于第n个符号x的可靠度信息Rn(x)计算如下:

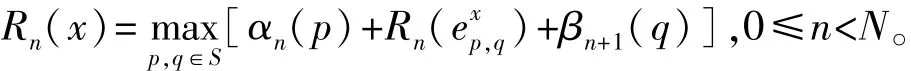
4 低复杂度的联合迭代译码

4.1 系统框图与信息迭代机制

联合迭代译码框图如图2所示,其过程是内译码器与外译码器相互传递信息、迭代的过程。首先,内译码器收到采样值和外译码器两者共同提供的信息进行译码,信号采样值提供的信息称为固有信息(Intrinsic Information),外译码器提供的信息称为先验信息(Prior Information),内译码器输出的是关于符号的可靠度信息,需要进行符号/比特信息转换。需要指出的是,在内外译码器的相互迭代过程中,需要去除外译码器传递给内译码器的信息,得到的差称为外信息(Extrinsic Information)。其次,外译码器将内译码器输出的外信息作为自身的先验信息进行译码,外译码器输出的是关于比特的可靠度信息,需要进行比特/符号信息转换。外译码器输出的信息需要去除内译码器传递给外译码器的先验信息。

图2 CPM联合迭代译码框图Fig.2 Block diagram of joint iterative decoding for CPM

这里需要指出的是,在迭代初始时刻外译码器的输入与输出的比特可靠度信息均为0。

4.2 符号-比特可靠度转换

比特-符号转换:符号x对应的二进制序列为B(x)=[b0,b1,…,blbM-1],则符号x的可靠度为

符号-比特转换:第n(0≤n＜N)个符号中第j(0≤j＜lbM)比特的可靠度计算如下:

4.3 低复杂度联合迭代译码算法

为了清楚直观地对低复杂度联合迭代译码算法进行描述,用带有下划线的符号表示从外译码器向内译码器方向传递的信息;带有上划线的符号表示由内译码器向外译码器方向传递的信息,上标表示迭代次数;(x)为第l次迭代时内译码器输出的第n个符号为x的可靠度;(j)为第l次迭代时符号-比特转换单元输出的第n个符号中第j比特的可靠度(j)为第l次迭代时输入外译码器的第n个符号中第j比特的可靠度;(j)为第l次迭代时外译码器输出的第n个符号中第j比特的可靠度;(j)为第l次迭代时输入比特-符号转换单元的第n个符号中第j比特的可靠度;(x)为第l次迭代时输入内译码器的第n个符号为x的可靠度;J为内译码器与外译码器之间的最大迭代次数。

算法2 低复杂度的联合迭代译码算法

(1)初始化:根据式(6)计算第n(0≤n＜N)节Trellis各条边的可靠度信息(,设置(j) =0,j)=0(0≤n＜N,0≤j＜lbM-1),内外译码器之间的迭代次数l=0;

(2)迭代:当l＜J时,执行以下步骤:

其中ξ为边可靠度信息的修正因子;

步骤4 内译码器译码:基于更新后的边可靠度,进行前向、后向递归并提取符号可靠度(x);

5 性能仿真结果

仿真所使用的LDPC码为随机构造[10],码率0.5,码长10 000,译码算法采用文献[11]中的量化最小和算法。

针对算法1考察基于可靠度的软解调算法性能。信道为高斯信道,调制方式选取2CPM/h=0.5、4CPM/h=0.25和8CPM/h=0.125,边的修正因子根据经验值设置为0.70,仿真结果如图3所示。为了便于比较,图中同时给出了概率域CPM解调算法下的性能曲线。从图中可以看到,不论CPM调制参数如何选取,基于概率域的解调算法和基于可靠度的解调算法的性能曲线完全一致。

图3 不同参数无LDPC码时的性能Fig.3 Error performances without LDPC

为了进一步考察LDPC码在CPM调制通信系统在高斯信道下的性能,我们对其进行了仿真,调制方式为4CPM/h=0.25,边的修正因子和译码器的修正因子根据经验值分别设置为0.7和0.8,迭代次数设置为30次,仿真结果如图4所示。为了便于比较,图中同时给出了CPM采用概率域下解调、译码采用SPA译码算法下的性能曲线。从曲线中可以看到在适当选取修正因子的情况下,两种算法的性能基本相同。例如在误码率BER=10-5时,两种算法间的差异仅有0.02 dB。

图4 4CPM/h=0.25有LDPC码时的性能Fig.4 4CPM/h=0.25 error performances with LDPC

针对算法2考察联合迭代译码算法的性能。信道为高斯信道,调制方式选取4CPM/h=0.25,边的修正因子和译码器的修正因子根据经验值分别设置为0.7和0.8。我们在两种不同参数下进行仿真,分别是Jglobal=1、Jlocal=30和Jglobal=3、Jlocal=10。对于不同参数下的译码复杂度,我们将从统计平均意义上进行衡量。统计每一帧完成译码后(不管成功与否)所需的本地迭代次数总和,然后对帧数进行平均,由此得到每一帧译码所需的平均本地迭代次数仿真结果如图5和图6所示。

图5 联合迭代译码性能曲线Fig.5 Error performances of joint iterative decoding algorithm

图6 联合迭代译码平均迭代次数Fig.6 Average number of iterations of joint iterative decoding algorithm

从图中可以看到:

(1)采用联合迭代译码后的性能明显优于未采用联合迭代译码的性能。例如,在误码率BER= 10-5时,采用联合迭代译码能够获得约0.75 dB的性能增益;

值得指出的是,解调器与译码器之间传递的信息均以可靠度作为度量,不需要对信道的噪声方差进行估计,避免了对噪声方差估计不准确而带来性能上的损失,同时简化了通信系统的结构。

6 结束语

本文给出了通用的信息度量定义,简化了CPM软解调算法,进而提出了基于可靠度的低复杂度联合迭代译码算法。该算法采用概率的对数对可靠度进行定义,并以符号/比特的可靠度作为内外译码器之间的迭代信息。仿真结果表明,基于可靠度的低复杂度联合迭代译码算法的性能与概率域下的算法几乎没有差异;在总迭代次数相同的情况下,采用低复杂度联合迭代的性能相比于未采用联合迭代的性能有约0.75 dB的增益。通过对不同调制方式的仿真可以看出,本文提出的算法对相位连续调制具有普适性。同时本文提出的低复杂度联合迭代译码方案可为LDPC码在CPM系统中的应用提供相关的理论参考。

[1] 张韬.一种新颖的Multi-h CPM信号符号速率盲估计算法[J].电讯技术,2012,52(9):1448-1451. ZHANG Tao.A Novel Symbol Rate Blind Estimation Algorithm for Multi-h CPM Signal[J].Telecommunication Engineering,2012,52(9):1448-1451.(in Chinese)

[2] GALLAGER R G.Low-density parity-check codes[M]. Cambridge:MIT Press,1963.

[3] KSCHISCHANG F R,FREY B J,LOELIGER H A.Factor graphs and the sum-product algorithm[J].IEEE Transactions on Information Theory,2001,47(2):498-519.

[4] MACKAY D J C,NEAL R M.Near Shannon limit performance of low-density parity-check codes[J].Electronic Letters,1996,32(18):1645-1646.

[5] MACKAY D J C,WILSON S,DAVEY M.Comparison of constructions of irregular Gallager codes[J].IEEE Transactions on Communications,1999,47(10):1449-1454.

[6] BAHL L R,COCKE J,JELINEK F,et al.Optimal decoding of linear codes for minimizing symbol error rate[J]. IEEE Transactions on Information Theory,1974,20(2): 284-287.

[7] MA X,KAVCIC A.Path partitions and forward-only trellis algorithms[J].IEEE Transactions on Information Theory,2003,49(1):38-52.

[8] MA X,ZHANG K,CHEN H,et al.Low complexity XEMS Algorithms for Nonbinary LDPC Codes[J].IEEE Transactions on Communications,2012,60(1):9-13.

[9] 张凯,杨勇.一种适用于大数逻辑可译LDPC码的自适应译码算法[J].电讯技术,2015,55(1):68-72. ZHANG Kai,YANG Yong.An Adaptive Decoding Algorithm for Majority-Logic Decodable LDPC codes[J].Telecommunication Engineering,2015,55(1):68-72.(in Chinese)

[10] MACKAY D J C.Good error-correcting codes based on very sparse matrices[J].IEEE Transactions on Information Theory,1999,45(2):399-431.

[11] CHEN H,ZHANG K,MA X,et al.Comparisons between reliability-based iterative min-sum and majority-logic decoding algorithms for LDPC codes[J].IEEE Transactions on Communications,2010,59(7):1766-1771.

ZHANG Kai was born in Xi′an,Shaanxi Province,in 1979.He received the Ph.D.degree from Sun Yat-sen University in 2012.He is now a senior engineer and project manager in Xi′an FengHuo Electronic Technology Co.,Ltd..His research concerns signal processing,information theory and channel coding/decoding in communication.

Email:wangshangcaidao@163.com

A Low Complexity Joint Iterative Decoding Algorithm for CPM and LDPC

ZHANG Kai
(Xi′an FengHuo Electronic Technology Co.,Ltd.,Xi′an 710075,China)

The technology of Continuous Phase Modulation(CPM)and Low-Density Parity-Check(LDPC) codes can not only improve the spectrum efficiency,but also decrease the transmit power.However it will increase the complexity of communication system.To solve the problem,this paper proposes a reliabilitybased soft demodulation algorithm.The new algorithm takes the symbol/bit reliability as the information metric between inner decoder and outer decoder.Simulation results show that,the new joint iterative decoding algorithm performs as well as the probabilistic algorithm and has about 0.75 dB gain compared with decoding algorithm without iterations,with equal total local iterations.

LDPC codes;continuous-phase modulation;reliability information;joint iterative decoding

date:2015-04-02;Revised date:2015-06-25

**通讯作者:wangshangcaidao@163.com Corresponding author:wangshangcaidao@163.com

TN911.3

A

1001-893X(2015)12-1390-05

张 凯(1979—),男,陕西西安人,2012年于中山大学获博士学位,现为高级工程师、西安烽火电子科技有限责任公司项目经理,主要研究方向为通信中的信号处理、信息论和信道编译码技术。

10.3969/j.issn.1001-893x.2015.12.014

张凯.低复杂度的连续相位调制与LDPC联合迭代译码算法[J].电讯技术,2015,55(12):1390-1394.[ZHANG Kai.A Low Complexity Joint Iterative Decoding Algorithm for CPM and LDPC[J].Telecommunication Engineering,2015,55(12):1390-1394.]

2015-04-02;

2015-06-25