切比雪夫多项式拟合GPS卫星星历精度分析

杨兴跃，任超，吕东，孙建伟

(1.南阳市城乡规划测绘院，河南 南阳 473000;2.桂林理工大学，广西 桂林 541004;3.广西空间信息与测绘重点实验室，广西 桂林 541004)

1 引 言

GPS 精密星历是由IGS(International GPS Service for Geodynamics)等国际组织发布，它给出了最终星历(IGF)、快速星历(IGR)、超快速星历(IGU)三种类型的星历［1］。他们的轨道采样率都为15 min 或者5 min，而在实际的应用中，接收机的采样率一般为15 s、30 s［2］，甚至更加密集;这就需要对卫星的轨道拟合或者内插，以满足不同的应用需求。

基于GPS 精密星历拟合的方法较多，目前最常用的是Chebyshev 多项式拟合［3］。但是在拟合时，插值节点的选择对最大误差有一定的影响。本文通过选择切比雪夫点和任意选择的时间节点(随机节点)对卫星轨道进行拟合，比较这两种节点拟合的卫星轨道精度，确定拟合节点的最佳选择方案。

2 Chebyshev 多项式拟合的数学模型

由于chebyshev 多项式适用于［－1，1］的区间，因此在进行星历拟合时要先对插值区间进行转化。在［t0，t0+△t］内采用n 阶Chebyshev 多项式拟合时，利用式(1)完成转化。

卫星坐标北方向可以表示为:

式中Ci为Chebyshev 多项式的待求的未知系数，而且拟合东方向和天顶方向坐标的原理与拟合北方向坐标的原理相同。

利用递推关系:

在拟合时间内［t0，t0+△t］选取m ＞n+1 个点，由式(2)可得m 个时刻的拟合坐标x，将拟合坐标x 和已知坐标X 求差可得:

其中B 是T 的m×n 阶矩阵。

根据最小二乘原理可知C=N－1BTPX，其中N=BTPB［4］。将求得的C 代回式(2)，即可求出任意时刻的GPS 卫星的坐标。

根据Chebyshev 多项式Tn(τ)结构，可以看出在区间［－1，1］上多项式图像和Y 轴的交点有n 个，也就是有n 个零点:

和n+1 个极值点

这两组点称为切比雪夫点，他们在插值中有重要作用，是在单位圆上等距分布点的横坐标，也就是说关于插值区间的中点相互对称［5］。利用切比雪夫点插值，可以使插值区间的最大偏差到达最小［6，7］。

3 实例分析

在IGS 网站上下载(．* SP3)精密星历文件［7］。本文选取6 号卫星2012年5月27日的igsl6900．sp3、igrl6900．sp3和igu16900．sp3精密星历为实验数据。

3.1 不同节点选取方法拟合坐标

对IGF、IGR、IGU 三种星历在6 h～12 h 时段内的星历数据进行不同阶次的切比雪夫多项式拟合。将各自的下载星历每15 min的坐标作为已知坐标，采用随机节点和切比雪夫点两种节点选择方法拟合坐标，得到3种星历11 阶～16 阶多项式拟合的坐标最大残差。

IGS 切比雪夫多项式拟合结果残差 表1

分析表1 可知，随着插值节点的增多IGF 和IGR随机插值节点和切比雪夫点的拟合最大残差的差值在缩小，即精度随着阶数的增大而增高。残差的相对比值没有随着阶数的增加而增加，大约保持在2∶1 左右。但是由于随意插值节点选择的随机性，IGU 拟合轨道的最大残差在15 阶时X 坐标为13.81 mm，Y 坐标为12.81 mm产生了较大的差值，Z 坐标偏差值相对较小。两种方法的残差相对比值也超出了2∶1，X 坐标约为4∶1，Y 坐标约为12∶1。Z 坐标约为2∶1这说明在拟合时，节点选择不恰当会对X，Y 方向结果产生很大的影响，使拟合坐标精度急剧下降。

由图1、图2 可以看出，切比雪夫点拟合的坐标残差比较密集，波动相对平稳，在45 min节点时出现X方向的最大残差值，小于2.5 mm。而随机选取节点拟合的坐标残差在部点突出，波动较大。在345 min节点时X 方向的最大残差接近5 mm。将两种方案的X坐标残差进行比较，从图3 可以看出随机选取节点的拟合结果不稳定。

表2 是拟合坐标与相应的IGS 下载坐标差值的RMS值。通过比较我们可以看出当选择随机节点不恰当时，拟合结果的RMS 和切比雪夫点拟合的结果相差很大。特别是IGU 的X，Y 坐标，随机节点和切比雪夫点拟合的RMS 值比值接近10∶1，使高阶次的拟合精度迅速下降。

图1 切比雪夫点拟合残差分布曲线

图2 随机节点拟合残差分布

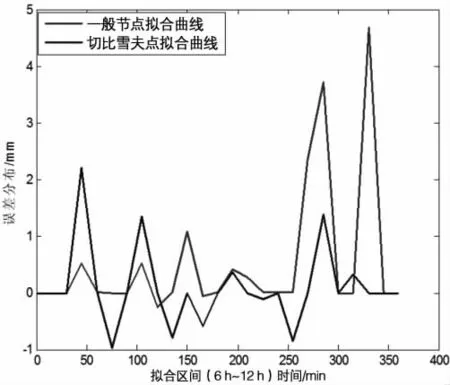
图3 两种节点方案拟合的X 方向的残差

15 阶切比雪夫多项式拟合3 种精密星历的RMS 表2

3.2 切比雪夫点拟合的坐标精度的比较

选取IGS 星历坐标为已知坐标，分别求出IGF，IGR，IGU 的15 阶切比雪夫多项式拟合的坐标精度。从表3 可以看IGF 和IGR 的精度在毫米级，而IGU 的精度都在5 cm的范围以内，比最终星历和快速星历的精度低了一个量级。从图4 可知，选取IGU 中的切比雪夫点拟合的卫星轨道，在X 方向最大残差值小于4 cm，Y 方向最大残差值小于8 cm，Z 方向的最大残差值小于4 cm。

切比雪夫点拟合3 种精密星历的精度对比 表3

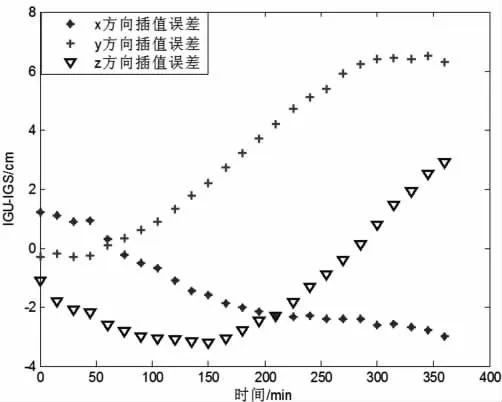
图4 IGU 的拟合精度

4 结 论

(1)在进行拟合时选取切比雪夫点进行拟合卫星坐标残差相对随机选取拟合节点得到的残差分布更均匀，且拟合的最大残差小，即选取切比雪夫点进行多项式拟合可以使插值区间的最大误差最小化。

(2)当拟合的节点选取为非切比雪夫点时，拟合的坐标在X，Y 方向上受到的影响比较大，精度急剧下降。

(3)运用切比雪夫多项式拟合精密星历阶数的增多拟合的轨道精度就越高，15 阶时IGF，IGR 的精度可以达到毫米级，IGU 的精度达到厘米级。

［1］李鹏，熊永良，黄育龙等．GPS 星历精度对精密单点定位的影响［J］．测绘科学，2009，34(2):15～17．

［2］洪樱，欧吉坤，彭碧波．GPS 卫星精密星历和钟差三种内插方法的比较［J］．武汉大学学报·信息科学版，2006，31(6):516～518．

［3］高周正，章红平，彭军还．GPS 卫星星历精度分析［J］．测绘通报，2012(2):1～3．

［4］李明峰，江国焰，张凯．IGS 精密星历内插与拟合法精度的比较［J］．大地测量与地球动力学，2008，28(2):77～79．

［5］彭泽泉．GPS 精密星历拟合方法的研究［J］．测绘科学，2008，35(S):63～65．

［6］李庆扬，王能超，易大义．数值分析［M］．北京:清华大学出版社，2008．

［7］李征航，黄劲松．GPS 测量与数据处理［M］．武汉:武汉大学出版社，2005．