基于图论的道路偶发性局部拥堵区域动态演化
2015-06-27吴义虎屈晓光
吴义虎,谢 芝,喻 伟,喻 丹,屈晓光
(长沙理工大学交通运输工程学院,湖南长沙 410004)
随着城市人口和机动车保有量持续、大幅增加,城市交通设施的规划和建设已不能满足交通需求的变化,城市交通供需矛盾日益尖锐,交通拥堵已成为城市的主要问题之一。除了人们常见的高峰期拥堵外,城市道路网中一些交通事件易造成偶发性交通拥堵。由于偶发性交通拥堵的随机性和衍生性,若处理不及时或控制策略不佳,容易导致城市路网大面积的交通拥堵。
对于高峰期拥堵,对应的交通控制策略是提高通行能力与各交叉口、路段的相互协调。而偶发性交通拥堵发生的地点和时间具有随机性,其疏散控制比较复杂:①由于交通拥堵控制发生的地点具有随机性,其相邻交叉口和路段的通行能力、交通流特性是不同的;②由于发生拥堵的时间具有随机性,不同时段交通流也具有不同的特性。相对常态交通流的优化控制方案,偶发性交通拥堵疏散控制区域的动态划分是将关联程度较大的相邻交叉口合并成一个控制区域,不同的控制区域采用不同的控制策略,由控制系统实施实时控制,达到拥堵快速疏散的控制目标。
学者们针对交通拥堵的疏散控制进行了大量的研究工作。一旦某路段或交叉口发生拥堵,道路通行能力下降,拥堵将向与之相邻的路段和交叉口传播,形成拥堵区域。因此,疏散控制的关键是控制区域的动态划分。Walinchus[1]最先提出了交通控制子区的概念,并将控制子区分界线划在流量特性或道路特性发生显著变化的地段以及行政边界之上;Wilson[2]等人将控制区域划分为若干个独立的小区;莫汉康[3]等人给出了诱导条件下的交通子区动态划分方法,给出了子区划分的周期原则、流量原则和距离原则等;杨晓光[4-6]等人提出了动态交叉口群协调控制理论与方法,并考虑物理关联性和路径关联性,将整个拥堵区域划分为阻塞区、过渡区及常态区。这些研究从拥堵发生时交通流的特性出发,探讨了相邻交叉口关联程度的确定方法。
图论是离散数学的重要分支。随着离散数学和计算机科学的发展,图论在网络分析方面发挥了重要的作用[7]。同样,图论也可应用于道路交通网络中,道路中的交叉口(或节点)通过路段(或线条)连接起来所形成的点和线的关系图即为路网(如图1所示),其实际是描述了物理关联性和路径关联性。图论在处理分类问题上,以其直接明了和简单实用等特点具有相当大的优势[8]。作者拟采用图论的方法,分析拥堵发生时道路交通流动态演化的情况。利用图论中相似度矩阵,对拥堵区域各交叉口交通流状态进行聚类分析,以判断路段或交叉口属于阻塞区、过渡区或常态区。根据不同时刻拥堵区域内交通流的实时状态参数进行聚类分析,动态描述拥堵区域阻塞区、过渡区及常态区的演化过程,将其结果用于控制区域动态划分或城市路网易堵区域的分析,以期对路网规划和拥堵控制提供有用的参考数据。
1 图论的基本概念
图论中的“图”,并非通常意义下的几何图或设计图等,而是以一种抽象的形式来表达一些具体的对象,以及各对象间具有或不具有的某种特定关系的数学模型。直观地说,给出n个点集合V,用直线或曲线集合E将其中的一些点连接起来,这样所形成的点与线的关系结构(V,E)就是一个图G。某路网结构如图2所示,用节点集V={V1,V2,…,V6}表示交叉路口,用边集合E={e1,e2,…,e9}表示各交叉路口间的道路。

图1 某交通路网Fig.1 A road network

图2 某交通路网结构Fig.2 The structure of a road network map
图G的结构也可用一个n×m阶的矩阵X=(xij)n×m表示。图2中交叉口集合V={V1,V2,…,V6}中各交叉口分别具有权值系数,其物理意义为该交叉口拥有的车道数N、t时刻驶向该交叉口的交通流密度P和t时刻该交叉口通行能力C,则图2可表示为:
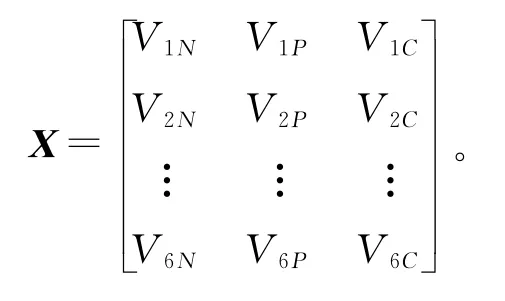
2 基于图论的拥堵区域交通流动态聚类方法
2.1 动态聚类时间间隔
偶发性事件易造成道路拥堵。由于拥堵漂移,拥堵规模也随之变大。然后,随着交通事件的处理与交通控制措施的实施,拥堵逐渐消散。因此,拥堵区域交通流状态变化是一个动态过程。如果为了实现快速疏散控制,需要每隔一段时间对路网交通流参数进行采集并对其状态分别属于阻塞区、过渡区及常态区进行聚类分析。因为拥堵区域是以某个交叉口与其相邻交叉口之间的路段为最小单位,故动态界定拥堵区时间间隔为:

2.2 拥堵区域交通流参数选择和原始矩阵构建

式中:xnm为第n个分类交叉口中第m个参数的原始数据。
对于偶发性局部拥堵区域,交叉口拥堵状态划分是最重要和最基础的。选取能够代表该拥堵程度的参数,反映拥堵状态和发展趋势,用于疏散控制策略的选取。选取3个参数作为拥堵区域动态聚类分析:①连接该交叉口的车道数N;②交叉口通行能力C;③t时刻该交叉口的交通流密度P,其中密度参数为:

2.3 拥堵区域内各交叉口相似度矩阵构造
反映交叉口的交通状态参数类型繁多,且不同参数间的差异较大,因此用相似性法的归一化处理参数间的差异。为了避免对同一聚类问题用不同方法构造相似矩阵时产生较大的聚类差异,本研究采用绝对值指数法构造相似矩阵。在原始矩阵X的基础上,造出n行n列的相似度矩阵R,xk与xl的相似程度为:

式中:rkl为2个样本xk与xt相似程度的变量(rkl越小,表示2个样本越接近)。
2.4 采用Kruskal算法生成最小树
交通路网中道路错综复杂,交叉口之间通过不同的道路相连接。若依次对每个通过道路相连的交叉口进行聚类分析,其计算工作量太大。因此,去除相似度较大的交叉口间的道路连接,从而排除两交叉口间的关联较少而没必要进行的聚类分析。克鲁斯卡尔(kruskal)算法用于生成最小树可以解决这一问题。它是在原有n个交叉路口(或顶点)的连通交通网络G=(V,R)中,最初先构造一个只有n个交叉口(或顶点),没有道路(或边)相连的非连通图M={V,Φ},图中每个交叉口自成一个连通分量。然后,在待选道路R中选取一条rkl最小的道路。若该道路的两个顶点落在不同的连通分量上,则将此边加入到最小树道路集合J0中;否则,将此边舍去,重新选择另一条rkl较小的边。如此重复下去,直到所有顶点在同一个连通分量上为止。此时得到的最小树集合图则为最终聚类结果。虽然用Kruskal法得出的最小树不唯一,但聚类结果是唯一的。给定赋权连通图G=(V,R),Kruskal算法步骤为:
1)开始原顶点集合V=(v1,v2,...,vn),且顶点集合对应的边的权值矩阵

生成的最小树顶点集合T0={},生成的最小树边集合J0={}。
4)重复3),直至J=V,则结束运算,所得最小树集合为J。
2.5 交通流状态聚类
求出最小树J后,根据rkl的大小确定各区域间的相互关系。本研究选定的3个参数中,交通流密度P可直观地反映拥堵状态;交叉口通行能力C和道路车道数N为道路物理参数,二者的大小对拥堵传播速度产生的影响是:通行能力和车道数越大,拥堵传播速度越快。其原因是:车道数越多的道路和通行能力越大的交叉口,其车流量也越大,偶发性拥堵传播的速度也越大。因此rkl的大小既综合描述了拥堵状态,又反映了交通流状态变化趋势。距事故发生地点较近的路段和交叉口,其拥堵程度越大。以事故发生点为中心由内而外的区域,交通流状态依次是阻塞区、过渡区及常态区,而且3个区域的空间形状不一定规则。
相似程度的变量rkl阈值的确定应参考实际交通情况而定。rkl越小,说明2交叉口间的相似度越大,交通拥堵状况越严重。根据实际交通情况,假设:当rkl≤0.65时,两相邻交叉口可合并为交通阻塞区;当0.65<rkl≤1时,两相邻交叉口可并为交通过渡区;当rkl>1时为交通常态区。
3 仿真结果与分析
为了检验基于图论的城市道路偶发性交通拥堵区域交通流状态聚类分析方法的有效性和稳定性,以某城市道路网络突发交通事件为例,利用Matlab进行仿真实验。设定偶发性事故发生地点处于某条双向6车道,在由南往北方向上,事故占用两个车道,且该路段中间隔离设施优良,事故发生后不会对对向道路通行能力产生影响。依次设定该路段区域路网参数,偶发性交通发生10min后,该事故区域交叉口的原始参数见表1。

表1 相关系数及划分结果Table 1 The correlation coefficient and the divided the result
在Matlab中,将基于图论的Kruskal方法与FCM算法分别进行聚类分析,并比较计算结果。因为FCM方法是被验证过的有效的聚类分析方法,若二者差别不大,则证明图论Kruskal算法是有效可行的。表1是由图论Kruskal方法和FCM聚类方法计算得到的各交叉路口相似程度的变量及各子区交通流状态结果。
表1中,由图论Kruskal方法与FCM聚类方法计算得到的输出交叉路口相似程度值和交通流状态结果相似,故基于图论的Kruskal方法用于拥堵区域交通流状态演化分析是可行的。偶发性事件发生10min后,拥堵区域交通流状态如图3所示。

图3 偶发性事件区域交通划分结果Fig.3 The division scheme of the region with accidental incidents
该偶发性事件发生15min后,若不采用任何的控制措施下,再次用图论Kruskal方法得到的该拥堵区域交通流状态如图4所示。
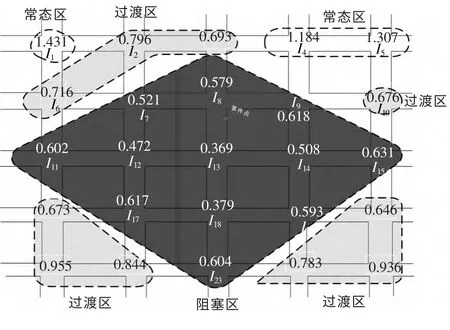
图4 不采取控制措施下拥堵区域范围变化Fig.4 The change of average queue length without any strategies for the heavy traffic region
从图3和图4中可以看出,偶发性事件发生后,该路段通行能力下降,造成了交通拥堵。出行者根据其出行目的地,由拥堵区域上游驶入拥堵区域,进入了该区域相应的排队区域。由于下游路段通行能力下降,拥堵区域将通过交叉口由下游路段后溢至上游相邻的交叉口。故交通拥堵区域在空间上呈菱形,距事件点交通流密度较大的交叉口和路段为菱形的长轴,距事件点交通流密度较小的交叉口和路段为菱形的短轴。随着时间的增加,拥堵区菱形面积增大。
4 结论
1)提出了一种利用图论的相似度矩阵,对拥堵区域各交叉口交通流状态采用聚类分析方法,以判断路段或交叉口属于阻塞区、过渡区或常态区。根据不同时刻拥堵区域内交通流的实时状态参数进行了聚类分析,动态描述了拥堵区域阻塞区、过渡区及常态区的演化过程,数值仿真结果表明:该方法可行,与实际交通拥堵发生造成交通流变化情形吻合,该方法具有交通流状态演化结果直接明了和简单实用等特点。
2)初步仿真结果表明,偶发性事件发生后,事发路段通行能力下降,出行者根据其出行目的地,由事发路段上游驶入拥堵区域,进入了该区域相应的排队区域。交通拥堵区域在空间上呈菱形,距事件点交通流密度较大的交叉口和路段为菱形的长轴,距事件点交通流密度较小的交叉口和路段为菱形的短轴。随着时间的增加,拥堵区将沿菱形长、短轴蔓延。
3)采用图论方法分析拥堵发生时道路交通流状态演化情况,其结果可以用于城市交通拥堵控制区域动态划分,也可以用于城市路网易堵区域的分析,为路网规划和拥堵控制策略的选择提供依据。
(References):
[1]Walinchus R J.Real-time network decomposition and sub-network interfacing[J].Highway Research Record,1971(366):20-28.
[2]Wilson D R,Martinez T R.Improved heterogeneous distance functions[J].Journal of Artificial Intelligence Research,1997,6:1-34.
[3]莫汉康,彭国雄,云美萍.诱导条件下的交通控制子区自动划分[J].交通运输工程学报,2002,2(2):67-72.(MO Han-kang,PENG Guo-xiong,YUN Meiping.Automatic division of traffic control sub-area under condition of route guidance[J].Journal of Traf-fic and Transportation Engineering,2002,2(2):67-72.(in Chinese))
[4]段后利,李志恒,张毅,等.交通控制子区动态划分模型[J].吉林大学学报:工学版,2009,39(S2):13-18.(DUAN Hou-li,LI Zhi-heng,ZHANG Yi,et al.Dynamic subdivision of road network into coordinated control regions[J].Journal of Jilin University:Engineering and Technology Edition,2009,39(S2):13-18.(in Chinese))
[5]杨晓光,黄玮,马万经.过饱和状态下交通控制小区动态划分方法[J].同济大学学报:自然科学版,2010,38(10):1450-1457.(YANG Xiao-guang,HUANG Wei,MA Wan-Jing.Method of delimiting urban traffic signal coordinated control subarea under oversaturated condition[J].Journal of Tongji University:Natural Science Edition,2010,38(10):1450-1457.(in Chinese))
[6]卢凯,徐建闽,李轶舜.基于关联度分析的协调控制子区划分方法[J].华南理工大学学报:自然科学版,2009,37(7):6-9.(LU Kai,XU Jian-min,LI Yishun.Division method of coordinated control subareas based on correlation degree analysis[J].Journal of South China University of Technology:Natural Science Edition,2009,37(7):6-9.(in Chinese))
[7]杨庆芳,陈林.交通控制子区动态划分方法[J].吉林大学学报:工学版,2006,36(增刊2):139-142.(YANG Qing-fang,CHEN Lin.Division approach of traffic control work zone[J].Journal of Jilin University:Engineering and Technology Edition,2006,36(Supple2):139-142.(in Chinese))
[8]邱关源.网络图论简介[M].北京:人民教育出版社,2002.(QIU Guan-yuan.The introduction of network graph theory[M].Beijing:People’s Education Press,2002.(in Chinese))
[9]耿素云.集合论与图论[M].北京:北京大学出版社,1998.(GENG Su-yun.Set theory and graph theory[M].Beijing:Beijing University Press,1998.(in Chinese))
[10]肖位枢.图论及其算法[M].北京:航空工业出版社,1993.(XIAO Wei-shu.Graph theory and algorithms[M].Beijing:Aviation Industry Press,1993.(in Chinese))
[11]曹建农,方丹霞.基于图论的图像分割方法及其局限性研究[J].测绘技术装备,2006(2):12-15.(CAO Jian-nong,FANG Dan-xia.The image segmentation method based on graph theory and its limitations[J].Geomatics Technology and Equipment,2006(2):12-15.(in Chinese))
[12]张敖木翰,高自友,任华玲.突发事故下交通拥堵控制策略[J].中国科学:技术科学,2011,41(7):955-961.(ZHANG Ao-mu-han,GAO Zi-you,REN Hualing.Incident-based traffic congestion control strategy[J].Science China:Technology Science,2011,41(7):955-961.(in Chinese))
[13]张敖木翰.突发事件下非重复性交通拥堵传播规律与控制策略研究[D].北京:北京交通大学,2012.(ZHANG Ao-mu-han.Studies on properties and control strategies of incident-based non-recurrent traffic congestion propagation[D].Beijing:Beijing Jiaotong University,2012.(in Chinese))
[14]王炜,过秀成.交通工程学[M].南京:东南大学出版社,2011.(WANG Wei,GUO Xiu-cheng.Traffic engineering[M].Nanjing:Southeast University Press,2011.(in Chinese))
