基于曲波变换的地震反射波同相轴斜率拾取方法
2015-06-27金昌昆蒋亚洲张建中
金昌昆,蒋亚洲,张建中
(1.海底科学与探测技术教育部重点实验室,山东青岛266100;2.中国海洋大学海洋地球科学学院,山东青岛266100)
基于曲波变换的地震反射波同相轴斜率拾取方法
金昌昆1,2,蒋亚洲1,2,张建中1,2
(1.海底科学与探测技术教育部重点实验室,山东青岛266100;2.中国海洋大学海洋地球科学学院,山东青岛266100)
局部相关反射波同相轴的斜率反映了射线参数、慢度水平分量等地震波运动学信息,被用于地下速度建模和偏移成像等地震数据处理中。拾取反射波同相轴斜率是应用斜率数据的必然环节。提出了一种基于曲波变换(Curvelet transform)的地震反射波同相轴斜率拾取方法。该方法根据曲波变换所具有的各向异性和局部方向性的性质,利用地震信号曲波变换后的曲波系数,确定地震反射同相轴位置和延伸方向,再将延伸方向换算成斜率值。理论数据测试和实际地震资料试应用结果表明,与常用的基于倾斜叠加以及直线—双曲线叠加的反射波同相轴斜率拾取方法相比,该方法具有更高的精度。
曲波变换;反射波同相轴;斜率拾取;倾斜叠加;直线—双曲线叠加
地震反射波同相轴斜率是指在地震记录道集(如共炮点道集、共接收点道集)上,来自同一反射界面的局部相关同相轴在某道上的切线的斜率,也就是该道上的反射走时沿测线方向的梯度,它反映了射线参数和慢度水平分量。同相轴斜率包含了反射波几何信息,因此许多学者研究了利用斜率数据进行地震资料的处理和成像。Hua等[1-2]利用炮点的斜率获取射线角,提出了计算效率很高的二维和三维偏移方法;Hertwech等[3]把斜率参数用于共反射面元叠加中;Fomel[4]和Cooke等[5]应用斜率进行独立于速度模型的时间偏移成像;杜婧等[6]研究了基于斜率的VSP波场分离;Billette等[7]把炮点、接收点的斜率和双程走时作为观测数据,提出基于斜率的立体层析成像方法;倪瑶等[8]对立体层析成像方法进行了应用测试;Guillaume等[9]研究了共偏移距矢量道集的斜率层析成像方法。
在这些方法及其应用中,斜率的拾取是不可或缺的环节,而且斜率数据的精度必然影响着它们的应用效果。目前,斜率拾取主要采用倾斜叠加技术(slant stack)[10-11]。然而,在同相轴的线性程度不高时,利用倾斜叠加技术拾取斜率的效果往往不佳;特别是在近偏移距,局部同相轴变化的线性程度往往很低,用倾斜叠加方法拾取斜率的误差较大。为此,黄忠来等[12]提出了一种基于直线—双曲线叠加的斜率拾取方法。在共偏移距域用线性叠加方法拾取中心点上的斜率值,在共中心点域用双曲线叠加方法拾取半偏移距位置上的斜率值,然后把中心点和半偏移距上的斜率值换算成炮点和接收点上的斜率值。模型数据和实际资料的测试结果证明此方法比倾斜叠加方法具有更高的精度。
曲波变换是Candès等[13]于1999年提出的一种多尺度变换方法,它也是一种多分辨、带通、具有方向性的函数分析方法。2002年,Candès等[14]又提出了第二代曲波变换的框架系,2005年提出了两种快速离散曲波变换方法[15],即非均匀快速傅里叶变换(Unequally-spaced FFT,USFFT)和基于Wrapping算法。相对于第一代曲波变换,第二代曲波变换具有概念更简洁、运算速度更快、冗余性更小等优点。曲波变换具有的局部性、多尺度性和多方向性,可以用来较好地表征地震数据的局部特征[15],从而越来越多地被应用于地震资料处理。Herrmann等[16]提出了全新的基于曲波变换的地震数据处理的概念;Neelamani等[17]利用曲波变换压制地震相干噪声和随机噪声;张恒磊等[18]提出在曲波域采用非线性阈值方法对叠前地震资料随机噪声进行压制;Mansour等[19]利用曲波变换实现了海上随机采样及数据重构;刘国昌等[20]利用曲波变换进行地震数据的缺失道插值;Hubb等[21]把曲波变换应用于地震成像中;张广智等[22]利用曲波变换的多尺度性识别裂缝发育带。
地震反射同相轴斜率拾取需要自动追踪来自同一反射界面的局部相关同相轴,并确定该同相轴的延伸方向。根据曲波变换具有的局部性和方向性的优势,本文提出一种基于第二代曲波变换的地震同相轴斜率拾取方法,通过理论合成数据和实际地震资料的测试应用,并与基于倾斜叠加的方法和基于直线—双曲线叠加的方法对比,验证本文方法的有效性。
1 方法原理
函数f(t1,t2)∈L2的离散曲波系数[15]表示为:
(1)
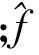
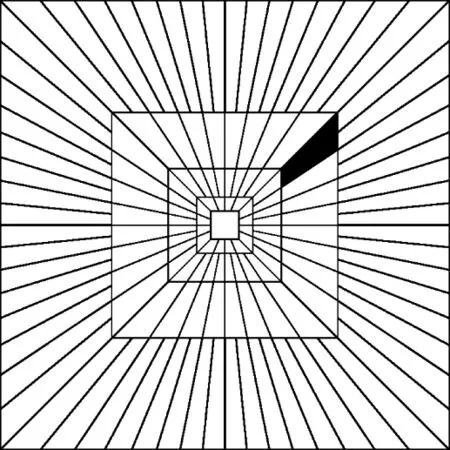
图1 离散曲波空间频率域区域分块示意
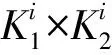
(2)

把每一层尺度ji上的曲波系数cjilk投影到尺度jp的网格gp中,尺度ji上网格点坐标投影到尺度jp的网格gp的子集Ai,p(k)中[23],有:
(3)
同理,把尺度ji上的方向参数l投影到尺度jp中的方向参数Lp的子集Di,p(l)中,有:
(4)
式中:Li是尺度ji上总的方向个数;Lp是尺度jp上总的方向个数。
在选取的jp层中的每个方向l和坐标k=(k1,k2)上,计算曲波系数的模值和大小:
(5)
(5)式中计算Mlk时,方向参数l只需从1变化到Lp/2即可,这是因为l和l+Lp/2相差180°,实际表示同一个方向。一般情况下求出Mlk后,就可以得到在每一个网格点k=(k1,k2)上的主方向l0(k)以及主方向对应的最大曲波系数值Mlk,即:
(6)
根据Mlk来判断同相轴振幅极大值位置,如果Mlk0是每一道地震记录曲波系数的模值Mlk的局部极大值,且系数Mlk0大于一定的阈值,坐标k0便是同相轴振幅极大值位置,此时此点同相轴斜率值为:
(7)
式中:θl0是方向参数l0对应的角度值;Δt是地震记录时间采样率;Δx是地震记录的道间距。
算法的实现流程如下。
1) 读入地震记录,选出将要求取的同相轴斜率的地震记录。
2) 进行曲波变换。采用Wrapping算法对数据进行变换,得到曲波系数。
3) 提取位置和方向参数。选取合适的曲波系数,求取同相轴坐标位置和对应位置方向参数。
4) 由(7)式计算该点上的斜率值。
2 模型测试与实际资料试应用
2.1 两层水平均匀介质模型理论数据
首先选用能够直接求得炮点和接收点的理论斜率值的模型数据进行测试分析,以便对用本文方法自动拾取的同相轴斜率值与理论斜率值进行比较。图2所示是一个简单的两层水平均匀介质模型。炮点S坐标为xs,接收点R的坐标为xr,上层介质速度为v1,下层介质速度为v2,则一次反射波时距方程可表示为[24]:
(8)
这样,接收点pr的斜率值为:
(9)
图2所示模型中炮点坐标S为坐标原点,接收点与炮点距离为x。界面深度h=200m,取v1=1000m/s,v2=2000m/s,根据公式(9)计算接收点上的理论斜率值pr。
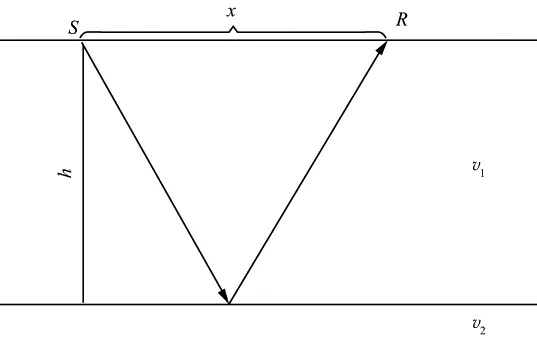
图2 两层水平均匀介质模型
同时基于褶积模型合成该模型的单炮地震记录数据。其中,地震子波用Ricker子波,中心频率30Hz,均匀布设256个接收点,接收点间距10m,中心点放炮,每道采样点数为1024,采样周期为2ms。合成的共炮点地震记录如图3所示。对该合成记录用倾斜叠加方法(叠加窗空间长度为9道)直接拾取接收点的斜率值pr,如图4中的虚线所示。再应用本文方法确定各道同相轴的位置及斜率值pr,其中,取Lp=256,即在尺度jp中的方向数为256个,拾取结果如图4中的点线所示。图5 是这两种方法拾取的斜率值相对计算理论值的误差曲线。从图中可以看出,由于近偏移距处的斜率值较小以及时距曲线曲率较大,两种方法在近偏移距处的误差都明显大于远偏移距处的误差;但即使在近偏移距处,本文方法拾取斜率值的精度也明显高于倾斜叠加方法。

图3 两层水平介质模型的合成地震记录
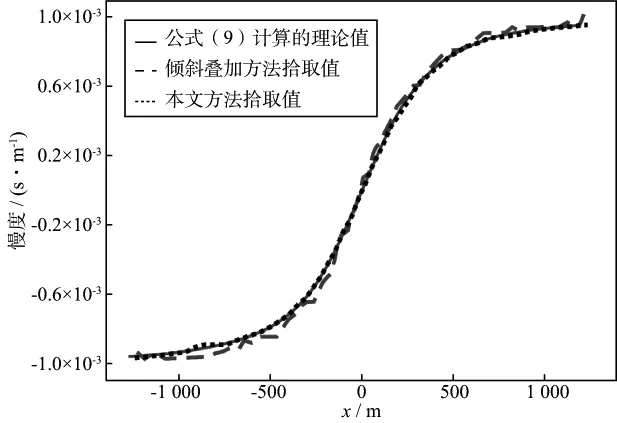
图4 计算与拾取的两层模型各接收点的斜率值
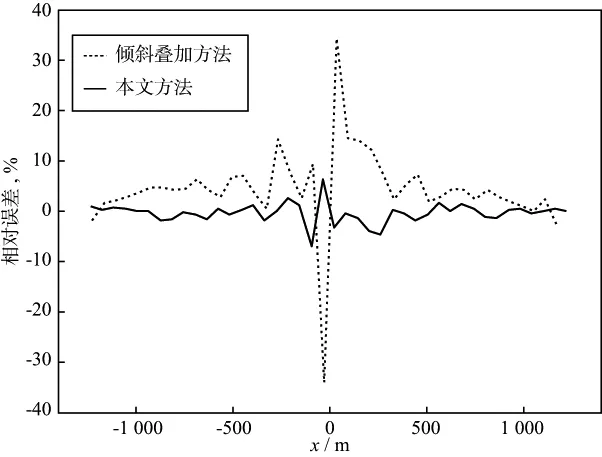
图5 图4中两种拾取值相对于理论值的误差
一般地,曲波变换的方向数越多,斜率拾取的精度越高。图6所示为方向数分别取64和512时拾取结果在偏移距250~1000m的相对误差。可见偏移距小于300m时,两种结果的相对误差都比较大;在300~550m,方向数为64时拾取斜率误差(虚线)要大一些;方向数为512时拾取结果的误差(实线)在偏移距400m左右基本稳定,而方向数为64的结果误差在偏移距大于500m时才趋于稳定;当偏移距大于550m时,走时斜率较大,两种方法拾取结果的误差均很小。由此可以看出,当方向数较少时,所得结果的误差较大。
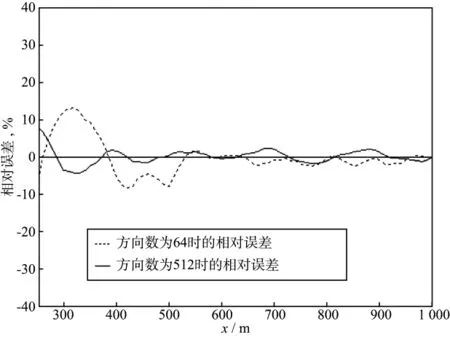
图6 取不同方向数时拾取结果的相对误差
2.2 Marmousi模型声波方程模拟数据
对Marmousi模型用声波方程模拟(道间距25m,采样周期4ms)得到的地震数据[7],首先计算其理论斜率值。取出某个反射同相轴的走时,在一个包含9道的窗口内用二次曲线拟合反射走时,对拟合的二次曲线求导获取共炮域各接收点的走时沿测线方向的导数,这样求得的导数值即可看作理论斜率值,作为其它方法拾取结果比较的参考基准。
然后采用3种不同方法拾取模拟数据炮点和接收点的斜率值。第1种是用常规的倾斜叠加方法(叠加窗空间长度为9道,时间窗口为40采样点)在共炮域拾取接收点的斜率;第2种是文献[12]提出的基于直线—双曲线叠加的斜率拾取方法;第3种是用本文的曲波变换方法(方向参数Lp=256)进行拾取。这里给出第32炮记录的一个反射同相轴的拾取结果。
图7箭头指示拾取的反射同相轴;图8是分别采用倾斜叠加方法、直线—双曲线叠加方法和本文方法拾取的斜率值与理论斜率值的对比;图9是3种方法分别拾取的斜率值相对理论斜率值的相对误差。可以看出,本文方法可应用于复杂模型数据,并且比倾斜叠加方法及直线—双曲线叠加方法具有更高的拾取精度。
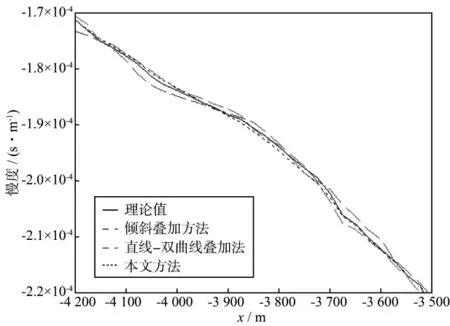
图8 图7箭头所示同相轴对应的斜率值
2.3 实际地震资料试应用
对经过去噪和静校正等常规处理后的某复杂地形条件下的实际地震资料(道间距15m,采样周期4ms),采用上述3种方法拾取同相轴斜率。其中,通过对同相轴进行二次曲线(9点)拟合再求导数,并把求得的导数值作为与其它方法结果进行比较时的理论斜率值;常规的倾斜叠加方法取叠加窗道数为9道;本文方法拾取时的方向参数Lp取256。这里给出第82炮记录中的两个反射同相轴(见图10中箭头所示)的斜率拾取结果。图10 是实际地震资料第82炮的记录;图11是3种方法拾取结果与理论值的对比;图12是3种方法拾取结果的相对误差。由图10,图11和图12可见,由于实际地震资料中含有噪声干扰,倾斜叠加方法的拾取结果(图11中绿线)明显受到了噪声的影响,斜率值曲线具有相对剧烈的跳跃变化;直线—双曲线叠加斜率拾取方法比较稳定,相对误差平均为2.1%(图12中蓝实线);本文方法拾取的斜率值曲线(图11中蓝线)无明显的跳跃现象,与理论值更符合,平均误差为1.8%(图12中黑实线)。
实际资料试应用的结果表明,本文基于曲波变换的斜率拾取方法比基于倾斜叠加及直线—双曲线叠加的斜率拾取方法具有更高的拾取精度以及较强的抗噪能力。
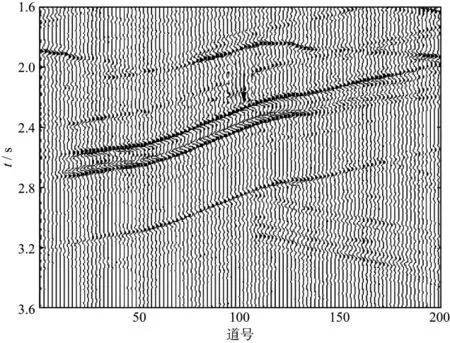
图10 实际地震资料第82炮的地震记录(箭头标注的是3种方法拾取的同相轴)
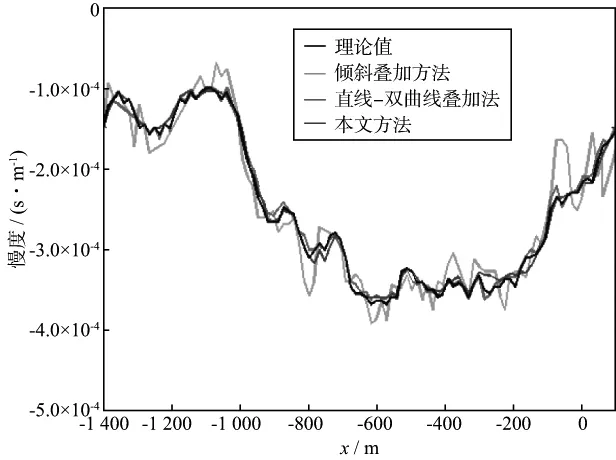
图11 图10箭头所示同相轴对应的斜率值
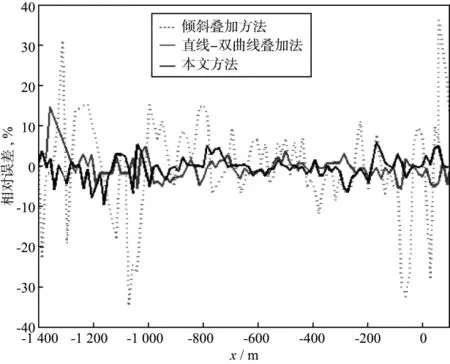
图12 图11中3种方法拾取值相对于理论值的误差
3 结论与认识
根据曲波变换的各向异性和局部方向性的性质,对地震记录进行曲波变换,利用所得到的曲波系数,可以准确确定反射同相轴位置和延伸方向等参数,从而提出了一种基于曲波变换的地震反射同相轴斜率拾取方法。与常用的倾斜叠加方法相比较,倾斜叠加方法拾取同相轴斜率需要选择合适的窗口长度,窗口长度对拾取斜率的精度影响很大,而本文方法拾取同相轴斜率是对全部地震数据进行曲波变换,在空间方向上无需选择窗口。理论合成数据测试和实际地震资料试应用的结果表明,本文提出的基于曲波变换的同相轴斜率拾取方法比常用的倾斜叠加方法和直线—双曲线叠加斜率拾取方法具有更高的精度和更强的抗噪能力。此外,本文方法拾取斜率的精度与曲波变换所选取方向数的多少有关,方向数越多,对同相轴方向的检测精度越高,从而拾取斜率的精度也越高。
[1] Hua B,McMechan G A.Parsimonious 2D prestack Kirchhoff depth migration[J].Geophysics,2003,68(3):1043-1051
[2] Hua B,McMechan G A.Parsimonious 3D post-stack Kirchhoff depth migration[J].Geophysical Prospecting,2005,53(4):507-522
[3] Hertwech T,Schileicher J,Mann J.Data stacking beyond CMP[J].The Leading Edge,2007,26(7):818-827
[4] Fomel S.Velocity-independent time-domain seismic imaging using local event slopes[J].Geophysics,2007,72(3):S139-S147
[5] Cooke D,Bóna A,Hansen B.Simultaneous time imaging,velocity estimation,and multiple suppression using local event slopes[J].Geophysics,2009,74(6):WCA65-WCA73
[6] 杜婧,王尚旭,刘国昌,等.基于局部斜率属性的VSP波场分离研究[J].地球物理学报,2009,52(7):1867-1872 Du J,Wang S X,Liu G C,et al.VSP wavefield separation using local slope attributes[J].Chinese Journal of Geophysics,2009,52(7):1867-1872
[7] Billette F,Lambaré G.Velocity macro-model estimation from seismic reflection data by stereotomography[J].Geophysical Journal International,1998,135(2):671-690
[8] 倪瑶,杨锴,陈宝书.立体层析反演方法理论分析与应用测试[J].石油物探,2013,52(2):121-130 Ni Y,Yang K,Chen B S.Stereotomography inversion method:theory and application testing[J].Geophysical Prospecting for Petroleum,2013,52(2):121-130
[9] Guillaume P,Montel J P,McCarthy A,et al.Non-linear slope tomography from common offset vector volumes as applied to a high density land WAZ survey from the Sultanate of Oman[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010,4395-4399
[10] Lambaré G,Alerini M,Baina R,et al.Stereotomography:a semi-automatic approach for velocity macromodel estimation[J].Geophysical Prospecting,2004,52(6):671-681
[11] Lambaré G,Alerini M,Podvin P.Stereotomographic picking in practice[J].Expanded Abstracts of 74thAnnual Internat SEG Mtg,2004,2343-2346
[12] 黄忠来,张建中,蒋亚洲.基于直线和双曲线叠加的斜率自动拾取方法[J].地球物理学进展,2013,28(6):3007-3014 Huang Z L,Zhang J Z,Jiang Y Z.Automatic method for picking slopes of locally coherent events based on linear and hyperbolic stack[J].Progress in Geophysics,2013,28(6):3007-3014
[13] Candès E J,Donoho D L.Curvelets:a suprisingly effective nonadaptive representation for objects with edges,in curves and surface fitting:saint-malo 1999[M].Nashville:Vanderbilt University Press,2000:105-120
[14] Candès E J,Donoho D L.New tight frames of curvelets and optimal representations of objects with smooth singularities[D].USA:Department of Statistics,Stanford University,2002[15] Candès E J,Demanet L,Donoho D L,et al.Fast discrete curvelet transform[J].Multiscale Modeling and Simulation,2005,5(3):861-899
[16] Herrmann F J,Wang D L,Hennerfent G.Curvelet-based seismic data processing:a multiscale and nonlinear approach[J].Geophysics,2008,73(1):A1-A5
[17] Neelamani R,Baumstein A I,Gillard D G.Coherent and random noise attenuation using the curvelet transform[J].The Leading Edge,2008,27(2):240-248
[18] 张恒磊,刘天佑,张云翠.基于高阶相关的Curvelet域和空间域的倾角扫描噪声压制方法[J].石油地球物理勘探,2010,45(2):208-214 Zhang H L,Liu T Y,Zhang Y C.High order correlation based dip angle scanning noise elimination method in Curvelet domain and space domain[J].Oil Geophysical Prospecting,2010,45(2):208-214
[19] Mansour H,Wason H,Herrmann F J.Randomized marine acquisition with compressive sampling matrices[J].Geophysical Prospecting,2012,60(4):648-662
[20] 刘国昌,陈小宏,郭志峰.基于Curvelet变换的缺失地震数据插值方法[J].石油地球物理勘探,2011,46(2):237-246 Liu G C,Chen X H,Guo Z F.Missing seismic data rebuilding by interpolation based on Curvelet transform[J].Oil Geophysical Prospecting,2011,46(2):237-246
[21] Huub D,Hoop M V.Leading-order seismic imaging using curvelets[J].Geophysics,2007,72(6):S231-S248
[22] 张广智,郑静静,印兴耀.基于Curvelet变换的多尺度性识别裂缝发育带[J].石油地球物理勘探,2011,46(5):757-762 Zhang G Z,Zheng J J,Yin X Y.Identification technology of fracture zone and its strike based on the Curvelet transform[J].Oil Geophysical Prospecting,2011,46(5):757-762
[23] Gebäck T,Koumoutsakos P.Edge detection in microscopy images using curvelets[J].BMC Bioinformatics,2009,10(1):1-14
[24] 陆基孟.地震勘探原理[M].北京:石油工业出版社,1982:22-23 Lu J M.The principle of seismic prospecting[M].Beijing:Petroleum Industry Press,1982:22-23
(编辑:朱文杰)
An automatic picking method for slopes of locally coherent reflection events based on Curvelet transform
Jin Changkun1,2,Jiang Yazhou1,2,Zhang Jianzhong1,2
(1.KeyLaboratoryofSubmarineGeociencesandProspectingTechniques,MinistryofEducationofChina,Qingdao266100,China;2.CollegeofMarineGeosciences,OceanUniversityofChina,Qingdao266100,China)
The slopes of locally coherent reflection events represent ray parameters or slowness horizontal components and other kinematic information,which are used in seismic data processing,such as velocity model building,migration imaging,and etc.Picking slopes of reflection events is an essential step in seismic data processing.An automatic picking method is proposed for slopes of reflection events based on Curvelet transform.Based on the characteristics of local directionality and anisotropy for Curvelet transform,the method use the Curvelet coefficients from seismic data transformed by fast discrete Curvelet transform to obtain the location and direction of locally coherent reflection events.And the slopes are finally estimated from the above directions.The tests with both synthetic and field data show that this method has a higher precision compared with either the existing slant stack method or linear-hyperbolic stack method.
Curvelet transform,reflection events,slope picking,slant stack,linear-hyperbolic stack
2014-04-17;改回日期:2014-09-15。
金昌昆(1987—),男,博士在读,研究方向为地震资料处理和层析反演。
张建中(1963—),男,教授,主要从事地球物理勘探方法研究工作。
国家自然科学基金项目(41074077、41230318)资助。
P631
A
1000-1441(2015)04-0414-06
10.3969/j.issn.1000-1441.2015.04.007
