基于压缩感知的稀疏脉冲反射系数谱反演方法研究
2015-06-27陈祖庆王静波
陈祖庆,王静波
(中国石油化工股份有限公司勘探分公司,四川成都610041)
基于压缩感知的稀疏脉冲反射系数谱反演方法研究
陈祖庆,王静波
(中国石油化工股份有限公司勘探分公司,四川成都610041)
基于压缩感知稀疏信号采样和重构理论提出了一种稀疏脉冲反射系数谱反演方法。在稀疏地层假设下,利用地震资料的部分谱信息,采用基追踪算法,反演地下地层在L1范数意义下的宽带稀疏脉冲反射系数。利用褶积宽频带的四参数Morlet子波,生成高分辨率地震剖面,提高地震资料对薄层的识别能力。一维理论模型试验结果证实了利用地震资料的部分谱信息可以准确地反演出稀疏脉冲反射系数序列。二维理论模型试验结果表明,得到的反演结果不仅能识别薄(互)层界面、透镜体边界和地层尖灭位置等薄层结构,还能保持原始地层模型的横向连续性特征,并且具有一定的抗噪性。最后,实际资料的应用结果显示,反演得到的高分辨率剖面不仅在整体地层格架上忠实于原始地震资料,而且能够分辨出原始地震记录中无法识别的薄层结构,使得地下地层的接触关系更加清晰,为地震地层学精细解释提供依据。
压缩感知;稀疏脉冲反射系数;谱反演;L1范数;基追踪;Morlet子波;高分辨率
近年来,随着岩性油气藏勘探的深入,人们对地震资料分辨率的要求越来越高。然而由于实际地震资料高频和低频信息的缺失,传统的最小平方反褶积或谱白化只能恢复反射系数在地震频带范围内的频谱信息,获得带限的反射系数,并不能从根本上拓宽地震资料的频带宽度,获得脉冲状的宽频带反射系数,难以准确分辨调谐厚度以下的薄储层、透镜状单砂体以及地层岩性尖灭位置[1]。因此,从带限或窄带地震资料中重构地震频带以外的反射系数的频率成分,获得宽频带的脉冲反射系数来识别薄层是地震资料解释性处理的一个基本目标。
Vetterli[2]提出了非带限信号的有限更新率采样和重构理论,论证了从带限采样后的窄带信号中重构出非带限的宽带脉冲流的信号的可行性,打破了香农采样定理的局限性。Donoho等[3-4]提出的压缩感知稀疏信号采样和重构理论,进一步论证了稀疏信号经带限采样后形成的窄带非稀疏信号可以在一定条件下被压缩重构为原始的稀疏信号。基于上述理论,Maravic等[5]利用稀疏分布的脉冲流信号的带限采样信号的部分谱信息,利用奇异值分解算法实现了原始稀疏脉冲流信号的重构。这为从有限带宽的地震资料中反演出稀疏的脉冲状宽带反射系数提供了理论基础。显然,稀疏性假设是重构宽频带脉冲反射系数的一个基本的先验假设。在此假设下,反射系数的反演或反褶积问题就归结为求取稀疏的非零反射系数。通常的做法就是通过求解某种稀疏范数的优化问题来强迫反射系数的解稀疏[6]。由压缩感知稀疏信号采样和重构理论可知[3-4],求取稀疏解的最佳稀疏约束范数是零范数,但求解零范数极小化的启发式贪婪算法[7-8],结果容易陷入局部最优,且对噪声比较敏感,随着数据长度的增加计算量迅速增加。因此,通常采用求解L1范数的极小值作为零范数的凸近似来获得稀疏解。由于L1范数带有绝对值算子,目标泛函无法直接求导,因此求解L1范数极小化的问题就成为一个高度非线性的优化问题,需要将该问题转化为线性规划问题,回避L1范数的绝对值算子的影响。Chen等[9]在此思想的基础上,结合原对偶对数障碍法[10],提出了一种求解大型线性规划问题的基追踪算法。该算法能够高效快速地求解大型矩阵方程的L1范数稀疏解问题,并且具有一定的抗噪性。
在上述理论的基础上,推导了褶积模型的谱方程,采用基追踪算法求解反射系数在L1范数极小下的稀疏解,实现从地震资料的部分谱中重构出宽频带的稀疏脉冲反射系数,并结合宽频带的四参数Morlet子波弱旁瓣、保低频和压制高频噪声的特性[11],生成高分辨率地震剖面。通过一维、二维稀疏脉冲反射系数理论模型的试验和实际资料的应用,分析了该方法在识别透镜状砂体边界、薄互层分界面以及地层岩性尖灭位置等薄层结构中的应用效果,并与传统的最小平方反褶积处理效果进行了对比。
1 方法原理
地下地层反射系数时间序列r(t)可以表示为:
(1)
式中:N为地震数据的采样点个数;an和τn分别是第n个采样点上反射系数的振幅和时间位置;δ(t)为脉冲函数。显然,当地层为稀疏且有K个反射界面时,则多数采样点上的反射系数的幅值为零,即非零脉冲反射系数的个数K≪N。
由褶积模型,地震信号s(t)可写成:
(2)
对(2)式进行傅里叶变换,则有褶积模型的频域谱方程:
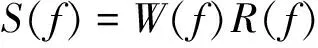
(3)
式中:f为频率;S(f),W(f)和R(f)分别是地震信号s(t),子波w(t)和反射系数时间序列r(t)的频谱。
假设地震资料的有效频带为[flow,fhigh],则可以用频率采样间隔Δf在频带[flow,fhigh]上取M个不同的频点{fm=(m-1)×Δf+f1|m=1,2,…,M;M≥K}对谱方程进行离散,使得fm∈[f1,fM]且fm∈[f1,fM]⊆[flow,fhigh]。为充分利用地震资料部分谱的信息,通常频点选取需满足地震资料的主频f0∈[f1,fM],且频率采样间隔Δf满足Δf≤1/L,L为地震记录的有效时间长度。若子波已知,可消除子波的影响,建立反射系数时间序列的部分谱方程:

(4)
其中,ε为大于零的一个小数,确保子波谱W(f)在频率区间[f1,fM]出现零值时,依然可以通过谱除法得到反射系数有效的部分谱信息。由此,可将(4)式改写成矩阵形式:
(5)
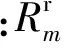
为了从(5)式中求出宽带的稀疏脉冲反射系数序列,由压缩感知理论[3-4],可建立反射系数在L1范数极小化意义下的最优化问题:
(6)

(7)
由于噪声的存在,需要加入正则化因子λ来压制噪声的影响,以保证反演结果的稳定[12],则(7)式的最小化问题可重写成:
(8)
由此,(8)式即为本文提出的基于压缩感知的稀疏脉冲反射系数谱反演方法的理论公式,可采用基追踪算法[9]稳定快速地求解,获得宽频带的稀疏脉冲反射系数离散序列α,即可利用(1)式生成反射系数时间序列r(t)。为方便后文讨论,简称该反演方法为CSSRI。

(9)

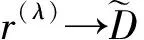
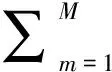
最后,利用CSSRI反演得到的反射系数时间序列r(t)褶积上宽频带的四参数Morlet子波[11],即可生成高分辨率地震记录。本文中取Morlet子波的实部,其函数解析表达式如下:
(10)
其频域表达式为:
(11)
其中,四参数向量γ={ωm,χ,u,φ},且ωm,χ,u和φ分别为Morlet子波平均角频率,时宽尺度因子,时间位置延迟量和初始相位。调节参数ωm,χ可以控制Morlet子波包络的时宽、旁瓣的大小、主频的高低、频带的宽度以及高(低)频振幅能量的大小。因此,适当地选取四参数,可以使得Morlet子波具有宽频带、弱旁瓣、保低频和压制高频噪声的特性,能够很好地模拟量化地震数据的频率和振幅能量,生成高品质的高分辨率地震记录。
2 应用实例
2.1 一维理论模型试验
针对一维稀疏脉冲反射系数模型,我们对比了CSSRI和最小平方反褶积[13]的试验效果,如图1所示。图1b所示的合成地震记录是有限带宽的雷克子波对宽频带的稀疏脉冲反射系数进行带限采样(滤波)后的结果,分辨率大大降低,难以直接识别出图1a所示的稀疏脉冲反射系数的准确位置和大小。合成地震记录采用的雷克子波峰值频率为25Hz,如图1c所示。利用本文提出的CSSRI方法,只需要地震资料的部分谱信息,即可消除地震子波带限采样的影响,重构出地下稀疏脉冲反射系数模型,如图1d和图1e所示,利用该结果可以准确地识别地下的反射地层情况。作为对比,传统的最小平方反褶积结果(图1f),虽然在一定程度上对子波进行了压缩,使分辨率得以提高,但并不能完全消除子波的影响,子波残留的旁瓣在薄层附近干涉形成虚假的波峰波谷,会给反射地层界面的解释带来一定的误导。
为测试噪声对CSSRI试验结果的影响,合成地震记录加入10%的随机高斯噪声后的试验结果如图2所示。由于合成地震记录加入了噪声,地震频谱信噪比占优的频带宽度会缩短,反演中可有效利用的频谱信息会减少,如图2a和图2b所示。例如,5Hz以下和60Hz以上的频谱,随机噪声(绿线)的能量开始占优,不能用于反演,这种带有误差的合成地震资料通常会引起反演结果的不稳定性。由于本文提出的CSSRI方法引入了L1正则化参数,可以在有效信号占优的频带内压制随机噪声对反演结果的影响,因此具有一定的鲁棒性。图2c为CSSRI反演的结果,尽管该反演结果不如图1e所示的无噪情况下反演的结果好,但重构的稀疏脉冲反射系数足以正确反映地下反射地层的位置和特征。作为对比,传统的最小平方反褶积的结果(如图2d所示)不仅对分辨率的提高不明显,还出现了虚假的谐波抖动和波峰(谷)。因此,对于稀疏脉冲反射系数模型,利用CSSRI可以从地震信号的部分谱信息中正确地反演出原始的稀疏反射系数模型,并且具有一定的抗噪性。
2.2 二维理论模型试验
为测试CSSRI刻画薄(互)层、透镜体边界以及地层尖灭位置的能力,我们基于Marmousi2模型的部分数据设计了具有薄层结构的二维稀疏地层反射系数模型,如图3a所示,相应的合成地震记录如图3b所示,采用的理论子波为峰值频率为30Hz的雷克子波。对比图3a和图3b可以看出,原始合成地震记录无法识别稀疏地层模型中的薄(互)层(图3中红色矩形框圈住的区域)、透镜体(图3中绿色椭圆框住的区域)和地层尖灭位置(图3 中蓝色虚线椭圆框住的区域)这些薄层结构。选取地震频带5~75Hz,利用CSSRI对合成地震记录进行反演,可以获得图3c所示的稀疏脉冲反射系数的高分辨率剖面。从图3c剖面中可以准确地识别出合成地震记录中无法识别的薄层结构,并且还保持了原始地层的横向连续性。作为对比,传统的最小平方反褶积的试验结果如图3d所示,尽管反射波同相轴有所变细,但分辨率提高不大,子波在薄层附近干涉依然较强,仍然无法准确识别稀疏地层模型中的薄层结构。这是因为最小平方反褶积作为一种线性滤波器并不能从本质上拓宽原始地震记录的频带宽度,反演出原始地震记录频带外缺失的频率成分,只能对原始地震记录自身频带内的频率成分(包括噪声)进行补偿。
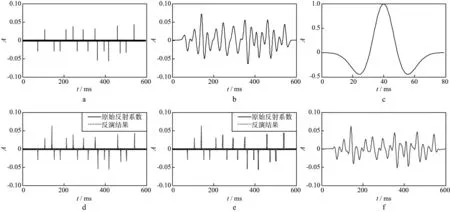
图1 无噪数据试验结果

图2 含随机噪声数据试验结果
合成地震记录加入5%的高斯随机噪声后,选取地震优势频带10~70Hz进行反演,反演结果如图3e所示。尽管CSSRI的反演结果在透镜体边界位置的反射系数振幅强度有所变弱,但依然可以识别出薄层结构。而含噪数据的最小平方反褶积结果的分辨率相对原始合成地震记录并没有明显提高,还对噪声进行了补偿,并且剖面出现了谐振噪声,如图3f所示。二维稀疏地层模型的试验结果表明,CSSRI可以从带限的合成地震记录中反演出宽带的稀疏脉冲反射系数,形成高分辨率的剖面,识别薄(互)层结构,并且能保持原始稀疏地层模型的横向连续性,正确地反映地下地层的接触关系,并且具有一定的抗噪性。但需要说明的是,当随机噪声强度不断增大,地震频谱的占优频带不断减小时,CSSRI的反演结果会逐渐丢失一些弱反射的薄层,但依然可以保持稀疏地层模型的整体地层格架特征。
2.3 实际资料应用
为了进一步分析CSSRI在地震信号高分辨率处理中的应用效果,将其应用于元坝地区某测线的实际地震资料,如图4所示。CSSRI反演过程中选取的地震占优(有效)频带为8~70Hz,采用的子波由基于测井数据约束下井旁地震道求取[14-15],若无井资料,可采用谱模拟法估计[16-17]。选取的Morlet子波参数为ωm=80π,σ=0.35,u=φ=0。对比图4a和图4b可见,CSSRI处理后的高分辨率剖面在整体上明显提高了原始地震剖面的分辨率,具有复波结构的地层接触关系更加清晰。为了进一步分析CSSRI高分辨率处理结果的应用效果,将图4a和图4b中红色虚线矩形框圈定的区域放大显示,如图4c和图4d所示。在图4c所示的原始剖面上无法识别的薄层(绿色虚线矩形框所示),复波的内幕地层特征(蓝色虚线矩形框),透镜状薄层弱反射(红色箭头所示)以及地层尖灭位置(绿色箭头所示),均在图4d所示的高分辨率剖面上有清晰的显示。这说明CSSRI能够从有限带宽的地震资料部分谱信息中,获取到能够揭示某些薄层结构的稀疏脉冲反射系数及其高分辨率地震剖面,为地震地层学的精细解释提供依据。此外,CSSRI处理得到的高分辨率地震剖面,尽管难以得到声波测井数据的分辨率(10-1米级),但也较好地保持了原始剖面的整体地层格架关系。这说明CSSRI处理得到的高分辨率剖面是忠实于原始地震资料的,并不是盲目地提高地震资料的分辨率,形成许多虚假的反射同相轴[18-19]。

图3 二维稀疏地层模型的试验结果
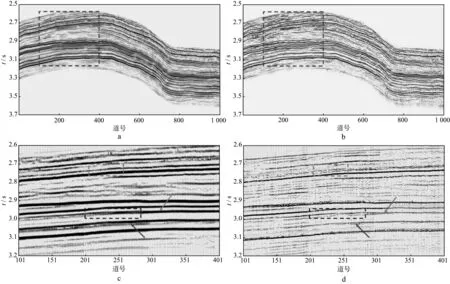
图4 实际地震记录及其CSSRI高分辨率处理剖面
3 讨论与结论
根据前文的介绍,利用地震资料的部分谱信息,在L1范数稀疏约束下,利用压缩感知基追踪算法可以稳健地获得宽频带的稀疏脉冲反射系数,突破香农采样定理的局限性,获得比原始地震资料频带宽度更宽的高分辨率地震剖面,识别原始地震资料中无法识别的薄层结构。从理论模型数据试验结果和实际资料的应用效果来看,相对于传统的最小平方线性反褶积,CSSRI的反演结果能明显提高原始地震资料的分辨率,生成的高分率剖面能够更加清晰地识别薄(互)层复波结构、透镜状砂体边界以及岩性尖灭位置,为复杂多变的沉积地层接触关系的精细地震解释提供依据。
但是,CSSRI作为一种反演技术,我们必须认真考虑两个问题。其一,反演结果的稳定性如何,由于CSSRI采用的基追踪算法具有良好的鲁棒性,理论模型试验和实际资料的应用效果已经证实了反演结果具有良好的稳定性。其二,是不是当地层厚度任意薄或者地震占优频带任意小时,该技术都能准确地反演出地下所有薄层的反射系数响应?显然,答案是否定的。根据压缩感知稀疏信号采样和重构理论,能否正确反演或重构地下所有地层的稀疏脉冲反射系数,除了受到反演算法本身正则化处理的影响外,还受到薄层厚度以及地震资料的占优带宽(或信噪比)的影响。当地震资料的品质较差,信噪比较低,占优频带较窄,而要识别的地层厚度又较薄时,CSSRI处理结果的质量也会随之降低,无法从复波结构中分离出所有的薄层弱响应;反之亦然。尽管如此,CSSRI反演得到的高分辨率剖面依然能够保持原始地震剖面的整体地层格架关系,忠实于原始地震资料。换句话说,CSSRI在进行地震资料高分辨率处理时,是在忠实于地震资料本身品质的前提下,充分挖掘地震资料的有效信息(如有效频带内的部分谱信息),最大程度地拓宽地震资料的有效频带宽度,获得相对可靠的高分辨率地震数据,而不是毫无节制的“无中生有”,生成虚假的高分辨率剖面。
[1] Widess M B.How thin is a thin bed?[J].Geophysics,1973,38(8):1176-1180
[2] Vetterli M.Sampling signals with finite rate of innovation[J].IEEE Transactions on Signal Processing,2002,50(9):1417- 1428
[3] Donoho D L,Elad M,Temlyakov V.Stable recovery of sparse overcomplete representations in the presence of noise:Stanford University[EB/OL].[2015-01-28] http:∥statweb.stanford.edu/~donoho/Reports/2004/StableSparse-Donoho-etal.pdf
[4] Donoho D L.Compressed sensing:Stanford University[EB/OL].[2015-01-28] http:∥statweb.stanford.edu/~donoho/Reports/2004/CompressedSensing091604.pdf
[5] Maravic I,Vetterli M.Sampling and reconstruction of signals with finite rate of innovation in the presence of noise[J].IEEE Transactions on Signal Processing,2005,53(8):2788-2805
[6] Debeye H W J,Van R P.Lp-norm deconvolution[J].Geophysical Prospecting,1990,38(2):381-403
[7] Mallat S,Zhang Z.Matching pursuit in a time-frequency dictionary[J].IEEE Transactions on Signal Processing,1993,41(12):3397-3415
[8] Pati Y C,Rezaiifar R,Krishnaprasad P S.Orthonormal matching pursuit:recursive function approximation with applications to wavelet decomposition[J].Proceedings of 27thAnnual Asilomar Conference on Signals,Systems and Computers,1993:40-44
[9] Chen S,Donoho D L,Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Journal of Scientific Computing,1999,20(1):33-61
[10] Gill P E,Murray W,Ponceleón D B,et al.Solving reduced KKT systems in barrier methods for linear and quadratic programming[R].Stanford University:Technical Report SOL 91-7,1991:1-24
[11] Morlet J,Arens G,Fourgeau E,et al.Wave propagation and sampling theory:part II,sampling theory and complex waves[J].Geophysics,1982b,47(1):222-236
[12] Tikhonov A N.Solution of incorrectly formulated problems and the regularization method[J].Soviet Mathematical Doklady,1963,4(5):1035-1038
[13] 渥.伊尔马滋.地震资料分析——地震资料处理、反演和解释(上册)[M].刘怀山译.北京:石油工业出版社,2006:122-216 Yilmaz Ö.Seismic data analysis:processing,inversion,and interpretation of seismic data[M].Liu H S,translator.Beijing:Petroleum Industry Press,2006:122-216
[14] Buland A,More H.Bayesian wavelet estimation from seismic and well data[J].Geophysics,2003,68(6):2000-2009
[15] 张广智,刘洪.印兴耀.井旁道地震子波精细提取方法[J].石油地球物理勘探,2005,40(2):158-162 Zhang G Z,Liu H,Yin X Y.Method for fine picking up seismic wavelet at uphole trace[J].Oil Geophysical Prospecting[J],2005,40(2):158-162
[16] Rose A L R,Ulrych T J.Processing via spectral modeling[J].Geophysics,1991,56(8):1244-1251
[17] 李鲲鹏,李衍达,张学工.基于谱模拟技术的混合相位地震子波估计方法[J].石油物探,2001,40(2):21-28 Li K P,Li Y D,Zhang X G,et al.The mixed-phase wavelet estimate method based on spectral modeling[J].Geophysical Prospecting for Petroleum,2001,40(2):21-28
[18] 李庆忠.走向精确勘探的道路——高分辨率地震勘探系统工程剖析[M].北京:石油工业出版社,1994:163-179 Li Q Z.The way to obtain a better resolution in seismic prospecting——a systematical analysis of high resolution seismic exploration[M].Beijing:Petroleum Industry Press,1994:163-179
[19] Wang J,Wang S,Yuan S,et al.Stochastic spectral inversion for sparse-spike reflectivity by presetting the number of non-zero spikes as a prior sparsity constraint[J].Journal of Geophysics and Engineering,2014,11(1):1-14
(编辑:朱文杰)
A spectral inversion method of sparse-spike reflection coefficients based on compressed sensing
Chen Zuqing,Wang Jingbo
(SinopecExplorationCompany,Chengdu610041,China)
Based on the theory of sparse sampling and signal reconstruction of compressed sensing,a spectral inversion method of sparse-spike reflection coefficients is proposed.Under the sparse-layer assumption,the sparse-spike broadband reflection coefficients can be inverted by the basis pursuit algorithm corresponding to theL1-norm constraint using the partial spectrums of seismic data.Through the convolution with a broadband four-parameter Morlet wavelet,the obtained sparse-spike reflection coefficients can be converted into high-resolution seismic data that can be applied to enhance the capacity of detecting thin beds.The inversion results on 1D synthetic data confirm the feasibility of reconstructing the sparse-spike reflectivity series accurately from the partial spectrums of seismic data.Furthermore,the testing on 2D sparse-layer synthetic data demonstrates that the inversion results can identify such thin-layer structures as the interfaces of thin interbed,the boundaries of lenticular sand body and the positions of stratigraphic pitchout,and preserve a good lateral continuity of the original sparse-layer model with a certain anti-noise capability.Finally,the actual application results shows that the obtained high-resolution seismic profile keeps the whole stratigraphic framework consistent with the original seismic data,distinguishes some thin-layer structures that cannot be identified by the original seismic data,and makes the subsurface stratigraphic contact relationship clearer,which can support the fine interpretation of seismic stratigraphy.
compressed sensing,sparse-spike reflection coefficients,spectral inversion,L1norm,basis pursuit algorithm,Morlet wavelet,high resolution
2015-01-29;改回日期:2015-03-25。
陈祖庆(1968—),男,高级工程师,主要从事石油物探技术研究工作。
王静波(1985—),男,博士,工程师,主要从事地震资料处理、反演方法研究工作。
国家科技重大专项“海相碳酸盐岩储层预测与流体识别技术研究”专题(2011ZX05005-005-005)资助。
P631
A
1000-1441(2015)04-0459-08
10.3969/j.issn.1000-1441.2015.04.013
