三维高斯射线束观测系统照明及优化方法研究
2015-06-27殷厚成
殷厚成,邓 飞
(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.成都理工大学信息科学与技术学院,四川成都610059)
三维高斯射线束观测系统照明及优化方法研究
殷厚成1,邓 飞2
(1.中国石油化工股份有限公司石油物探技术研究院,江苏南京211103;2.成都理工大学信息科学与技术学院,四川成都610059)
基于模型的观测系统照明分析技术在复杂地区的观测系统设计中起着非常重要的作用,但随着野外勘探复杂程度的增加,三维地质模型也更加复杂,常用的射线方法在精度上已经不能很好地满足实际生产的需求,波动方程类方法则由于计算效率较低在实际使用中存在很大局限性。提出了一种基于高斯射线束的双向照明方法,给出了方法的实现步骤。该方法将波场分解到具有一定宽度的射线束上实现波场的模拟和延拓,通过检波点射线坐标反向变换,根据互易性原理实现观测系统的双向照明,不仅大幅提高了计算效率,而且有效改善了照明的精度。根据高斯射线束照明结果分析和统计炮点对各目的层面元的双向照明贡献,优选对低能量目的层区域贡献大的炮点附近进行补炮,从而实现观测系统的局部优化。采用一个三维地质模型验证了高斯射线束双向照明算法的合理性和正确性。
高斯射线束;射线束照明;双向照明;观测系统设计;观测系统优化
传统的地震勘探基于水平叠加理论,其前提是假定地下为水平层状介质;但随着我国油气勘探的不断深入和发展,探区的地质目标日益复杂,基于水平层状假设的常规观测系统设计不能满足勘探需求,尤其是在起伏地表和复杂构造地区。以地质模型为基础的照明分析[1]技术是一项对地震波能量分布进行定量分析的技术。通过波场数值模拟照明分析,可以研究震源及检波器对目标地质体的照明及接收能量,根据观测系统照明能量分布,有效指导观测系统设计。
目前常用的观测系统照明方法主要包括射线法和波动方程法两类。射线法[2-3]因效率较高很早就被应用于观测系统设计,其中两点射线追踪[4]可用于计算观测系统对目的层面元的覆盖次数,以覆盖次数近似替代能量来进行照明分析。该方法具有高效、灵活的特点,但存在射线阴影区、焦散区等问题,而且以覆盖次数近似替代能量也存在一定的精度问题。波动方程类方法包括单程波[5]和全程波[6]两种,与射线法相比,这类方法通过直接求解波动方程进行波场延拓,解决了多波至以及由速度变化引起的聚焦或焦散效应问题,数值计算精度高。但是波动方程类方法对硬件设备要求较高,计算效率低,因而在实际应用中受到较多限制。
射线束方法是一类介于射线和波动方程之间的照明分析方法,高斯射线束[7-9]是射线束方法的代表,它将波场分解到具有一定宽度的射线束上来实现波场的模拟和延拓,不仅具有运动学特征,而且具有动力学特征,可以精确计算中心射线附近波场的振幅和相位,在一定程度上解决了射线的盲区、焦散问题,并能够自然地实现多波至。然而,由于高斯射线束自身的特点,直接将高斯射线束方法套用到已有的单程波照明框架上无法将检波点记录整体反向延拓,而逐检波点延拓的效率很低,无法实现高效的双向照明计算。为了提高高斯射线束的效率,本文在高斯射线束波场延拓的基础上,通过检波点射线坐标反向变换,根据互易性原理实现了快速的高斯射线束双向照明。
1 高斯射线束观测系统照明及优化方法
观测系统照明实质上就是利用数值模拟方法研究观测系统在指定地质模型上的照明能量强度分布,因此现有的地震波场数值模拟方法均可以应用于照明分析。射线方法是一种最早被人们应用于地震波场数值模拟的经典方法,该方法根据地质模型的速度变化追踪地震波在地下介质中的运动轨迹及其在地质界面上的反射和透射变化,算法简单且效率较高,但其主要反映地震波的运动学特征,不能很好地表现动力学特点。
传统的射线方法是将波场分解到单一的射线上来实现波场数值模拟的,获取高精度的合成记录需要大量精确的射线。利用试射法进行的两点射线追踪需要耗费大量的时间,而且由于射线的局限性很难有效地解决射线盲区、多波至等问题。分析认为,传统射线法的这些缺陷是由于将波场分解到完全理想的高频射线上造成的,如果将波场分解到一定高频范围内的射线能量带上,就可以从根本上改进射线法的效果。高斯射线束方法就是一种利用“胖射线”思想进行波场数值模拟的方法,地下介质或检波点处的波场不再由单一的一条射线决定,而是由多条射线(束)叠加获得。射线束方法的特性决定了它可以在很大程度上克服传统射线方法的缺点,因此具有很高的计算效率和较高的精度。
1.1 三维高斯射线束方法原理
高斯射线束方法最初由Cerveny等[7-9]在20世纪80年代提出并用于地震记录正演,后来又被Hill[10-11]用于偏移成像。在高斯射线束数值模拟中,高斯射线束是波动方程集中于射线附近的高频渐近解[7],它可以被看作是一条从震源出发以射线为中心的能量管,射线束的振幅以偏离中心射线的距离呈指数衰减,因类似于高斯分布而得名,而地下介质中某处或检波点处的波场则由一定范围内的多条高斯射线(束)叠加形成。完整的高斯射线束正演算法包括运动学射线追踪、动力学射线追踪和波场叠加三个步骤[12]:通过运动学射线追踪获得中心射线轨迹和中心射线能量的变化;通过动力学射线追踪沿中心射线计算高斯射线束的动力学参数,确定高斯射线束的振幅衰减和波前曲率;波场叠加则用于对计算点有贡献的高斯射线束叠加并形成最终的波场记录。
高斯射线束建立在射线坐标系下,三维情况下的射线坐标系如图1所示,S为中心射线,S附近有一点P。过P点作垂直于射线的平面,与射线交于P′点,P′到起点S0的射线路径长度为s。n,m为P点垂直于射线的平面内的二维笛卡尔坐标,P点相对于中心射线S的射线坐标记为(s,n,m)。从图1可以看出,射线坐标系的基矢量由遵循右手坐标系的3个正交的单位矢量et,en,em构成。其中et为射线的单位正切矢量,而en和em垂直于射线,并且保持射线坐标系是正则的。

图1 三维射线坐标系
设在射线起点S0处已知射线出射方向为et0,它与z轴夹角为α,其xoy平面投影与x轴夹角为β,那么et0可表示为:
(1)
由于en,em和et是用于确定射线坐标系的单位向量,它们互相垂直,因此可以选择
(2)
当射线在变速介质中前进时,et会发生变化,en,em也要随之变化,它们满足如下微分方程:
(3)

在上述射线坐标系下,三维高斯射线束可以表示为:
(4)

(5)
(5)式即为三维高斯射线束动力学方程组,式中v(s)是速度关于局部坐标en,em的2×2二阶偏导数矩阵,矩阵的各个元素表示为:
(6)
复值动力学矩阵P(s)/Q(s)决定了高斯射线束的特征,其实部特征值Re[P(s)/Q(s)]决定了高斯射线束在射线上的相前曲率,而其虚部则决定了高斯射线束在垂直于射线截面上的振幅分布,并且三维高斯射线束的半宽度矩阵可以表示为:
(7)
L(s)的两个特征值分别决定了在垂直于射线的平面上呈椭圆分布的振幅长、短轴。
1.2 基于高斯射线束的双向照明
在震源点处将波场分解到一系列的高斯射线束中,利用高斯射线束公式(4),可以将波场延拓到模型的任意位置处,计算地下介质或检波点处的地震波场并统计该处的照明能量。然而单纯通过目的层的入射或者检波点的接收照明能量并不能直观地判断观测系统的优劣,观测系统照明需要综合考虑震源和检波器排列的综合效应,原因就像文献[13]中形象比喻的那样:“在黑暗中用手电筒照亮一个物体,视力好的人可以看到该物体,但即使物体被照得再亮,也无法被盲人看见”。一方面,即使某目的层入射能量再高,若无法被观测系统接收,那么之后的资料处理也无法使该目的层成像;另一方面,检波器排列接收的能量再高,若没有接收到有效目的层的能量,那么成像结果也是无效的。
评判观测系统优劣的照明能量应能综合考虑震源和检波器排列,而双向照明能量正是这样一种能量,它是经过目的层反射且被检波点接收的能量。很明显,这是可以用于目的层成像的有效照明能量。双向照明最早由Xie等在文献[5]中提出,朱金平等在文献[13]中给出了一种效率较高的单程波双向照明方法DUC-DC。该方法分为两步:①首先从震源点向下延拓波场至模型底部,然后再将反射波场向上延拓回地表,得到检波点处的波场,这一步相当于正演;②将检波点处的波场再次向下延拓至地下介质,获得双向照明强度。
高斯射线束双向照明的计算,可以采用与单程波方法类似的框架,模仿DUC-DC方法进行。首先利用高斯射线束进行正演模拟计算,获得各检波点处的正演记录;然后逐检波点使用高斯射线束将波场进行反向延拓,得到地下介质的照明强度。与单程波方法相比不同之处在于,单程波方法的反向延拓可以将检波点处的记录作为整体向下延拓,而高斯射线束并不能将多个检波点处的记录作为整体一次性向下延拓,必须逐检波点进行。假设观测系统中有Ns个震源,每个震源平均影响排列中的Ng个检波点,那么采用DUC-DC方法的双向照明框架,需要进行Ns×(1+Ng)次高斯射线束延拓,计算效率很低。
为了提高高斯射线束双向照明的效率,应避免从检波点处进行反向延拓。双向照明的目的是求出被检波点接收的面元反射能量,因此,如果能够充分利用正演时的射线束直接求出双向照明能量,则将大幅提高计算效率。为此,考查一条从震源出发的射线束Bi,如图2所示,该射线束经反射面反射回到地表被检波点G所接收。设反射面上有一点C,求C点关于射线束Bi对检波点G的双向照明能量,即求出射线束Bi经C点反射被检波点G所接收的能量。
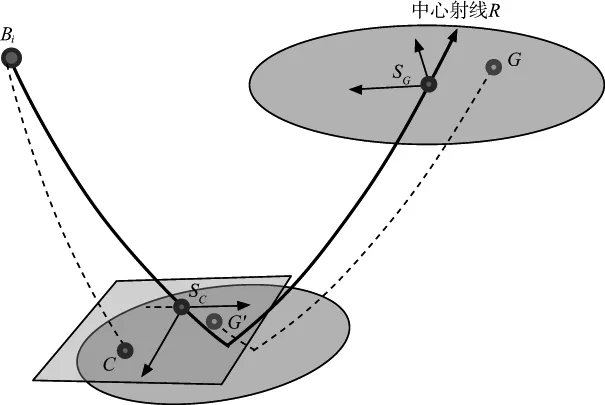
图2 高斯射线束双向照明计算
对于给定的射线束Bi,首先根据高斯射线束公式(4)求出检波器G点相对于中心射线R的射线坐标(sG,nG,mG),并求出G的振幅A(G)和照明能量。根据射线束原理,G点接收的能量是由反射面上射线束有效范围内的反射点共同决定的。由于C点的射线坐标为(sC,nC,mC),而G点的射线坐标是(sG,nG,mG),为了求出反射面上C点对G点的贡献,可以沿中心射线将G点从sG位置反向延拓至sC位置,记为G′,求出G′点及其射线坐标(sC,nG′,mG′)。进行反向延拓时G′点的振幅等于G点处振幅A(G),如果此时将G′点作为中心射线位置,可求出C点相对于G′点的平面内二维笛卡尔坐标:
(8)
将其代入(4)式即可求出G′点对C点的振幅贡献A(C)。根据互易性原理,A(C)即为C点对检波点G的双向照明振幅。对上述算法思路进行整理,可以得到高斯射线束单炮双向照明的算法步骤:
1) 确定射线角度范围和射线角度间隔;
2) 遍历所有的射线角度,重复步骤3)至9);
3) 按照射线出射角度进行运动学和动力学射线追踪,确定中心射线路径R及动力学参数矩阵P,Q;
4) 根据中心射线R,计算反射面元点相对于中心射线的射线坐标,选取高斯射线束半宽度范围内的面元点,作为计算的有效面元点,记为集合{C};
5) 根据中心射线R在地表的出射位置,计算检波点的射线坐标,选取半宽度范围内的检波点,作为有效检波点,记为集合{G};
6) 遍历有效检波点集合{G},重复步骤7)至9);
7) 根据检波点Gi的射线坐标,按照公式(4)计算检波点振幅A(Gi);
8) 遍历有效面元点集合{C},重复步骤9);
9) 将检波点Gi的射线坐标反向延拓到面元点Cj所在的射线坐标系下,得到(SCj,nGi′,mGi′),利用公式(8)和公式(4)求得双向照明振幅A(i,j)和能量E(i,j),并将求得的照明能量累计到面元Cj上。
使用上述算法在正演计算后无需逐检波点进行反向延拓获取双向照明强度,只需在射线束正演的过程中增加检波点射线坐标反向延拓和面元点能量计算的工作。由于正演过程本身就要计算和记录射线坐标系的变换矩阵,因此求检波点的反向延拓坐标仅需要乘以变换的逆矩阵即可。使用该方法每炮仅需要做1次射线束延拓运算,Ns个震源仅需进行Ns次射线束延拓运算,计算效率相对于之前的逐检波点延拓提高了Ns×Ng倍。
1.3 基于照明结果的观测系统优化
高斯射线束照明具有很高的计算效率,能够完成上万甚至数十万炮的双向照明计算,因此可以利用高斯射线束进行观测系统论证。首先建立待勘探工区的三维地质模型,利用常规观测系统设计软件设计几个备选观测系统,然后利用高斯射线束对不同观测系统下的地质模型进行双向照明计算,挑选出目的层照明均匀、能量较高的观测系统作为优选观测系统。
由于地表起伏或地下构造复杂,优选出的观测系统对目的层的照明仍然可能存在不均匀和能量较低的暗区,通常需要补充一些炮点以得到优化的观测系统,增加低能量区的照明强度。问题是如何确定合理的加炮区域,使得增设的炮点对待加强的低能量目的层区域产生最大化贡献。为此,可以在照明计算时记录炮点对各目的层面元的双向照明贡献,当选择出低能量区域后,查询并统计出地表炮点对选定区域的贡献,优先选择贡献大的炮点附近作为补炮的候选区域。在候选区域补充炮点之后再次计算并分析目的层双向照明能量,如果达到预期效果则输出优化后的观测系统,否则按照上述方法补充更多的炮点。
2 模型算例分析
为了验证高斯射线束双向照明算法的合理性和正确性,采用一个三维地质模型进行了试算(图3)。模型在X,Y,Z三个方向上的尺寸分别为32000,18000,15800m,包含6个层位,4个断层。各层速度由上至下分别为:5625,6100,6300,4800,5400,6000m/s。
给定2个备选观测系统Ⅰ和Ⅱ。观测系统Ⅰ的基本参数如下:20线,每线300道,道间距40m,线间距200m,共11500炮。观测系统Ⅱ的基本参数如下:28线,每线288道,道间距40m,线间距240m,共10692炮。测试用计算机为联想T440p,CPU为i7-4700MQ/2.4GHz,内存4.0GB,64位Win7操作系统。选择模型第3层为目的层进行高斯射线束双向照明计算,每炮的单线程平均计算时间为1978ms,使用4线程同时计算,观测系统Ⅰ照明共耗时87min,观测系统Ⅱ照明共耗时89min。
图4是观测系统Ⅱ中(13950m,9750m)处炮点的双向照明效果,可以看到,由于地表起伏和断层割裂,目的层的照明并没有呈现出圆形,主要照明能量被分割为明显的两块。图5对比了观测系统Ⅰ和观测系统Ⅱ的双向照明效果,可以看到观测系统Ⅱ的照明能量、覆盖范围和均匀度均高于观测系统Ⅰ,因此选择观测系统Ⅱ进行进一步优化。

图3 三维地质模型
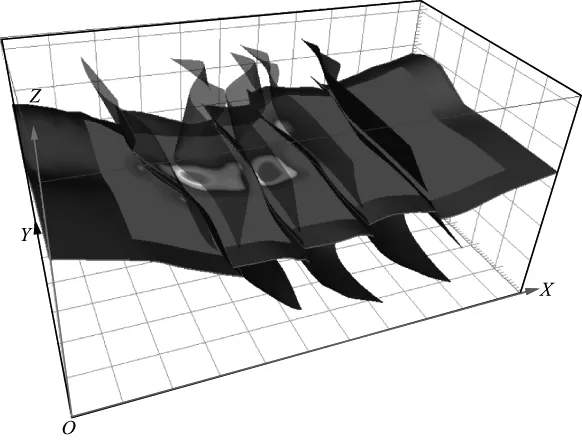
图4 单炮双向照明效果
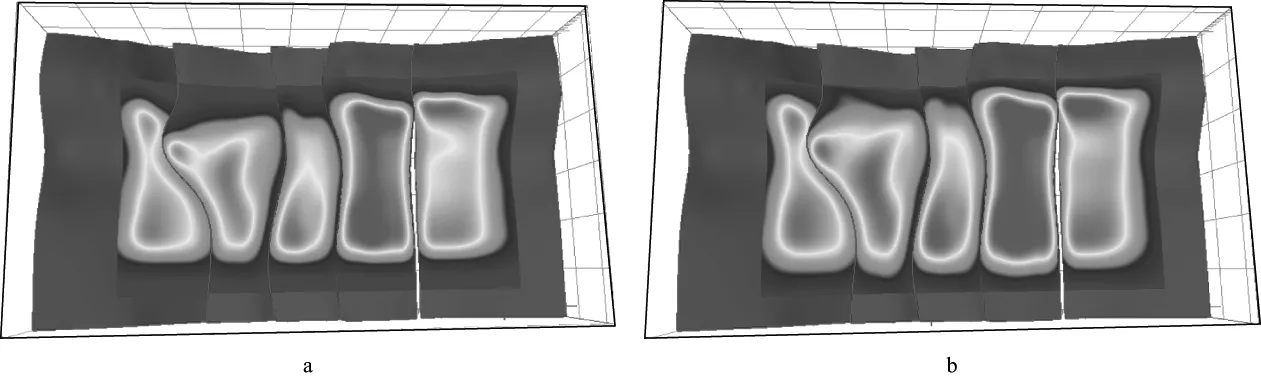
图5 观测系统双向照明结果对比
选择目的层上的低能量区域,如图6a所示;统计炮点对选中区域的照明贡献并绘制在地表上,如图6b所示。按照贡献大小在原炮点附近半炮距位置处增设100个新炮点,增加新炮点后的照明效果如图6c所示,可以看到低能量区域的照明效果得到了明显改善。应用相同方法对观测系统Ⅱ继续进行优化,补入650炮点后的最终照明效果如图6d 所示,与图5b相比照明效果有显著提高。

图6 观测系统Ⅱ优化
3 结束语
照明分析是观测系统设计与优化的重要手段,基于高斯射线束的双向照明方法通过对原有射线束正演方法进行扩展,仅需要增加少量工作即可完成双向照明计算,既能保持射线法高效、灵活的特点,又能提高射线法计算的精度,照明能量强弱过渡自然,效果近似于波动方程类方法,能够很好地应用于复杂三维地质模型的照明分析。
利用高斯射线束照明结果可以实现观测系统优选。通过对照明结果的统计和分析,可以自动确定目的层局部低能量区,从而确定优势补炮区域。通过在推荐区域补炮,可以显著提高低能量区的照明效果。
由于高斯射线束双向照明方法具有很高的计算效率,因此能够在普通微机上完成大规模三维观测系统的照明计算和分析,满足野外观测系统设计的实际需求。
[1] Berkhout A J,Ongkiehong L,Volker A W F,et al.Comprehensive assessment of seismic acquisition geometries by focal beams,part Ⅰ:theoretical considerations[J].Geophysics,2001,66(3):911-917
[2] Bear G,Lu C P,Lu R,et al.The construction of subsurface illumination and amplitude maps via ray tracing[J].The Leading Edge,2000,19(7):726-728
[3] Hoffmann J.Illumination,resolution,and image quality of PP-and PS-waves for survey planning[J].The Leading Edge,2001,20(9):1008-1014
[4] 徐涛,徐果明,高尔根,等.三维复杂介质的块状建模和试射射线追踪[J].地球物理学报,2004,47(6):1118-1126 Xu T,Xu G M,Gao E G,et al.Block modeling and shooting ray tracing in complex 3D media[J].Chinese Journal of Geophysics,2004,47(6):1118-1126
[5] Xie X B,Jin S W,Wu R S.Wave-equation-based seismic illumination analysis[J].Geophysics,2006,71(5):169-177
[6] 陈生昌,马在田,吴如山.波动方程双程地下方向照明分析[J].同济大学学报(自然科学版),2007,35(5):682-684 Chen S C,Ma Z T,Wu R S.Two-way subsurface directional illumination analysis by wave equation[J].Journal of Tongji University(Natural Science),2007,35(5):682-684
[7] Cerveny V,Psencik I.Gaussian beams and paraxial ray approximation in three-dimensional elastic in homogeneous media[J].Geophysical Journal Royal Astronomical Society,1983,53(1):1-15
[8] Cerveny V.Gaussian beams synthetic seismograms[J].Journal of Geophysics,1985,58(1):44-72
[9] Cerveny V.Ray synthetic seismograms for complextwo-dimensional and three-dimensional structures[J].Journal of Geophysics,1985,58(1):2-26
[10] Hill N R.Gaussian beam migration[J].Geophysics,1990,55(11):1416-1428
[11] Hill N R.Prestack Gaussian-beam depth migration[J].Geophysics,2001,66(4):1240-1250
[12] 邓飞,刘超颖.三维射线快速追踪及高斯射线束正演[J].石油地球物理勘探,2009,44(2):158-165 Deng F,Liu C Y.3D rapid ray-tracing and Gaussian ray-beam forward simulation[J].Oil Geophysical Prospecting,2009,44(2):158-165
[13] 朱金平,董良国.地震波双向照明的概念及计算方法[J].地球物理学报,2011,54(11):2933-2942 Zhu J P,Dong L G.The concept and calculation method of bi-directional seismic illumination[J].Chinese Journal of Geophysics,2011,54(11):2933-2942
(编辑:戴春秋)
Research on seismic acquisition geometry illumination and its optimization based on 3D Gaussian beam
Yin Houcheng1,Deng Fei2
(1.SinopecGeophysicalResearchInstitute,Nanjing211103,China;2.CollegeofInformationScienceandTechnology,ChengduUniversityofTechnology,Chengdu610059,China)
The seismic geometry illumination technology based on geological model plays an important role on seismic exploration in complex area.However,since the field exploration becomes more and more complicated,3-D geologic model becomes more complex and the conventional ray method isn’t able to meet the need of actual production.On the other hand,the wave equation method has many limitations in practical application because of low efficiency.Using Gaussian beams to carry out wavefield forward simulation and continuation,Gaussian beam bi-directional illumination method not only keeps the high-efficiency and flexibility but also overcomes some shortcomings of conventional ray method,effectively solves the problem of rapid illumination on complex 3-D geologic model.According to Gaussian beam illumination result we can choose the best seismic geometry,and realize local optimization based on analysis and statistics of the result.
Gaussian beam,ray beam illumination,bi-directional illumination,seismic geometry design,seismic geometry optimization
2015-02-27;改回日期:2015-05-15。
殷厚成(1963—),男,高级工程师,长期从事地震采集技术攻关与研究工作。
国家科技重大专项“煤层气地震采集和处理技术”项目(2011ZX05035-002)资助。
P631
A
1000-1441(2015)04-0376-06
10.3969/j.issn.1000-1441.2015.04.002
