基于奇异值分解的时变子波提取准确性评价方法

王蓉蓉,戴永寿,李 闯,张漫漫,张 鹏

(1.中国石油大学(华东)信息与控制工程学院,山东青岛266580;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580)

基于奇异值分解的时变子波提取准确性评价方法

王蓉蓉1,戴永寿1,李 闯2,张漫漫1,张 鹏1

(1.中国石油大学(华东)信息与控制工程学院,山东青岛266580;2.中国石油大学(华东)地球科学与技术学院,山东青岛266580)

子波提取准确性的评价在地震数据处理中占有重要地位，但是传统的评价准则受噪声影响较大。为此，提出一种基于奇异值分解(SVD)的时变子波提取准确性评价方法，考虑非平稳地震记录的子波提取准确性评价方法中Parsimony准则、丰度准则和绝对峰度准则对噪声环境的承受能力较强，选用Parsimony准则与奇异值分解技术结合，构造了一种抗噪/容噪能力更强的时变子波提取准确性评价准则SVD_P。将SVD_P准则、Parsimony准则和丰度准则同时应用于仿真数据和实际资料处理，对比分析了时频域时变子波提取方法与自适应分段时变子波提取方法的准确性，结果表明：SVD_P准则、Parsimony准则和丰度准则都能对两类子波提取方法进行正确的评价，时频域子波提取法提取子波的准确性高于自适应分段法提取的子波，但是SVD_P准则评价的结果相对误差最小，评价精度最高。

子波提取;准确性;评价准则;奇异值分解

地震子波提取是地震反演和地震解释的基础，其准确性直接影响后续处理的结果[1-2]。由于子波在传播过程中受地层吸收作用的影响导致高频成分的缺失和相位特征的畸变，因此地震记录具有非平稳性[3-4]。针对非平稳地震记录中子波提取准确性的判别，目前并无成熟有效的评价方法，因此，非平稳地震记录中时变子波提取准确性评价方法的研究对提高地震资料分辨率具有重要意义。

在非平稳地震记录中提取时变子波，现有的比较有效的两种思路是：①将非平稳地震记录划分为多个时窗后，每段记录视为近似平稳地震记录提取子波；②将非平稳地震记录变换到时频域，逐点提取时变子波。直接通过波形、能量或其它地震子波自身的属性，都不能对子波提取精度有一个精确的评估[5]，目前较为有效的方法是通过非平稳地震记录反褶积得到反射系数序列，结合现有的评价准则对反射系数序列进行评价，进而间接评价子波提取准确性。

目前主要评价准则有Parsimony准则[6]、丰度准则[7]、绝对峰度准则[8]、相似系数准则[9]和基于互信息率的判别准则[10]。但这些评价准则对改变其信号时域特性的噪声较敏感，在有噪声污染的信号中应用这些准则进行子波提取准确性评价效果不佳。为了解决这个问题，本文提出一种基于奇异值分解的子波提取准确性评价方法，结合反褶积结果的主奇异值成分和Parsimony准则，构造一种抗噪/容噪能力较强的SVD_P准则，利用模型分析和实际地震资料对方法进行了验证。

1 基于奇异值分解的子波提取准确性评价方法

1.1 非平稳地震记录中时变子波提取

1.1.1 时频域时变子波提取

针对非平稳地震记录,基于时频域的时变子波提取方法如下:首先应用改进的广义S变换将非平稳地震记录变换到时频域,在时频谱的点谱上拟合子波;然后在频率域采用谱模拟法获取每个时刻的子波振幅谱，采用基于高阶累积量[11-12]的双谱法预估计子波相位谱,结合局部相似度[13]逐点拾取时变子波相位谱,进而实现非平稳地震记录混合相位时变子波的提取。

改进的广义S变换的窗函数表达式为[14]：

(1)

式中:q,p为大于0的调节因子。从公式(1)中可以看出,窗函数的宽度与频率呈正比例变化,即在低频处可获得较高的时间分辨率,在高频处可获得较高的频率分辨率,符合地震记录动态衰减的特性。利用该方法对地震记录进行时频分析,可获得更高的时频分辨率和很好的时频聚焦,能够有效地分辨出地震资料中频率成分的变化。利用该方法还可进行无能量损失的反变换,准确重构时间域地震信号。

1.1.2 自适应分段子波提取

对非平稳地震记录分段处理的核心思想是将地震记录划分为多个时窗并将每段记录视为平稳地震记录，然后对每段记录提取子波。假设在同一层段中反射界面上的地震子波是时不变的,则可认为每个层段产生的地震记录满足Robinson模型[15],随着地层深度的增加,不同层段中的子波是时变的。

本文采用高静怀等[16]所提出的自适应分子分解法对非平稳地震记录进行分段,通过谱拟合得到每段地震记录的子波振幅谱,结合基于高阶累积量的双谱重构法提取的相位谱[17-18],完成混合相位子波提取。

1.2 含噪反褶积建模及反褶积处理

1.2.1 含噪反褶积建模

地震记录含有噪声的情况下,可以用Robinson褶积模型[19]表示为：

(2)

其中,r(n)为反射系数序列,w(n)为地震子波,v(n)为随机干扰噪声。上述信号应当满足如下假设:

1) 反射系数序列为独立同分布过程;

2) 环境噪声v(n)为随机干扰噪声,且与r(n)统计独立,因此与x(n)也相互独立。

(3)

由公式(3)可以看出,由于噪声的影响,反褶积结果并不仅仅为原始反射系数序列,还含有噪声与逆子波的成分，反褶积结果的性质已经偏离原始反射系数序列,若采用传统方法对此结果进行子波提取准确性评价,通常得不到准确的结果。因此,寻找一种抗噪能力较强的评价准则对子波提取准确性评价至关重要。

1.2.2 反褶积处理

由于反褶积是检验提取子波准确性的重要工具,其结果直接影响子波评价的准确性,因此,对适合于非平稳地震记录的反褶积方法的研究是子波提取准确性评价方法的重要环节。

现有的确定性反褶积方法已经十分成熟,如最小二乘反褶积、最小熵反褶积[20]、稀疏脉冲反褶积[21]、谱稀疏贝叶斯学习反射系数反演[22]、多分辨率地震信号反褶积[23]、基追踪反演[24]等。由于ARMA模型描述下的子波在时域表现为无限长脉冲响应序列,时域反褶积处理不可避免地要对子波进行截断，为了减少截断误差对反演过程的影响,在提取时变子波后,我们选择谱除法在频率域做反褶积处理。

将Robinson褶积模型进行傅里叶变换可得：

(4)

其中,X(ejω),W(ejω)和R(ejω)分别为地震记录、地震子波和反射系数序列的频域表示。则反射系数序列的估计可表示为：

(5)

1.3 基于奇异值分解的评价方法

SVD滤波[25-26]是通过利用地震记录的相关性优化提取信息来达到波场分离与去噪目的的[27-28]。沈鸿雁等[29]指出,将地震记录特征值或奇异值作为正交基,通过矩阵分解与变换将其转换到新的坐标系,利用信号能量与噪声的可分性将较大奇异值成分重构,即可实现对随机噪声的消除,增强相干能量。

设地震记录为x,采样点数为N,x=[x1,x2,…,xn],由此构成的分解矩阵Dm可表示为:

(6)

式中:m为矩阵重构的维数；n为时间延迟量,为每维记录个数。各变量之间的关系可由(m-1)×τ+n=N确定。时间延迟量的计算采用单道地震记录自相关归一化方法求取,可表示为[30]：

(7)

对分解矩阵Dm进行奇异值分解,其奇异值由两部分组成,即：

(8)

式中:SDM是分解矩阵Dm对应的奇异值;SD为有效信号对应的奇异值;SV为随机干扰对应的奇异值。

采取保留地震信号对应的奇异值，其它奇异值置零的方法对矩阵进行重构,从而得到去除随机噪声后的地震信号。将该方法与传统的子波提取评价准则结合，可构造有效去除随机噪声的评价准则。对非平稳地震记录中子波提取准确性评价方法的研究表明,Parsimony准则、丰度准则和绝对峰度准则对噪声环境的承受能力强。因此本文将Parsimony准则与奇异值分解技术结合,构造一种抗噪/容噪能力强的时变子波提取准确性评价准则。

王友新等[31]指出,Parsimony的意思是“节约”或“吝啬”,表示地震记录经过该准则处理后可以使结构更简单[32],即：

(9)

其中,xi为反褶积结果,满足n>2。

新构造的评价准则称之为SVD_P准则,公式如下:

(10)

式中:xSVD表示对反褶积结果进行奇异值分解并取主奇异值重构反射系数序列,满足n>2。当只有一个尖脉冲时,PSVD(x)=0。由于该准则采用了xi的对数形式,因此可以使强反射和弱反射都能够对重构结果产生一定的影响。

将SVD_P准则与Parsimony准则和丰度准则进行对比以验证SVD_P准则的优越性。丰度准则公式为:

(11)

式中:xi为反褶积结果。该方差模准则的最大值代表一个满足非高斯性质的概率密度分布函数的峰值,其值越大,概率密度分布形状越尖锐。

2 实验分析

为了验证本文提出的基于奇异值分解的时变子波提取准确性评价准则SVD_P的有效性,本文采用自回归滑动平均模型(ARMA)描述地震子波并合成地震记录,通过对称映射ARMA模型零极点的方式构造因果性及相位性不同的地震子波并进行反褶积处理。采用基于奇异值分解的时变子波提取准确性评价准则对反褶积结果进行评价,辨识出真实的反射系数序列,从而判断出真实的地震子波。

采用Margrave等[33]提出的具有明确吸收效应的非平稳褶积模型构造非平稳地震记录,公式为：

s(t)=w(f)αQ(u,f)r(u)exp[2πif(t-u)]dfdu

(12)

式中:s(t)表示地震记录;w(f)为地震子波;r(u)

为反射系数序列;αQ(u,f)为衰减因子,可以表示为:

(13)

式中：Q为大地滤波因子。本实验中采用混合因果、混合相位子波作为真实子波,如图1a所示。图1b 为本文选用的反射系数序列,该反射系数序列满足独立同分布IID及Bernoulli-Gaussian分布,采样间隔为1ms,长度为1000ms,其与地震子波褶积合成的地震记录如图1c所示,构造的非平稳地震记录如图1d所示。

2.1 方法的有效性验证

2.1.1 未加入噪声时评价准则的准确性

以图1a所示混合相位子波为真实子波,采用时域对称映射ARMA模型零极点的方式构造出一系列因果性及相位性不同的地震子波[34],其时域波形如图2a所示(第12道为真实子波)。应用构造出的不同子波对合成的非平稳地震记录(图1d)进行反射系数序列反演,通过谱除法在频域进行反褶积处理,最后将频域反褶积结果映射到时域进行比较。16个不同相位谱子波反褶积处理后的结果如图2b所示,其中第12道为真实子波反演结果。

图1 仿真实验分析

图2 构造的16道子波(a)及反射系数序列反演结果(b)

由图2b可以看出,仅真实子波能够完全恢复真实的反射系数序列,其余子波反演结果均不满足真实反射系数序列的稀疏性质。应用SVD_P准则、Parsimony准则及丰度准则对图2b所示反射系数序列进行评价,确定出真实或准确的反射系数序列,结果如图3所示。

由图3可知,SVD_P准则及Parsimony准则的最小值对应真实反射系数,而丰度准则最大值对应真实反射系数。可见在未加入噪声的情况下,各种评价准则均能识别出真实反射系数序列,进而识别出真实地震子波(第12道)。

2.1.2 噪声对评价准则的影响

为了得到适用于实际地震资料,对噪声环境承受能力较强的评价准则,我们将合成的非平稳地震记录(图1d)加入不同信噪比的高斯白噪声,采用构造的16道地震子波(图2a)进行反褶积处理,并用SVD_P准则、Parsimony准则及丰度准则对16道反褶积结果进行对比判别。3种评价准则对噪声环境的承受能力如表1所示。

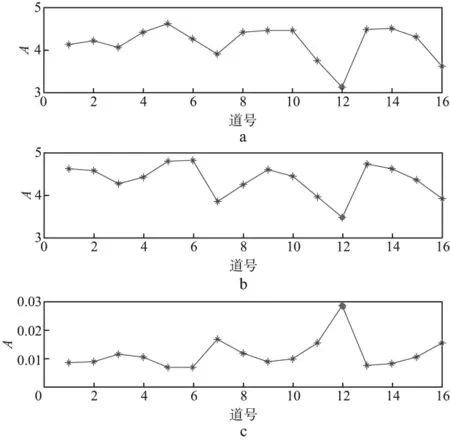
图3 不同评价准则评价结果

表1 噪声对评价准则的影响

注:“√”表示可准确判别;“×”表示无法准确判别。

由表1实验结果可以看出,本文所提出的基于奇异值分解的子波提取准确性评价准则对所有噪声强度是有效的,具有良好的抗噪/容噪能力,优于Parsimony准则和丰度准则。

2.2 时变子波的提取

2.2.1 时频域时变子波提取

在时频域点谱上采用谱模拟法提取子波振幅谱,结合双谱法及局部相似度重构子波相位谱,提取图1d中非平稳地震记录的时变子波。图4分别为100,500,520,900ms时原始子波与提取的时变子波时域波形对比图。

由图4可知:①在t=100ms时,时频域提取的子波时域波形与理论值比较吻合,随着时间的增加,拟合出的子波振幅逐渐减少,能够反映出子波在传播过程中的动态衰减特性,说明了子波提取的正确性;②在500ms和520ms处,由于层位相距较近,子波相互叠加难以识别,但这两个点仍有较好的子波提取结果,说明该方法能够较准确地提取出每一反射点处的子波。

2.2.2 基于自适应分段提取时变子波

采用自适应分子分解法[16]对图1d所示非平稳地震记录自适应分段,如图5所示。图5a表示非平稳地震记录,红色曲线表示希尔伯特变换得到的振幅包络,绿色“*”表示包络峰值。取图5a中两个相邻峰值的中点位置作为每个初始分子窗的终点位置;将位于相邻终点内的原子窗累加,得到初始分子窗,如图5b所示;采用自适应分子分解法得到自适应分子窗(图5c),将地震记录分为8段,从左至右分别为1,2,…,8。

将图5c划分的每段地震记录进行谱拟合,再进行傅里叶反变换后得到每段的子波振幅，采用基于高阶累积量的双谱重构法提取子波相位,每段子波提取结果如图6所示。在图6中,蓝色实线为每段地震记录估计得到的子波,红色虚线为实际子波。

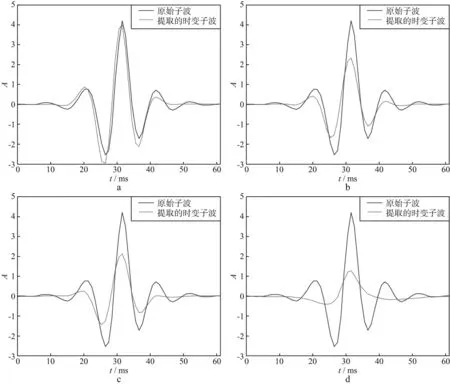
图4 原始子波与提取的时变子波波形对比

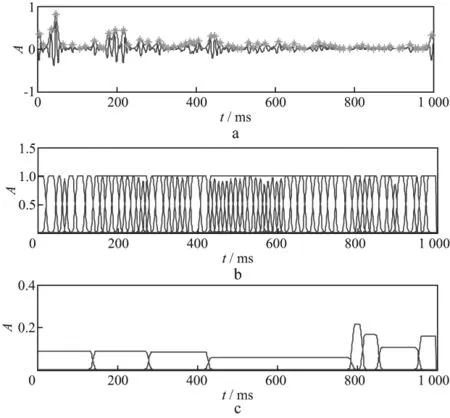
图5 自适应分子分解法分段

由图6可知:①第1～2段估计得到的子波振幅和相位与实际子波基本一致,说明地震波在浅层传播时受到的地层吸收作用较小;②随着深度的增加,地层吸收作用越来越明显,第3～8段估计得到的子波时域波形变宽、频带变窄、振幅衰减,但仍能保持子波的基本形态。子波估计的结果真实反映了地震波在地下的传播规律,从侧面证实了基于自适应分段处理的子波提取的正确性。

图6 自适应分子分解分段法提取的每段子波

2.3 反射系数序列反演

根据以上两种方法估计得到子波后,通过公式(5) 对非平稳地震记录做反褶积处理。时频域时变子波提取后通过逐点谱除得到反褶积结果;分段处理方法对各段地震记录提取子波后,对每段记录分别做反褶积处理。图7a 为原始反射系数序列,图7b为时频域反褶积结果;图7c为时频域反褶积结果的误差;图7d为分段后反褶积结果;图7e 为分段后反褶积结果的误差。

由图7可知:①分段后反褶积结果中噪声较弱,可以分辨大部分层位,部分薄层及反射系数较小的层位(箭头所示位置)难以分辨;②时频域反褶积结果中基本没有噪声,且层位清晰,更接近真实反射系数;③两种反褶积结果与真实反射系数的差均较小,说明两种方法估计得到的子波都能反演出较准确的反射系数。

2.4 应用评价准则对反褶积结果的评价

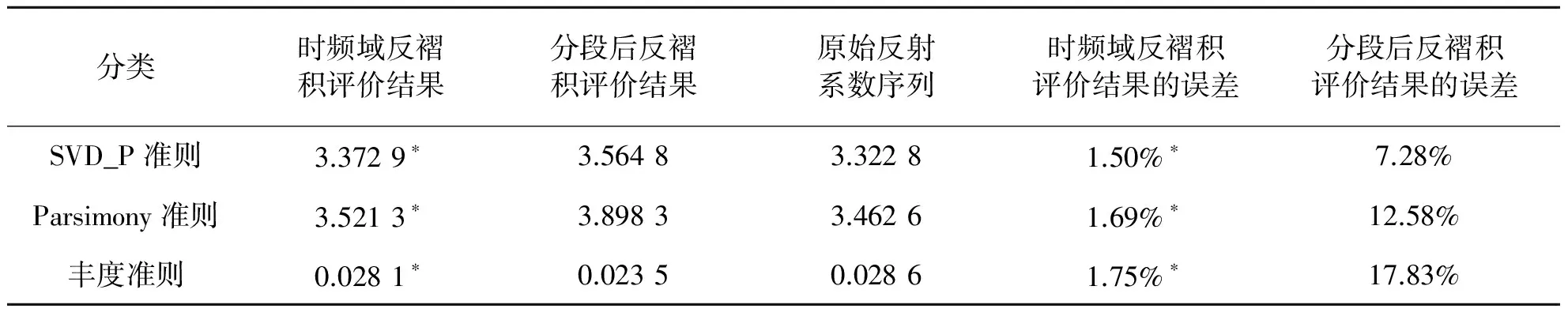
对图7中两种反褶积结果及真实反射系数分别应用SVD_P准则、Parsimony准则及丰度准则进行评价,结果如表2所示。从2.1节的讨论中可知,反褶积结果越接近真实反射系数,SVD_P准则和Parsimony准则的值越小,丰度准则的值越大。据此判断,表2中带“*”标志的数据为最佳结果。

由表2可以看出,时频域反褶积得到的反射系数序列更加接近真实值,这与2.3节反褶积对比的结果是一致的。因此,时频域时变子波提取法提取子波的准确性高于自适应分段提取的子波。由表2还可以看出,虽然SVD_P准则、Parsimony准则及丰度准则都能对两类子波提取方法进行正确的评价,但是SVD_P准则评价的结果相对误差最小。

图7 反褶积结果分析

表2 不同评价准则对两类反演结果的评价及其相对误差

分类时频域反褶积评价结果分段后反褶积评价结果原始反射系数序列时频域反褶积评价结果的误差分段后反褶积评价结果的误差SVD＿P准则3．3729∗3．56483．32281．50%∗7．28%Parsimony准则3．5213∗3．89833．46261．69%∗12．58%丰度准则0．0281∗0．02350．02861．75%∗17．83%

3 实际地震数据应用效果分析

图8a为某探区实际二维地震剖面,图8b为第189道地震记录。分别应用时频域时变子波提取法和自适应分段子波提取方法提取地震子波,结果如图9所示。

由图9可见:自适应分段子波估计和时频域时变子波估计两种方法提取的子波形态相似,都能反映出子波在传播过程中的动态衰减特性。为了判断两种子波提取方法的准确性,根据图9中的子波分别对地震记录做反褶积,得到估计的反射系数序列,如图10所示。分别应用SVD_P准则、Parsimony准则和丰度准则对两种反褶积结果和测井得到的反射系数序列(图10c)进行了评价,结果如表3所示。

根据2.1节讨论的结果判断,表3中带“*”标志的评价结果为最佳结果，因此时频域时变子波提取法提取的子波准确性高于自适应分段提取的子波。由表3还可以判断,虽然SVD_P准则、Parsimony准则及丰度准则都能对两类子波提取方法进行正确的评价,但是SVD_P准则评价的结果相对误差最小,评价精度最高。

图8 实际地震剖面(a)与第189道地震记录(b)

图9 实际数据子波提取结果

图10 实际数据反褶积结果分析

表3 不同评价准则对两类反演结果的评价及其相对误差

分类时频域反褶积评价结果分段后反褶积评价结果原始反射系数序列时频域反褶积评价结果的误差分段后反褶积评价结果的误差SVD＿P准则4．2756∗4．43174．02166．31%∗10．20%Parsimony准则4．5352∗4．59274．13269．74%∗11．13%丰度准则0．0171∗0．01690．019311．40%∗12．43%

4 结论

本文研究表明，通过谱除法在频域进行反褶积处理、提取反褶积结果的主奇异值成分并结合Parsimony准则进行子波提取准确性评价的方法(SVD_P准则)是有效且可行的。与Parsimony准则和丰度准则相比，SVD_P准则对随机干扰噪声的承受能力更强，更适用于实际地震资料子波估计的准确性评价。

[1] 袁三一,王尚旭.子波相位不准对反演结果的影响[J].应用地球物理,2011,8(1):48-59 Yuan S Y,Wang S X.Influence of inaccurate wavelet phase estimation on seismic inversion[J].Applied Geophysics,2011,8(1):48-59

[2] 王蓉蓉,戴永寿,张亚南,等.非平稳地震记录中时变子波提取方法研究[J].地球物理学进展,2015,30(2):700-708 Wang R R,Dai Y S,Zhang Y N,et al.Time-varying wavelet extraction methods in non-stationary seismogram[J].Progress in Geophysics,2015,30(2):700-708

[3] 戴永寿,王俊岭,王伟伟,等.基于高阶累积量ARMA模型线性非线性结合的地震子波提取方法研究[J].地球物理学报,2008,51(6):1851-1859 Dai Y S,Wang J L,Wang W W,et al.Seismic wavelet extraction via cumulant based ARMA model approach with linear and nonlinear combination[J].Chinese Journal of Geophysics,2008,51(6):1851-1859

[4] 刘喜武,刘洪,李幼铭,等.局域波分解及其在地震信号时频分析中的应用[J].地球物理学进展,2007,22(2):365-375 Liu X W,Liu H,Li Y M,et al.Local waves decomposition and its applications to seismic signal time-frequency analysis[J].Progress in Geophysics,2007,22(2):365-375

[5] 陈健,戴永寿,张亚南,等.基于高阶统计量的地震子波提取方法评价[J].石油地球物理勘探,2013,48(3):497-503 Chen J,Dai Y S,Zhang Y N,et al.Summary of the evaluation approaches for seismic wavelet pick-up based on higher order statistics [J].Oil Geophysical Prospecting,2013,48(3):497-503

[6] 李振春,王希萍,韩文功.地震数据处理中的相位校正技术综述[J].地球物理学进展,2008,23(3):768-774 Li Z C,Wang X P,Han W G.Review of phase correction in seismic data processing[J].Progress in Geophysics,2008,23(3):768-774

[7] White R E.Maximum kurtosis phase correction[J].Geophysical Journal,1988,95(2):371-389

[8] 何同林,郑鹏,刘郁林,等.基于峰度准则与判决引导的非线性盲解卷积[J].电子科技大学学报,2007,36(2):186-189 He T L,Zheng P,Liu Y L,et al.Nonlinear blind deconvolution based on kurtosis criterion and decision directed algorithm[J].Journal of University of Electronic Science and Technology of China,2007,36(2):186-189

[9] 姚逢昌.振幅谱补偿和相位校正[J].石油物探,1990,29(3):46-58 Yao F C.Amplitude spectra compensation and phase correction[J].Geophysical Prospecting for Petroleum,1990,29(3):46-58

[10] Pham D T.Generalized mutual information approach to multichannel blind deconvolution[J].Signal Processing,2007,87(9):2045-2060

[11] 戴永寿,郑德玲,魏磊,等.高阶统计量地震子波估计建模[J].石油地球物理勘探,2006,41(5):514-518 Dai Y S,Zheng D L,Wei L,et al.Primary research on modeling for wavelet estimation via high-order cumulants[J].Oil Geophysical Prospecting,2006,41(5):514-518

[12] 唐斌,尹成.基于高阶统计的非最小相位地震子波恢复[J].地球物理学报,2001,44(3):404-410 Tang B,Yin C.Non-minimum phase seismic wavelet reconstruction based on higher order statistics[J].Chinese Journal of Geophysics,2001,44(3):404-410

[13] 刘玉金,李振春,郭恺.基于局部相似度的非稳态相位校正方法[J].石油地球物理勘探,2012,47(6):887-893 Liu Y J,Li Z C,Guo K.Non-stationary phase correction based on local similarity[J].Oil Geophysical Prospecting,2012,47(6):887-893

[14] 齐春艳,李彦鹏,彭继新,等.一种改进的广义S变换[J].石油地球物理勘探,2010,45(2):215-218 Qi C Y,Li Y P,Peng J X,et al.An improved generalized S-transform[J].Oil Geophysical Prospecting,2010,45(2):215-218

[15] Ziolkowski A.Why don’t we measure seismic signatures? [J].Geophysics,1991,56(2):190-210

[16] 高静怀,汪玲玲,赵伟.基于反射地震记录变子波模型提高地震记录分辨率[J].地球物理学报,2009,52(5):1289-1300 Gao J H,Wang L L,Zhao W.Enhancing resolution of seismic traces based on the changing wavelet model of the seismogram[J].Chinese Journal of Geophysics,2009,52(5):1289-1300

[17] 张亚南,戴永寿,王少水,等.高效 ARMA 模型高分辨率地震子波提取方法[J].石油地球物理勘探,2011,46(5):686-694 Zhang Y N,Dai Y S,Wang S S,et al.High resolution wavelet estimation by ARMA modeling[J].Oil Geophysical Prospecting,2011,46(5):686-694

[18] Wang R R,Dai Y S,Li C,et al.A time-varying mixed-phase wavelet extraction and evaluation method based on adaptive segmentation[J].Electronic Journal of Geotechnical Engineering,2015,20(6):1403-1418

[19] Robinson E A.Predictive decomposition of time series with application to seismic exploration[J].Geophysics,1967,32(3):418-484

[20] Wiggins R.Minimum entropy deconvolution[J].Geoexploration,1978,16(5):21-35

[21] Sacchi M D.Re-weighting strategies in seismic deconvolution[J].Geophysical Journal International,1997,12(9):651-656

[22] Yuan S Y,Wang S X.Spectral sparse Bayesian learning reflectivity inversion[J].Geophysical Prospecting,2013,61(4):735-746

[23] 章珂,李衍达,刘贵忠,等.多分辨率地震信号反褶积[J].地球物理学报,1999,42(4):529-535 Zhang K,Li Y D,Liu G Z,et al.Multiresolution seismic signal deconvolution[J].Chinese Journal of Geophysics,1999,42(4):529-535

[24] Zhang R,Castagna J.Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J].Geophysics,2011,76(6):147-158

[25] Oropeza V E,Sacchi M D.Multifrequency singular spectrum analysis[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009,3193-3197

[26] Li C,Huang J P,Li Z C,et al.Simultaneous de-noising and regularization method for 3D field data based on the MSSA[J].CPS/SEG International Geophysical Conference,2014,296-299

[27] Yuan S Y,Wang S X.A local f-x Cadzow method for noise reduction of seismic data obtained in complex formations[J].Petroleum Science,2011,8(3):269-277

[28] Oropeza V E,Sacchi M D.A randomized SVD for multichannel singular spectrum analysis (MSSA) noise attenuation[J].Expanded Abstracts of 80thAnnual Internat SEG Mtg,2010,1989-1992

[29] 沈鸿雁,李庆春.奇异值分解 (SVD) 实现地震波场分离与去噪新思路[J].地球物理学进展,2010,25(1):225-230 Shen H Y,Li Q C.New idea for seismic wave filed separation and denoising by singular value decomposition(SVD)[J].Progress in Geophysics,2010,25(1):225-230

[30] 胡永泉,尹成,潘树林,等.基于单道奇异值分解的微地震资料去噪方法[J].石油天然气学报,2013,35(4):64-69 Hu Y Q,Yin C,Pan S L,et al.Denoising method for microseismic data based on single-channel SVD[J].Journal of Oil and Gas Technology,2013,35(4):64-69

[31] 王有新,周兴元.最小熵反褶积和集约化准则[J].石油地球物理勘探,1993,28(6):678-684 Wang Y X,Zhou X Y.Minimum entropy deconvelution and parsimonious criterion[J].Oil Geophysical Prospecting,1993,28(6):678-684

[32] 李大卫,尹成,赵维坤,等.基于相位扫描的地震子波提取方法研究[J].西南石油大学学报,2007,29(3):17-19 Li D W,Yin C,Zhao W K,et al.Seismic wavelet extraction based on phase scan[J].Journal of Southwest Petroleum University,2007,29(3):17-19

[33] Margrave G F,Lamoureux M P,Henley D C.Gabor deconvolution:estimating reflectivity by nonstationary deconvolution of seismic data[J].Geophysics,2011,76(3):W15-W30

[34] 张亚南,戴永寿,陈健,等.用对称映射ARMA模型的零极点研究子波相位对反射系数序列反演的影响[J].地球物理学报,2013,56(6):2043-2054 Zhang Y N,Dai Y S,Chen J,et al.The research on the influence of wavelet phase on the inversion results of reflection coefficient sequences by using the ARMA model of symmetrical mapping pole-zeros[J].Chinese Journal of Geophysics,2013,56(6):2043-2054

(编辑：戴春秋)

An evaluation criterion on the accuracy of time-varying wavelet extraction based on singular value decomposition

Wang Rongrong1,Dai Yongshou1,Li Chuang2,Zhang Manman1,Zhang Peng1

(1.CollegeofInformationandControlEngineering,ChinaUniversityofPetroleum,Qingdao266580,China;2.SchoolofGeosciences,ChinaUniversityofPetroleum,Qingdao266580,China)

The accuracy evaluation of time-varying wavelet extraction plays an important role in seismic data processing.However,the conditional evaluation criterion is influenced seriously by noise.Therefore,we propose a time-varying wavelet accuracy criterion based on singular value decomposition (SVD).Since the Parsimony criterion,Kurtosis criterion and Absolute kurtosis criterion have good tolerability to noisy environment among the existing evaluation criteria for the non-stationary seismic wavelet extraction accuracy,the Parsimony criterion and SVD technology are combined to construct a SVD_P criterion which has better noise-tolerant ability; and the spectrum division is employed as the deconvolution method.The Parsimony criterion,Kurtosis criterion and SVD_P criterion are applied to the simulation experiment and field data processing to compare the precision of time-frequency domain time-varying wavelet extraction method and adaptive segmentation time-varying wavelet extraction method.The results show that all three criteria could provide valid evaluation of these two wavelet extraction method while the time-frequency domain wavelet extraction method is more accurate than the adaptive segmentation method.Additionally,the evaluation result of SVD_P criterion owns smallest error and highest evaluation precision.

wavelet extraction,accuracy,evaluation criterion,singular value decomposition

2015-01-13;改回日期：2015-04-24。

王蓉蓉(1990—),女,硕士在读,主要从事地震信号处理方法研究工作。

戴永寿(1963—),男,教授,博士生导师,主要从事地震信号处理方法研究工作。

国家自然科学基金项目(40974072)和中国石油大学(华东)研究生创新工程资助项目(YCX2015050)联合资助。

P631

A

1000-1441(2015)05-0531-10

10.3969/j.issn.1000-1441.2015.05.006