向量空间分解理论探究

张鑫浩

（镇江高等专科学校；丹阳师范学院，江苏丹阳 212300）

向量空间分解理论探究

张鑫浩

（镇江高等专科学校；丹阳师范学院，江苏丹阳 212300）

文章首先在复数域下，引出了简化版的Cayley-Hamilton定理，在此基础上根据根子空间的概念，先讨论了根子空间的循环分解理论；再讨论根子空间的直和，即空间的准素分解理论；最后介绍了如何用复数域上的空间分解理论来处理实数域上的空间分解．

向量空间；根子空间；空间分解理论

目前向量空间上的空间分解理论大多是从特征值到方阵的对角化，然后从Cayley-Hamilton定理得到空间的准素分解理论（初步的空间分解理论），再引入λ矩阵，讲了不变因子、初等因子//Jordan标准型等概念，最后再讲精细的空间分解理论．本文没有在一般的数域上讨论空间分解，而是先在复数域上讨论根子空间分解理论，再讨论准素分解理论，最后在实数域上讨论空间的分解理论．这对于其他数域也有一定的借鉴作用．

1 在复数域上的空间分解理论

1.1 复数域下的Cayley-Hamilton定理

由于在复数域上任一线性变换（算子）A，在某组基e1，e2，…，en下有上三角矩阵[1]68

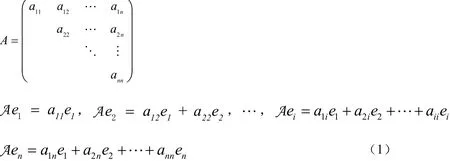
为了表述的方便，我们记Vi=（e1,e2,…,ei）i=1,2,…,n

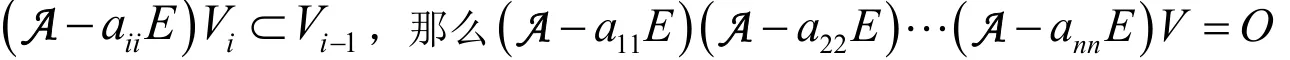
1.2 空间分解的初步探究

1.2.1 在上述矩阵中，若a11，a22，…，ann均不相同，易见矩阵A有n个不同的特征根，则线性变换A可对角化．即线性变换（算子）A，在某组基下对应与如下形状的矩阵

1.2.2 我们考虑重根的情况，将与a11相同的特征值均记为λ1（t重根）．

我们将1λV称为1λ的根子空间[2]．

1.3 对根子空间Vλ1的空间分解

对应于第一种类型的向量构成的空间，我们称之为属于特征值λ1的特征子空间．

对于第二种类型的向量，我们讨论

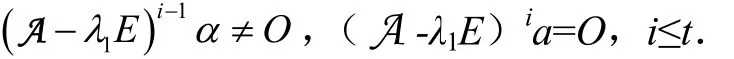
1.3.2 循环子空间的扩充与极小变换

在上述过程中，我们是对属于1λV的向量不断的施加线性变换（A-λ1E）来作出循环子空间的，现在反过来，对于属于1λV中的向量ε1i的，考虑方程组（A-λ1E）X=ε1i在1λV中是否有解．若存在β∈1λV，使得（A-λ1E）β=ε1i，则L（ε11，ε12，…，ε1i，β）是有向量β生成的循环子空间，且L（ε11，ε12，…，ε1i）继续这样的过程，直至找不到更大的循环子空间为止．

若由向量ε1i生成的循环子空间已经不能再扩充时，我们将重点放在这样的向量上．为了叙述方便引入新的名称，称（A-λ1E）i是向量ε1i在线性变换（A-λ1E）下的极小变换（算子），此时有：（1）在中无解，（2）

1.3.3 由相同极小变换的向量生成的循环空间

用（A-λ1E）i-1分别作用在等式两边，得到

若η1与ε11线性无关，则ki=k1i=0，并由此推出k1=k11=…=ki=k1i=0，因此

注意到η1与ε11经过一次线性变换（A-λ1E）均为零向量，η1与ε11均为线性变换A的特征向量，所以有：两个特征向量线性无关，则分别含此特征向量的具有相同极小变换的向量生成的循环子空间交空．

1.3.4 由不同极小变换的向量生成的循环空间

将（A-λ1E）s-1分别作用在等式两边，得到若η11与ε11线性无关，则并由此推出

即两个特征向量线性无关，则分别含此特征向量的具有不同极小变换的循环子空间交空．

1.3.5 由特征向量作出循环子空间

设属于特征值λ1的线性无关的特征向量有m个，分别用表示．首先我们找出含ε11的循环子空间．解线性方程（A-λ1E）a=ε11，得到ε12，再由（A-λ1E）a=ε12，得到ε13依此类推就得到含有ε11的循环子空间，记为Vλ1（ε11）．但在此过程中，解并不唯一．例如解（A-λ1E）a=ε11时，不仅（A-λ1E）ε12=ε11，

我们希望解得的12ε具有唯一性，于是限定因此，这样的是唯一的．若存在112W∈′ε，使得可得此时这与1W是子空间相矛盾．所以必有依次类推可得该循环子空间的唯一性．

1.3.6 根子空间的循环分解

我们将包含上述特征向量的循环子空间用Vλ1表示．

下证：Vλ1=Vλ1（ε11）⊕Vλ1（ε21）⊕…⊕Vλ1（εm1）

证明：由上述讨论知，Vλ1（ε11），Vλ1（ε21），…，Vλ1（εm1）两两交空．

下面用数学归纳法证明：

对任意一向量α∈Vλ1，α∈Vλ1（ε11）⊕Vλ1（ε21）⊕…⊕Vλ1（εm1）．

（1）当n=1时，因为（A-λ1E）a=O，结论显然成立．

另一方面，存在

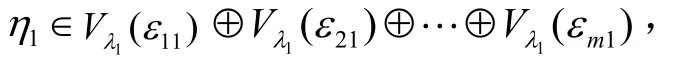
两式相减得（A-λ1E）k（a-η1）=0，记a-η1=ξ1，因为（A-λ1E）kξ=0，所以所以证毕．

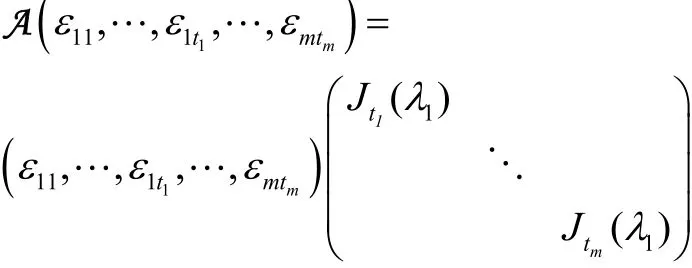
11=t有

1.4 根子空间1λV的维数

由于1λV的维数就是齐次线性方程组解空间的维数，取某组特定的基，使得线性变换在这组基下对应于上三角矩阵，对应于分块矩阵其中11A是t行t列的主对角线元素为0的上三角行列式，22A是上三角行列式，则对应于矩阵易知该矩阵的秩为n-t，所以解空间的秩为t，1λV的维数也是t．

1.5 不同的根子空间交空

为了表述方便，下面的论述令t=l1，同理若λ2是A的l2重根，记同样具有Vλ1的形式，且两者交空．否则令α=Vλ1∩Vλ2，因互素，所以存在u（x），v（x）使得

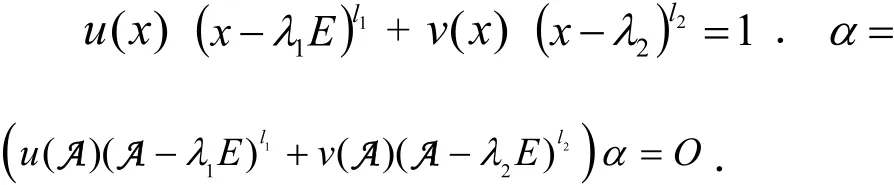
1.6 空间的准素分解理论

存在u1（x），u2（x），…，us（x）使得

所以，命题得证．

于是我们仿照1λV中的做法，分别取中的一组基，合在一起．得到

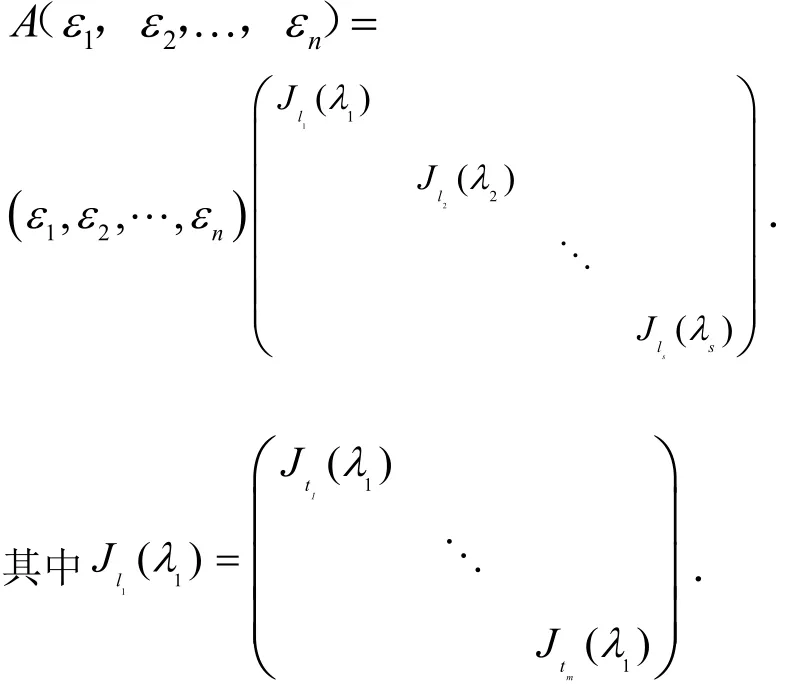
2 在实数域上的空间分解

特征多项式f（x）为一次或二次因式的乘积，写成标准分解式为

对于一次因式，A在某组基下对应的矩阵同上所述为J（λ）型．

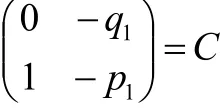
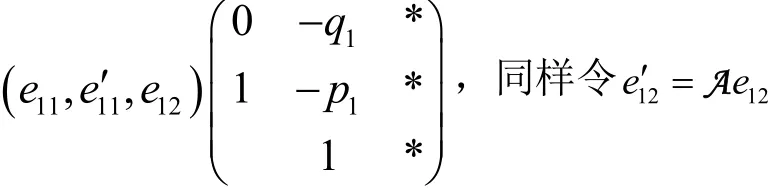
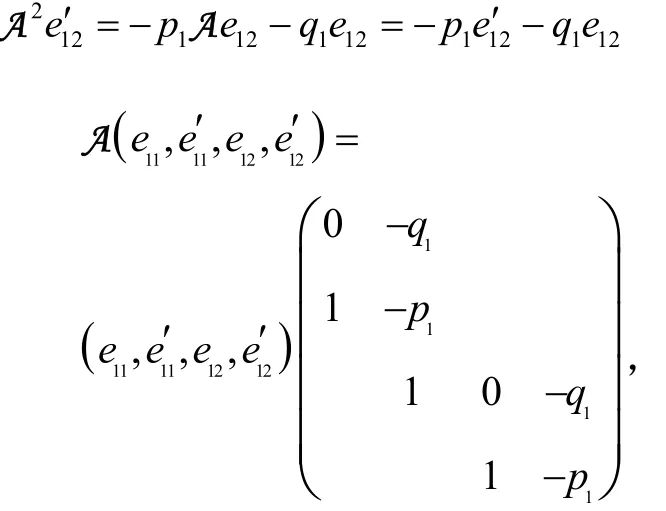
若（A2+p1A+q1E）α11≠O，则依次类推，最终必为

用这个方法就可以作出线性变换A在向量空间V在实数域上的一个分解．

[1][俄罗斯]柯斯特利金.代数学引论[M].牛凤文，译.北京：高等教育出版社，2008.

[2]张贤科，许甫华.高等代数学[M]北京：清华大学出版社，2004.

[3]丘维声.高等代数[M].北京：高等教育出版社，2010.

（责任编辑：于开红）

An Exploration of the Theory of Vector Space Decomposition

ZHNAG Xinhao (Zhenjiang College, Danyang Normal College, Danyang Jiangsu 212300)

Under the complex domain, this article first introduces the simplified version of the Cayley-Hamilton theorem, and on this basis, according to the concept of root space, it discusses the cyclic decomposition theory of the root space, and the inner direct sum of root space, or the primary decomposition theory of space. Finally it explores how to use space on complex domain decomposition theory to deal with real space on domain decomposition.

vector space; root space; space decomposition theory

G642

A

1009-8135（2015）03-0025-05

2015-01-30

张鑫浩（1975-），男，江苏丹阳人，讲师，主要研究数学教育．