一道几何命题射影解法的启示

赵临龙

（安康学院数学与应用数学研究所，陕西安康 725000）

一道几何命题射影解法的启示

赵临龙

（安康学院数学与应用数学研究所，陕西安康 725000）

利用射影几何的极点与极线关系，给出一道几何命题的射影解法，揭示命题的内在联系，从中获得射影几何学习的两点启示：注重《高等几何》的学习研究及其作用的发挥.

欧氏几何；射影几何；极点；极线

2008年2期的《中等数学》在“本期问题”中，给出高220题[1]：

如图1．从⊙O外一点P引⊙O的两条切线PA、PB，切点为A、B，再从点P引⊙O的两条割线PCD、PEF，与⊙O交于点C、D、E、F，弦CF、DE交于点G.求证：A、G、B三点共线．

本题有着深刻的射影几何背景．现利用射影几何作以探讨.

1 射影几何解法

2.1 极点与极线的概念

如图2．过点M引二次曲线Γ的直线MAB交Γ于A、B两点，若直线MAB上一点N满足：NA/NB = MA / MB，则点N轨迹（直线l）为点M关于Γ的极线，点M为Γ关于极线l的极点．

特例：当点M在Γ上，则过M与Γ相切的直线为点M关于Γ的极线l.

图1

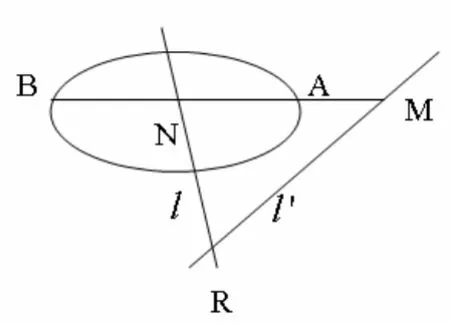
图2

2.2 极点与极线的性质

定理1[2]若点M关于二次曲线Γ的极线为l，则l上一点N关于二次曲线Γ的极线'l必过点M.

推论1 极线l的点列N与过极点M的线束'l构成一一对应.

推论2 两极点M、N对应极线分别是l和'l，则l和'l的交点R的极线为直线MN.

定理2[2]如图1．二次曲线内的完全四边形CDEF的三双对边分别交于：CF × DE = G，CE ×DF = Q，CD × EF = P，则ΔPQG为自极三角形（Δ的每一个顶点关于对边构成二次曲线的极点和极线的关系）.

2.3 命题的证明

如图1. 由于ΔPQG是二次曲线内接完全四边形CDEF的自极三角形，则极点G的极线是PQ，极点Q的极线是PG.

又直线PA、PB分别切二次曲线于点为A、B，则极点A、B的极线分别是PA切线和PB切线．

此时，由于4条极线PQ、PG；PA、PB都交于点P，则它们分别对应的4个极点G、Q；A、B共线．

即命题获得证明.

推论3 如图1．从二次曲线外一点P引它的两条切线PA、PB，切点为A、B，再从点P引它的两条割线PCD、PEF，与二次曲线交于点C、D、E、F，弦CF、DE交于点G，弦CD、EF交于点Q．则Q、A、G、B四点共线.

显然，在推论中，再过点Q作二次曲线外一点Q引它的两条切线QA1、QB1，切点为A1、B1，则P、A1、G、B1四点也共线．

由此，给出一个几何命题的作图问题．

问题 如何利用直尺作出过二次曲线外一点P作它的切线？

作法：过点P引二次曲线的两条割线PCD、PEF，与二次曲线交于点C、D、E、F，连接弦CF、DE交于点G，连接CE、DF交于点Q，再连接QG分别交二次曲线于点T、T1．于是PT、PT1为所求的切线．

2 射影几何解法的启示

2.1 注重《高等几何》的学习和研究

射影几何解法不仅给出了问题的求解，更重要的是揭示了问题的本质，自然能给出“新”的结论．因此，教师应该注重《高等几何》的学习和研究，从更深层次把握问题的实质．如在《高等几何》中，数学神童帕斯卡于1964年给出的结论：

帕斯卡定理[3]对于任意一个内接于非退化的二次曲线的六边形，则它的三双对边的交点共线．

我们利用射影几何的“对偶原理”（将一个几何命题中的“线”换成“点”，并将“点”换成“线”，所得命题与原命题成对偶命题），则得结论：

布里安桑定理[3]对于任意一个外切于非退化的二次曲线的六边形，则它的三对对顶的连线交于一点．

该定理于1806年由布里安桑给出（当时还没有“对偶原理”理论）．今天，我们就可直接给出统一的结论.

如文[4]给出的数学奥林匹克问题.

命题1[4]圆内接四边形ABCD的两组对边AD和BC分别交于点E和F，过点B、D分别作AB和CD的切线交于点P，则E、P、F三点共线.

此命题是帕斯卡定理的特殊情况，当二次曲线的内接六边形退化为四边形时，其中六边形的一双对边退化为二次曲线的一对切线，则这一对切线的交点与另两双对边的交点共线.

2.2 注重《高等几何》作用的发挥

高等几何的丰富内容，对于欧氏几何学习和研究有着重要的指导作用.

2.2.1 避免低层次问题的重复“发现”

当前，在初等数学研究中，也出现了一种不良的现象：就是将《高等几何》中的一些特殊问题，作为“新”发现命题，而用解析几何方法进行繁杂的证明，这对数学的发展是没有好处的．因此，教师应该注重用《高等几何》研究欧氏几何问题，并加强《高等几何》的学习.关于这一点，在文[5～6]给出的“新”结论，其实都重复了前人的研究成果.

命题2[5]若一条直线被双曲线及两条渐线所截，则夹在双曲线与两条渐线间的线段长相等.

命题3[6]过双曲线上一点P作双曲线的切线交渐线与点A、B，则

1）PA=PB；

2）ΔOAB（O为双曲线的中心）的面积为定值.

显然命题3第一结论为命题1的特例．命题2和命题3是朱德祥《高等几何》教材中例题和习题[3]．

2.2.2 揭示命题的内涵

射影解法研究几何命题的优越性在于，不仅可以给出命题的解法，更重要可以揭示命题的内涵.

如对于广义的蝴蝶定理，有以下结论.

命题4 如图3．过二次曲线Γ弦AB外一点M引Γ的两弦CD，EF分别交弦AB于G、H，CF、ED分别交AB于P、Q；，记AG ＝ a，BH = b，GH = r，PG = X，QH = y，则

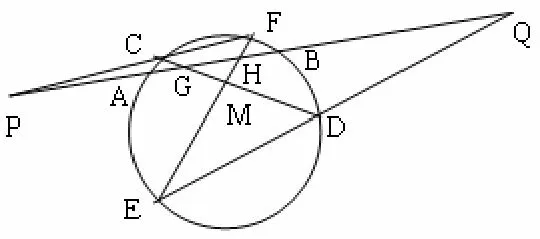
图3

显然，当r = 0，即G、H、M三点合于AB上一点，为Candy蝴蝶形式

再当a = b时，为蝴蝶形式

此时，如图3．若当ED//AB时，则在射影几何中，直线ED与直线AB相交于无穷远点Q∞，即QH = y→∞．于是，（1）为：

推论4 二次曲线Γ弦AB外一点M引Γ的两弦CD，EF分别交弦AB于G、H，CF、ED分别交AB于P、Q，记AG ＝ a，BH = b，GH = r，PG = X，QH = y，则

（2）当ED//AB//CF时，ab=．

如图3．若再当直线CF与直线AB相交于无穷远点P∞，即PG=X→∞．于是，有结论推论4的（2）成立．

射影几何将文[7]的定理1～4统一起来，并且给出新结论，对于蝴蝶定理的认识，增添新的气息．

2.2.3 给出古老问题的新“结论”

在射影几何中，由于线束的交比可以用线束的夹角表示．因此，又可得到广义蝴蝶定理的新结论．

命题5[8]如图4．过二次曲线Γ弦AB上一点M引Γ的两弦CD，EF，CF、ED分别交AB于P、Q，记∠PCM = α，∠QCM = β，∠ACM = γ，∠BCM = θ，则

此时，若以CD为x轴，建立直角坐标系，则线束C（PQAB）斜率分别为：KCP=－tanα，则

图4

推论5 过二次曲线Γ弦AB上一点M引Γ的两弦CD，EF，CF、ED分别交AB于P、Q，若线束C（PQAB）斜率分别为：KCP，KCQ，KCA，KCB，则（4）成立.

显然，将蝴蝶定理的线段关系（1），转换为斜率关系（4），极大地丰富了蝴蝶定理的内涵.

[1]吕建恒.数学奥林匹克问题[J].中等数学，2008（2）：47-49.

[2]周振荣，赵临龙.高等几何[M].武汉：华中师范大学出版社，2013.

[3]朱德祥.高等几何[M].北京：高等教育出版社，1998.

[4]吕建恒.数学奥林匹克问题[J].中等数学，2008（7）：48-49.

[5]吕中伟.双曲线一个几何性质的应用研究[J].中学数学教学参考（高中），2006（5）：32-33.

[6]姚光伟.双曲线切线的一条性质[J].中学数学教学参考（高中），2006（7）：54.

[7]张殿书.和圆中内接碟形相关的系列有趣性质[J].数学通报，2011（9）：58-60.

[8]赵临龙.蝴蝶定理线束夹角表达形式的研究[J].河南科学，2012（4）：404-406.

（责任编辑：张新玲）

The Implications of the Prospective Method of a Geometric Proposition

ZHAO Linlong
(Institute of Mathematics and Applied Mathematics, Ankang University, 725000, China)

This paper uses the relationship between pole and polar line of prospective geometry and a prospective method to solve a geometric proposition. It reveals the inner relation of propositions. Two implications are noticeable in this study: Higher Geometry shall be learned and researched; Higher Geometry’s function shall be given full play.

Euclidean geometry; prospective geometry; poles; epipolar line

O18

A

1009-8135（2015）03-0011-03

2015-01-11

赵临龙（1960-），男，陕西西安人，安康学院教授，主要研究几何学．

陕西特色专业建设项目（2011-59）；安康学院重点学科建设项目（ZDXKZX201318）阶段性成果