利用环形子孔径拼接法检测非球面反射镜

李 江，杨朋利，李文婷，王 芝，安 静，冯 婕，马爱秋，付晓庆

引言

在传统非球面面形检测中，通常需要搭建辅助光路进行测试，虽然检测精度较高，但由于辅助光学元件受尺寸限制，所以检测也具有一定局限性［1－3］。环形子孔径拼接检测技术作为非球面面形的一种检测方法，最早是由Arizona大学光学中心的Y.M.Liu教授在1988年提出，并进行了实验验证，证明了该方法的可行性。随着计算机控制技术和数据处理技术的不断发展，美国QED公司于2003年研制出自动拼接干涉仪SSI，它能够检测具有一定非球面度且口径小于200mm的非球面［4］。本文利用Zygo干涉仪来实现非球面环形子孔径检测，实现对口径为8mm的非球面反射镜的拼接检测，并将使用无像差点法测得的全口径面形数据与拼接检测所得的面形数据进行了比对。

1 环形子孔径拼接检测原理与拼接算法

1.1 环形子孔径拼接检测原理

采用Zygo干涉仪进行测试，测试原理如图1所示，由Zygo干涉仪发出的平面波通过标准镜之后，汇聚成点后发散成为标准球面波，沿图中箭头所标方向移动待测非球面，可以使具有不同半径的参考球面波与待测非球面不同的环带部分进行匹配，从而获得各环带的面形图，通过拼接算法将各环带拼接在一起，即可获得全口径的面形信息。具体实现过程如图2所示。

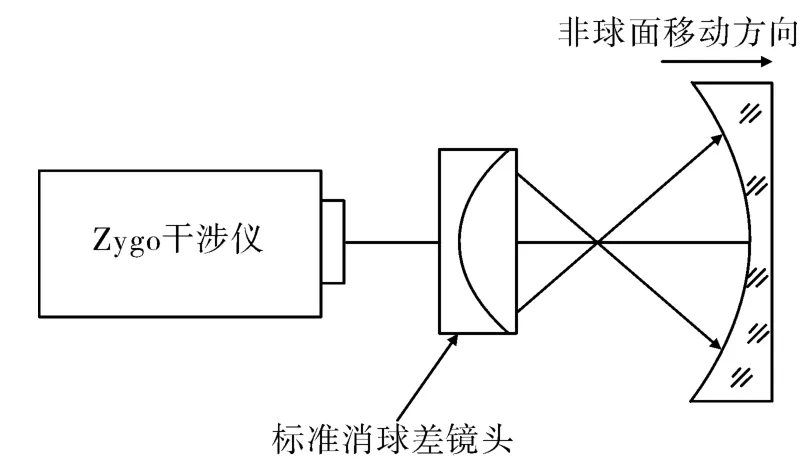
图1 环形子孔径拼接检测原理示意图Fig.1 Sketch of annular sub－aperture stitching testing

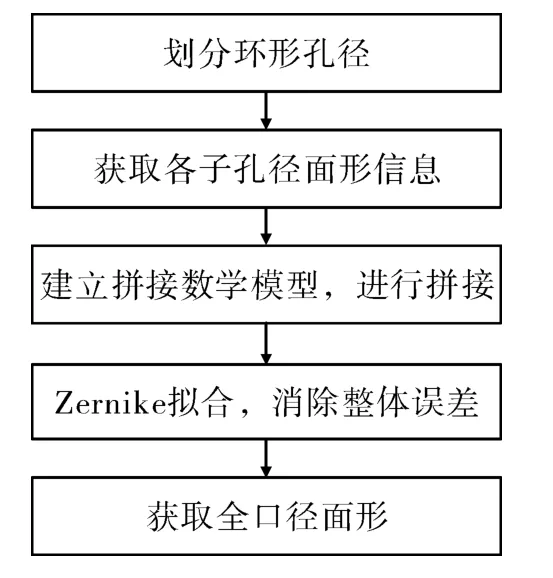
图2 环形子孔径拼接检测的过程示意图Fig.2 Process of annular sub－aperture stitching testing

1.2 环形子孔径的划分依据

在整个非球面子孔径拼接检测中，子孔径的划分直接决定着拼接算法的数据运算量以及拼接检测精度［5－6］，所以第一步要做的是合理划分环带子孔径，划分的依据是奈奎斯特采样定理［7－8］，即要寻找能够保证成像CCD上至少有2个像素点的宽度用来显示一条条纹的位置［9］，这个位置即对应子孔径的边界。根据这种划分依据，便可以得到下式：

式中：n（x）为非球面子午线方程；s（x）为子孔径的对应球面波方程；p为干涉仪上成像CCD的可用像素数（CCD像素为p×q，p≤q）；D为待测非球面口径；λ为干涉仪中激光器发出激光的波长。

1.3 环形子孔径的拼接算法

通常逐次拼接算法随着拼接次数的增多，累积误差不断增大，对拼接精度影响很大［10］，所以本文提出基于最小二乘法的全局优化拼接算法。当拼接区域大于2个时，假设共有N个子孔径拼接，可以先将其中任一个子孔径作为基准，为了便于定位和测量，一般选择非球面中心区域的子孔径组作为参考标准，假设其他子孔径相对基准子孔径的调整系数分别为（a1，b1，c1，d1），（a2，b2，c2，d2），…，（aN－1，bN－1，cN－1，dN－1），则其他子孔径尾箱分布与参考孔径的位相分布关系为

利用最小二乘法，使得所有重叠区域位相差的平方和值为最小，可得：

式中m为每个重叠区域多的采样点数，所有重叠区域的数目为N－1，利用最小二乘法，对（3）式中各个系数分别求偏导并令其值为零，可得：

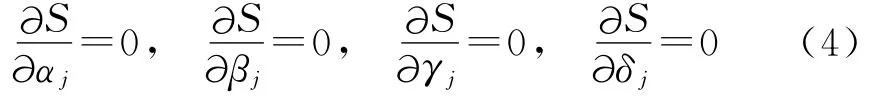
式中1≤j≤N－1，利用上式就可以得到每个子孔径相对基准子孔径的拼接因子，从而把所有子孔径的位相数据统一到相同的参考面上。最后将拼接好的面形进行Zernike拟合，剔除平移、倾斜、离焦对面型数据的影响，即整个环形子孔径的拼接过程。

2 环形子孔径拼接实验及结果

为了验证上述拼接算法对非球面的检测精度，现对口径为8mm，顶点球半径为43.95mm的旋转双曲面反射镜进行实验验证。该被测面既可采用无像差点法检测，也可采用子孔径拼接检测，从而有利于验证拼接算法的正确性和可行性。该被测面全口径满足奈奎斯特采样定理，采用子孔径拼接法将全口径面形划分为2个子孔径，子孔径的划分如图3所示，将整个口径分为2个环带，图中阴影部分为区域重合部分。具体实验装置如图4所示。

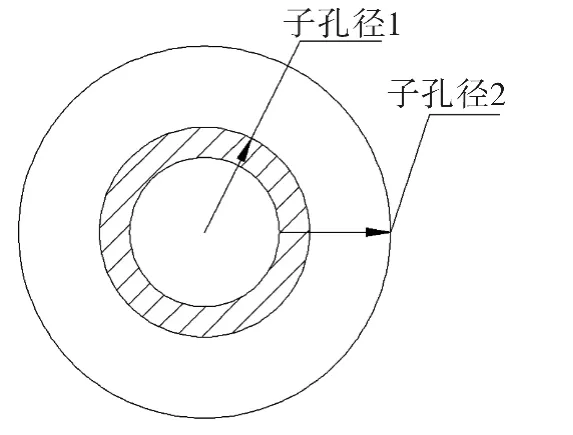
图3 环带划分图Fig.3 Two sub－apertures

图4 实验装置图Fig.4 Experimental setup

首先通过移动待测非球面，分别获得子孔径1和子孔径2的面形图，如图5所示。

图5 各子孔径的面形图Fig.5 Measured sub－apertures

将各子孔径的面型数据作最小二乘法处理，进而获得拼接因子，然后再将拼接在一起的面形进行Zernike多项式拟合，用以消掉调整误差，最终得到全口径的拼接检测结果，如图6所示，面形数据以λ作为计量基准，其中λ＝632.8nm。

图6 拼接检测结果Fig.6 Stitching result

为验证拼接算法的正确性和稳定性，现将全口径被测面形按不同尺寸对子孔径进行重新划分，改变子径的边界位置，并进行多组重复性实验，各组实验结果如表1所示。

表1 各组重复性实验最终拼接结果 λTable 1 Final stitching results for repeated experiments

从表1的实验结果可以看出，重复性实验具有较高的稳定性，基本可以满足干涉测量的要求。

为验证拼接检测的正确性，搭建图7所示光路，实现无像差点法检测全口径。为进一步排除装调误差对辅助验证结果的影响，在得到无像差点法的检测面形之后，继续进行Zernike多项式拟合，剔除Zernike多项式前4项之后的结果，如图8所示，检测结果见表2。

图7 搭建的无像差点法测试光路Fig.7 Setup of testing light path with aberration－free point method

图8 无像差点法检测结果Fig.8 Testing result of aberration－free point method

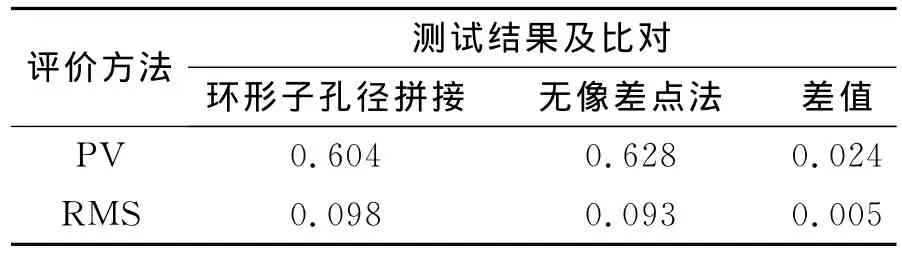
表2 拼接测试及其比对 λTable 2 Result of testing and comparison

从表2可以看出，环形子孔径拼接检测结果与无像差点法最终检测结果PV值相差0.024λ，RMS值相差0.005λ。验证了拼接算法的正确性和可行性。

3 结论

本文利用实验室现有Zygo干涉仪对一口径为8mm的非球面实现了环形子孔径拼接检测，另搭建无像差点法测试光路对检测结果进行验证，试验结果表明：环形子孔径拼接检测测量误差小于1／20λ，这一结果充分说明了利用Zygo干涉仪对非球面进行环形子孔径拼接检测的可行性，为今后非球面的检测工作提供了一种可行的方法。

［1］ Wang Xiaokun，Wang Lihui，Zhang Xuejun.Testing asphere by sub－aperture stitching interferometric method［J］.Optics and Precision Engineering，2007，15（2）：192－198.

王孝坤，王丽辉，张学军.子孔径拼接干涉法检测非球面［J］.光学精密工程，2007，15（2）：192－198.

［2］ Zhang Rongzhu，Shi Qikai，Cai Bangwei，et al.Subaperture stitching interferometric detection experimental［J］.Optical Technology，2004，30（2）：173－175.

张蓉竹，石琪凯，蔡邦维，等.子孔径拼接干涉检测实验研究［J］.光学技术，2004，30（2）：173－175.

［3］ Wang Xiaokun，Zheng Ligong，Zhang Xuejun，et al.Testing an off－axis asphere by subaperture stitching interferometry［J］.Acta Photonica Sinica，2011，40（1）：92－97.

王孝坤，郑立功，张学军，等.子孔径拼接干涉检测离轴非球面研究［J］.光子学报，2011，40（1）：92－97.

［4］ Ji Bo.Testing asphere optical components by subapertue stitching Interferometer［D］.Nanjing：Nanjing University of Science and Technology，2008.12－29.

季波.子孔径拼接干涉检测非球面光学元件［D］.南京：南京理工大学，2008.12－29.

［5］ Tiziani H J，Reiehelt S，Prub C，et al.Testing of aspheric surfaces［J］.SPIE，2001，4440：109－119.

［6］ Hou Xi，Wu Fan.Annular sub－aperture interferometric testing technique for large aspheric surface［J］.SPIE，2005，5786：113－121.

［7］ Sasaki K，Ono A.Optical aspheric surface profiler using phase shift interferferometer：US，5416586［P］.1991－01－01.

［8］ Mauro M，Luca P.Interferometric testing of annular aperture［J］.SPIE，1992，1781：241－248.

［9］ Chen Shanyong.Geometrical approach to sub－aperture stitching interferometry for aspheric surfaces［D］.Changsha：National University of Defense Technology，2006：1－16.

陈善勇.非球面子孔径拼接干涉测量的几何方法研究［D］.长沙：国防科学技术大学，2006：1－16.

［10］Bai Jian，Cheng Shangyi，Yang Guoguang.Subaperture aligment technique for large aperture mirrors［J］.Acta Optica Sinica，1997，17（7）：953－956.

白剑，程上彝，杨国光.大口径镜面的多孔径拼接技术［J］.光学学报，1997，17（7）：953－956.