回转件弯扭测量系统及其不确定度分析

李志凤，赵登峰，马国鹭，曾国英，卢 展

引言

随着现代工程技术的飞速发展，特别是石化、电力、航空、能源和工程机械等行业，需要对其回转部件的振动特性进行在线检测。在机械制造中，对旋转状态轴系部件的在线振动测量和分析，已成为鉴别和确定部件工作可靠性、实现设备高精度测量和故障诊断的重要手段［1］。回转机械轴系的振动主要表现为弯曲振动和扭转振动。在以往的转子动力学分析中，很多学者将扭转振动与弯曲振动分开来研究，而忽略这些振动形式之间相互耦合的复杂关系［2－3］。对于汽轮发电机组这类大型回转机械，弯曲振动和扭转振动的危害较大，其表现之一是机组的次同步振荡。机床的轴系在高速切削过程中发生弯扭振动时，会影响加工精度［4］。因此，对回转件轴系振动的综合同步监测十分必要。

旋转状态轴系的振动测量方法可分为机械法、电测法和光测法3类。前2种测量方法存在安装不便、动态特性差、测量精度较低、受测量环境限制较大等缺点，因此这两类测量方法的应用受到很大限制［5－6］。基于激光多普勒效应的振动检测技术是近几年发展起来的光学测振技术，具有空间分辨率高、动态测量范围大、适应性强、非接触测量等优点，其检测的频率与幅值范围几乎涵盖了传统的各种机械振动检测方法［7－8］。但是无论何种振动测量方式，在测量过程中都会受到设备、人员、环境、被测对象等方面不同程度的影响而引入误差，最终影响测量精度［9］。测量不确定度表示由于测量误差的存在而对测量结果不可信的程度，表征被测量之值的分散性［10］。因此，为了得到更高精度的测量结果，准确诊断设备故障部位，保障设备稳定安全运行，对振动测量系统的测量不确定度分析就显得尤为必要。

本文将激光多普勒振动检测技术应用于回转机械轴系部件的在线振动监测。基于激光多普勒的频移原理，结合光学差拍及参考光技术，开发能同时测量轴系部件弯曲振动、扭转振动和轴系旋转速度的空间综合振动测量系统。同时，针对影响多普勒信号的因素，如气温、气压、湿度等引起激光波长变化的环境参数、光学组件、测量对象等其他参数进行了分析和探讨，并给出了具体影响参数的测量不确定度。

1 回转件弯扭振动测量系统

基于激光多普勒效应测量转轴的回转不均匀性和扭转振动是国际上近年来发展的新技术［11］。利用激光的高方向性、单色性、相干性等特性以及特殊的光学装置产生两束强度相等的平行光束。当激光束照射到转轴表面时，轴表面的线速度使散射光产生多普勒频移，频移量的瞬间值表征了轴表面的综合振动情况。本文设计的测量系统光学原理图如图1所示。

图1 测量系统光路原理图Fig.1 Optical path diagram of measuring system

激光器发出的单色入射激光，经立方分束器和反射棱镜等分光装置分成强度相等且间距为d的2路平行光束，测量高速转轴表面测量点的水平速度。到达被测转轴表面同一截面的测量光束1、2分别在转轴表面被散射，散射光束部分沿原路返回，经平凸透镜和立方分束器后分别与相应参考光束发生干涉，获得测量光束与参考光束的差拍频率，然后通过2个不同方向的光电探测器完成信号的接收。

根据多普勒频移原理和轴系在旋转状态下的综合振动分析（如图2）可以获得2个探测器的差拍频率为

式中：fA、fB分别为测量点A、B的多普勒频移值；λ为激光波长；Vx为被测部件弯曲振动沿x轴方向的速度分量；VAx、VBx分别为A、B点的线速度沿x轴方向的速度分量。

图2 不同振动方向速度分解Fig.2 Vibration velocity decomposition in different directions

结合差拍频率fA、fB和A、B点的线速度关系式VA＝VB＝2πNR，可以推出回转部件的瞬时转速和弯曲振动沿x轴方向的速度分量分别为

扭转振动的具体表现是转轴速度的随机波动，因此瞬时转速值就表征了旋转部件的扭转振动特征。通过（3）式、（4）式可以得出，被测转轴的瞬时转速与2个探测器的频移之和成正比，弯曲振动沿x轴方向的速度分量与2个探测器的频移之差成正比，实现了扭转振动与弯曲振动的独立测量，且扭振测量不受轴系横振因素的影响。

2 综合振动测量实验

激光多普勒振动测量对防震要求较高［12］。在综合振动测量中，外界随机振动及转轴运转产生的振动都会影响测量结果的精度。振动会使多普勒信号减弱，甚至得不到多普勒频移信息，因此实验时采用卓立汉光有限公司的自动平衡光学隔振平台。它利用自身的隔振效果和固有频率等特点，能有效避开环境振动所产生的共振现象，控制振幅放大，减少振动传递率，消除环境振动对扭弯振动测量的影响。具体光学实验系统及数据采集分析系统如图3所示。

图3 综合振动测量实验Fig.3 Comprehensive vibration measurement experiment

实验时首先固定激光器的位置，使其尽量与光学平台边缘线平行；调整滤光镜、立方分束器的位置，使得激光束垂直入射到分束器BS1中。为了方便实验调整，减少因分束器BS1与立方反射棱镜M，分束器BS2和BS3之间的不平行以及这两者之间的光程差引起的误差，分别将分束器BS1和反射棱镜M、分束器BS2和BS3用盎司紫外固化光学胶粘贴在一起，保证2个光束测量平行误差控制在10－4rad以内。转轴和2个光电探测器都在平凸透镜的焦点处。实验时转轴转速为60r／min（本实验选用带微型齿轮减速器的交流伺服电机，其具有运转平稳、噪声低、安全可靠等特点），根据奈奎斯特定理，设置数据采集系统采样频率为5MHz，采样数为采样频率的十分之一。光电探测器A、B接收的后向散射光首先经过适当的预处理，然后进行数据采集，并通过Matlab进行数字信号处理。在Matlab中提取频率随时间变化的数据，每一帧数据提取一个频率的平均值，测量结果及其残差υi的计算如表1。

表1 测量结果和残差计算 kHzTable 1 Measuring results and residual calculation

3 弯扭测量系统不确定度分析

（3）式、（4）式表明，影响回转部件瞬时转速N和弯曲振动速度测量的因素有：多普勒频移值fA与fB，激光器输出波长λ和2个测量光束的距离d。因为2路光束采用完全相同的光学元件，且都是将测量信号传输至同一数据分析系统，从而获得fA与fB，因此可以认为fA与fB强相关，即相关系数r（fA，fB）＝1。假设f1＝fA＋fB，f2＝fA－fB，则

式中：uc（f1）和uc（f2）分别为f1和f2的A类或B类合成标准不确定度；u（fA）和u（fB）分别为光电探测器A、B的频差的A类或B类标准不确定度。

在采用激光多普勒原理测量旋转轴弯扭振动时，由于分光镜制造精度不够，产生光束偏移，反射棱镜反射率，外界随机振动以及杂散光等都会引起测量不确定度的产生，而¯fA与¯fB是通过多次重复测量获得，故可以认为外界随机振动以及杂散光引起的不确定度已包含在uc（f1）和uc（f2）中。本系统采用镀有400nm～700nm波长范围宽带介质膜的等腰直角立方反射棱镜，其平均反射率大于99%，而且该测量方法是收集待测转轴的后向散射光，光束在小角度（±1°）内偏移，对测量精度的影响极小，故分光镜与反射镜等设备参量引起的不确定度可不予以考虑。

根据测量条件可知，（3）式、（4）式中各参量彼此不相关，由不确定度传播律可得测量值N和Vx的方差表达式如下：

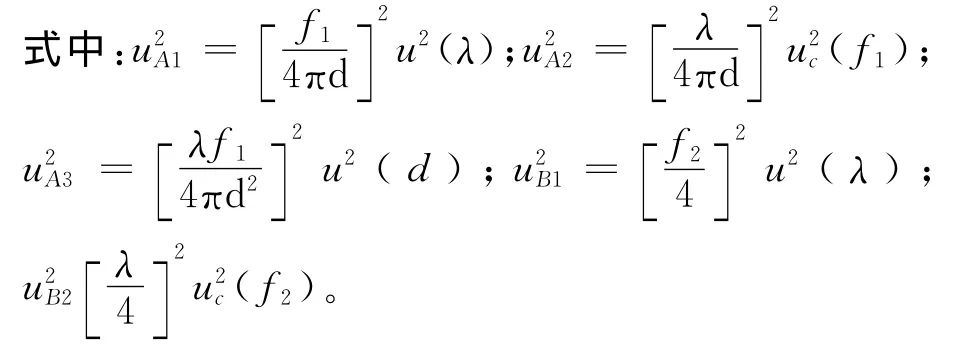
根据国家计量技术规范JJF1059－1999《测量不确定度的评定与表示》［9］，测量系统的扩展不确定度方程如下：

式中：k为包含因子；uc为测量系统参量的合成标准不确定度。

因数据采集时为连续采集，且每次都是在相同数据采集系统及相等设定转速条件下进行，故该实验可看成是在重复性条件下进行的10次独立重复观测实验。由标准不确定度的A类评定方法及贝塞尔公式，结合实验所得数据（表1）可得：

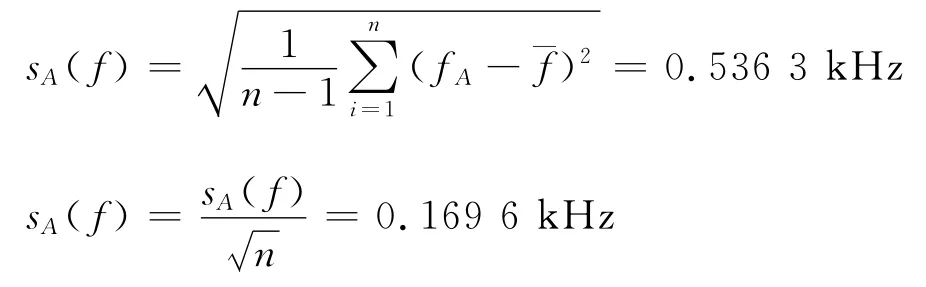
式中：sA（f）为光电探测器A所测频率的实验标准差；fA为光电探测器A所测一帧数据频差的平均值；¯f为10次测量频差的平均值；sA（¯f）为10次测量频差平均值的实验标准差。

fA的标准不确定度为uA（¯f）＝sA（¯f）＝0.169 6kHz，其自由度υA＝n－1＝9。

类似地可求得光电探测器B所测频率的A类标准不确定度为uB（¯f）＝0.165 4kHz，自由度υB＝n－1＝9。

所以

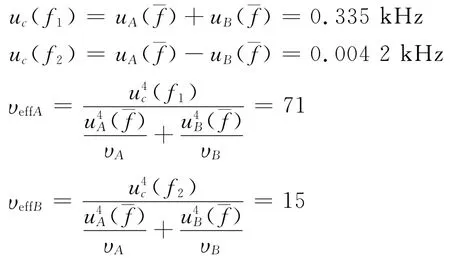
式中，υeffA和υeffB分别为uc（f1）和uc（f2）的有效自由度。

（3）式、（4）式表明，利用激光多普勒原理进行振动测量时，波长与转速、弯曲振动速度均成正比，波长的不确定度直接影响了测量系统所能达到的最高精度。随着现代激光技术的发展，使得激光稳频和复现性可以实现很高的精度，由激光源频率所致的波长不确定度一般在10－8量级以上［13］。在实际应用中，激光波长随空气折射率n的变化而变化。而空气折射率n主要受测量环境的温度、气压、湿度的影响。因此，要得到精确测量结果，须考虑空气折射率引起的激光波长的不确定度。

当环境条件偏离标准状态（P＝101.325kPa、t＝20℃，h＝1 333.22Pa）时，根据Beugt Edlen经验公式［14］得出折射率随环境条件变化的公式如下：

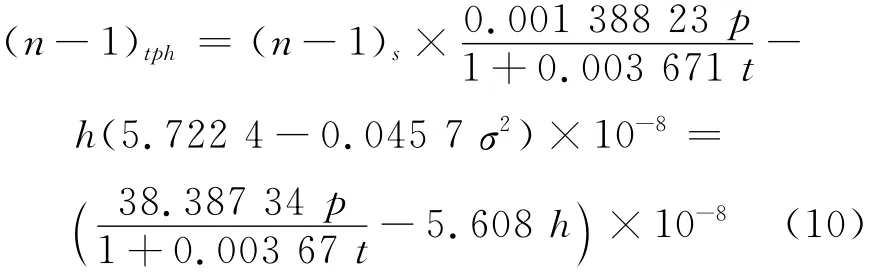
假设环境温度t，气压P，湿度h的测量不确定度分别为u（t）、u（p）和u（h），将n分别对t、p、h求偏导数即得灵敏系数：

所以

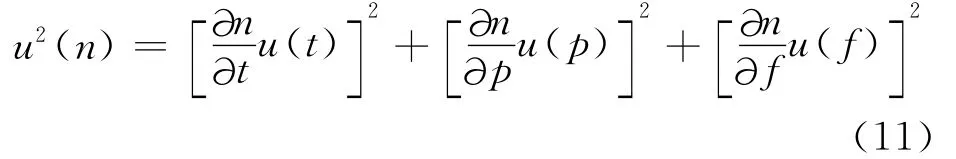
式中，u（n）为折射率n的B类标准不确定度。

多次实验表明，温差以等概率落于区间－1℃至1℃之间.假设气压变化值为±50Pa，相对湿度变化值为±5%RH，均服从均匀分布，其包含因子k为，所以温度、气压、湿度的标准不确定度为

将（12）式带入（11）式可得：

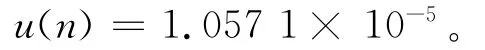
因为空气中波长λ与真空中波长λ0有关系式λ＝λ0／n，由不确定度传播律可得：

取n＝n0＝1，λ0＝632.82nm，则u1（λ）＝6.689×10－9mm

激光器校准证书给出，激光源频率所致的波长不确定度为1.05×10－9mm，且该不确定度与空气折射率变化引起波长变化的不确定度u1（λ）无关，故波长λ的合成标准不确定度为u（λ）＝6.763 3×10－9mm。

实验时2个测量光束的距离由测量系统中的立方分束器BS2和BS3决定。当测量系统所处环境温度变化时，其体积发生微小变化。本系统采用BK7材质立方分束器和反射棱镜，其具有耐高温与化学性能好等优点，且膨胀系数低（在10－7数量级），在温差较小的情况下，可估计其标准不确定度在10－8mm至10－9mm数量级，由（7）式可以估计2个测量光束距离d的不确定度与波长、频移值的不确定度相比甚小，可忽略不计。

因此，将uc（f1）、uc（f2）和u1（λ）的值分别带入（7）式、（8）式可算出多普勒频移和波长的不确定度分别对瞬时转速N和Vx的不确定度贡献为

4 结论

本文将激光多普勒振动检测技术应用于回转机械轴系部件弯扭振动的在线监测，通过构建实验原理方案，推导了光路部分的数学模型，并就测量过程中可能引起误差的参量进行了不确定度分析。根据以上分析可知，利用激光多普勒的频移原理进行振动测量时，激光器波长、光学镜组等参量引起的误差较小（几乎可以忽略不计），测量不确定度主要来源于多普勒频移值fA和fB，其反应了各种随机因素，如测量系统的延时误差、电路噪声干扰、外界随机振动等。结合抗振技术，选择更优的信号处理方法，能够有效减小系统误差，提高测量精度，实现轴系振动特性的准确检测。

［1］ Sang Bo，Zhao Hong，Wang Xueli，et al.Research on the 2－D laser doppler vibration tester ［J］.Acta Photonica Sinica，2001，30（5）：614－617.

桑波，赵宏，王学礼，等.2－D激光多普勒振动测试仪的研究［J］.光子学报，2001，30（5）：614－617.

［2］ Tong Qingbin，Ma Huiping，Liu Lihua，et al.Key technologys study on radial vibration detection system of high－speed rotating machinery ［J］.Chinese Journal of Scientific Instrument，2011，32（5）：1026－1032.

佟庆彬，马惠萍，刘丽华，等.高速旋转机械径向振动检测系统关键技术研究［J］.仪器仪表学报，2011，32（5）：1026－1032.

［3］ Zhang Yong，Jiang Zikang.Analysis of the coupled

flexural torsional vibrations of rotary shaft systems［J］.Journal of Tsinghua Universrty：Science and Technology，2000，40（6）：80－83.

张勇，蒋滋康.旋转轴系弯曲振动与扭转振动耦合的分析［J］.清华大学学报：自然科学版，2000，40（6）：80－83.

［4］ Guo Li，Li Bo.Reviewed of the shafting torsional vibration measurement method ［J］.Grinder and Grinding，2000（3）：53－56.

郭力，李波.轴系扭转振动测量方法评述［J］.磨床与磨削，2000（3）：53－56.

［5］ Wang Qingyun，Wang Huilin，Vibration test and analysis of the instrument used in processing center［J］.Mechanical Research ＆ Application，2011（3）：175－183.

王庆云，王辉林.加工中心旋转机械振动测试与故障分析［J］.机械研究与应用，2011（3）：175－183.

［6］ Chen Changying.A new type vibration sensor of laser doppler technology ［J］.Opto－Electronic Engineering，1997，24（2）：12－17.

陈长缨.一种新型激光多普勒振动传感器［J］.光电工程，1997，24（2）：12－17.

［7］ Lyu Hongshi，Liu Bin.Latest development of laser doppler technique in vibration measurement［J］.Laser Technology，2005，29（2）：176－180.

吕宏诗，刘彬.激光多普勒测振技术的最新进展［J］.激光技术，2005，29（2）：176－180.

［8］ Bell J R，Rothberg S J.Rotational vibration measurements using laser vibrometry：comprehensive theory and practical application ［J］.Journal of Sound and Vibration，2000，238（4）：673－690.

［9］ The Quality and Technical Supervision Division Metering Group.Evaluation and expression of uncertainty in measurement guide［M］.Beijing：China Metrology Press，2005.国家质量技术监督局计量司.测量不确定度评定与表示指南［M］.北京：中国计量出版社，2005.

［10］Chen Hao，Lu Hen，He Yong，et al.Uncertainty analysis and design of long focal length measuring system ［J］.Opto－Electronic Engineering，2013，40（6）：71－77.

陈好，陆衡，何勇，等.长焦距测量仪的设计和测量不确定度分析［J］.光电工程，2013，40（6）：71－77.

［11］Yue Kaiduan，Tang Jingyuan，Zhang Wending.Torsional vibration measuring by doppler technology［J］.Acta Photonica Sinica，2001，30（7）：868－870.

乐开端，唐经源，张文定.回转机械扭转测量技术研究［J］.光子学报，2001，30（7）：868－870.

［12］Liu Dan，Zheng Bin，Guo Hualing，et al.Micro－vibration measuring technology based on heterodyne interference［J］.Journal of Applied Optics，2014，35（8）：858－861.

刘丹，郑宾，郭华玲，等.基于外差干涉的微振动测量技术研究［J］.应用光学，2014，35（8）：858－861.

［13］Xue Mei，Xian Yimin Yu Dongsheng.Automatic real－time compensation of wavelength of laser interferometer［J］.Tool Engineering，2005，39（8）：90－92.

薛梅，羡一民，于东升.激光干涉仪波长的自动实时补偿［J］.工具技术，2005，39（8）：90－92.

［14］Liu Jun，Mu Haihua，Sun Yeye，et al.Error analysis and compensation in laser interferometry ［J］.Machine Tool ＆ Hydraulics，2006（9）：181－184.

刘君，穆海华，孙业业，等.激光干涉测量中的误差分析与补偿［J］.机床与液压，2006（9）：181－184.