小模糊尺度下运动模糊方向鉴别算法研究

付 强，孙秀霞，刘树光，洪 洋，彭 轲

引言

摄像机的振动、摇晃或旋转，导致高动态环境下视觉导航过程中所观测到的场景图像会发生不同程度的运动模糊。运动模糊多种多样，包括匀速直线运动、变速运动、周期运动等，在一定条件下，变速运动，周期运动等非匀速直线运动可以看成许多个匀速直线运动的合成。因而运动模糊考虑成由匀速直线运动造成的，更具有一般性和普遍性。而且当照相机的曝光时间非常短时，就可以把运动模糊近似为匀速直线运动模糊处理［1］。精确鉴别运动模糊图像的模糊参数是运动模糊图像复原和超分辨率重建的前提条件，且方向估计是参数估计中的基础。

目前，国内外许多学者对运动模糊图像的模糊方向估计问题有一定的研究，国外主要由Moghaddam和Jamzad对运动模糊参数识别进行系统研究，提出Radon变换对运动模糊角度进行鉴别，运用模糊集进行参数辨识，但其精度依赖于模糊集图像主瓣宽度的测量，测量误差导致其算法的不精确［2－3］。比较经典的方法主要有：方向微分乘子鉴别运动方向、模糊图像倒频谱分析运动方向、Hough变换估计运动方向及Radon变换估计运动方向等［4－8］。这些算法在图像存在较大的运动模糊尺度时可以得到比较精确的参数鉴别结果，而对于小尺度运动模糊图像的方向估计精度不高，主要因为小尺度模糊图像的频谱图方向特征不明显。本文在郭红伟等人［9］和孔勇奇等人［10］研究模糊图像二次傅里叶频谱的工作基础上，针对小尺度运动模糊图像的频谱特点进行处理。首先对小尺度运动模糊图像的频谱进行细化，在二次傅里叶变换后通过中值滤波对频谱图像进行处理，再选用灰度中值作为阈值进行二值化，在传统算法去除中心十字亮线的基础上提出去除中心亮斑，然后用投影公式计算出亮条纹方向以得到小尺度模糊图像的方向估计。为小尺度运动模糊图像的方向鉴别提供了一种新思路。

1 小尺度运动模糊图像分析

1.1 运动模糊图像模型

根据成像系统的一般特性，在线性位移不变系统中图像的退化就是成像系统的退化加上额外的系统噪声而形成的，图像退化的一般模型可以表示为

式中：y为模糊图像；x为原始图像；k为模糊核；w为设定的噪声。

运动模糊图像的点扩散函数k的一般表达式为

式中：L表示曝光时间内相机的镜头与目标之间相对移动的尺度大小；θ表示曝光时间内相机的镜头与目标之间相对运动的方向。由此可得，模糊核由运动模糊方向参数θ及运动模糊长度参数L决定，它们是运动模糊图像的2个重要参数。一般情况下，当10＜L≤80，大多数鉴别算法的角度和尺度估计均无误差，当L≤10时，角度估计会出现误差。因此，本文将重点分析小尺度运动模糊图像，即模糊尺度L≤10时，模糊方向估计出现误差的原因并实现精确鉴别。

1.2 小尺度运动模糊图像频谱特性

在使用同一模糊方向鉴别算法的情况下，小尺度运动模糊图像存在误差而大尺度运动模糊图像不存在误差，所以可以将大尺度与小尺度运动模糊图像进行对比找出其差异之处，分析出小尺度运动模糊图像在鉴别方向时出现误差的原因。因此，本文首先对具有相同运动模糊方向的不同尺度图像进行对比，对比结果如图1所示。

图1 大小尺度运动模糊图像对比Fig.1 Comparison of motion－blurred images

从图1可以看出，大尺度运动模糊图像的频谱暗条纹与运动方向相互垂直，因此，大多数现有算法都是在频域中对暗条纹进行直线检测完成运动模糊图像的模糊方向鉴别。然而在小尺度情况下，频谱图像的暗条纹边缘轮廓变得弯曲，直接利用暗条纹方向与运动模糊方向之间的垂直关系无法精确得到小尺度运动模糊图像的模糊方向。因此，对小尺度运动模糊图像的频谱进行处理，使其频谱方向特征更加明显，是实现其模糊方向鉴别的一种可选方案。

2 小尺度运动模糊图像方向鉴别

本文拟解决运动模糊图像在小尺度模糊参数下的方向鉴别问题，算法最主要的任务是对频谱进行处理，达到可以精确提取出方向特征的要求，包括频谱细化、频谱二值化和投影变换3个大部分。本文提出的小尺度运动模糊图像模糊方向鉴别算法流程如图2所示。

图2 小尺度运动模糊图像方向鉴别流程图Fig.2 Flow chart of direction detection of smallscale motion blur image

2.1 频谱细化算法设计

注意到当模糊尺度过小，一次傅里叶变换的频谱图像暗条纹轮廓变得弯曲，并且运动模糊图像的尺度越小，条纹宽度越宽，无法精确提取出条纹方向特征以致传统模糊方向鉴别方法出现误差。要想实现对小尺度运动模糊图像模糊方向的精确鉴别，首先得对频谱进行细化。文献［9］提出将模糊图像进行二次傅里叶变换可以得到更加细化的频谱图，文献［2］指出模糊图像二次傅里叶变换频谱图中亮线方向即为运动模糊方向，因此，本文首先对运动模糊图像进行二次傅里叶变换，如图3所示。

图3 二次傅里叶变换频谱图Fig.3 Twice Fourier spectrograms

从图3可以看出，尽管二次傅里叶变换能够达到细化频谱的效果，但是相较于大尺度运动模糊图像的细长亮线，小尺度运动模糊图像即使在二次傅里叶变换频谱图中的亮线也十分短，频谱的方向特征无法精确检测。为了使亮线更加突出，将二次傅里叶频谱图中的大量孤立点看成“噪声”，考虑到中值滤波可以保护边缘信息，因此，本文采用中值滤波器对其进行“去噪”，进一步提高细化频谱的效果。通过利用中值滤波进行“去噪”，还可以克服在二值化过程中对阈值选取不恰当的情形。

2.2 频谱二值化算法设计

小尺度运动模糊图像频谱的二值化有利于更好的将方向特征在二次频谱中划分出来，而灰度阈值选取不恰当会给整个二值图像造成噪点。文献［9］提出采用排序为100的像素灰度作为阈值进行二值化，可是对于不同尺度的模糊图像亮点个数并不同。因此，本文采用所有灰度的中间值作为阈值进行二值化，二值化结果如图4（a）所示。

图4 图像二值化Fig.4 Image binaryzation

从图4（a）可以看出，在小尺度运动模糊图像的“去噪”频谱中采用灰度中间值作为阈值进行二值化不会造成整个图像的噪点现象，但是由于中心十字亮线的存在会对方向估计产生影响。对于大小为M×N像素的图像，M、N为奇数时，十字亮线出现在（M＋1）／2行和（N＋1）／2列；M、N 为偶数时，十字亮线出现在（M／2）＋1行和（N／2）＋1列，对图像的中心亮线去除可以直接令亮线所在行和列的数值为0［4］。进一步分析图4可以发现，除了中心十字亮线的干扰之外，由于小尺度运动模糊图像频谱的亮线短，频谱中心亮斑的存在极易造成方向鉴别误差，因此，必须分析中心亮斑的形成原因并考虑去除。对清晰Lena图像进行二次傅里叶变换，可以得到二次频谱如图5所示。

图5 清晰标准Lena图像频谱图Fig.5 Fourier spectrogram of Lena image

从图5可以看出，在清晰标准Lena图像进行二次傅里叶变换后的二次频谱中同样存在中心亮斑，因此，中心亮斑不包含方向特征的原始图像信息，在运动模糊的方向鉴别中会产生干扰作用。本文将得到的运动模糊图像的二值化图像减去原始清晰图像中的亮斑，以进一步使方向特征更加明显，结果如图6（a）所示。

对二值频谱进行进一步分析，我们发现，若按照中心十字亮线的坐标对频谱进行分块，对角线所在2个象限的亮点个数相同，且方向特征所在的2个象限亮点个数一定大于其他2个象限的亮点数。因此，计算4个象限所在块的亮点个数，留下亮点数多的2个象限，令亮点个数少的2个象限都为0，可得如图6（b）所示的频谱分块去除后的二值化图像。

图6 二值图像的去干扰结果Fig.6 Results of binary image for eliminating interference

从图6可以看出，经过去除中心光斑和分块去除处理后的二值化图像方向特征明显得到提高，可以对其进行方向特征提取。

2.3 方向特征提取算法设计

图像投影即图像在某一方向上的线性积分，要精确提取出二值图像中的方向特征，可以将其投影到过中心点的直线上，积分最大的一条直线X′即与所求方向相垂直。因此，根据（3）式所示的垂直关系即可得到小尺度运动模糊图像的模糊方向估计值：

式中：α表示直线X′的角度；θ表示运动模糊方向参数。

投影结果如图7所示（L＝3，θ＝10°）。

图7 方向特征提取结果Fig.7 Results of direction extraction

从图7可以看出，积分最大的直线X′角度为100°，由此可得，运动模糊方向为10°。

3 实验验证

3.1 Lena标准测试图像的算法仿真验证

为了验证本文算法的有效性，将Lena测试图像在不同模糊小尺度和不同模糊角度下进行模糊，并将本文算法与经典算法进行对比分析，对比实验结果如表1。

从仿真结果可以看出，本文方法进行方向鉴别时具有良好的精度和准确性，相比其他文献算法，本文算法更能满足小尺度运动模糊图像模糊方向鉴别的要求。

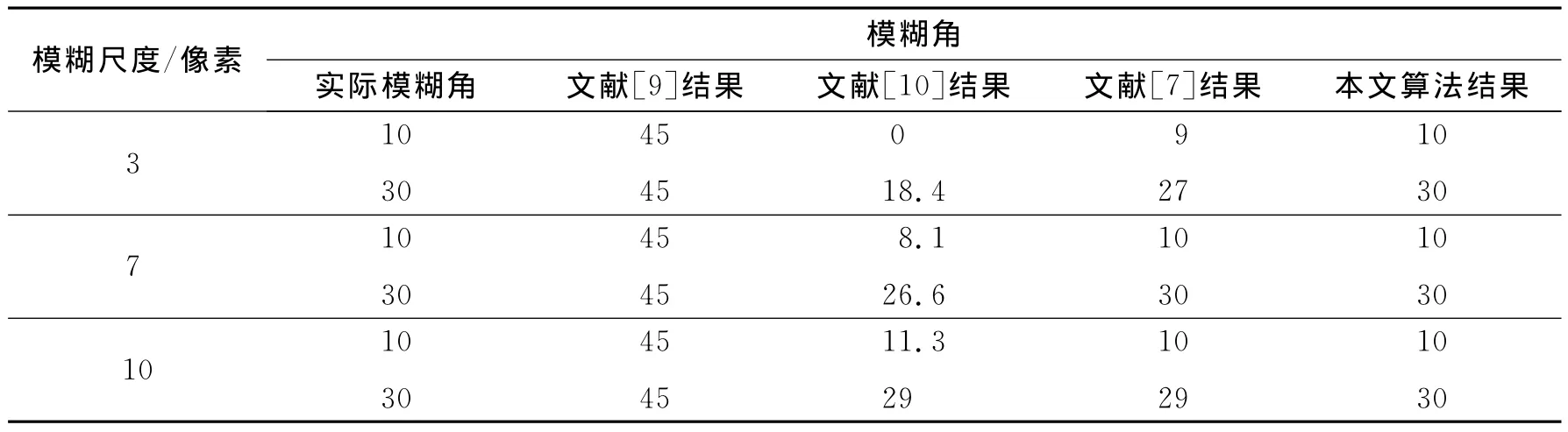
表1 Lena图像不同方法下的实验结果Table 1 Results of direction estimation by 4 algorithms

为了更直观地观察本文算法的优点，将本文算法与各经典算法鉴别出的模糊方向值通过维纳滤波对图像进行复原，复原结果如图8所示。

图8 Lena图像维纳滤波复原结果（L＝3，θ＝30°）Fig.8 Results of Lena image restoration（L＝3，θ＝30°）

从图8可以看出，根据文献［11］、［12］鉴别出的参数复原图像几乎无法辨识，文献［9］的复原结果与本文算法相比仍有一定差距。

3.2 实拍复杂图像的算法仿真验证

为了克服仿真图像的单一性，进一步说明本文算法的有效性，现选取实拍复杂图像“海滩”和“城市”进行仿真分析。分别对其进行不同方向的小尺度运动模糊，具体模糊参数如图9所示。

图9 实拍复杂小尺度运动模糊图像Fig.9 Real complicated small－scale motion blurred image

从图9可以看出，相较于大尺度的运动模糊图像，当实拍复杂图像出现小尺度运动模糊情况时，人们凭肉眼也是很难估计出模糊方向。本文算法针对现有算法产生鉴别误差的原因，着重解决频谱产生干扰从而不易于检测的问题，使得频谱方向特征更加明显更利于鉴别，如图10所示。

图10 本文算法处理前后频谱对比图Fig.10 Comparison of Fourier spectrograms

从图10可以看出，对于复杂图像来说，本文算法处理后的频谱方向特征更加明显，取得了较好的效果。最后通过方向特征提取证实了本文算法的有效性，如图11所示。

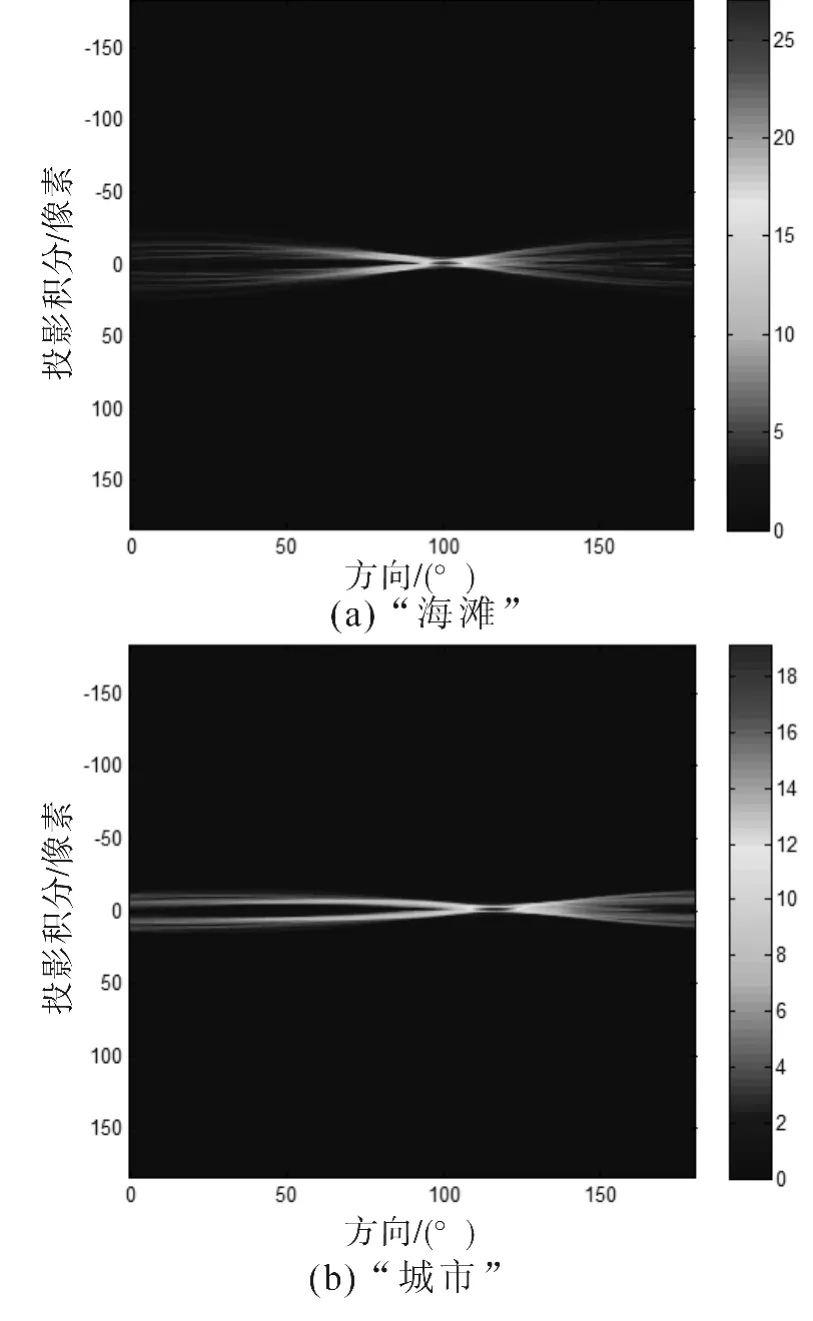
图11 实拍复杂图像模糊方向鉴别结果Fig.11 Results of direction estimation for real complicated image

从图11的实验结果可以看出，本文算法对小尺度运动模糊下的实际复杂图像同样具有很好的模糊方向鉴别效果。

4 结束语

本文从运动模糊图像及其方向鉴别产生误差的成因出发，通过对运动模糊图像的频谱进行分析和处理，在小尺度运动模糊情况下实现了模糊方向的精确鉴别。该算法主要有如下特点：1）利用中值滤波器对二次傅里叶频谱进行“去噪”，在提高方向特征的同时便于图像进行二值化时阈值的选取；2）在去除中心十字亮线的基础上创造性地提出了去除中心亮斑，进一步使得频谱方向特征更加明显，其有效性通过实验得到了验证。虽然文中提出的算法具有一定的局限性，但是为小尺度运动模糊图像提供了一种模糊方向精确鉴别的新思路。

［1］ Zhang Yujin.Image engineering［M］.3rd ed.Beijing：Tsinghua University Press，2012.

章毓晋.图像工程［M］.3版.北京：清华大学出版社，2012.

［2］ Moghaddam M E，Jamzad M.Motion blur identification in noisy images using mathematical models and statistical measures［J］.Pattern Recognition，2007，40（7）：1946－1957.

［3］ Moghaddam M E，Jamzad M.Linear motion blur identification in noisy images using fuzzy sets［C］.US：IEEE，2005：862－866

［4］ Liang Min，Zhu Hong.Motion blur parameter estimation based on correlation coefficient analysis with reference image［J］.Chinese Journal of Scientific Instruments，2014，35（1）：88－96.

梁敏，朱虹.基于参考图相关系数分析的运动模糊参数估计［J］.仪器仪表学报，2014，35（1）：88－96.

［5］ Wu Haibin，Liu Chao，Yu Xiaoyang，et al.Motion blurred direction estimation for video monitor image［J］.Chinese Journal of Liquid Crystals and Display，2014，29（4）：580－585.

吴海滨，刘超，于晓洋，等.视频监控图像的运动模糊方向估计［J］.液晶与显示，2014，29（4）：580－585.

［6］ Guo Hongwei，Fu Bo，Tian Yimin，et al.Deterioration parameter estimation and restoration of photo－graphic motion－blurred image［J］.Laser ＆Infrared，2013，43（5）：559－564.

郭红伟，付波，田益民，等.实拍运动模糊图像的退化参数估计与复原［J］.激光与红外，2013，43（5）：559－564.

［7］ Liang Wanyu，Sun Quansen，Xia Deshen.Identification of the motion blur direction using spectral property［J］.Journal of Image and Graphics，2011，16（7）：1164－4469.

梁宛玉，孙权森，夏德深.利用频谱特性鉴别运动模糊方向［J］.中国图象图形学报，2011，16（7）：1164－4469.

［8］ Lu Xiaodong.Restoration of motion－blurred image by generalized method based on SVD［J］.Journal of Applied Optics，2013，34（1）：90－94.

鲁晓东.基于奇异值分解的运动模糊图像广义逆恢复方法［J］.应用光学，2013，34（1）：90－94.

［9］ Guo Hongwei，Tian Yimin，Fu Bo.Accurate detection of the motion blurred direction based on twice fourier spectrum［J］.Journal of Yunnan University of Nationalities：Natural Sciences Edition，2012，21（4）：301－304.

郭红伟，田益民，付波.基于二次傅里叶频谱的运动模糊方向精确检测［J］.云南民族大学学报：自然科学版，2012，21（4）：301－304.

［10］Kong Yongqi，Lu Min，Pan Zhigeng.Motion blur direction detection based on pre－processing of spectrum image［J］.Journal of Image and Graphics，2013，18（6）：637－646.

孔勇奇，卢敏，潘志庚.频谱预处理模糊运动方向鉴别的改进算法［J］.中国图象图形学报，2013，18（6）：637－646.

［11］Deng Zefeng，Xiong Youlun.Identification of motionblur direction based on frequency－domain algorithm［J］.Opto－Electronic Engineering，2007，34（10）：98－101.

邓泽峰，熊有伦.基于频域方法的运动模糊方向识别［J］.光电工程，2007，34（10）：98－101.

［12］Xie Wei，Qin Qianqing.Estimating blur parameters of point spread function of motion－blurred image based on cepstrum［J］.Geomatics and Information Science of Wuhan University，2008，33（2）：128－131.

谢伟，秦前清.基于倒频谱的运动模糊图像PSF参数估计［J］.武汉大学学报：信息科学版，2008，33（2）：128－131.