瑞奇－康芒式大口径平面镜面形数据处理方法对比研究

朱 硕，张晓辉

引言

在光学检测领域中大口径平面镜作为标准器具常用作光学系统的自准，对其本身的面形精度具有很高的要求［1－5］。随着平面镜制作口径越来越大，干涉测量法无法对口径过大的平面镜进行直接检测，使高精度大口径平面镜检测成为难题［6］。瑞奇－康芒法作为在大口径平面镜检测中一种常用的检测方法［7－13］，测试时需要一块面形精度较高的球面镜作为参考镜，检测方法直观、易于实现，且具有较好的稳定性。在国外，有关瑞奇－康芒检测法的研究已经相对成熟并能达到较高的测试精度［14－15］；近些年来，针对大口径平面镜检测问题，国内一些研究机构已相继开始使用瑞奇－康芒法对大口径平面镜进行检测，但检测精度仍有待提高［16］。本文根据瑞奇－康芒检测原理，针对面形结果计算精度问题，提出利用几何坐标转换关系对系统波像差进行恢复的方法，两角度检测后结合最小二乘法分离出调整误差影响，从而得到被检平面镜的面形。通过仿真证明此方法的有效性并给出计算精度，与目前常使用的影响矩阵算法的计算结果作对比，证明坐标转换法在一定程度上可以提高计算结果精度，使结果更接近平面镜面形的真实情况。最后通过实验对一块口径为100 mm的平面镜进行检测，分别采用2种数据处理方法对所测波前进行面形恢复并与干涉仪直接检测检测结果对比，结果证明对同一组测试数据处理后，通过坐标转换关系计算得到的面形精度更高，验证了仿真结果的正确性，为提高瑞奇－康芒法的检测结果精度提供了理论依据。

1 算法原理分析

图1为瑞奇－康芒法检测原理图。干涉仪发出的准直光束经过标准镜头成为发散光出射，镜头焦点恰好位于标准球面镜的曲率中心处，将被检平面镜以一定的角度θ斜插入到光路中，光束经过平面镜反射到标准球面镜，再经标准球面镜反射沿原光路返回与干涉仪内部的参考光束发生干涉，最终根据测得系统波像差分析并计算得到平面镜的面形误差［17－18］。

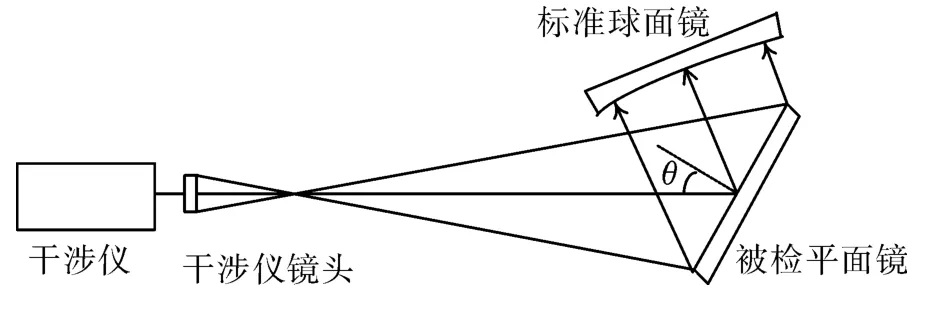
图1 瑞奇－康芒法检测原理图Fig.1 Principle diagram of Ritchey－Common test

图2 给出了准直光束在不同入射角度情况下，系统波像差与面形误差的关系［19］。根据测试原理可知，瑞奇－康芒法在检测时测试光束2次经过被检平面镜，测得系统波像差中包含4倍的平面镜面形误差，并且由于平面镜以一定角度插入在发散光路中，光束实际经过的光程差为s×cosθ，故测得的波像差W＝4s×cosθ，但不同于准直光束的是由于测试光束是以发散的球面波形式入射到平面镜上，导致平面镜上任一点入射角的大小都不同，如对测得系统波像差仍进行单一角度的转换会使计算得到的面形误差存在一定误差。

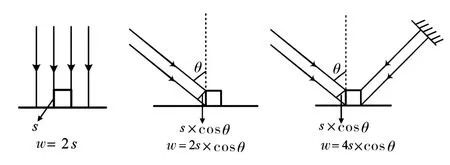
图2 面形误差与波像差关系Fig.2 Relationship between surface error and wave fronts

目前常用于瑞奇－康芒检测面形恢复的方法是利用Zernike多项式表示面形误差以及系统波像差的具体形式，根据面形误差中的各误差项对波像差的贡献，在近似的条件下推导出二者之间的影响函数［17］，利用此影响函数以及多角度测得的系统波像差数据求出面形误差的Zernike系数，进而根据（1）式拟合出平面镜的面形：

式中：ai为Zernike多项式的系数；Zn为Zernike多项式基底。

本文在以上研究的基础上，根据瑞奇－康芒检测原理，分析系统光瞳面坐标系与平面镜坐标系之间的相对位置关系，如图3所示。

图3 坐标关系图Fig.3 Relationship between coordinates

利用几何方法直接推导二者的转换关系：

式中：xs、ys表示被检平面镜镜面坐标；xp、yp表示系统光瞳面坐标；两坐标系间的夹角与瑞奇角θ大小相同；d为干涉仪镜头焦点到被检平面镜中心的距离。平面镜面形误差S（xs，ys）引起了系统波像差W（xp，yp）的变化，经过2次反射后，二者的关系可表示为

式中I表示任意入射角。同样利用几何位置关系来表示I：

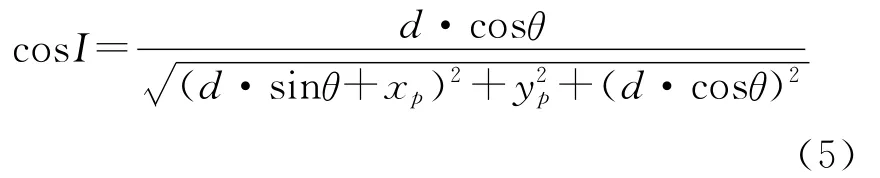
根据（4）式和（5）式即可建立平面面形误差与系统波像差之间的幅值转换函数。

利用以上转换公式对测得波像差进行处理即可对测得压缩波前进行恢复展开从而得到被检平面镜的面形误差。

由于测试过程中使用一块面形精度较高的球面镜作为参考镜，光路调整过程中会引入离焦项误差，并且被检平面镜斜插入在发散测试光路中，平面镜自身像散与大曲率半径引入的影响混叠在一起，单次检测无法区分，需要进行多角度检测以得到最终的面形结果。利用两角度检测数据结合最小二乘法可以分离出调整误差影响，以得到最终的面形结果。

2 仿真

为进一步分析此算法的计算精度，在Zemax软件中搭建瑞奇－康芒仿真测试光路对检测进行模拟。在软件中以点光源模拟干涉仪的发散光束，仿真光路图如图4所示。

图4 仿真测试光路Fig.4 Simulation test path

利用Zernike多项式给出一个假设的平面镜面形：将假设平面镜插入到仿真光路中，光线追迹后得到系统波像差，利用坐标关系转换法对其进行展开，计算平面镜的面形，将结果与假设的原始面形作对比并分析计算精度。再使用影响矩阵法对测试波前进行计算，对比2种方法的计算精度，为实际测试提供理论依据。

假设平面镜的面形情况如图5所示，其峰谷值PV为0.047 4λ，均方根误差RMS值为0.007 4λ，将瑞奇角设定为30°、45°进行光线追迹后得到两角度下的系统波像差，使用几何坐标转换法对波像差数据进行展开处理，计算出的面形结果其PV值为0.046 4λ、RSM 值为0.007 3λ，图6（a）为计算得到的平面面形图，理论上算法的PV检测精度达到0.001λ、RMS检测精度达到0.000 1λ。同时也对波像差数据使用影响矩阵法来分析，计算得到的面形结果其PV值为0.036 3λ、RMS值为0.005 8λ，面形情况如图6（b）所示，比较结果可知，坐标转换法可以更好的恢复出平面镜的面形情况且精度较高。

图5 假设平面镜面形误差Fig.5 Supposed flat surface error

通过仿真分析可知，相比影响矩阵法，几何坐标关系转换法可以更好地对测得系统波像差进行面形恢复。此方法可以将测得波前中数据每一采样点精确地对应到其镜面坐标位置上，并且按其相应的入射角度进行幅值转换，不但避免了近似关系下推导引入的误差，同时也避免了使用Zernike多项式拟合带来的误差。并且在实际检测中，影响矩阵法在数据处理时平面镜面形误差对离焦项的贡献与光路调整过程中引入的离焦误差无法区分，需要舍弃离焦项再进行拟合，而坐标转换法可以利用两角度检测在最终结果中分离出由光路调整误差带来的误差，一定程度上使瑞奇－康芒检测法的精度得到了提高，可使最终计算得到的面形结果更为真实地反映出平面镜的面形情况，更利于瑞奇－康芒检测数据分析。

图6 仿真面形结果Fig.6 Surface result of simulation

3 实验与结果分析

实验通过对一块口径为100mm的平面镜进行检测来进一步证明理论分析的正确性。选择一块球面反射镜作为参考镜，其口径为280mm，曲率半径为1 172mm，实验平台布局如图7所示。

图7 实验平台布局Fig.7 Experimental layout

根据目前实验室检测条件，选择抗震能力较好的4D动态干涉仪进行瑞奇－康芒实验。实验首先对标准球面镜进行标定，得到球面镜的面形误差以便在后续处理时予以剔除；第二步搭建瑞奇－康芒检测光路，在瑞奇角角度为24°状态下对平面镜进行检测，微调光路直到干涉仪所测得的波像差稳定开始记录数据；在获得第一组波前数据后旋转平面镜至40°位置，调整光路完成两角度检测。需要注意的是，在改变瑞奇角的过程中必须确保干涉标准镜头焦点到平面镜中心的距离保持不变，从而保证两角度检测时系统光瞳面坐标系与平面镜坐标系间对应位置的一致性与正确性，检测时可利用高精度转台配合完成角度的旋转。

对两角度下测得数据分别使用2种方法进行分析解算，图8给出了坐标转换法计算平面镜面形误差的最终结果，面形的PV值为0.149λ，RMS值为0.017 7λ，表1给出了使用最小二乘法分离出的离焦项误差系数。

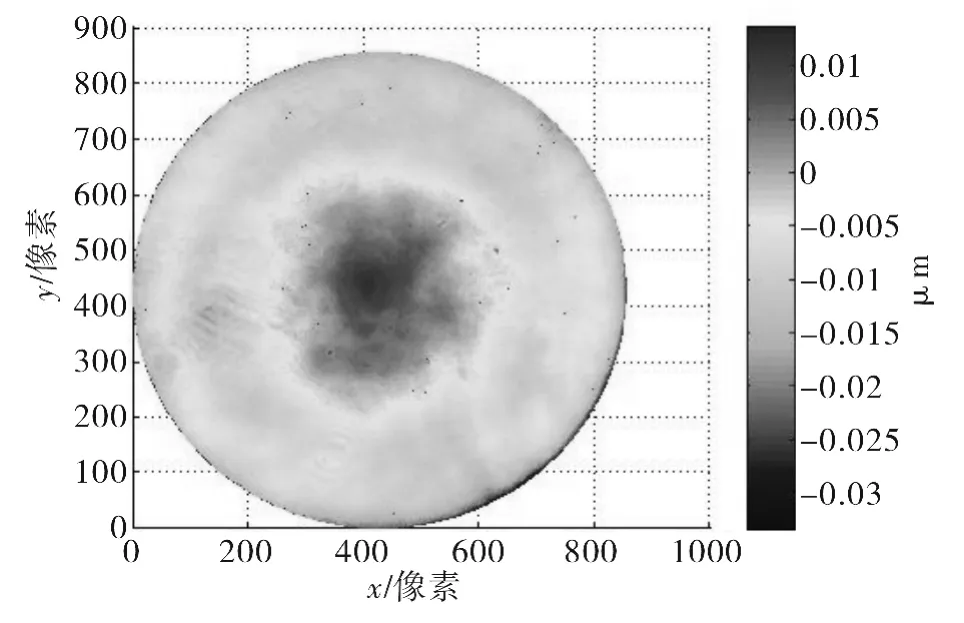
图8 坐标转换法结果Fig.8 Result of coordinate transforming（PV＝0.149，RMS＝0.0177λ）

表1 离焦项系数Table 1 Coefficients of defocus

使用影响矩阵法对测得数据进行处理，计算得到的面形PV值为0.136λ，RMS值为0.014λ，面形结果如图9所示。

由于4D干涉仪提供的准直光束的口径较小，不能对被检平面镜直接进行检测，故选择ZYGO干涉仪直接对平面镜检测，得到的面形情况如图10所示，PV值为0.162λ，RMS值为0.022λ。为便于比较，表2列出了3次结果的PV及RMS值。

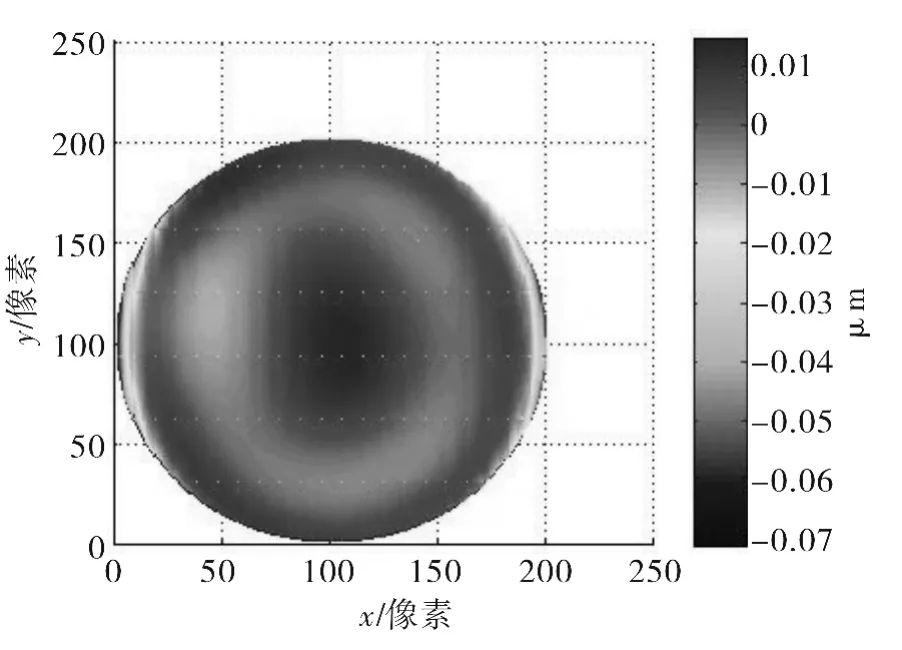
图9 影响矩阵法结果Fig.9 Result of impact matrix（PV＝0.136λ，RMS＝0.014λ）

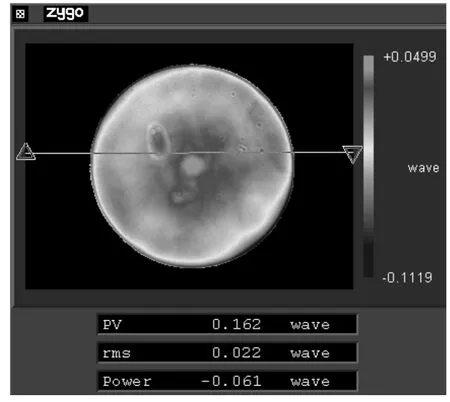
图10 Zygo干涉仪测得平面镜面形Fig.10 Flat surface figure measured by Zygo

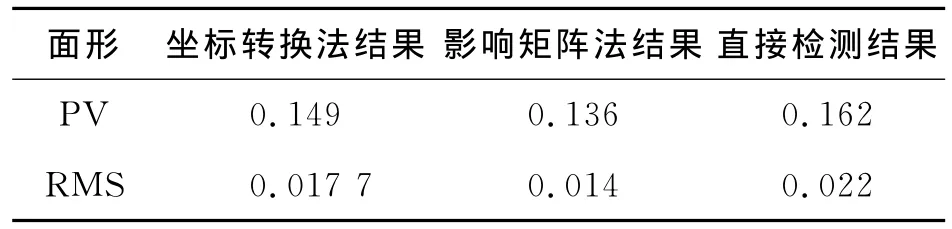
表2 3次结果比较 λTable 2 Comparison of results by 3 methods

分别将2种面形恢复方法的分析计算结果与直接检测得到的结果作比对，可以看到坐标转换法计算出的面形更为接近实际面形情况，峰谷值PV实际检测精度优于1／20λ，均方根值RMS实际检测精度优于1／100λ，且相对影响矩阵法PV精度提高了0.013λ，RMS精度提高了0.003 7λ。坐标转换法在数据后续处理时，在将面形数据从椭圆域展开成圆域的过程中，需要对弧矢方向的数据作插值处理，一定程度上会造成对高频误差的平滑，但由于平面镜在加工过程中高频误差较小，故对最终计算结果的影响不大，可以忽略其影响。实验结果证明了坐标转换法的计算精度较高，在实际测试时可以分离出系统的调整误差，使检测结果更为真实地反映出真实的平面镜面形情况，更有利于高精度瑞奇－康芒检测。为提高瑞奇－康芒法检测精度提供理论依据。实验过程中为减小环境和人为因素的影响，必须进行多次测量取稳定的检测数据进行计算。

4 结论

本文针对使用瑞奇－康芒法检测大口径平面中数据处理问题，着重介绍了利用几何坐标转换关系计算出平面镜面形误差的方法，详细介绍了其原理及计算方法。通过仿真模拟实际测试光路，分析了此方法的计算精度，并给出了与影响矩阵法结果的对比结果。通过实验对一小口径平面镜检测，分别使用2种面形恢复方法计算得到平面镜面形数据，对比干涉仪直接检测的结果，坐标转换法的PV实际检测精度优于1／20λ，RMS实际检测精度优于1／100λ，实现了高精度检测，证明了仿真分析的正确性，也为提高瑞奇－康芒检测法精度提供了依据，在实验中选择坐标转换法对测得波前数据进行分析解算可以使结果更为真实准确地反映出被检平面镜的面形情况。

［1］ Julius Y，Burge J H.Analysis of a scanning pentaprism system for measurements of large flat mirrors［J］.Applied Optics，2007，46（35）：8466－8474.

［2］ Zhu Shuo，Zhang Xiaohui.Eliminating alignment error and analysizing Ritchey angle accuracy in Ritchey－Common test［J］.Optics Communications，2013，311：368－374

［3］ Ma Chuntao，Luo Hongxin，Wang Jie，et al.Surface error measurement of plane mirrors based on oblique incidence ［J］.Laser ＆ Optoelectronics Progress，2011，48（7）：071201.

马春桃，罗红心，王劼，等.斜入射法检测平面反射镜的面形误差［J］.激光与光电子学进展，2011，48（7）：071201.

［4］ Zhu Shuo，Zhang Xiaohui.Application of error detaching to Ritchey－Common test for flat mirrors［J］.Optics and Precision Engineering，2014，22（1）：7－12.

朱硕，张晓辉.误差分离技术在平面镜瑞奇－康芒法检测中的应用［J］.光学精密工程，2014，22（1）：7－12.

［5］ Bai Manshe，Li Pan，Zhang Jinkuan，et al.Improvement on nonuniformity for sphere mirrors with large radius of curvature［J］.Optics and Precision Engineering，2013，21（3）：554－560.

白满社，李攀，张晋宽，等.大曲率半径球面反射镜球面误差的改善［J］.光学精密工程，2013，21（3）：554－560.

［6］ Zheng Ligong.Testing of precise mirror based on subaperture stitching［J］.Journal of Applied Optics，2014，35（1）：85－89.

郑立功.基于子孔径拼接法测量高精度反射镜［J］.应用光学，2014，35（1）：85－89.

［7］ Zhu Shuo，Zhang Xiaohui.Analysis and verification for accuracy of Ritchey angle in flat mirror test［J］.Acta Optica Sinica，2013，33（6）：0612001.

朱硕，张晓辉.Ritchey角精度对平面镜检测的影响的分析与验证［J］.光学学报，2013，33（6）：0612001.

［8］ Chao Geping，Yang Pengli，Yang Zijian，et al.Adjustment method for testing conica aspheric optical elements based on wavefront contour map［J］.Journal of Applied Optics，2014，35（4）：652－655.

晁格平，杨朋利，杨子建，等.二次非球面经检测中基于波前等高线图的调整方法［J］.应用光学，2014，35（4）：652－655.

［9］ Zhu Shuo，Zhang Xiaohui.Study on high precision Ritchey－Common test and analysis of test distance influence ［J］.Acta Optica Sinica，2014，34（1）：0112001.

朱硕，张晓辉.高精度瑞奇－康芒检测法研究及测试距离 精 度 影 响 分 析 ［J］.光 学 学 报，2014，34（1）：0112001.

［10］Chen Fengjun，Yin Shaohun，Yu Jianwu，et al.An ultra－precision on machine measurement method of aspheric surface［J］.Laser ＆ Optoelectronics Progress.2012，49（7）：071203

陈逢军，尹韶辉，余剑武，等.一种超精密非球面在位测量 方 法 ［J］.激 光 与 光 电 子 学 进 展，2012，49（7）：071203

［11］Xuan Bin，Song Shumei.Influence of polarization direction nonorthogonality on precision of polarization phase shifting interferometry［J］.Optics and Precision Engineering，2013，21（12）：3001－3007.

宣斌，宋淑梅.偏振正交性对偏振相移干涉检测精度的 影 响 ［J］.光 学 精 密 工 程，2013，21（12）：3001－3007

［12］Ren Huan，Ma Li，Liu Xu，et al.Optical element test with multiple surface interference ［J］.Optics and Precision Engineering，2013，21（5）：1144－1150.

任寰，马力，刘旭，等.多表面干涉情况下光学元件面形 检 测 技 术 ［J］.光 学 精 密 工 程，2013，21（5）：1144－1150.

［13］Wang Zongyang，Wang Bin，Wu Yuanhao，et al.Calibration of non－common path static aberrations by using phase diversity technology［J］.Acta Optica Sinica，2012，37（7）：0701007.

汪宗洋，王斌，吴元昊，等.利用相位差异技术校准非共 光 路 静 态 像 差 ［J］.光 学 学 报，2012，37（7）：0701007.

［14］Chai Liqun，Shi Qikai，Wei Xiaohong，et al.Testing of root mean square of mid－spatial－frequency wavefront for large flat［J］.Chinese J.Lasers，2012，39（1）：0108003.

柴立群，石琦凯，魏小红，等.大口径平板中频波前均方 根 的 测 量 误 差 ［J］.中 国 激 光，2012，39（1）：0108003.

［15］Wang Bin，Wang Zongyang，Wu yuanhao，et al.Calibration of no－common path aberration in AO system by multi－channel phase－diversity［J］.Optics and Precision Engineering，2013，21（7）：1683－1692.

王斌，汪宗洋，吴元昊，等.利用多通道相位差异波前探测法检测自适应光学系统非共光路像差［J］.光学精密工程，2013，21（7）：1683－1692.

［16］Shu K L.Ray－trace anlysis and data reduction method for the Ritchey－Common test［J］.Applied Optics，1983，22（12）：1879－1886.

［17］Han S，Novak E，Schuring M. Application of Ritchey－Common test in large flat measurements［J］.SPIE，2001，4399（67）：131－136.

［18］Yuan Lyujun，Xing Na.Study on the Ritchey－Common interferometry for large plano optics［J］.Optical Technique，2007，33（5）：737－744..

袁吕军，邢娜.大口径光学平面镜瑞奇－康芒检测技术的研究［J］.光学技术，2007，33（5）：737－744.

［19］Tian Xiuyun，Wu Shibin，Wu Fan，et al.A data progress method in Ritchey－Common test［J］.Opto－Electronic Engineering，2004，31（1）：23－31.

田秀云，吴时彬，伍凡.等.瑞奇－康芒法中的一种数据处理方法［J］.光电工程，2004，31（1）：23－31