基于0-1线性规划的近地天体望远镜巡天调度优化∗
2015-06-27歆1昊1赵海斌1彬1炎1
王 歆1,2† 陆 昊1,3 赵海斌1,3 李 彬1,3 夏 炎1,3
(1中国科学院紫金山天文台南京210008) (2中国科学院空间目标与碎片观测重点实验室南京210008) (3中国科学院行星科学重点实验室南京210008)
基于0-1线性规划的近地天体望远镜巡天调度优化∗
王 歆1,2† 陆 昊1,3 赵海斌1,3 李 彬1,3 夏 炎1,3
(1中国科学院紫金山天文台南京210008) (2中国科学院空间目标与碎片观测重点实验室南京210008) (3中国科学院行星科学重点实验室南京210008)
针对近地天体望远镜巡天观测的特点,将调度优化问题转化为约束优化问题.通过引入0-1变量,实现了目标函数和约束条件的线性化表达,建立了0-1线性规划模型.优化调度中不仅考虑了观测价值的最大化,同时也考虑了观测资源的消耗.仿真表明,通过模型优化可简便地考虑更多的因素,充分发挥望远镜运行效率.
望远镜,方法:实测
1 引言
近地天体望远镜是目前我国在国际小行星预警网络(IAWN,International Asteroid Warning Network)中唯一的观测设备,采用了1.0 m/1.2 m口径的施密特光学系统,焦距1.8 m,视场3.14◦,主要开展大视场小行星巡天观测.由于极其出色的观测探测能力,近地天体望远镜投入运行以来也开展了许多其他类型的观测[1-3],并建立了观测图像数据库[4-5].其中大多数观测仅仅需要对特定源在比较宽松的时间范围内进行少数几次观测的任务,都安排在巡天任务间隙共同执行.为了提高探测能力,近地天体望远镜的探测终端升级成了目前最大的单芯片的CCD相机,尽管读出速度提高,但由于靶面增大,读出时间仍然变长.相机在图像采集中采用了连续工作模式,一次采集将连续获取多张图像,而终止和启动这样的采集过程都有额外的较长时间消耗.如何更好地调度近地天体望远镜的巡天观测以及和其他观测需求有机结合在一起,减少不必要的观测时间消耗就成为提高近地天体望远镜运行效率的关键问题.
长期以来在观测实践中,为了节约观测时间,近地天体望远镜利用相机读出时间进行望远镜摆位,并升级了控制软件系统,实现了全自动的调度[6],但巡天观测计划由于主要依赖工作人员的定性选择,缺少定量的理论依据,因此无法实现计划的自动输入.为了简化,目前总是选择相邻并可循环连接的天区.同时为了满足一些其他观测需求,观测中常常是终止常规的巡天计划,用巡天组间间隙,人工重新将望远镜摆位到指定天区后拍摄图像,完成观测任务后再重新启动后续巡天计划.执行时间完全依据观测员经验和习惯.
合理的优化调度是望远镜良好运行的前提条件,特别是随着设备自动化程度的提高,对调度优化也提出了新的要求,采用数学方法对观测计划调度进行优化也成为许多国际上大型望远镜的常规研究内容.
Palomar Transient Factory(PTF)采用了自动队列调度系统(Automated Queue Scheduler),采用邻视策略(Shortsighted strategy)进行观测的实时调度,由于不是优化整晚的观测队列,这种方法比较适用于对后续观测条件以及观测资源消耗关注度较小的设备[7].
而对于哈勃空间望远镜(HST,Hubble Space Telescope)和甚大望远镜(VLT,Very Large Telescope)等设备,它们不仅需要最大程度地获得天文观测数据,还需要考虑观测资源的消耗,因此将调度问题考虑为一个具有多重约束的复杂调度问题.HST首先采用了基于神经网络的优化算法[8],Space Telescope Science Institute在为HST的优化调度软件开发中,形成了一个框架系统—Spike planning and scheduling software,并成功应用于Chandra Advanced X-Ray Astrophysics Facility(AXAF)、Space InfraRed Telescope Facility(SIRTF)、VLT、VLBI Space Observatory Program(VSOP)以及Subaru Telescope等[9-16].
开源的RTS2(Remote Telescope System 2nd Edition)系统原先采用一个简单的价值函数对计划进行优选,后也改进为采用遗传算法进行优化调度[17].
望远镜调度优化被认为是一个NP-Hard(Non-deterministic Polynomial Hard)问题,因此启发式算法在望远镜调度中有很广泛的应用,例如邻域搜索法(Neighbourhood Search Method)和遗传算法[18].
望远镜调度优化势必与其运行的具体情况密切相关,上述工作也都针对具体应用的观测模式和设备运行状态进行了特别的研究.本文针对近地天体望远镜巡天观测模式下的调度优化问题做了初步探索,采用0-1线性规划刻画了巡天调度的数学模型,实现了适合近地天体望远镜运行实际情况的优化策略,模型求解则可通过成熟的整数线性规划算法以及软件包实现.
2 巡天模式
近地天体望远镜根据望远镜的视场将全天以天球赤道坐标(α,δ)为索引分为4 772个固定天区,巡天观测时对于任何观测时间选择观测源所在的固定天区实施观测.
对于小行星巡天,与传统观测略有区别,它需要通过对同一个天区的一定间隔的重复观测来识别移动的小行星.近地天体望远镜目前采用了3次重复天区的方式,即对同一个天区以固定时间间隔重复观测3次,通过3幅观测图像的比对找出候选小行星.观测中,在得到一张观测图像后,利用CCD相机的读出时间,望远镜摆位到下一个观测天区,对于目前采用的CCD相机,望远镜摆位时间必须在26 s内,因此相邻时间的观测天区跨度不能太大.
为了便于人工排列计划,目前多数采用了1组约20个天区的观测方式,曝光时间60 s,对20个天区循环3次,为了使得相邻观测天区跨度符合摆位要求,只能选择相互循环相连的整片天区.
事实上,每个天区的观测价值不同,每个天区地平方位和高度坐标(A,h)随时间在变化,导致观测效果不同,以及不同相位角区域理想的重复时间也不同.这些因素如完全依赖人工调度,难以考虑,从而使得设备的效率发挥尚不充分.
对于只需对特定源进行观测的任务,由于观测时间以及重复性没有特殊要求.目前近地天体望远镜在巡天组间进行这类观测,主要是为了不破坏人工排列的巡天计划,但从设备运行角度,总希望这样的观测和巡天计划可有机融合,在巡天过程中能直接执行这些观测,从而减少望远镜附加移动和CCD相机的重新启动,节约观测时间.
3 数学模型
观测调度是一个典型的约束优化问题,满足各类条件情况下,如何获得最佳的观测方案.通过上述分析,近地天体望远镜巡天任务和传统天文观测任务有所区别,对于一个天区,需要完成若干次观测,科学价值只有完成全部图像采集后才能发挥;考虑到CCD相机的工作模式,相邻天区的距离必须小于读出时间内望远镜的移动距离,因此望远镜的移动距离不能作为优化变量考虑,而必须是对可行域的约束.
对于观测计划而言,首要考虑的是观测科学价值最大化.各个天区的观测价值一般用适应度( fi tness)来表示,适应度越大表示观测价值越高,换言之在调度中被优先实施.各天区的适应度和许多因素相关,包括:观测时的地平高度、与黄道面的距离、天光背景情况(主要和月光相关)、历史观测情况以及观测任务的重要程度等,这些量中有些是天区固有的属性,有些是与时间相关的,天区的适应度取值可根据经验和具体观测需求确定,但时间确定后,天区适应度都是确定的.
定义总的天区集合为S={si,i=1,2,···,N},观测的时间窗口集合为T={ti,i= 1,2,···,NT},共NT个窗口,ti按时间顺序排列.各窗口的开始时刻定义为W(t),是已知的.适应度为天区s和时间窗口t的函数F(t,s).对于巡天观测而言,需要确定的是每个可观测的时间窗口观测哪个天区.巡天优化调度转换为指派问题,可直观表达为图1的形式.图中每1列对应1个时间窗口,每1行对应1个天区,每个格子中的数值代表该格子的价值.调度就是在图中按照一定规则选格子,每列至多选择1个格子,每行选择3个格子或者不选择;相邻两列选择的格子距离不能太远,每行选择的各个格子之间距离也要满足一定要求,例如图1中灰色格子就构成了1个可行的调度方案.这样的可行选择有很多,评判选择优劣的标准是选中的格子数值和最大,优化目标就是找到最优的调度方案.
将上述问题转换为数学模型,为了便于建立线性条件,定义决策变量dtofk∈{0,1},其中t∈T,o∈S,f∈S,k∈{1,2,···,NK}.k用于表示小行星巡天轮次,NK是需要的轮次,对于近地天体望远镜NK=3.例如d1361=1表示在t1时间窗口观测s3天区,是该天区的首轮观测,下一个时间窗口,即t2观测s6.
令当晚巡天的候选天区集合为Ss,非巡天观测任务所需天区为So,Ss∩So=∅.同时引入天区集合S0,该集合中只有一个元素即0号天区s0,这个天区是一个虚拟的天区,观测s0表示该时段空闲.对于调度而言总的可观测天区为Sa=So∪Ss∪S0.
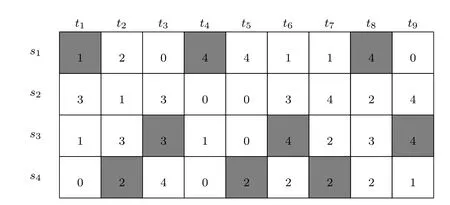
图1 调度问题的示意图Fig.1 The sketch of the scheduling problem
根据上述变量定义,可以建立巡天调度的数学模型,目标函数为最大化观测总适应度:

根据前面分析的巡天观测模式逐一建立约束条件.由于引入了虚拟的s0天区,每个时间窗口必须观测1个天区,有:

其中s.t.为subject to的缩写,表示该式为约束条件.此外,决策变量中包含了下一个时间窗口的观测天区,必须约束:

其中Sub表示取下标,t′是按时间顺序t的下一个元素.对于巡天天区在每个轮次至多观测1次,有:

巡天天区只有观测NK次才能发挥有效作用,安排少几次则没有意义,因此要么安排NK次,或者完全不安排,有:
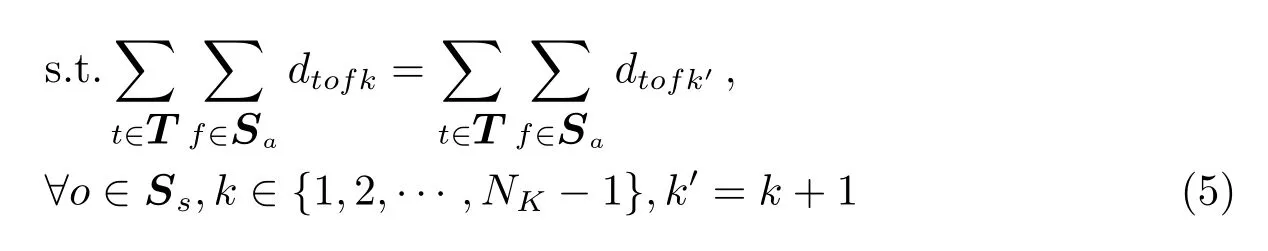
NK轮巡天中后面的轮次必须在前面轮次之后观测,有:
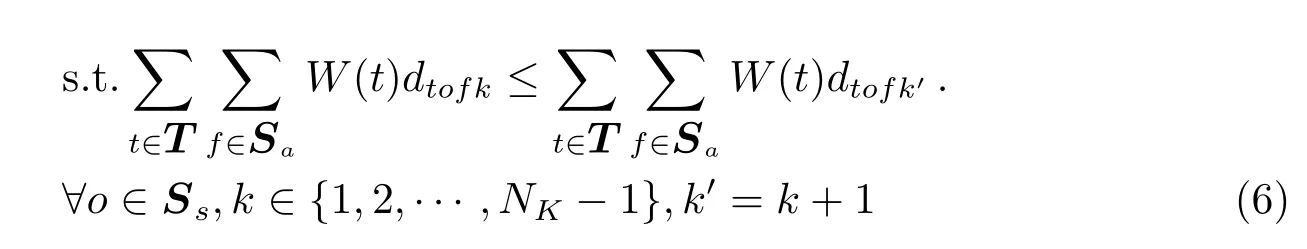
考虑到对于巡天天区重复间隔时间有一定要求,时间太短移动目标不足以区分,对于每个天区,令重复时间必须在[(L(s),U(s)],s∈Ss,上述约束条件(6)式可直接变为:

和
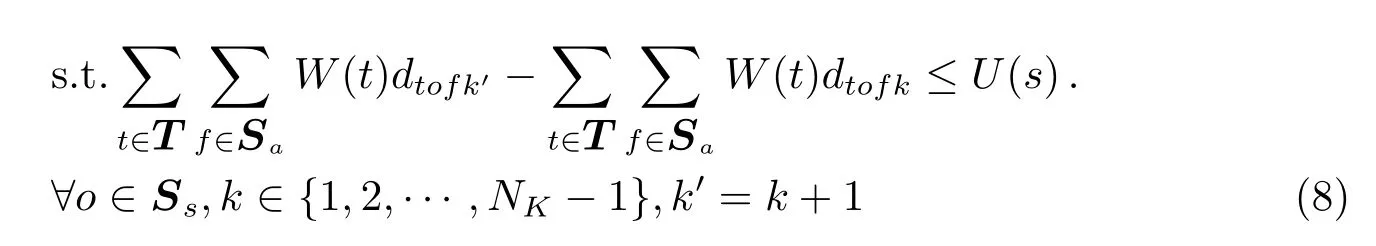
至此,关于巡天天区的约束条件均已建立.对于其他天区,没有轮次问题,约束:

以及非巡天天区一般限制观测不超过约定上限M(o),有:

由于望远镜运动速度有限,相邻两次观测的天区跨度不能太大,定义L(so,sf)为两个天区之间的距离,so∈S,sf∈S,显然有L(so,sf)=L(sf,so).根据望远镜移动速度和相机读出时间可以求得相邻天区的最大间隔Lm.
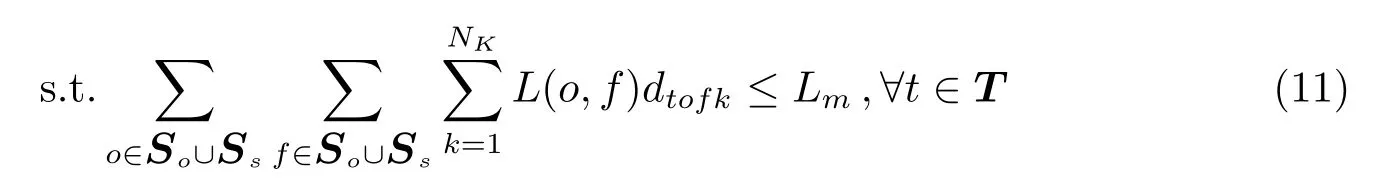
特别约定s0和任意天区都是可以往返的,因此上述约束条件对s0并无限制.最后为了保持一致性,约束最后时刻观测的下一个观测天区为s0:

至此已给出了所有的约束条件,最大化(1)式即可得到观测适应度最好的观测方案.
在获得观测适应度最好的观测方案后,可进一步优化得到望远镜移动距离最小的观测方案,此时将(1)式作为约束条件,不难得到新的目标函数:

近地天体望远镜巡天观测已全部转换为数学模型,模型中较全面地考虑了各种因素,特别是一些在人工排列中难以考虑从而简化的因素,都被完整地考虑进模型.在观测实践中总会遇到对时间有一定要求的观测需求,通过对dtofk的约束很容易将这类需求引入模型之中.事实上只需要对F(t,s)取值合理也可达到同样目的,例如对于不能够实施观测的时间–天区对,可设置其对应的适应度F<F(t,s0),这样上述模型不需任何变化即可满足需求.
从所有的数学条件不难看出,所有的条件均为线性条件,没有决策变量的高阶项,因此可行域是凸的,便于大规模问题的求解.同时决策变量d∈{0,1},通过0-1变量的使用,将望远镜在相邻时间窗口的移动距离等非线性量都转化为了线性表达.因此本文建立的模型为0-1线性规划模型.
4 仿真试验
为了验证本文提出的模型,进行了仿真试验.考虑3轮巡天,共有连续的30个时间窗口.候选天区为:S0={0},So={1},Ss={2,4,6,8,10,12,14,16};对各天区F取了定值,F(t,0)=−1,F(t,1)=1,∀t;F(t,s)=2,∀t,s∈Ss;时间窗口为等长,取W(ti)=i;仿真中只有一个非巡天天区,取M(1)=2.各天区之间的距离L取值见表1.表中m,n分别表示起止天区编号.L(0,0)<L(0,n),n̸=0以及L(0,0)̸=0是为了在优化过程中可以使得s0天区尽可能连续,减少间断次数.优化中约定望远镜只能摆位到距离为1的天区, LM=1.
由于采用了0-1线性规划模型,模型可通过标准的数学规划语言表达,并通过求解软件求解.在仿真试验中,采用GLPK1http://www.gnu.org/software/glpk/(GNU Linear Programming Kit)软件包定义的MathProg语言编写了模型,并通过该软件包将模型转化为线性规划标准的MPS (Mathematical Programming System)格式.求解采用了Gurobi2http://www.gurobi.com(版本5.6.3)软件的免费学术版.
巡天的重复时间间隔在仿真中做了统一约定,模拟了两种情况.当重复时间比较宽松,[(L(s),U(s)]取[7,15]时,经两步优化得到的观测适应度为46,最短路径为55,具体结果为:
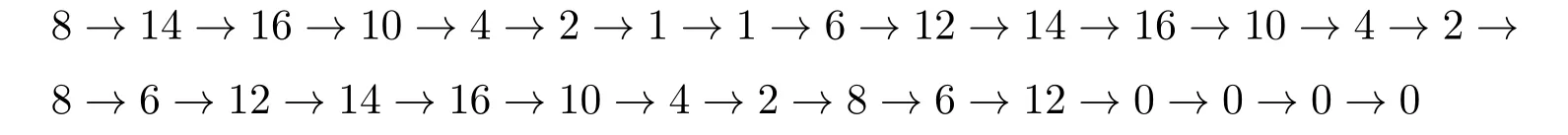
经直观验证可知该结果为最优结果,符合预期.说明模型表达正确有效.优化结果中s0都连续排列在最后,这和之前L取值时的考虑完全吻合.

表1 各天区的距离表Table 1 The distances between each two sky areas
当重复时间选取较小,[(L(s),U(s)]取[7,9]时,优化结果为:

观测适应度仍为46,最短路径也为55.
仿真表明通过数学模型表达,当一些条件发生变化时,只需要对模型参数进行调整即可继续求得最优解,十分便捷,也适合自动处理.当约束条件发生变化时,通过数学求解往往可以克服各种约束条件的限制,使得调度效益可以和弱约束甚至无约束情况下保持一致.
5 讨论与展望
本文将近地天体望远镜巡天调度处理为约束优化问题,通过选择决策变量为0-1变量,使得约束条件和目标函数均为线性条件.0-1线性规划模型作为一种经典的模型,有许多成熟的求解算法和软件包,极大地方便了在望远镜运行中的应用.优化着眼于观测的整体情况,符合小行星巡天的任务特点.
本文只是对近地天体望远镜巡天策略进行了初步探索,近地天体望远镜还开展了多样的观测任务,例如小行星的光变曲线观测、反银心方向巡天等,如何将这些观测需求和巡天任务相互融合还有待进一步探索.
此外,随着时域天文的兴起,ToO(Target of Opportunity)观测在近地天体望远镜观测中越来越多,和巡天观测快速融合实现实时调度也是重要的方向.
采用数学方法进行望远镜调度,不仅有利于充分利用望远镜观测资源,发挥设备效率,也能更好地支持无人值守的全自动观测.随着望远镜机电能力的提高,以及观测任务的多样性与实时性要求的提高,优化调度势必发挥更大的作用.
参考文献
[1]李彬,赵海斌.天文学报,2012,53:240
[2]Li B,Zhao H B.ChA&A,2013,37:97
[3]叶嘉晖,赵海斌,李彬.天文学报,2015,56:243
[4]王歆.天文学报,2013,54:382
[5]Wang X.ChA&A,2014,38:211
[6]王歆,赵海斌,夏炎,等.天文学报,2015,56:178
[7]Cenko S B,Fox D B,Moon D S,et al.PASP,2006,118:1396
[8]Josnston M D,Adorf H M.Computers and Operations Research,1992,19:209
[9]Johnston M,Miller G.Intelligent Scheduling.San Francisco:Morgan-Kaufmann,1994:391
[10]Miller G,Bose A.ASP Conference Series,adass V,1996,101:467
[11]Giuliano M.ASP Conference Series,adass VII,1998,145:271
[12]Foor L Z,Asson D J.Spike:A Dynamic Interactive Component in a Human-Computer Long-range Planning System.3rd International NASA Workshop on Planning and Scheduling for Space,Houston, October 27-29,2002
[13]Chavan A M,Giannone G,Silva D,et al.ASP Conference Series,adass VII,1998,145:255
[14]Giannone G,Chavan A M,Silva D R,et al.ASP Conference Series,adass IX,2000,216:111
[15]Meier D L,Fomalont E B.AdSpR,2000,26:629
[16]Sasaki T,Kosugi G,Kawai J A,et al.Proceedings of SPIE,2000,4009:350
[17]Kubanek P.Genetic Algorithm for Robotic Telescope Scheduling.Granada:Universidad de Granada, 2008
[18]G´omez de Castro A I,Y´a˜nez J.A&A,2003,403:357
0-1 Linear Programming for CNEOST Survey Scheduling
WANG Xin1,2LU Hao1,3ZHAO Hai-bin1,3LI Bin1,3XIA Yan1,3
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008) (2 Key Laboratory for Space Object and Debris Observation,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008) (3 Key Laboratory of Planetary Sciences,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)
Survey scheduling of the CNEOST(China Near Earth Object Survey Telescope)is studied as a constrained optimization problem.Employing the 0-1 variables,both the objective functions and constraints in the model are linearized,and the 0-1 linear programming model is constructed.For the optimization,not only the scienti fi c productivity of the observation but also the consume of observing resources are considered.Simulations show that with the model,more factors can be dealt with conveniently,and the observation efficiency will be improved.
telescopes,methods:observational
P111;
:A
2014-11-21收到原稿,2014-12-30收到修改稿
∗国家自然科学基金项目(11373072,11273067)、江苏省自然科学基金项目(BK2011890)和小行星基金会资助
†wangxin@pmo.ac.cn
10.15940/j.cnki.0001-5245.2015.04.009
