小质量裸奇异星的r模不稳定性研究∗

皮春梅 杨书华

(1湖北第二师范学院物理与机电工程学院武汉430205) (2华中师范大学天体物理研究所武汉430079)

小质量裸奇异星的r模不稳定性研究∗

皮春梅1杨书华2†

(1湖北第二师范学院物理与机电工程学院武汉430205) (2华中师范大学天体物理研究所武汉430079)

在修正袋模型参数所允许的范围内构建奇异星模型,研究了小质量裸奇异星的r模不稳定窗口.结果表明随着星体质量的减小,r模不稳定性所约束的奇异星极限旋转频率增大;根据参数选取的不同,质量在约0.1～0.2 M⊙以下的裸奇异星都可以解释观测到的转速最快的716 Hz脉冲星数据.

恒星:中子,恒星:振荡,恒星：转动,恒星:小质量,恒星:内部

1 引言

自1998年提出以来,致密星演化过程中可能存在的r模不稳定性(引力波不稳定性的一种)已经被广泛研究[1−2].致密星r模不稳定性的研究具有两方面的重要意义:一方面,可以通过r模不稳定性所限制的极限旋转来解释脉冲星周期[3−6];另一方面,致密星发生r模不稳定时的引力波辐射可能被新一代引力波探测器观测到[7].另外,致密星发生r模不稳定时,星体内部的粘滞耗散加热对星体热演化具有重要影响.例如,r模不稳定耗散加热结束后星体的冷却过程,可以很好地解释观测到的Cas A超新星遗迹内中子星的快速冷却现象[8−9].

根据Witten的奇异夸克物质假设[10],致密星可能是由u、d、s 3味夸克物质所组成的奇异星,而不是由中子物质所组成的中子星.有很多工作研究了奇异星的r模不稳定性,并与脉冲星观测进行对比,试图区分奇异星和中子星,如文献[3]和[11-16].

然而,之前r模不稳定性相关研究一般是针对1.4 M⊙左右的奇异星,本文将研究小质量裸奇异星的r模不稳定性.需要指出的是,文献[17]中也简要研究了小质量裸奇异星的r模不稳定性,并通过定性分析得到与本文类似的结论,即:星体质量越小,引力波辐射率越低,r模不稳定性所约束的极限旋转频率越大.而本文中除了对r模不稳定机制相关时标的仔细计算外,还通过已观测到的最大质量脉冲星PSR J1614-2230 (M=(1.97±0.04)M⊙)[18]和PSR J0348+0432(M=(2.01±0.04)M⊙)[19]限制奇异夸克物质物态方程的参数,并且用小质量裸奇异星的r模不稳定窗口解释观测到的转速最快的716 Hz脉冲星数据[20].

到目前为止已经有一些天文观测支持小质量奇异星的存在[17,21−23],但尚未得到最终确认.另外,在起源问题上,小质量裸奇异星可能很难在大质量星的超新星爆发中形成,但是已经有研究指出它们可以由白矮星吸积物质并坍缩而形成[17,24].

本文的工作仅局限于研究裸奇异星情形,带壳层奇异星的相关研究较为复杂,我们将在后续工作中进行.另外,我们的研究也不涉及夸克集团星[25−26],因为夸克集团星的内部物质是刚性的,星体不会发生r模不稳定.

2 奇异夸克物质物态方程与奇异星

对奇异夸克物质,我们采用唯象的修正袋模型[27−29].该模型中通过引入耦合系数αS考虑了强相互作用一阶微扰修正,u夸克和d夸克为零质量粒子,s夸克的质量作为自由参数.u、d、s夸克和电子的巨热力学势分别为其中mi和µi分别为粒子i的质量和化学势,f(µs,ms)≡是重正化常数,文中取σ=300 MeV.

关于物态方程中自由参数组(s夸克质量ms,袋常数B,强相互作用耦合常数αS)的选取,我们沿用文献[16]和[30]的做法.首先,u,d,s夸克和电子所组成的奇异夸克物质的结合能比56Fe的(～930 MeV)低.其次,仅仅由u夸克和d夸克组成的两味夸克物质的结合能比铁原子核的结合能(考虑表面能的修正后一般取为934 MeV)高.最后,所选取的参数组还要保证该物态方程代入计算星体结构的Oppenheimer-Volkof公式后,所计算出的星体序列的最大质量大于已观测到的脉冲星最大质量,即PSR J1614-2230 (M=(1.97±0.04)M⊙)[18]和PSR J0348+0432(M=(2.01±0.04)M⊙)[19].文献[16]中图1的左图和右图中分别给出了ms=100 MeV和ms=200 MeV时,B1/4和αS同时满足以上3个要求的参数空间.

本文在研究小质量裸奇异星的r模不稳定窗口时,将参照文献[16]的图1选取具有代表性的、同时符合上述3个要求的状态方程参数组进行研究.具体地,我们将选取ms=100 MeV,B1/4=140 MeV和ms=200 MeV,B1/4=135 MeV两种情形进行讨论;前一种情形下我们将分别考虑αS=0.2,αS=0.4和αS=0.6,后一种情形下则只考虑αS=0.4和αS=0.6(从文献[16]的图1中可以看出,ms=200 MeV,B1/4=135 MeV时,若取αS=0.2,则无法满足上文所提到的第2个状态方程限制条件).

为了对下文所探讨的不同质量裸奇异星有一些直观的概念,我们在图1中给出了裸奇异星的质量-半径关系.值得注意的是,图1中我们只给出αS=0.4情形,因为对于相同的ms和B1/4,改变αS时,质量-半径关系曲线几乎都是重合的.

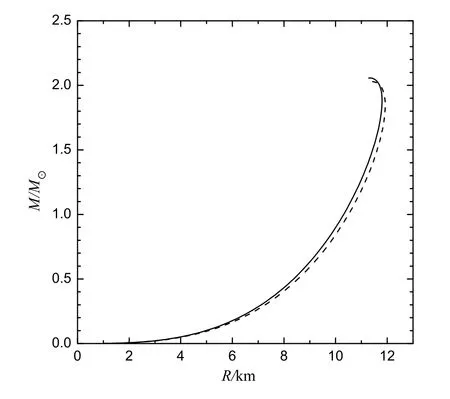
图1 奇异星的质量-半径关系图.图中实线对应于ms=100 MeV,B1/4=140 MeV,αS=0.4;虚线对应于ms=200 MeV,B1/4=135 MeV,αS=0.4.Fig.1The mass-radius relation of strange stars.The solid line is for ms=100 MeV,B1/4=140 MeV, and αS=0.4,and the dashed line is for ms=200 MeV,B1/4=135 MeV,and αS=0.4.

3 小质量裸奇异星的r模不稳定窗口

1998年，Andersson[1]以及Friedman和Morsink[2]最先指出,不考虑内部的耗散机制时,所有的转动致密星中r模都是不稳定的.如果考虑星体内部的粘滞耗散机制,星体是否发生r模不稳定则取决于引力波驱动效应与粘滞耗散的衰减效应之间的竞争.奇异星的r模不稳定窗口由以下不等式所决定:

其中τGW是引力波驱动时标,τη和τζ分别是剪切粘滞和体粘滞所导致的粘滞耗散时标.所谓r模不稳定窗口,即是在T-Ω(T是星体温度,Ω是星体自转频率)图上满足(5)式的区域.在这些区域内,星体是不能够稳定存在的,因为此时引力波对r模的驱动效应大于粘滞耗散的衰减效应,引力波辐射将带走大量的星体角动量,使得星体转速急剧下降,直到星体脱离该窗口.

引力波驱动时标为[31]

其中ρ是密度(单位为g·cm−3).本文中,将只考虑起决定作用的l=2和m=2的r模.

剪切粘滞耗散时标为[31]

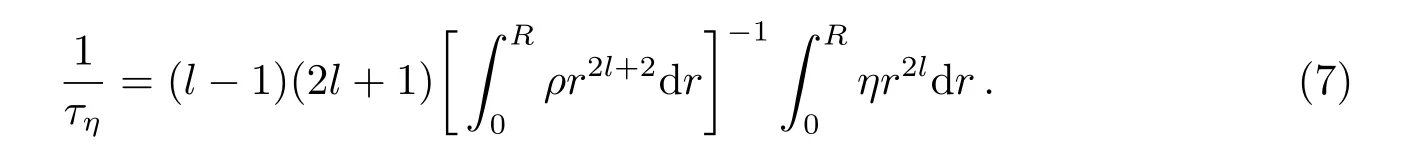
剪切粘滞主要来自于夸克-夸克散射[32],对于温度T远小于化学势µ的情形,有[3]

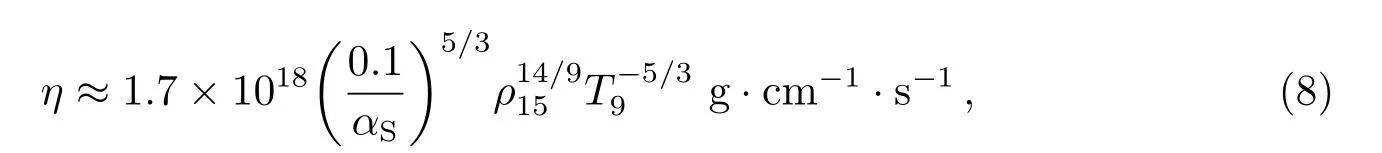
其中T9≡T/(109K),ρ15≡ρ/(1015g·cm−3).

体粘滞耗散时标为[33−36]

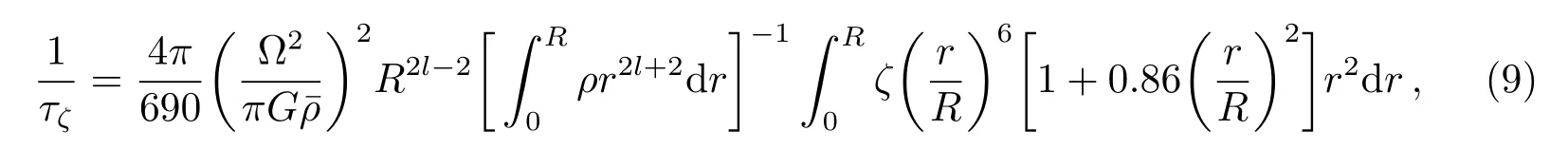
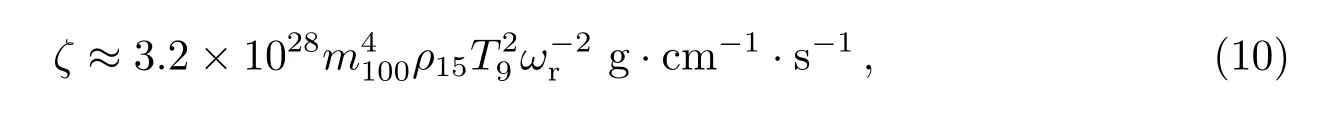
其中,ωr=2mΩ/[l(l+1)]是r模的频率(对于起决定作用的m=l=2的r模,ωr=Ω), m100是以100 MeV为单位的s夸克质量,其他参量都采用cgs单位制.

4 结果与讨论

在确定的奇异夸克物质物态方程参数组(ms,B1/4,αS)下,通过对(5)式的数值计算,可得到奇异星的r模不稳定窗口.

图2给出了ms=100 MeV,B1/4=140 MeV,αS=0.4时小质量裸奇异星的r模不稳定窗口.我们发现,随着星体质量的减小,星体的r模不稳定窗口上移,窗口下边缘轮廓线的最低点所对应的极限旋转频率增大.图中,M=0.132 M⊙所对应虚线的最低频率为716 Hz(这是目前发现的最高转速的脉冲星),这意味着所有M ＜0.132 M⊙的奇异星都不会在716 Hz旋转频率下发生r模不稳定.与图2的做法类似,可以找到ms=100 MeV,B1/4=140 MeV情况下,当αS=0.2时,716 Hz所限制的奇异星质量为M=0.164 M⊙;而当αS=0.6时,所限制的奇异星质量为M=0.117 M⊙(为保持图像的简洁明了,图2中并未画出这两条曲线).

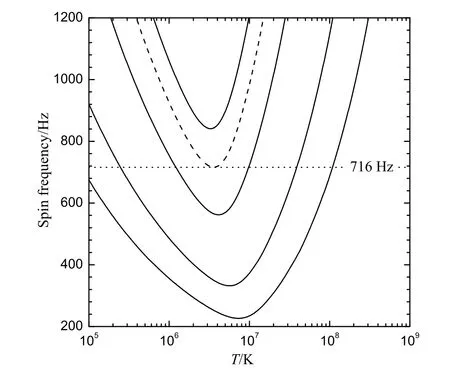
图2 小质量裸奇异星的r模不稳定窗口，物态方程的参数取为ms=100 MeV,B1/4=140 MeV,αS=0.4.图中实线从上到下依次对应于星体质量M=0.1 M⊙,0.2 M⊙,0.5 M⊙,1.0 M⊙,虚线对应于M=0.132 M⊙.另外,图中点线标出的转动频率为716 Hz.Fig.2The r-mode instability window of low-mass bare strange stars with the parameters of the equation of state taken as ms=100 MeV,B1/4=140 MeV,and αS=0.4.The solid line is for M=0.1 M⊙,0.2 M⊙,0.5 M⊙,and 1.0 M⊙from top to bottom,respectively;and the dashed line is for M=0.132 M⊙. Moreover,the dotted line is for the spin frequency marked as 716 Hz.

图3给出了ms=200 MeV,B1/4=135 MeV,αS=0.4时小质量裸奇异星的r模不稳定窗口.与图2相比,图3中的星体不稳定窗口整体都向左上方偏移.此时,716 Hz脉冲星所限制的奇异星质量为M=0.197 M⊙.与图3的做法类似,可找到ms=200 MeV, B1/4=135 MeV,αS=0.6时,716 Hz所限制的奇异星质量为M=0.175 M⊙.我们没有研究ms=200 MeV,B1/4=135 MeV,αS=0.2时的奇异星r模不稳定窗口,因为此时由u夸克和d夸克组成的两味夸克物质的结合能比铁原子核的结合能低,不符合在第2节中提到的选取状态方程参数的条件.

图3 与图2类似,但是物态方程的参数取为ms=200 MeV,B1/4=135 MeV,αS=0.4.另外,与图2不同,图中虚线对应于M=0.197 M⊙.Fig.3 Similar to Fig.2,but with the parameters of the equation of state taken as ms=200 MeV, B1/4=135 MeV,and αS=0.4.What’s more,it is di ff erent from Fig.2 that the dashed line in this fi gure is for M=0.197 M⊙.

5 结论

研究了小质量裸奇异星的r模不稳定窗口,发现随着星体质量的减小,r模不稳定性所允许的奇异星极限旋转频率增大.并且,通过与观测到的转速最快的716 Hz脉冲星对比,发现根据奇异夸克物质状态方程参数选取的不同,质量在约0.1～0.2 M⊙以下的裸奇异星都可以具有这样快的极限旋转频率.

[1]Andersson N.ApJ,1998,502:708

[2]Friedman J L,Morsink S M.ApJ,1998,502:714

[3]Madsen J.PhRvL,1998,81:3311

[4]Andersson N,Kokkotas K D,Stergioulas N.ApJ,1999,516:307

[5]潘娜娜,杨书华,郑小平.天文学报,2004,45:272

[6]Pan N N,Yang S H,Zheng X P.ChA&A,2005,29:53

[7]Abadie J,Abbott B P,Abbott R,et al.ApJ,2010,722:1504

[8]Yang S H,Zheng X P,Pi C M,et al.MNRAS,2010,403:2007

[9]Yang S H,Pi C M,Zheng X P.ApJ,2011,735:L29

[10]Witten E.PhRvD,1984,30:272

[11]Madsen J.PhRvL,2000,85:10

[12]Andersson N,Jones D I,Kokkotas K D.MNRAS,2002,337:1224

[13]Zheng X P,Yang S H,Li J R.ApJ,2003,585:L135

[14]Haskell B,Degenaar N,Ho W C G.MNRAS,2012,424:93

[15]Alford M G,Schwenzer K.PhRvL,2014,113:1102

[16]Pi C M,Yang S H,Zheng X P.RAA,2015,15:871

[17]Xu R X.MNRAS,2005,356:359

[18]Demorest P,Pennucci T,Ransom S,et al.Nature,2010,467:1081

[19]Antoniadis J,Freire P C C,Wex N,et al.Science,2013,340:448

[20]Hessels J W T,Ransom S M,Stairs I H,et al.Science,2006,311:1901

[21]Drake J J,Marshall H L,Dreizler S.ApJ,2002,572:996

[22]Yue Y L,Cui X H,Xu R X.ApJ,2006,649:L95

[23]Li Z S,Qu Z J,Chen L,et al.ApJ,2015,798:56

[24]Du Y J,Xu R X,Qiao G J,et al.MNRAS,2009,399:1587

[25]Xu R X.ApJ,2003,596:L59

[26]Guo Y J,Lai X Y,Xu R X.ChPhC,2014,38:055101

[27]Alcock C,Farhi E,Olinto A.ApJ,1986,310：261

[28]Weber F.PrPNP,2005,54:193

[29]Na X S,Xu R X,Weber F,et al.PhRvD,2012,86:123016

[30]Weissenborn S,Sagert I,Pagliara G.ApJ,2011,740:L14

[31]Lindblom L,Owen B J,Morsink S M.PhRvL,1998,80:4843

[32]Heiselberg H,Pethick C J.PhRvD,1993,48:2916

[33]Lindblom L,Mendell G,Owen B J.PhRvD,1999,60:064006

[34]Lindblom L,Owen B J.PhRvD,2002,65:063006

[35]Nayyar M,Owen B J.PhRvD,2006,73:084001

[36]Vida˜na I.PhRvC,2012,85:045808

[37]Wang Q D,Lu T.PhLB,1984,148:211

[38]Sawyer R F.PhLB,1989,233:412

[39]Madsen J.PhRvD,1992,46:3290

R-mode Instability of Low-mass Bare Strange Stars

PI Chun-mei1YANG Shu-hua2
(1 Department of Physics and Engineering,Hubei University of Education,Wuhan 430205) (2 Institute of Astrophysics,Huazhong Normal University,Wuhan 430079)

The r-mode instability window of low-mass strange stars is studied using the modi fi ed bag model of strange quark matter and reasonable sets of parameters.The results show that the spin frequency limit of strange stars increases with the decrease of their mass,and the highest observed spin frequency(716 Hz)of pulsars can be explained if the strange star mass is lower than about 0.1-0.2 M⊙,depending on the parameters of the equation of state.

stars:neutron,stars:oscillations,stars:rotation,stars:low-mass,stars: interiors

P145;

:A

2015-01-12收到原稿,2015-01-21收到修改稿

∗国家自然科学基金项目(11447012和11203010)资助†ysh@phy.ccnu.edu.cn

10.15940/j.cnki.0001-5245.2015.04.003