基于对比试验的Q345钢135°矫正法折弯及回弹优化

刘佳灏,杜勇,薛克敏,张恒光,田耀江,姚嘉炜,葛自良

(合肥工业大学材料科学与工程学院,合肥230009)

基于对比试验的Q345钢135°矫正法折弯及回弹优化

刘佳灏,杜勇,薛克敏,张恒光,田耀江,姚嘉炜,葛自良

(合肥工业大学材料科学与工程学院,合肥230009)

目的 针对自由回弹采用的补偿法寻找最优解过程繁杂,结果不稳定这一问题,寻找更为有效的折弯方式。方法 利用Pearson相关系数和灰色系统理论,采用对比实验,以16 mm厚Q345钢为研究对象,选择凸模圆角、摩擦因数及矫正量为变量,回弹角与最大成形力为目标函数,求得工艺参数对回弹角的关联系数。再对优化的参数组合进行有限元模拟验证。结果 矫正法回弹控制效果远远优于自由折弯模具的回弹控制效果。结论 将优化获得的工艺参数进行有限元模拟验证,指导设计、试模,成形质量得到明显提高,对实际生产具有显著的指导意义。

厚板折弯;对比实验;矫正法;回弹角

伴随着制造行业的发展,金属板材塑性成形工艺在飞机制造、汽车制造及其他工程产品中得以应用[1—4]。众多工件的结构连接处选用了焊接作为连接方式[5],但因为焊缝处材料性能比母材差,导致工件整体的性能降低,同时焊接处也是工件中容易损坏的部位[6—7]。如今,一个较好的解决方式是通过金属板料塑性成形中的折弯工艺来提升工件整体性能和生产效率,同时还提高了材料利用率[8—9]。板料折弯工艺不可避免的是材料的回弹问题[10]。针对这一问题,国内外许多学者都做出了研究,如R.Hill提出了板材弯曲回弹分析的理论基础[11],刘克进的薄板翻边成形以及V形、U形弯曲回弹实验,通过遗传算法得出在实际工艺参数和具体模型下的回弹经验公式[12]。西安交通大学的朱东波等人提出了模具回弹误差补偿修正算法,并通过大量实验进行了验证,结果显示在回弹严重的折弯和浅拉深工艺中,运用该模具修正算法,效果较为理想[13]。

近年来,薄板成形中的主要缺陷已有非常详细的研究[14],涉及到开裂、起皱及回弹等众多方面,可是,对厚度在4 mm以上的中厚板,尤其在回弹现象及其影响因素方面,有待进一步研究。文中针对折弯件的影响因素众多,且目前市场常用的自由折弯的工艺方式缺陷较多这一问题,选用自由折弯与矫正法相对比的对比实验及灰色理论相结合的处理方法对折弯工艺进行探究。

1 模具分析及有限元模拟

1.1 自由折弯模具分析

图1为自由折弯件制作实图,自由折弯是目前较为常用的一种折弯工艺,模具造型简单,工艺灵活度高,但是其准度低,而且折弯后回弹严重。

图1 自由折弯Fig.1 Free bending

1.2 自由折弯的有限元模拟

折弯工艺有限元模拟时,需要输入材料的机械性能参数,包括:密度、弹性模量、泊松比、室温下的应力应变值等输入到Abaqus软件中,从而建立起Q345的材料参数和材料模型(图2)。材料的密度为7860 kg/m3、屈服强度为345 MPa、弹性模量为203 GPa及泊松比为0.285。材料选用实体单元划分,采用遵循Hill准则的各向同性塑性模型,选用基于连续介质的实体单元、罚函数接触[15],并采用动态显示算法计算加载过程和静力隐式算法模拟Q345钢材V形回弹过程。分别选取不同板料厚度作为变量,设计计算机模拟内容。

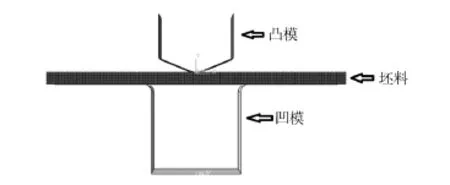
图2 自由折弯有限元模型Fig.2 The finite elementmodel of free bending

对于中厚板折弯成形工艺,无需考察拉裂和起皱缺陷,同时忽略板料厚度变化对回弹产生的影响,只需要考虑如何减少回弹量和最大成形力。因此以成形件回弹量为优化目标,以凸模圆角、下压速度、摩擦因数为变量,网格划分选用均布,具体的实验模拟结果如表1所示。

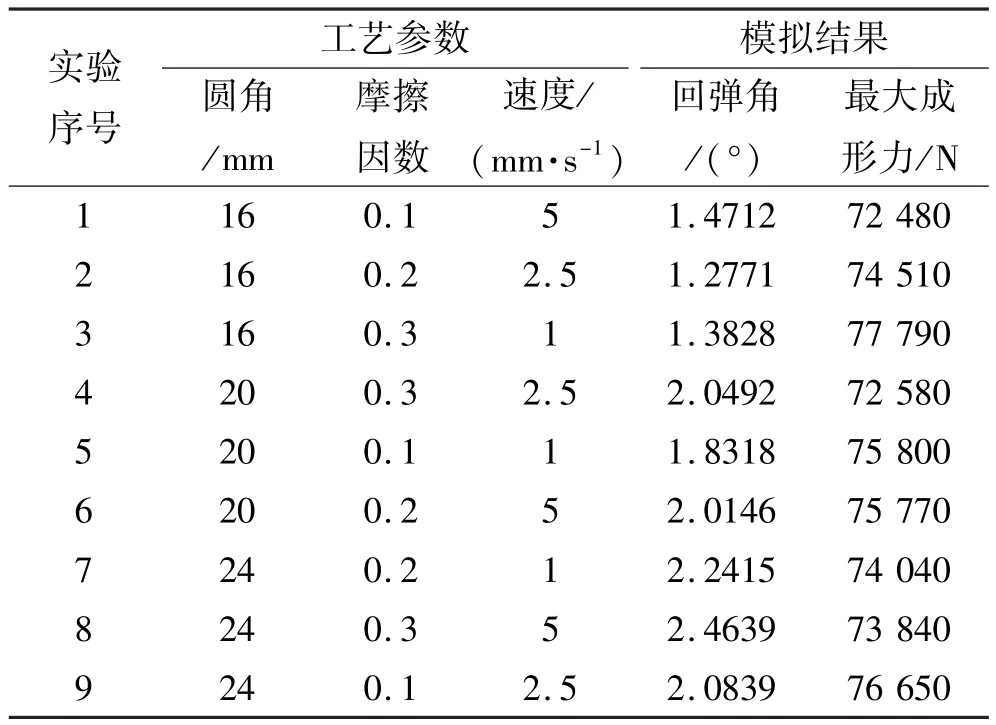
表1 自由折弯的有限元模拟结果Tab le 1 Sim u lated resu lts of free bend ing

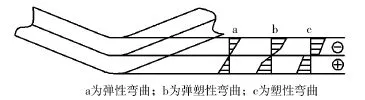
图3 板料弯曲内部应力状态Fig.3 Internal stress state ofmetal bending

由表可知,随着各参数的变化,回弹角也在变化。究其原因,从折弯件应力角度分析如下。

图3显示了板料折弯时主要的三种应力分布,主要探究位置为折弯件的内表面、外表面及中间的应力中性层。其中内、外表面应力最大,呈塑性形变;中部应力最小,呈弹性形变。而折弯件回弹的主要影响因素就是折弯件弹性变形区域的大小。

图4为Q345钢16 mm厚板通过ABAQUS软件模拟得出的在自由折弯条件中凸模下压到最终位置时的应力分布,此时应力分布类型为图3中b类型,且弹性变形区较大,因而此折弯方法回弹角较大。

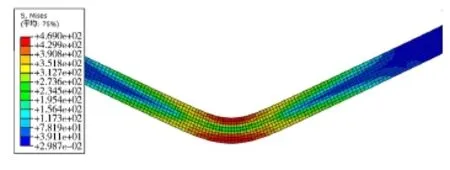
图4 自由弯曲应力分布Fig.4 The bending stress distribution of free bending

1.3 矫正法的模具设计

自由折弯件弹性变形区较大这一问题,较好的解决方式是改进模具,改进效果如图5所示。首先,将凸模与材料变形区接触位置设计成凸起形状,并做圆角处理,使得力集中作用在引起回弹的变形区上,改变弯曲变形区外侧受拉,内侧受压的应力状态使变形区变为三向受压状态,以改变回弹变形性质减小回弹。

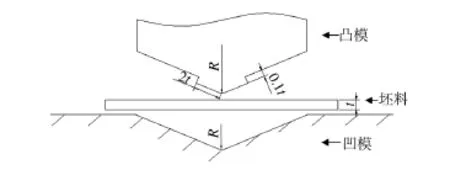
图5 矫正法模型Fig.5 Themodel of orthosismould

1.4 矫正法的有限元模拟

参考自由回弹结果,分别选取凸模圆角、摩擦因数及下压矫正量作为变量。当选取16 mm作为凸模圆角,摩擦因数0.1,矫正压缩2%,得到折弯结果如图6所示。

由图1.6所知,材料的变形区受到了较为集中的应力,近似于图3中的c类型,这使得变形区应力中性层周围的弹性变形部分转变为塑性形变,从而极大可能的减小回弹量。经过合理的参数设计凸模圆角A与矫正量B,通过abaqus模拟,结果如表2所示。

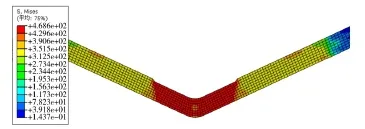
图6 矫正法应力分布Fig.6 Stress distribution by orthosis bending

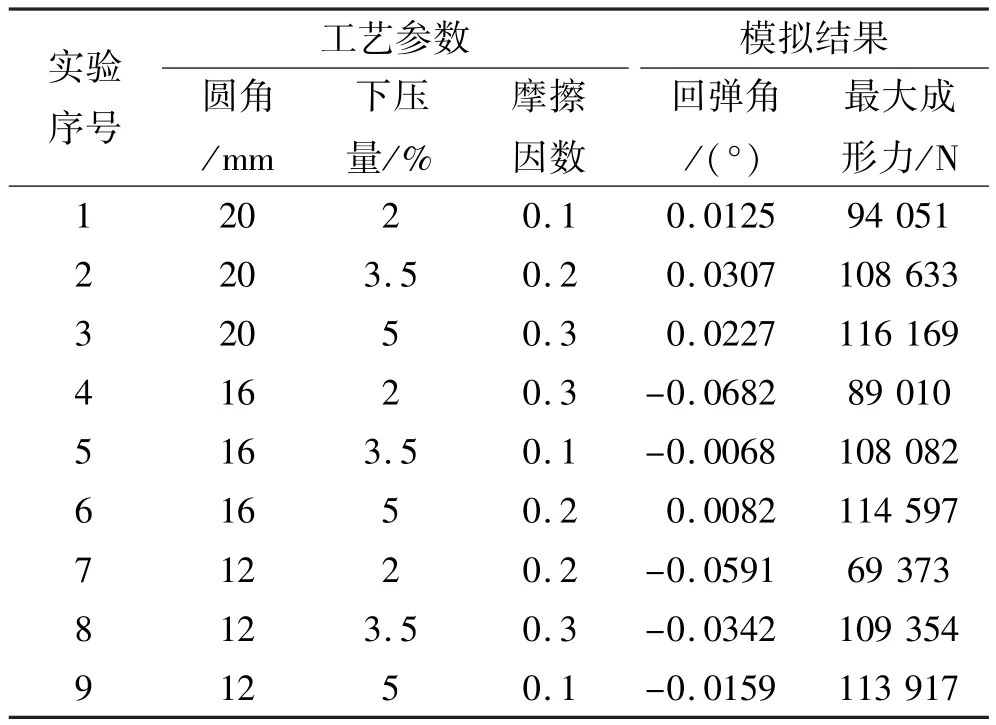
表2 矫正法模拟结果Tab le 2 Sim u lation resu lts of orthosism ethod

由表2可知,矫正法板料的回弹角明显小于自由折弯板料的回弹角,且随着工艺参数的变化而变化;同时,折弯过程中,随着凸模圆角的减小,发生了负回弹的现象,且当凸模圆角R小于板料厚度时,负回弹现象就会产生。

2 数据处理

表2的数据虽可以显示出回弹角及最大成形力会随着工艺参数的变化而变化,但却不能观察出其变化规律,所以需要对数据进行优化处理,来选出最优参数组合。

2.1 Pearson相关系数处理

Pearson相关系数的作用是比较2个数据集合能否在一条线上面或到线的距离,它用来衡量定距变量间的线性关系。如衡量身高和体重、居民储蓄存款和国民收入、高考成绩和高中平时成绩等变量间的线性相关关系。当2个变量都是正态连续变量,而且两者之间呈线性关系时,表现这2个变量之间相关程度用积差相关系数,其计算公式为:

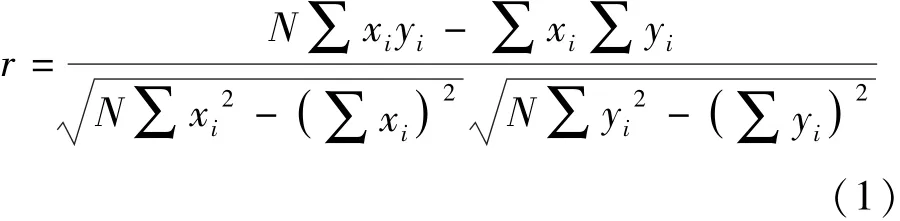
相关系数的大小与绝对值大小有关,相关性越强,相关系数绝对值越接近于1,相关度越强,相关系数越接近于0,相关度越弱。通常情况下,判断变量的相关强度分为:极强相关、强相关、中等程度相关、弱相关、极弱相关或无相关,对应的相关系数值分别为:0.8～1.0,0.6～0.8,0.4～0.6,0.2～0.4,0～0.2。

将数据代入SPSS进行Pearson相关性分析,求得结果如表3所示。

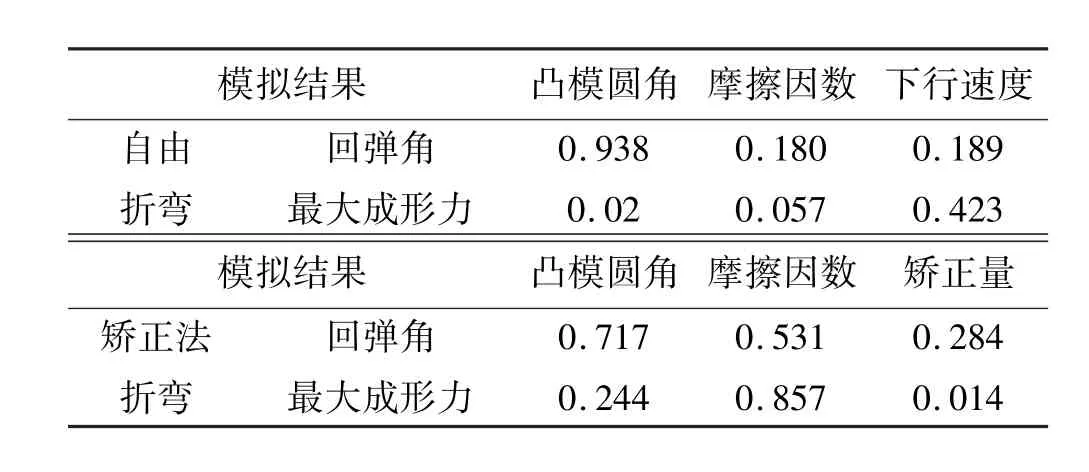
表3 Pearson相关性系数计算结果Tab le 3 The calcu lation resu lts of Pearson related param eters

通过Pearson相关性分析,可知对于自由折弯,凸模圆角影响回弹角最为明显,下行速度影响最大成形力最为明显;而对于矫正法折弯,回弹角的最大影响因素为凸模圆角,而最大成形力的最大影响因素为摩擦因数。

2.2 计算目标函数的灰色关联系数

进行系统分析时,由于系统的复杂性,导致所选取的目标因素的数量级和物理意义可能存在较大的差异。因此在计算灰色关联度前需要通过算子作用,对数据进行无量纲化和正转化处理[16—17]。处理后需要将得到的目标矢量序列设为Xi={xi(k),k=1,2,…,n},i=1,2,…,m,m为目标矢量的个数,基准矢量序列设为X0={x0(k),k=1,2,…,n},则Xi对于X0在第k点的灰色关联系数计算公式如式(2)所示:

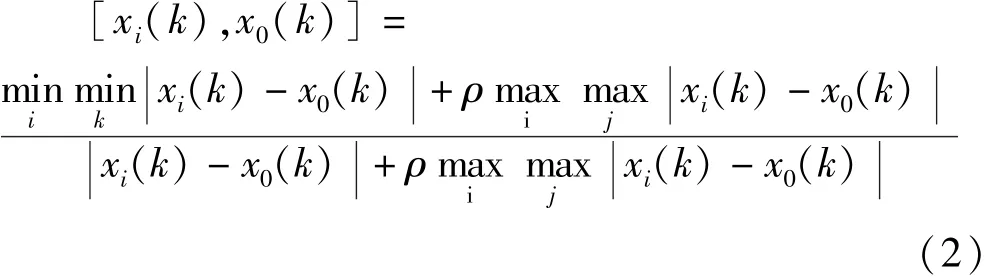
式中:ρ为分辨系数,允许在0与1之间适当调整,在最少信息原理下,分辨系数0.5。目标矢量Xi对于基准序列X0的关联度为:

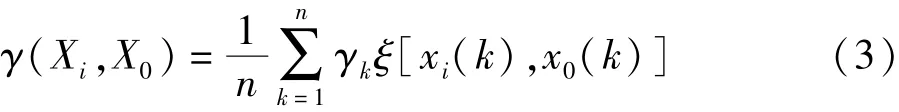
使用Matlab软件用以上公式对矫正法数据进行关联系数计算,得到结果见表4。

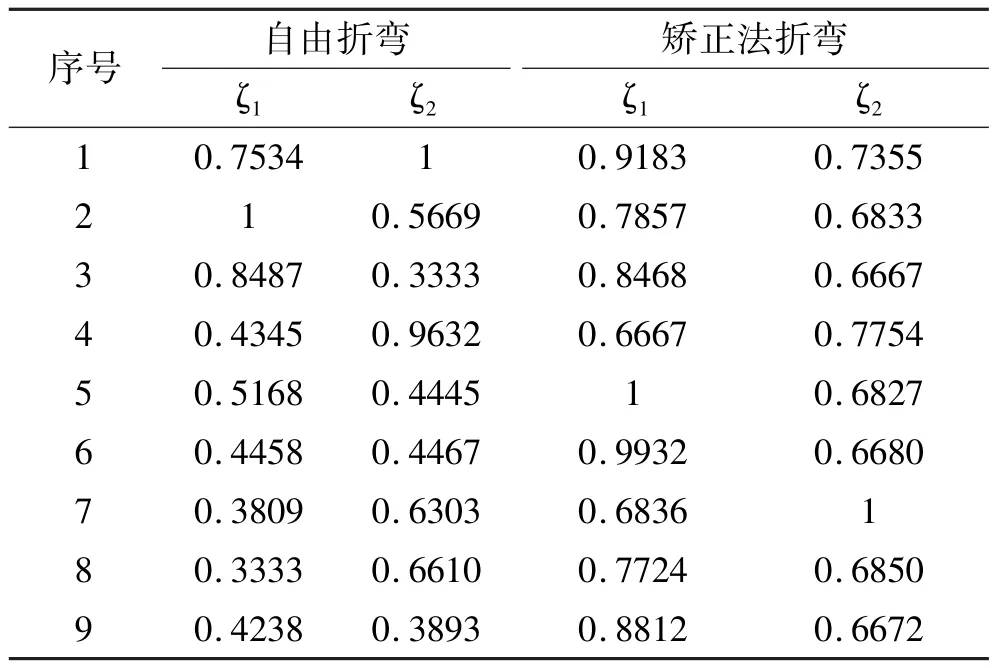
表4 目标函数的灰色关联系数Tab le 4 The ob jective functions of the grey correlation coefficient

中厚板折弯成形中,既要减小成形件弯曲回弹角,又要减小折弯最大成形力。综合考虑各方面的影响,两个目标函数的设计权重相等,即λ1=λ2=0.5。根据式(2),计算得到目标函数的灰色关联度见表5。

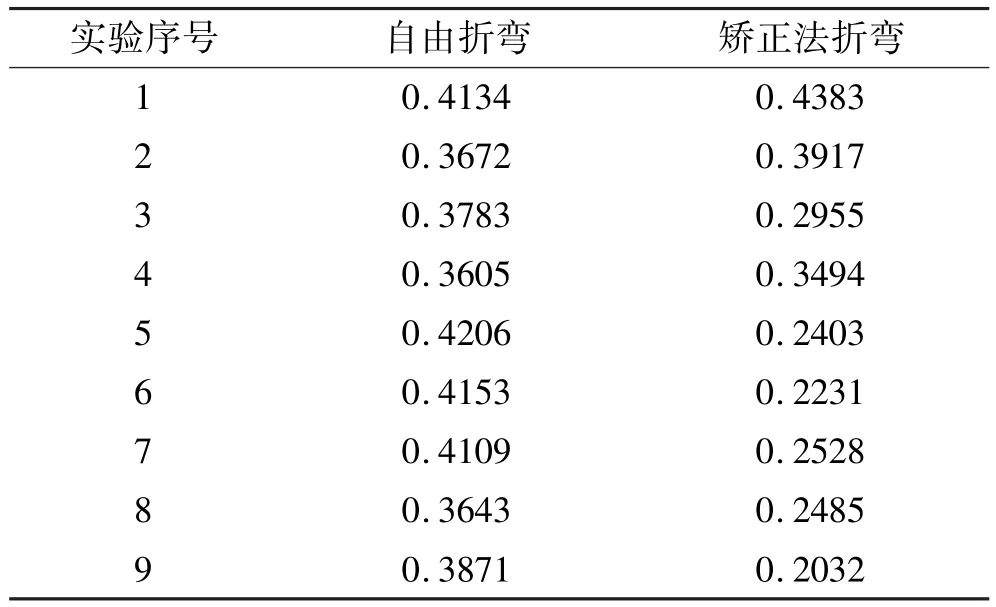
表5 目标函数的灰色关联度Tab le 5 Grey relational grade of ob jective functions

3 对比实验结果分析

经过灰色相关性分析得出自由折弯的第一组和矫正法折弯的第5组工艺参数对目标函数的响应值最大。将矫正法折弯模拟的最优解与自由折弯模拟的最优解进行对比,自由折弯的回弹角为1.471 23,矫正法折弯的回弹角为-0.0068,可见,矫正法折弯件的回弹角远远小于自由折弯模具折弯件的回弹角。

4 折弯实验

4.1 模具设计

利用优化后的参数对模具进行设计,选取凸模圆角16 mm,矫正量3.5%,摩擦因数0.1,坯料选用200 mm×80 mm×16 mm厚Q345钢,并在压力机进行实验。图7为折弯模具。

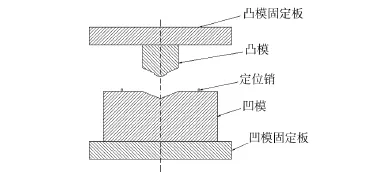
图7 折弯模具示意图Fig.7 Bendingmould diagram

4.2 实验结果分析

图8为材料的成形件,经测量,角度为135°(万能量角器测量精度到分,不能检测出秒的数值,所以结果并非严格135°,但结果已经相对理想),测量如图8所示。

图8 成形件Fig.8 Formed part

由图中可知折弯件符合标准要求。说明选取的的成形参数合理,且使用灰色关联度优化,多自变量、多目标中厚板弯曲成形工艺参数具有正确性与可行性。

5 结论

1)通过对比实验明显显示基于灰色系统理论的矫正法回弹控制效果远远优于自由折弯模具的回弹控制效果。

2)对于矫正法,存在负回弹的现象,且当凸模圆角小于板料厚度时,负回弹现象尤为明显。

3)根据模拟及实验结果可知,矫正法工艺参数将对高强钢厚板折弯进行回弹具有优秀的控制,能够保证成形件的成形精度,所以矫正法工艺在高强钢中厚板折弯成形设计中具有实际应用前景。

[1]肖景容,姜奎华.冲压工艺学[M].北京:机械工艺出版, 2006. XIAO Jing-rong,JIANG Kui-hua.Stamping Technology [M].Beijing:China Machine Press,2006.

[2]BALUN T,TANG SC,CHAPPUIS L B.Application of Mechanical Methods to Evaluation of Forming and Process Design[C]//SAE Trans of Materials&Manufacturing,1993, 930521:727—733.

[3]JAMLIMR,ARIFFIN A K,WAHAB D A.Integration of Feedforward Neural Network and Finite Element in the Draw-Bend Springback Prediction[J].Expert Systems with Applications,2013,41(8):3662—3670.

[4]程军政.大型高精度赋形雷达天线制造技术研究[D].南京:南京理工大学,2013. CHENG Jun-zheng.Technology Research of Large Highprecision Vehicle Radar Antenna Manufacturing[D].Nanjing:Nanjing University of Science&Technology,2013.

[5]张亦良,崔栓伟,李晓延.液压支架主要承载构件焊接残余应力对比分析[J].焊接学报,2013,34(7):89—93. ZHANG Yi-liang,CUI Quan-wei,LI Xiao-yan.The Main Load-carrying Member of Hydraulic Support Comparative A-nalysis ofWelding Residual Stress[J].Journal ofWelding, 2013,34(7):89—93.

[6]杨晓东,需艳春,尚建丽,等.建筑钢结构熔透对接焊缝缺陷对焊缝抗拉承载力影响的研究[J].西安建筑科技大学学报,2011,43(5):730-734. YANG Xiao-dong,XU Yan-chun,SHANG Jian-li,et al. Study on the Influence of Penetrated ButtWeld Defects on Wed Tensile Earring Capacity[J].Journal of Xi'an University of Architecture&Technology,2011,43(5):730—730.

[7]KOJIA,YOSHIKIK,YUJIM.Cyclic Testing of Beam-tocolumn Connections with Weld Defects and Assessment of Safety of Numerically Modeled Connections from Brittle Fracture[J].Engineering Structures,2000,22(12):1596—1608.

[8]SAIDIA R,ATASHIPOUR SR,KESHAVARZIH.Bending Analysis of Thick Laminated Rectangular Plates Using aBoundary Layer Function[J].Proceedings of the Institutions of Mechanical Engineers,2010,224(C10):2073—2081.

[9]孙彩华.高强度钢板折弯工艺探讨[J].煤矿机械,2002 (11):52—53. SUN Cai-hua.Approaching Bending Technology about High Strength Steel Plate[J].Coal Mine Machinery,2002(11): 52—53.

[10]ANA M,UIRAO COCLHO,FRANCSK BIJLAARD.Experimental Behavior of High Strength Steel End-plate Connections[J].Journal of Constructional Steel Research,2007,63 (9):1228—1230.

[11]Universität Stuttgart.Wolter,KH:Freies Biegen von Blechen.VDI-Forschungsh.435,Düsseldorf:VDI,1952.

[12]周昌玉,贺小华.有限元分析的基本方法及工程应用[M].北京:化学工业出版社,2006. ZHOU Chang-yu,He Xiao-hua.The Basic Method of Finite Element Analysis and Engineering Applications[M].Beijing:Chemical Industry Press,2006.

[13]陈立周.稳健设计[M].北京:机械工业出版社,1999. CHEN Li-zhou.Robust Design[M].Beijing:China Machine Press,1999.

[14]WANG SW,SUN S J,WEN A L,et al.Research of Fatigue Limit and Stress Concentration on Structural Steel with Double-notches[J].Key Engineering Materials,2010,419/ 420:849—852.

[15]孔炎,薛克敏,李萍,等.基于正交试验和灰色系统理论的高强钢厚板折弯优化成形模拟及实验[J].塑性工程学报,2014,(5),11-14. KONG Yan,XUE Ke-min,LIPing,et al.Optimized Simulation and Experiment on High-strength Thick Steel Plate Bending Based on Orthogonal Test and Grey System Theory [J].Journal of Plasticity Engineering,2014(5):11—14.

[16]邓聚龙.灰色系统理论[M].武汉:华中科技大学出版社,2002. DENG Ju-long.The Grey System Theory[M].Wuhan:Huazhong University of Science&Technology Press,2002.

[17]王新华,陈登.简明冲模设计手册[K].北京:机械工业出版社,2008. WANG Xin-hua,CHEN Deng.Concise Die Design Handbook[K].Beijing:China Machine Presss,2008.

Optim ization on 135°Orthosis Bending and Springback of Q345 Steel Plate Based on Contrast Test

LIU Jia-hao,DU Yong,XUE Ke-min,ZHANG Heng-guang,TIAN Yao-jiang,YAO Jia-wei,GE Zi-liang
(School of Materials Science&Engineering,Hefei University of Technology,Hefei230009,China)

This paper explored more effective bendingmethod targeting at the problem of complex process and unstable results by the compensating method for calculation of the free springback.This paper adopted the comparison test using Pearson related coefficients and the gray system theory.The test took the Q345 steel of 16 mm thickness as the research subject to obtain the correlation coefficientof the processing parameters to the springback angle,taking punch radius,friction coefficient and rectification as the variables and springback angle and maximum forming force as the objective functions.The FEMsimulation was used to verify the optimized parameter combination.The springback control effect by the orthosismethod wasmuch better than that by the free bendingmold.The FEMverification showed the design and the die trialwith the optimized processing parameters can improve the forming quality and had significant guidance for practical production.

thick plate bending;contrast test;orthosismethod;springback angle

10.3969/j.issn.1674-6457.2015.04.007

TG386

:A

:1674-6457(2015)04-0031-06

2015-04-22

刘佳灏(1994—),男,天津人,本科生,主攻精密塑性成形。

薛克敏(1963—),男,安徽人,教授,博士生导师,主要研究方向为精密塑性成形理论及工艺、成形过程数值模拟、专家系统以及人工神经网络。