局部阴影条件下光伏阵列最大功率点跟踪方法对比研究

梁晓莉，戚 军，张有兵，谢路耀

(浙江工业大学信息工程学院，浙江 杭州310023)

1 引言

当今世界面临着能源危机和环境污染两大问题，太阳能资源丰富，对地域没有限制，逐渐成为各国开发和应用新能源的主要选择。最大功率点跟踪(Maximum Power Point Tracking，MPPT)技术的应用大大提高了太阳能光伏系统的发电效率［1］。

传统的MPPT方法例如开路电压法、短路电流法、爬山法、电导增量法等［2-5］，根据直接测量到的实时电压和电流，进行简单的计算分析，跟踪最大功率点(Maximum Power Point，MPP)。但是传统MPPT方法易困于局部MPP［6］，在局部阴影条件下跟踪精度往往过低。而基于智能优化的MPPT方法［7］虽然适用于各类阴影情况，但是在跟踪过程中存在精度不确定性问题，并且往往有特殊的要求，如人工神经网络法［8］需要大量的训练样本，模糊逻辑控制法［9］依赖于设计者的经验和直觉。故目前光伏阵列MPPT方法主要采用代数MPPT方法。

近年来，大量文献研究了基于代数算法的适用于局部阴影条件的MPPT方法，其准确性、跟踪过程的动态性能与局部阴影状况有着密切联系。如何从中选择适用于实际阴影条件的MPPT方法，目前文献中尚无明确结论。因此，本文通过对大量局部阴影案例的仿真分析与统计对比，对这些方法的实现原理、跟踪性能等方面进行总结归纳。希望能为MPPT技术的进一步发展及实际工程中MPPT方法的选取提供一些借鉴。

本文介绍了几类多峰MPPT方法的工作原理，针对局部阴影的形状进行仿真案例设计，列举各类多峰MPPT方法在跟踪准确度、动态功率振荡方面的仿真结果并对其进行分析说明，并在此基础上总结了多峰MPPT算法的静态跟踪性能、动态跟踪性能以及MPPT效率。

2 多峰MPPT方法的实现原理

为了寻找到多峰功率-电压(P-U)特性曲线上的全局最大功率点，不少研究工作者进行了不懈的探索，提出了一些基于代数算法的多峰MPPT方法。下文介绍几种新兴的多峰MPPT方法。

2.1 负载线交点法

负载线交点法(Load Line Intersection，LLI)［10］的主要思路是:如果出现了局部阴影，首先找到负载线和电流-电压(I-U)曲线的交点作为新的工作点，负载线的斜率Rpm由式(1)定义，然后用传统MPPT方法(如爬山法、电导增量法等)来追踪全局MPP。

式中，Uoc为开路电压;Isc为短路电流。

2.2 负载线对称法

负载线对称法(LoadLineSymmetry，LLS)［11］的原理是在局部阴影条件下首先以负载线Rpm(即式(1))为对称轴，将工作点设置在全局MPP附近，然后再用传统MPPT方法跟踪全局MPP。

图1为MPPT方法原理图。如图1(b)所示，局部阴影产生后，工作点从A1突变至A2，根据对称原理可以找到新的工作点A3，然后用传统MPPT方法跟踪到A3所在山峰的峰值。

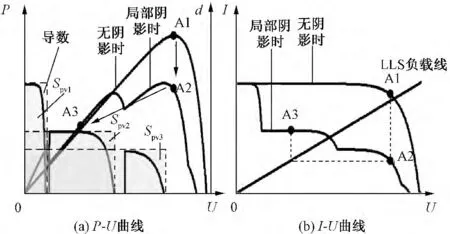
图1 MPPT方法原理图Fig．1 SchematicdiagramofMPPTmethods

2.3 P-U曲线斜率法

P-U曲线斜率法(PowerCurveSlope，PCP)［12］主要根据工作点∂P/∂U的符号变化来跟踪全局MPP。当局部阴影发生时，用爬山法跟踪到一个局部MPP(记为点A)，然后首先在点A的左侧检测∂P/∂U，若∂P/∂U为正，就要在左侧继续搜索，直至∂P/∂U为负，表明点A的附近存在另一个MPP(记为点B)。若点B的功率大于点A，记录点B的功率和电压，继续向左搜索。若点B的功率小于点A或电压达到最小电压阈值，就转换到点A右侧重复上述步骤继续搜索。

2.4 斐波那契数列搜索法(FibonacciSearch，FS)

斐波那契数列搜索法［13］采用了转换和约束策略。每次迭代中，要在P-U曲线上取4个测量点，从0到Uoc的方向依次为和，搜索时先比较和的功率，判断下一步工作点将移向左边或右边，如式(2)所示:

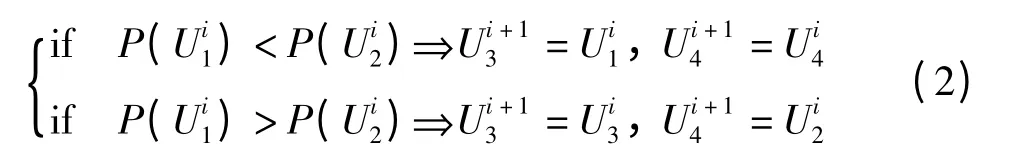
2.5 导数定位法

导数定位法(DifferentialCoefficientLocation，DCL)［14］是在归纳局部阴影条件下光伏阵列导数-电压曲线输出特性的基础上提出的。图1(a)展示了DCL方法跟踪全局MPP的基本过程:局部阴影条件下，首先比较各个导数等效面积Spvi即式(3)，Spvi值最大的区间是全局MPP所在的区间。然后就可以采用传统MPPT方法在所得到区间内跟踪最大功率点。

式中，di为P-U曲线上每个区间上升段斜率最大点的斜率;Ui为相应区间内斜率由正到负变化的临界点电压。

DCL方法斜率的计算取决于搜索时的采样间隔，其搜索间隔越大，算法跟踪准确度越低，但动态功率振荡越小。

不同运行条件下，上述MPPT算法的静态跟踪特性(能否跟踪到全局MPP)、动态跟踪特性(跟踪速度、功率振荡等)等存在较大差异，下文将通过对大量局部阴影案例的仿真来进行对比分析。

3 仿真阴影案例

对于如图2所示n×m的光伏阵列，将光伏阵列分成m串，考虑到相同的阴影在同一串组件上的不同位置遮挡、同一串组件在光伏阵列的不同位置与其他串组件并联不影响光伏阵列的输出特性［15］，假设每一串上的阴影长度从左往右依次递减。将光伏阵列中阴影长度相同的组件串分为一组，一般分组数x越多，光伏阵列P-U曲线上的山峰越多。根据分组数不同，n×m的光伏阵列可分为min{m，n}类阴影。

假设阴影区域辐照度均匀分布，同时温度统一设为25℃，将阴影强度分为10个等级，无阴影处的光照强度为1000W/m2，阴影处的辐照度按100W/m2依次递减，直至100W/m2。若阴影强度分为y个等级，则对应分组数为x的阴影案例数Nx为:

图2 阴影案例的设置Fig．2 Cases setting for shade

本次仿真采用7×7的光伏阵列，当阴影相同的组件串的分组数由1到7变化时，可产生7类阴影，具体案例设置详见表1，表中针对每种阴影类型均设置了10种阴影辐照度，分别为100W/m2、200W/m2、300W/m2、400W/m2、500W/m2、600W/m2、700W/m2、800W/m2、900W/m2、1000W/m2。

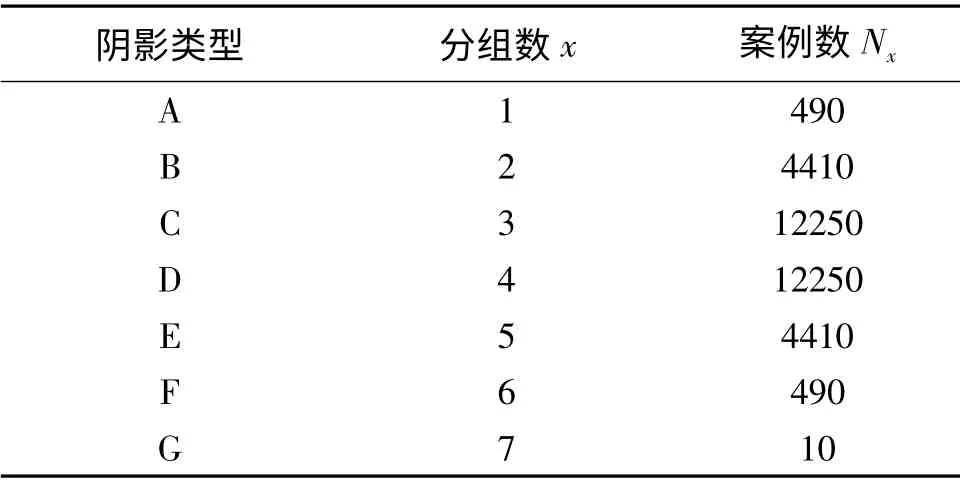
表1 7×7光伏阵列局部阴影案例设置Tab．1 Partial shade cases setting for 7×7 photovoltaic array

4 MPPT方法对比仿真分析

仿真所采用的光伏组件模型均为工程模型，光伏组件参数为Uoc=22V，Isc=8.58A，Umpp=17.7V，Impp=7.94A，填充因子FF=0.94。定义任意一个案例i的MPPT跟踪误差Ei为:

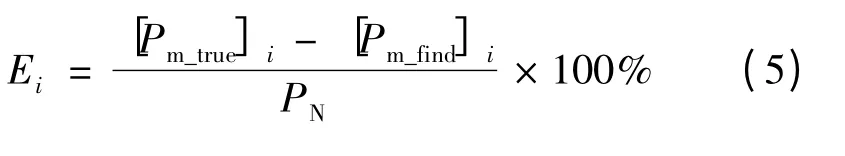
式中，［Pm_true］i为案例i中光伏阵列的真实MPP功率;［Pm_find］i为案例i中算法搜索到的MPP功率;PN为标准测试条件(Standard Test Condition，STC)，即辐照度为1000W/m2、温度为25℃时的额定功率。

仿真中将搜索误差E分为三档:小于0.1%、0.1%～10%和大于10%。误差小于0.1%时，可以认为算法成功跟踪到全局MPP;误差处于0.1%～10%时，虽然算法并未跟踪到全局MPP，但功率损失尚可接受。误差大于10%时，光伏阵列的功率损失较多，若此种情况频繁出现，必须对MPPT算法进行改进。

4.1 最大误差

图3为各种多峰MPPT方法在每类阴影下的最大误差对比图。由此可见:对于大多数MPPT方法而言，矩形阴影块数(即分组数x)较少时(2～4块)，各类算法的最大误差都较大，例如LLS在阴影B下最大误差达到了45.92%，PCP在阴影B下的最大误差有25.65%之多;而对于FS，随着矩形阴影块数的增加，最大误差几乎呈直线下降。就这五种MPPT方法而言，矩形阴影块数较多时，最大误差反而并不高。这是因为当矩形阴影块数较多时，光伏阵列的P-U曲线山峰数量多，降低了各个山峰峰值间的差距。

图3 多峰MPPT方法在各类阴影下的最大误差对比Fig．3 Maximum error comparison formulti-peak MPPT methods under different shade conditions

4.2 均权误差

由于阴影无法事先预测，均权误差可以帮助了解MPPT算法跟踪时的整体功率损失。计算均权误差E∑的公式为:

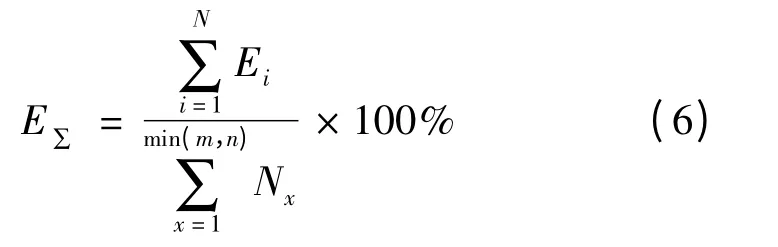
式中，N为所有阴影情况的总案例数，即式(6)中的分母。

均权误差的仿真结果如图4所示，可以看出，上述MPPT方法在34310个典型局部阴影情况下的均权误差处于较低水平(低于4%)。相对而言，PCP及FS的均权误差较小，PCP的均权误差甚至只有0.06%，LLS的均权误差最大，接近3.5%。

图4 多峰MPPT方法均权误差对比图Fig．4 Mean square error comparison formulti-peak MPPTmethods

4.3 算法成功率

如图5所示，多峰MPPT方法成功跟踪到全局MPP案例所占比例均随着矩形阴影块数的增多而降低，即矩形阴影形状越复杂，P-U曲线山峰个数越多，MPPT算法越不容易成功跟踪到全局MPP。

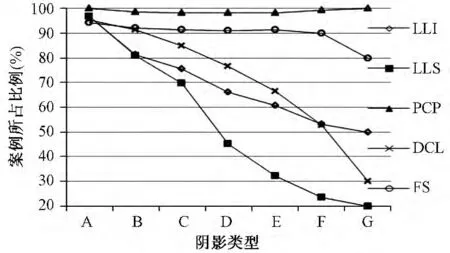
图5 误差小于0.1%案例所占比例对比图Fig．5 Proportion comparison of cases error＜0.1%

如图6所示，各类算法(LLS除外)完全失效案例所占比例在不同的矩形阴影类型下基本保持不变，即大部分的多峰MPPT算法完全失效与否与阶梯状阴影复杂度无较大关系。即使在阴影形状较简单、P-U曲线山峰个数较少的情况下也有较大可能会完全失效。而LLS法完全失效案例所占比例随矩形阴影块数的增加而增加，该方法完全失效的比例较大，在这方面可能需要进一步的改进。

图7对比了多峰MPPT算法在所有案例下的动态跟踪误差。这些方法成功跟踪到全局MPP的案

图6 误差大于10%案例所占比例对比图Fig．6 Proportion comparison of cases error＞10%

例所占比例均超过了50%，并且即使并未跟踪到MPP，造成较大损失的概率也较小。

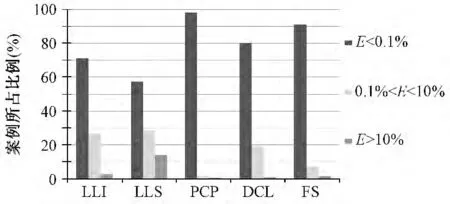
图7 多峰MPPT算法跟踪误差汇总图Fig．7 Error summarizing ofmulti-peak MPPTmethods

4.4 动态性能

MPPT方法跟踪过程中的功率振荡可分为静态功率振荡和动态功率振荡两种。静态功率振荡主要指达到稳态后的功率波动，与仿真中的参数设置相关，同一种算法在不同的参数设置下也会有不同的静态功率振荡表现;而动态功率振荡主要指算法跟踪过程中，工作点变化造成的功率波动。下文将讨论多峰MPPT方法跟踪过程中的动态功率振荡，但不考虑局部阴影发生瞬间的功率振荡。MPPT跟踪过程的起始点选取方法如下:LLI选择负载线和I-U曲线的交点，LLS选择经由负载线对称后找到的新工作点(即A3)，PCP选择跟踪到的第一个MPP。

仿真中的功率振荡计算方法如下:

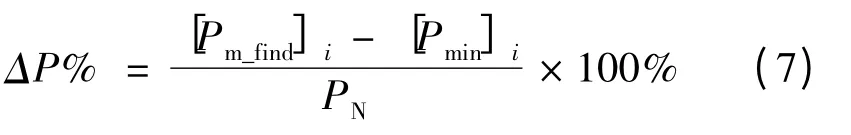
式中，［Pmin］i表示案例i下MPPT算法跟踪过程中工作点达到的最小功率。

多峰MPPT算法在跟踪过程中的动态功率振荡仿真结果如图8所示。LLI和LLS两种算法功率振荡小于10%的比例较高，而几乎不存在功率振荡大于50%的案例，在实际使用时，可以避免对外部电网以及用电设备造成较大冲击。而PCP、DCL以及FS三种算法的动态功率振荡主要分布在30%～90%，功率振荡较大，若光伏电站容量较大，可能对外部电网造成较大冲击，此时需要增加一定的功率平滑措施或设备。

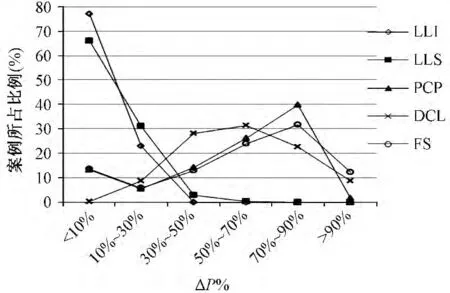
图8 多峰MPPT算法功率振荡对比图Fig．8 Power oscillation comparison formulti-peak MPPTmethods

4.5 MPPT效率

根据欧洲电工标准化委员会的标准BS EN 50530-2010，MPPT效率可以定义为测试时间TM内，逆变器从光伏组件获得的直流电能PDC与理论上光伏组件在MPP输出的电能PMPP的比值:

仿真中假设每个案例持续时间一致，式(8)可以简化为:

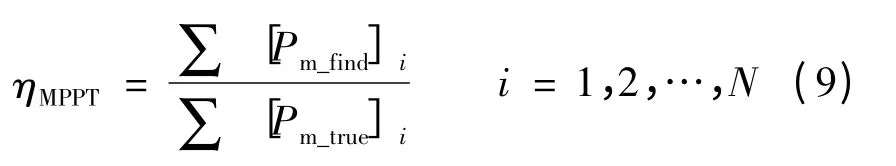
由此可得到多峰MPPT算法在各类阴影下的MPPT效率，如图9所示。LLI、PCP及FS的MPPT效率几乎不受阴影块数的影响，并且保持在较高的水平，而LLS和DCL的MPPT效率随阴影块数的增加而有明显下降。整体而言，这五种MPPT算法的MPPT效率表现都不错。

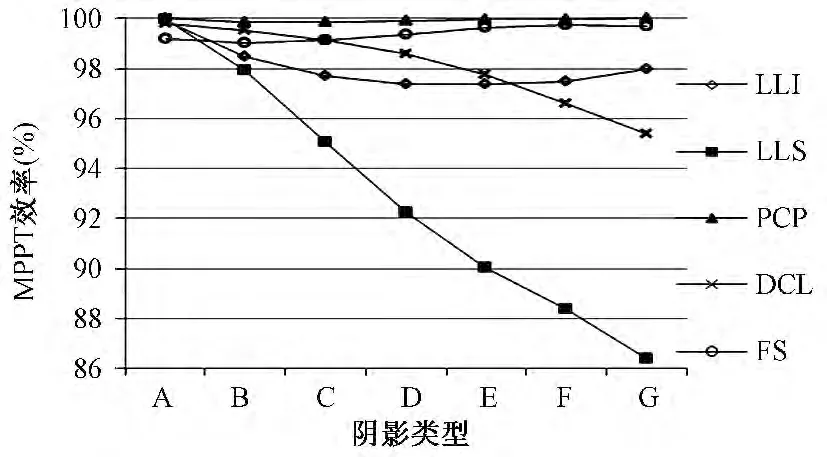
图9 多峰MPPT算法MPPT效率对比图Fig．9 MPPT efficiency comparison for multi-peak MPPTmethods

5 MPPT算法性能对比

MPPT算法的性能具体包括跟踪速度、复杂度、经济成本和跟踪效率等，其中跟踪速度与算法参数设置密切相关，跟踪效率与光伏阵列遭遇的具体阴影变化状态相关。本文对多峰MPPT算法的静态跟踪性能(最大误差、MPPT成功率)、动态跟踪性能(功率振荡)、MPPT效率等性能进行了综合对比分析，结果如表2所示，可以发现:

(1)静态跟踪性能:5种多峰MPPT算法的静态跟踪性能表现各异，PCP的算法成功率最高，FS紧随其后，但这两种方法的最大误差较大;DCL和LLI的最大误差较小，但成功率一般;而LLS的算法成功率较低，并且受阴影复杂度影响较大。

(2)动态跟踪性能:5种多峰MPPT算法中LLI和LLS功率振荡较小，而PCP、DCL以及FS功率振荡较大。

(3)MPPT效率:5种多峰MPPT算法的MPPT效率表现都不错，LLI、PCP及FS的MPPT效率保持在较高的水平，而LLS和DCL的MPPT效率略微偏低。

表2 多峰MPPT方法的性能比较Tab．2 Performance comparison formulti-peak MPPTmethods

考虑到不同参数对系统仿真结果的影响，对不同类型光伏组件(薄膜、单晶硅、多晶硅等)构成的系统进行了对比仿真分析，发现光伏组件Uoc、Isc和填充因子等参数对上述结论并无太大影响。由于篇幅所限，不再赘述。

6 结论

针对如何评价多峰MPPT方法在复杂阴影下的跟踪性能的问题，本文首先介绍了这些方法的基本原理，然后应用Matlab平台对其跟踪准确性、动态功率振荡等进行仿真分析，同时在静态性能、动态性能和MPPT效率等方面进行了对比分析，最后得到的结论包括:

(1)PCP和FS静态性能和MPPT效率表现较好，而动态性能则较差;

(2)LLI和LLS动态性能较好，但静态性能以及MPPT效率较不理想;

(3)DCL各方面均处于中等水平。

［1］周林，武剑，栗秋华，等(Zhou Lin，Wu Jian，Li Qiuhua，et al．)．光伏阵列最大功率点跟踪控制方法综述(Survey of maximum power point tracking techniques for photovoltaic array)［J］．高电压技术(High Voltage Engineering)，2008，34(6):1145-1154．

［2］林期远，杨启岳，徐滢，等(Lin Qiyuan，Yang Qiyue，Xu Ying，et al．)．分布式光伏发电系统最大功率点跟踪技术比较研究(Comparison ofmaximum power point tracking techniques for the distributed photovoltaic power generation system)［J］．能源工程(Energy Engineering)，2012，(2):1-10．

［3］Noguchi T，Togashi S，Nakamoto R．Short-current pulsebased maximum-power-point tracking method for multiple photovoltaic and converter module system［J］．IEEE Transactions on Industrial Electronics，2002，49(1):217-223．

［4］Femia N，Petrone G，Spagnuolo G，etal．A technique for improving P＆O MPPT performance of double-stage gridconnected photovoltaic systems［J］．IEEE Transactions on Industrial Electronics，2005，20(4):963-973．

［5］Liu F，Duan S，Liu F，et al．A variable step size INC MPPTmethod for PV systems［J］．IEEE Transactions on Industrial Electronics，2008，55(7):2622-2628．

［6］MeiQ，Shan M，Liuand L，et al．A novel variable step size incremental resistance MPPT method for PV systems［J］．IEEE Transactions on Industrial Electronics，2011，58(4):2427-2434．

［7］朱艳伟，石新春，但扬清，等(Zhu Yanwei，Shi Xinchun，Dan Yangqing，et al．)．粒子群优化算法在光伏阵列多峰最大功率点跟踪中的应用(Application of PSO algorithm in global MPPT for PV array)［J］．中国电机工程学报(Proceedings of the CSEE)，2012，32(4):42-48．

［8］胥芳，张任，吴乐彬，等(Xu Fang，Zhang Ren，Wu Lebin，etal．)．自适应BP神经网络在光伏MPPT中的应用(Self-adaption BP neural network for themaximumpower-point tracking in photovoltaic)［J］．太阳能学报(Acta Energiae Solaris Sinica)，2012，33(3):468-472．

［9］Syafaruddin，Karatepe E，Hiyama T．Artificial neural network-polar coordinated fuzzy controller based maximum power point tracking control under partially shaded conditions［J］．IET Renewable Power Generation，2009，3(2):239-253．

［10］Kobayashi K，Takano I，Sawada Y．A study on a two stagemaximum power point tracking control of a photovoltaic system under partially shaded insolation conditions［A］．IEEE Power Engineering Society General Meeting［C］．2003．

［11］Younghyok J，Dooyong J，Chungyuen W，et al．A real maximum power point tracking method for mismatching compensation in PV array under partially shaded conditions［J］．IEEE Transactions on Industrial Electronics，2011，26(4):1001-1009．

［12］Nabil A，Miyatake M．A novel maximum power point tracking for photovoltaic applications under partially shaded insolation conditions［J］．Electric Power Systems Research，2008，78(5):777-784．

［13］Miyatake M，Inada T，Hiratsuka I，et al．Control characteristics of a fibonacci-search-based maximum power point trackerwhen a photovoltaic array is partially shaded［A］．The 4th International Power Electronics and Motion Control Conference［C］．Xi’an，China，2004.816-821．

［14］胡义华，陈昊，徐瑞东，等(Hu Yihua，Chen Hao，Xu Ruidong，et al．)．阴影下最大功率点跟踪控制(Maximum power point tracking under shadowed conditions)［J］．中国电机工程学报(Proceedings of the CSEE)，2012，32(9):14-26．

［15］戚军，张晓峰，张有兵，等(Qi Jun，Zhang Xiaofeng，Zhang Youbing，et al.)．考虑阴影影响的光伏阵列仿真算法研究(Study on simulation algorithm of PV array considering shade effect)［J］．中国电机工程学报(Proceedings of the CSEE)，2012，32(32):131-138．