风力发电机自循环蒸发内冷系统的静态分岔分析

李 旺，王海峰，顾国彪

(中国科学院电工研究所，北京100190)

1 引言

自循环蒸发内冷是一种安全高效的冷却方式，目前已成功应用于包括三峡700MW水轮发电机在内的多型发电机，并取得了非常好的运行效果。自循环蒸发内冷系统具有无泵自循环、冷却效率高、运行安全可靠、基本免维护等特点［1］。大型风力发电机安装高度高(一般为100m左右的塔台)，安装地点较为分散，这就要求发电机体积小、重量轻、运行安全可靠、维护量小。蒸发内冷式发电机恰好能够满足风力发电的特殊要求，利用风力发电机与水平方向有3°～5°夹角的特点，实现冷却系统的自循环［2］。由于两相自然循环系统中两相阻力与浮升力的非线性关系，当回路系统几何拓扑结构、环境和运行工况等发生大范围变化时，有可能出现系统运行不稳定现象，这种现象的发生会引发系统参数的剧烈波动，导致局部过热，甚至烧毁，给系统的安全运行带来极大的威胁。因此，对应用于风力发电机的自循环蒸发内冷系统的稳定性问题进行研究是十分必要的，其对确保系统的安全稳定运行具有重要意义。

目前，有关两相流动稳定性的研究工作主要集中在反应堆热工设计领域。1973年，Boure等将两相流不稳定性分为静态和动态流动不稳定［3］;Lahey对后来发现的不稳定现象作了补充［4］;Ramos在1985年指出了静态分岔现象［5］;王建军试验观测到了低干度条件下的自然循环流量漂移现象［6］;Knaani等对封闭式两相自然循环系统进行分析，得到系统的多静态解［7］;姚伟从非线性动力学角度出发，针对两相自然循环系统中不稳定现象进行试验和理论探索［8］;匡波等对高干度自然循环系统的静态分岔特性进行了研究［9］。闫静对风力发电机自循环蒸发内冷系统中的稳定问题进行了初步的探索，得出了一些有益的结论［2］。

综上所述，目前尚没有针对风力发电机自循环蒸发内冷系统稳定性的非线性分析。本文基于非线性分岔理论及其DERPAR数值计算方法［10］，采用均相模型［11-13］，对风力发电机自循环蒸发内冷系统的静态稳定性进行了深入研究。首次获得了该系统的两相自然循环静态分岔图，并且分析了系统非线性的本质;结合蒸发内冷系统在风力发电机中应用的特殊情况，对系统进行了参数效应的研究，为系统的优化设计和安全运行提供理论参考。

2 风力发电机自循环蒸发内冷系统模型

风力发电机倾斜自循环蒸发内冷系统基本结构如图1所示，系统由受热空心导体、回液管、集气管、冷凝器构成。单根空心导体是蒸发内冷系统的基本散热单元，本文将以之为对象来研究蒸发内冷系统的静态稳定性问题。为便于分析，对系统作以下假定:①冷凝器具有足够的冷却能力，确保其出口为单相液体，并可维持出口温度恒定，屏蔽了二次侧对一次系统的影响;②导体均匀加热，并且不计入过冷沸腾;③两相段采用一维均相模型计算流动压降;④不考虑沿程压力不同分布所引起的物性变化，所有的计算均按系统温度确定介质物性。

文中所涉及变量，长度变量单位为m，密度变量单位为kg/m3，压力变量单位为Pa，焓变量单位为J，其他变量单位在文中单独标注。

图1 风力发电机倾斜自循环蒸发内冷系统结构示意图Fig．1 Structure of natural circulation inner evaporative cooling system in wind turbine

系统稳定状态下，在循环通道的任意截面处系统的平衡质量流量都是相同的，记为m(单位:kg/s)。与强迫循环系统不同，自然循环系统的平衡质量流量不是一个独立的变量，无法直接给出，它是一个先验未知的变量，由系统的动阻力平衡方程给出:

式中，Q为导体的热负荷，单位:W;Fdrive(m，Q)为系统的驱动力;Fresis(m，Q)为系统的阻力。

2.1 系统驱动力

回液管、空心导体单相段内的液相介质与集气管、空心导体两相段的气液两相介质的密度差，在重力的作用下产生了系统的自循环驱动力，其计算式如下［2，11-13］:

式中，θ为空心导体与水平方向的夹角;H为集气管的高度(即冷凝器到介质出口的高度);L为空心导体的长度;Lth为空心导体中两相段的长度;Ll=m(Hsat－Hin)L/Q为单相段的长度，其中Hin为入口温度下介质的实际焓，Hsat为出口温度下介质对应的饱和液相焓，且有L=Lth+Ll;ρin为回液管中介质的密度;¯ρl为空心导体中单相段介质的平均密度;¯ρtp为空心导体中两相段介质的平均密度;¯ρtpr为集气管中两相介质的平均密度;g为重力加速度，单位:m/s2。

2.2 系统阻力

系统的阻力由循环回路中回液管、空心导体单相段流动阻力，空心导体两相段、集气管两相流动阻力以及加速度压降组成，其计算公式如下［2，11-13］:

式中，f、fl、f

tp和ftpr为均相模型下的流动摩擦系数，依次为回液管、空心导体单相段、空心导体两相段和集气管内的流动摩擦系数;ρl、ρg分别为空心导体出口温度下介质的液相和气相密度;D为空心铜导体的水力直径;A=π(D/2)2为空心截面面积;xe为出口含气率(干度)，其计算公式为:式中，Rout为出口处介质的汽化潜热，单位:J/kg。而系统出口空泡率α与干度xe的关系为:

3 静态分岔分析模型

动力系统的形态通常用微分方程来描述，其中状态变量X∈B，B是适当定义的Banach空间;分岔参数(控制变量)A也属于一个合适的空间。对于给定的A，动力系统的渐进形态(t→∞时的轨迹)十分丰富，解X(t)趋向于一个吸引子。动力系统主要有四种类型的吸引子，本文主要研究平衡点吸引子。

动力系统式(6)的平衡解(稳态解)用方程来定义。在一定条件下，系统在任意小的扰动下，平衡解的拓扑结构(平衡解的个数和位置)会发生根本的变化，这种变化被称为分岔。为直观地表示系统状态变量随分岔参数的变化情况，可在(X，Q)空间中解出系统的平衡点随分岔参数变化的图形，称为静态分岔图。

从分岔理论来说，自循环蒸发内冷系统是典型的耗散结构系统，系统靠消耗外界能量来维持。

当系统在热负荷Q=Q0的情况下处于稳定状态时，流动压头与总的流动阻力损失相等，此时冷却介质的流量m0即为系统在该负荷下的平衡流量。而当系统的热负荷Q变化时，蒸发内冷系统将进行自调节，稳定在新的质量流量m1处。因此，选择热负荷Q(即定子线圈发热量)作为控制参数，质量流量m作为状态变量，构造系统的静态分岔分析模型如下:)

式中，F(m，Q)=Pdrive－Presis。根据式(8)采用DERPAR数值计算方法进行平衡解的数值延拓［10］，就能够得到风力发电机自循环蒸发内冷系统中质量流量m随热负荷Q变化的静态分岔图。

4 静态分岔特性及机理分析

根据式(8)系统的平衡解方程，采用延拓数值算法，以m为状态变量、Q为分岔参数计算系统的静态分岔图。系统具体参数为:冷凝器高度H=2m，空心导体长度L=2m，水力直径D=4.43mm，倾斜角θ=5°，入口过冷度为15K。结果如图2所示。

图2 风力发电机自循环蒸发内冷系统静态分岔曲线Fig．2 Static bifurcation diagram of natural circulation inner evaporative cooling system in wind turbine

图2中，C点Q=Q2和D点Q=Q1为分岔点，在这两点蒸发内冷系统发生静态分岔。当热负荷Q有一微小的变化时，解的拓扑结构发生改变。系统动力和阻力随质量流量的变化曲线如图3所示。当Q＜Q1时，系统存在唯一的平衡解，对应于图3(a)动力和阻力曲线的交点;当Q＞Q2时系统也只存在唯一的平衡解，对应于图3(c);在Q1＜Q＜Q2区间，系统存在三个平衡解，如图3(b)所示。也就是说，在给定的热负荷Q下，系统有三种可能的运行状态，而系统到底在哪种状态下运行则取决于它的历史运行状况和外部扰动。图2的系统静态稳定分岔图，为深入研究风力发电机自循环蒸发内冷系统稳定性演化和稳定性物理本质提供了理论基础。

图3 系统动力和阻力随质量流量的变化曲线Fig．3 Force and resistance according tomass flow rate

4.1 平衡点的稳定性分析

运用小扰动原理，可以得到类似于强迫循环系统中Ledinegg准则的稳定性判别准则:

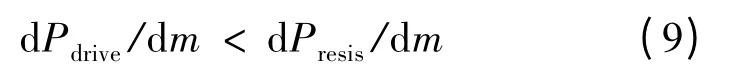
当满足式(9)时，系统的平衡解是稳定的。即当外界扰动使得系统的质量流量m升高(降低)，动力和阻力也将随之降低(升高)。但是，动力降低(升高)的速率大于阻力，故m将降低(升高)重新回到平衡点。因此，系统对m的变化有阻滞作用，从动力系统理论的角度说，此平衡点是稳定的吸引子。反之，若d Pdrive/d m＞d Presis/d m则系统将在外界的干扰下失去平衡，即此时的平衡解是不稳定的吸引子。

据以上分析，在Q＜Q1和Q＞Q2的运行区间内，由图3(a)和图3(b)可知，d Pdrive/d m＜d Presis/d m此区间内系统的平衡解是稳定的;在Q1＜Q＜Q2区间内，由图3(c)可知，左侧和右侧的平衡解满足d Pdrive/d m＜d Presis/d m，为稳定的平衡解，而中间的平衡解满足d Pdrive/d m＞d Presis/d m，为不稳定的平衡解。

4.2 静态分岔的非线性本质

由式(5)可知，α与xe具有强非线性关系，做出α随xe变化的曲线，如图4所示。实际系统运行时，出口处气态介质密度为ρg，ρl/ρg≈142，α-xe非线性关系较强。若增大气态介质密度ρg则α-xe的非线性关系显著变弱。气态介质密度变化时质量流量的静态分岔曲线如图5所示，可以看到，随着气态介质密度的增加，α-xe的非线性关系的减弱，系统质量流量的静态分岔图逐渐变得平坦，当气态介质密度达到一定值后，分岔曲线m-Q就变成单值了。由上述分析可知，风力发电机自循环蒸发内冷系统中的静态分岔现象主要是由气液两相的密度差导致的α-xe的强非线性关系引起的。

图4 气态介质密度变化时α与xe的关系曲线Fig．4 αvs xe diagram according to gas phase density ofmedium

4.3 系统的稳定裕度及极限散热能力

从图2中可以看到，在Q1＜Q＜Q2区间内，沿BC或DE运行时，系统工况稳定，而沿CD段运行则不稳定。在给定的热负荷Q下，系统能够在BC或者DE段运行，而CD段所对应的工作点受到任意小的外部扰动都会向BC或者DE段进行状态漂移。因此，CD段的状态是不可能实际存在的，它只能是系统的一个过渡状态。

图5 气态介质密度变化时质量流量的静态分岔曲线Fig．5 Static mass flow bifurcation according to gas phase density ofmedium

另外一点值得注意的是，当系统在BC或者DE段上运行时，它能够承受小的扰动而维持稳定运行状态，当外界的扰动足够大时，系统的状态将发生跳变。以BC段为例，此时系统对应的平衡状态是高质量流量m和低出口含气率xe，当外部扰动使系统从BC段状态跳变到DE段状态时，此时系统将会维持低质量流量m和高出口含气率xe，反之亦然。这种运行状态的跃变现象称为热虹吸流量突变不稳定性，而BC线和DE线到CD线的距离定义为稳定裕度。

在BC上，随着Q的增大，系统的质量流量增大，散热能力增加，但稳定裕度不断减小。当系统运行到分岔点C时，此时的稳定裕度为零，任意微小的Q的增量都将导致系统质量流量m的跃变，陡降到D点的低质量流量状态。这种质量流量的跃变在蒸发内冷系统中是非常危险的，它将诱发沸腾危机，使发电机线圈温度猛升，甚至烧毁。因此，为了系统的运行安全，定义C点所对应的热负荷Q为蒸发内冷系统的散热极限。

5 静态分岔的参数效应

风力发电机自循环蒸发内冷系统的运行特性随系统运行参数、系统几何拓扑结构的不同而变化。研究风力发电机自循环蒸发内冷系统静态分岔现象的参数效应［14］，是研究风力发电机自循环蒸发内冷系统静态稳定性的一个重要内容。它对风力发电机自循环蒸发内冷系统的优化设计和安全运行有重要意义。

5.1 入口过冷度影响

图6所示为不同入口过冷度下，系统质量流量静态分岔曲线的变化情况。图6中曲线的变化规律表明，当入口过冷度增加时，风力发电机自循环蒸发内冷系统的极限散热能力增加。这是因为在大欠热度条件下，冷却介质可以带走更多的热量。但随着欠热度的增大，BC段的稳定裕度降低，这对于运行在高欠热度、高热负荷条件下的内冷系统是一个不利的因素。另外，在不同的入口过冷度条件下，系统的最大质量流量基本不变。

图6 入口过冷度变化时质量流量的静态分岔曲线Fig．6 Effect of inlet subcooling on bifurcation diagram ofmass flow rate

5.2 冷凝器高度的影响

图7所示为不同冷凝器高度下，系统质量流量静态分岔曲线的变化情况。由该图可以看到，随着H的增大，系统的极限散热能力和最大质量流量都增加。这是因为随着H的增加，系统上升段提供了更大的驱动力使得介质的流速加快，在更高速度的流动状态下，内冷系统能够带走更多的热量。

图7 冷凝器高度H变化时的静态分岔图曲线Fig．7 Effect of H on bifurcation diagram

5.3 空心导体倾斜角影响

风力发电机由于“塔筒效应”与水平方向具有3°～5°的小倾角。图8所示为倾斜角变化时质量流量的静态分岔曲线。由图可知，在3°～5°范围内，随着θ角的增加，系统的极限散热能力和最大质量流量基本不变。因此，在风力发电机自循环蒸发内冷系统设计时可忽略倾斜角θ对系统静态稳定性的影响。

5.4 空心导体水力直径的影响

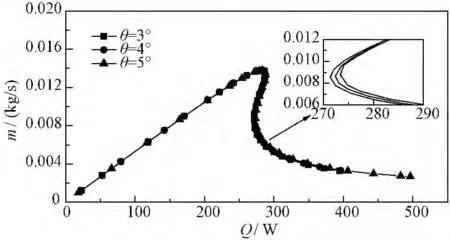
图8 空心导体倾斜角变化时的静态分岔曲线Fig．8 Effect ofθon bifurcation diagram

空心导体水力直径变化时的静态分岔图曲线如图9所示，可以看到，当导体空心矩形截面水力直径D增加时，系统的极限热负荷和最大质量流量显著增加。由式(3)可知，系统的阻力基本与D3成反比，当D增大时，系统的阻力大幅减小，使得质量流量大幅增加，在高速流动状态下系统的极限热负荷和最大质量流量得到了大幅提升。在风力发电机蒸发内冷线圈设计时，可以适当增大D以提高电机散热能力，但D的增大会占用更多的定子槽空间，从而影响电机的其他性能，因此在电机设计时需要综合考虑散热和性能要求。

图9 空心导体水力直径变化时的静态分岔图曲线Fig．9 Effect of D on bifurcation diagram

6 结论

本文基于非线性分岔理论，对风力发电机自循环蒸发内冷系统的静态稳定性进行了研究，给出了系统的静态分岔图解，并讨论了造成系统非线性的主要原因是气液两相的密度差导致的α-xe强非线性关系，给出了系统的稳定裕量和极限散热能力。结合风力发电机的特点，讨论了系统运行参数和几何拓扑结构对系统静态分岔特性的影响，为系统的优化设计和安全运行提供理论参考。

［1］阮琳(Ruan Lin)．大型水轮发电机蒸发内冷系统的基础理论研究及自循环系统的仿真计算(The basic theory research of the inner evaporative cooling system for the large hydro-generator and the simulation of the CLSCsystem)［D］．北京:中国科学院电工研究所(Beijing:Institute of Electrical Engineering，Chinese Academy of Sciences)，2004．

［2］闫静(Yan Jing)．风力发电机蒸发内冷系统中的两相流摩擦压降及不稳定性的基础研究(Study on the two-phase flow frictional pressure drop and instability of the evaporative inner cooling system)［D］．北京:中国科学院电工研究所(Beijing:Institute of Electrical Engineering，Chinese Academy of Sciences)，2013．

［3］Bouer JA，Bergles A E，Tong L S．Review of two phase flow instability［J］．Nuclear Engineering and Design，1973，25(2):165-192．

［4］Lahey T Jr．An assessment of the literature related to LWR instabilitymodes，NUREG-CR［R］．USA:Nuclear Regulatory Commission，1980．

［5］Ramos E，Sen M，Trevino C．A steady-state analysis for variable area one and two-phase thermosy phonops［J］．International Journal of Heat Mass Transfer，1985，28(9):1711-1719．

［6］王建军，杨星团，姜胜耀(Wang Jianjun，Yang Xingtuan，Jiang Shengyao)．低干度自然循环两相流动系统的静态分岔特性(Bifurcation characteristic of two-phase flow in natural circulation system with low steam quality)［J］．原子能科学技术(Atomic Energy Science and Technology)，2007，41(2):180-184．

［7］Knaani A，Zvirin Y．Bifurcation phenomena in two-phase natural circulation［J］．International Journal of Multiphase Flow，1993，19(6):1129-1151．

［8］姚伟(YaoWei)．沸腾两相自然循环系统稳定性的试验与理论研究(Experimentaland theoretical research on the instability mechanism of boiling two-phase natural circulation system)［D］．上海:上海交通大学(Shanghai:Shanghai Jiaotong University)，2000．

［9］匡波，陈宏，徐继鋆，等(Kuang Bo，Chen Hong，Xu Jijun，et al．)．两相流自然循环流量漂移的分岔研究(Bifurcation investigation on flow excursion of two-phase natural circulation)［J］．工程热物理学报(Journal of Engineering Thermophysics)，2005，26(1):88-90．

［10］M库比切克，M马雷克(M Kubicek，M Marek)．分岔理论和耗散结构的计算方法(Computational methods in bifurcation theory and dissipative structures)［M］．北京:科学出版社(Beijing:Science Press)，1995．

［11］鲁钟琪(Lu Zhongqi)．两相流与沸腾传热(Twophase flow and boiling heat transfer)［M］．北京:清华大学出版社(Beijing:Tsinghua University Press)，2002．

［12］徐济鋆，鲁钟琪(Xu Jijun，Lu Zhongqi)．沸腾传热和气液两相流(Boiling heat transfer and gas-liquid twophase flow)［M］．北京:原子能出版社(Beijing:Atomic Energy Press)，2001．

［13］陈听宽(Chen Tingkuan)．两相流与传热研究(Twophase and heat transfer)［M］．西安:西安交通大学出 版 社(Xi’an:Xi’an Jiaotong University Press)，2004．

［14］佟立丽，姚伟，匡波，等(Tong Lili，Yao Wei，Kuang Bo，et al．)．两相自然循环系统的静态分岔特性机理分析(Mechanism analysis on static bifurcation of twophase natural circulation)［J］．核动力工程(Nuclear Power Engineering)，2001，22(3):216-220．