转子动能为外环控制量的永磁同步电动机双闭环矢量控制策略

王安邦 姜卫东 王群京 佘阳阳

1.合肥工业大学电气与自动化工程学院 合肥 230009

2.安徽大学电气工程与自动化学院 合肥 230601）

0 引言

永磁同步电动机因为具备高效率、结构简单和高功率密度等优点，已被广泛用于航空航天、数控机床、机器人和电动汽车[1-3]等诸多领域。由于永磁同步电动机具有多变量、非线性及强耦合的特性，故需要采用较为复杂的控制策略。在永磁同步电动机控制系统中，电动机转速的超调量和调节时间是衡量电动机控制性能的重要指标。目前主要有三种控制方法：变压变频控制、磁场定向的矢量控制[4-6]和直接转矩控制[7-9]，其中矢量控制策略在工业界运用较为广泛。传统的矢量控制策略采用转速、电流双闭环控制，转速的阶跃响应为典型的二次响应曲线，超调量较大且调节时间较长。

文献[10]专门对矢量控制和直接转矩控制进行了比较，直接转矩控制具有更好的动态特性和更简单的调制技术，而磁场定向矢量控制的电动机相电流波形质量更好、转矩脉动更小。随着电力电子技术、微处理器及现代控制理论的发展，许多学者和专家在矢量控制或直接转矩控制的基础上加入了一些算法来提高电动机的响应特性，例如：自适应控制[11,12]、滑模变控制[13,14]和智能控制[15,16]等。

在三相PWM逆变器的控制中，在文献[17]中将电压二次方作为反馈构成控制系统的外环，外环输出的是有功电流给定值，提高了系统的快速性。比较 PWM整流器和永磁同步电动机调速系统，前者是采用电容储存电场能量，后者是采用转子惯量（或者折算后的）储存机械能量，因此这两种算法具有一定的一致性。在整流器的进一步的研究中，文献[18]从 Boost变换器的状态空间平均方程数学模型出发，推导了功率传递关系。在此基础上提出了一种以电流环作为内环、直流侧电容储能环作为外环的反馈控制策略，引入负载功率的前馈，并给出了前馈功率的估计算法，相比较传统的电压、电流双闭环控制策略具有更好的动态特性。

本文提出一种基于转子动能储存的矢量控制策略，以转子动能储能环作为外环，以电流环作为内环，从能量的角度控制电动机。由电动机的动能储能关系可知，电动机的储能与转速二次方成正比关系，转速增加，储能呈二次函数增长。基于转子动能储存的矢量控制策略的外环，使用电动机转子储存动能的给定值与实际值的差值作为输入量，输出量通过解耦得到内环的电流给定值，从而实现对电动机的控制。为了验证基于转子储存动能的矢量控制策略的动态性能，将该策略与传统的矢量控制策略进行比较。最后还研究了负载变化对系统动态性能的影响。

1 永磁同步电动机的能量交换模型

为了简化分析，经坐标变换，将永磁同步电动机模型由ABC轴系变换到dq轴系，如图1所示。

永磁同步电动机在dq轴系下的电压方程为

图1 隐极式永磁同步电动机物理模型Fig.1 Model of non-salient PMSM

式中，Ld为永磁同步电动机的直轴同步电感；Lq为交轴同步电感，隐极式永磁同步电动机Lq=Ld=L；ωr=ωmp0=2 πnp0/60为转子转速对应的电角频率（n为电动机转速，r/min；ωm为电动机机械角频率；p0为电动机极对数）；ψf为永磁同步电动机的转子励磁磁链。为了使电动机转矩电流比最大且不采用弱磁控制，一般控制使id=0，按照基于转子磁链的定向规则ed=0，且eq=ωrψf。（以下分析中所有带上标*的量为给定值或估计值，不带*的量为实际值或反馈值，永磁同步电动机的模型分析中以实际值为依据。）

将式（1）中第一行乘以id加上第二行乘以iq后，得到有功功率的交换关系为

式中，等号左边为驱动器提供的有功功率。等号右边第一项为定子电阻消耗的有功功率；第二项为定子电感内磁场储能增加时所消耗的有功功率，在稳态时磁场储能不变化，该项为零；第三项为电动机磁阻转矩所输出的机械功率，隐极式同步电动机中该项为零；第四项对应于转子磁链转矩所输出的机械功率。

将式（1）中第一行乘以iq减去第二行乘以id后，得到无功功率的交换关系为

式中，等号左边为驱动器提供的无功功率。等号右边第一项为电感内磁场储能总和变化时所消耗的无功功率，在稳态时该项为零；第二项为电感上消耗的无功功率；第三项为电动机为了实现弱磁调速而吸收的无功功率。

综合式（2）和式（3）可知在电动机转矩电流比最大且不采用弱磁控制时，电动机和驱动器之间的能量交换关系为

因为电动机是实现有功交换的工具，所以重点讨论由驱动器所提供的有功功率如何转换为机械功率驱动负载。当忽略掉驱动器的开关器件引起的损耗后，认为永磁同步电动机从驱动器输入的功率减去电阻、电感储能损耗后，全部转换为机械功率输出。机械功率可以写为

机械功率Mp的一部分Ap将使电动机转速增加（也就是使系统所储存的动能增加），另一部分提供负载消耗功率Lp。电动机从驱动器获得的q轴电流分量将全部提供电动机内部消耗和输出的机械功率，电流的d轴分量为无功分量，将其控制设为零。由式（4）和式（5）得

2 以转子储存动能作为外环的永磁同步电动机双闭环矢量控制

基于电动机转子储存的永磁同步电动机控制策略采用的双闭环控制系统中，电动机的转子所储存的动能作为反馈量。因为电动机转子动能储存与电动机转子所需要的加速功率构成微分关系，因此电动机转子动能的实际值与由电动机转速计算的转子动能的期望值的差值经过 PI调节器后输出功率参考值，功率参考值经过与q轴感应电动势计算后得到电流的q轴分量参考值。

电动机转子动能外环的输出的q轴电流分量参考值与实际电流反馈比较后，若无弱磁控制，d轴电流分量参考值为零，两个轴电流与实际电流反馈比较后，经电流环PI调节器产生dq两轴的电压，从而控制永磁同步电动机工作。

2.1 电流内环的设计

永磁同步电动机内环电流控制本质上是控制驱动器输出电压与电动机内反电动势的差值，此差值加在电动机的绕组电阻和电感上，产生电流。

式中,Δud*、Δuq*为加在电动机定子绕组上的用于产生电流的电压。

为了消除dq轴之间的影响，将电流前馈解耦，解耦后式（7）写为

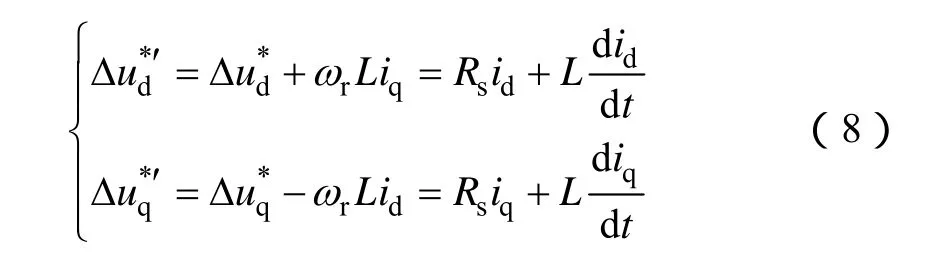
考虑电动机转速可以测量，将式（8）进行拉普拉斯变换，整理后得

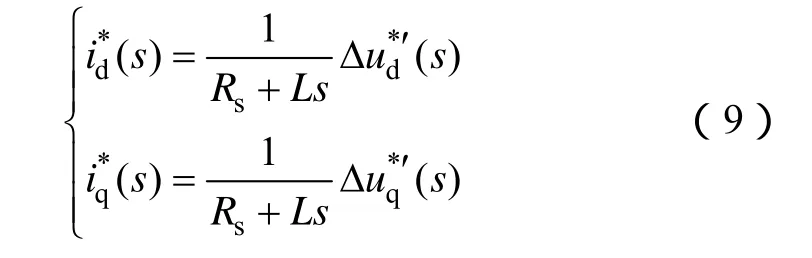
此为一阶惯性环节，PI调节器的反馈控制规律为

式中，kiP、kiI分别为电流内环比例系数和积分系数；id*、iq*分别为外环产生的无功电流和有功电流给定值。由于d轴和q轴结构相似，以q轴的设计为例对内环进行设计。考虑到电流内环应具有较好的快速性，把内环整定为一阶惯性环节，令kiI/kiP=Rs/L，得到

式中，Tc=L/kiI。

最终得到电流内环的控制规律

整个内环的解耦控制策略如图2所示。

2.2 基于转子储存动能反馈的外环设计

图2 电流内环解耦控制框图Fig.2 Diagram of the current loop with decoupling

以转子储存动能为控制目标的策略，选取电动机储存的动能EK作为反馈量，通过PI调节器构成控制系统外环。电动机转子储存动能与电动机转速的二次方成正比，控制转子储存的动能也可以等效于控制电动机转速。通过电动机转速计算出电动机转子实际存储的动能，与由给定转速计算的期望储能值相比后，经储能反馈环PI调节器产生电动机加速功率给定p*A，再加上相应的损耗部分和负载估计值，除以电动机的感应电动势，得到q轴电流给定。由于电动机转子储存动能与电动机的加速功率构成微分关系，即

根据反馈控制规律，通过控制电动机的加速功率就可以控制电动机转子储存动能，设计该环输出为加速功率给定电动机转子储能环的控制规律为

若将电动机定子电阻所消耗的功率和电感储能所消耗的功率及负载消耗的功率进行前馈补偿以后，可以得到电动机需要从驱动器吸收的总功率pD*

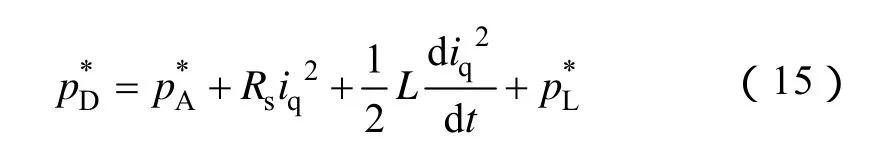
忽略电阻消耗功率和电感储能吸收的功率（该功率远远小于电动机所需的加速功率和负载功率），可以近似认为为了获得较为准确的加速功率控制，需要将电动机负载功率进行估算和前馈。按照上文定向规则，得到电流内环的q轴电流给定值

基于转子储存动能反馈控制策略的框图如图3所示，当将损耗功率和负载功率前馈处理后，可写出闭环传递函数为

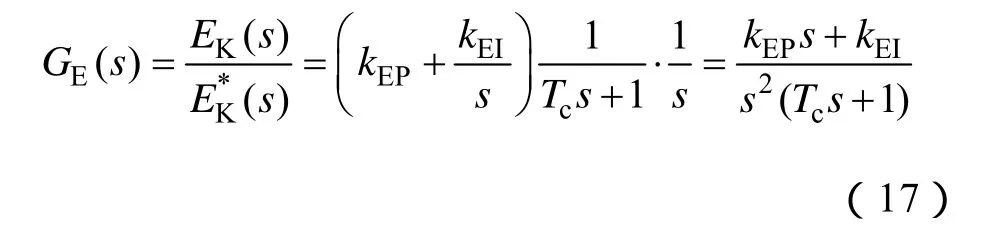
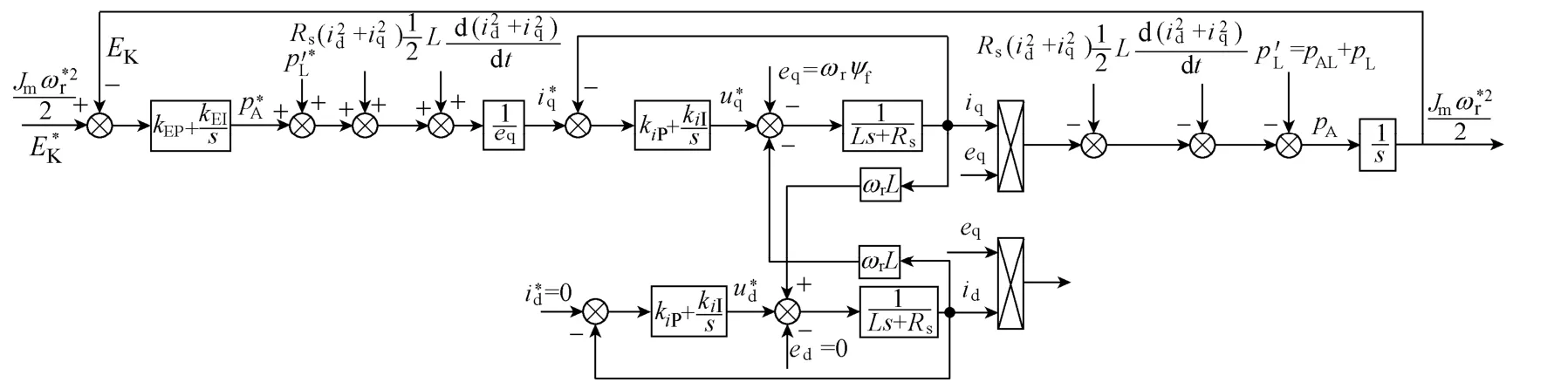
图3 控制系统的整体框图Fig.3 The diagram of the proposed control system

外环按典型Ⅱ型系统设计。给定转子动能储能外环中频带宽hp，由典型Ⅱ型系统控制器参数整定关系得

一般情况下，可取hp=5代入式（18）得

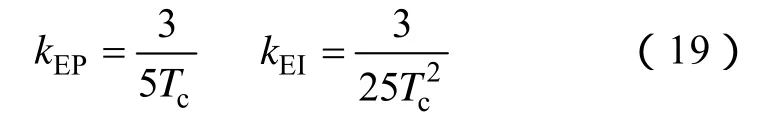
2.3 负载的影响及负载补偿

根据式（13）可知，转子储存的动能与电动机的转动惯量、电动机转速有关。忽略系统的摩擦阻力，考虑到电动机与驱动系统的实际能量交换关系为

式中，Jm、JL分别为电动机轴和负载转动惯量；分别为使电动机轴和负载转速变化时所需要的功率，在负载转速发生变化时，该项不为零，将pAL+pL考虑为一项pL′。

当电动机负载发生变化时，输入功率与负载功率不再平衡，由于PI调节器的滞后性，负载首先与电动机转子动能发生能量交换，引起电动机系统转速的变化。根据功率表达式，忽略电阻消耗功率和电感储能吸收的功率，可以写出负载功率的前馈估计算法。其表达式为

式中，前一项为驱动器输入的功率；后一项为电动机转子储能的变化量。为了消除系统的采样误差，采用多周期平均值来估计负载功率，k为平均的周期数。当将负载功率进行前馈补偿以后，对永磁同步电动机的控制始终可以等效为对其空载控制，消除了负载波动和转动惯量变化对系统性能的影响。基于以上分析，得到永磁同步电动机的基于转子储能反馈和负载功率前馈的控制策略的框图如图3所示。

3 实验结果及其分析

为了验证本文所提出算法可行性，将该控制策略与传统的矢量控制策略进行对比实验，永磁同步电动机控制系统如图4所示。测功机为MAGTROL公司的 HD-815-8，示波器为 Aglient公司的 DSO-X 3014A，电动机转速是由 DSP采集，利用 AD7542数模转换芯片设计的 DA电路输出，电流波形由Tektronix公司的A622电流探头测得。永磁同步电动机的技术参数见下表。

图4 永磁同步电动机控制系统Fig.4 Control system of PMSM

3.1 传统双闭环控制策略和本文所提出控制策略起动时的比较

图5给出了传统双闭环控制策略和本文所提出的控制策略下给定转速分别为 3 0 0 r/m i n、1 0 0 0 r/m i n和2 0 0 0 r/m i n时，电动机的相电流、q轴电流qi和转速起动响应曲线。

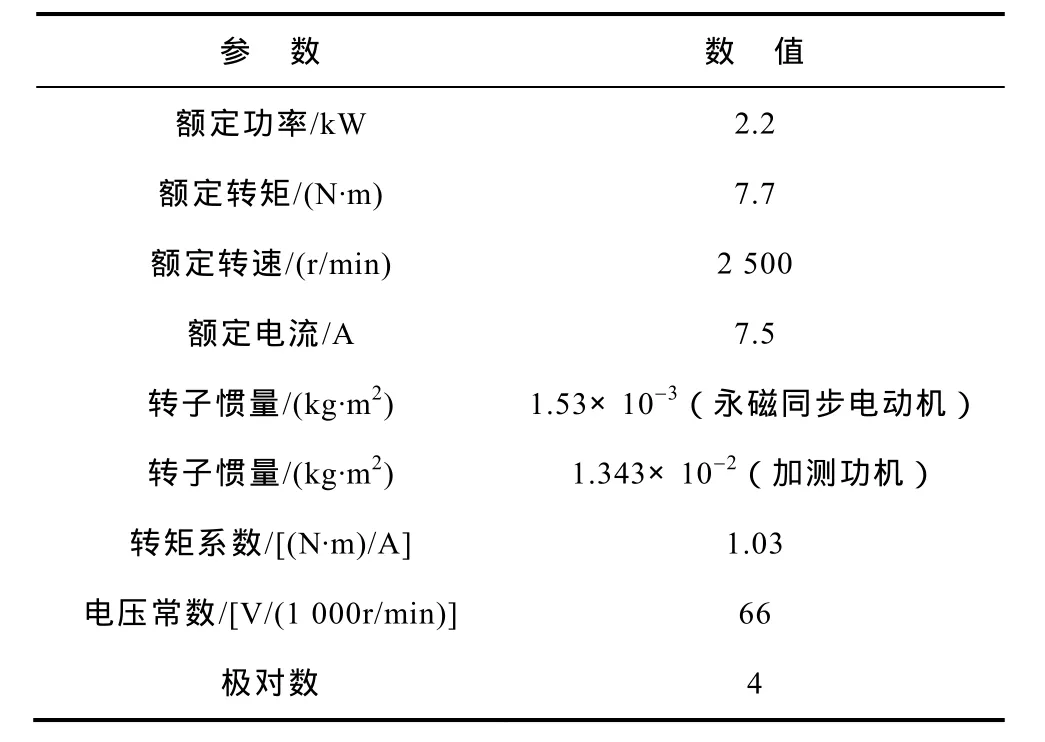
表永磁同步电动机的技术参数Tab.Parameters of PMSM

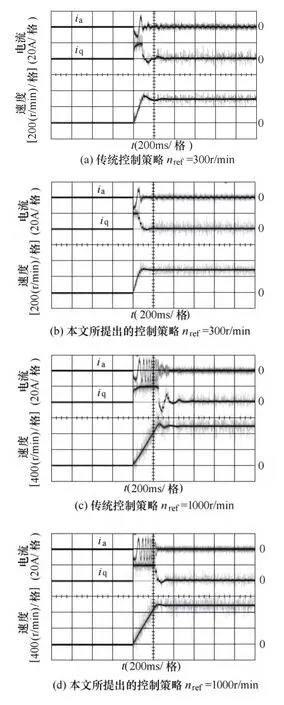
图5 电动机起动实验Fig.5 Experimental results of the startup process

两种控制策略采用不同的外环调节器，相同的电流内环调节器。比较两种算法在电动机起动时的响应特性可以看出：

（1）两种控制策略中，当电动机转速误差较大时，转速外环PI调节器的输出饱和，电动机以最大电流加速，这一过程中，两种控制策略表现出一致的加速性能。

（2）当电动机转速接近设定值时，外环PI调节器中的P调节器开始减小控制比例，而积分调节器开始逐渐增大控制比例，由于本文所提出控制策略在转速误差减小时，P调节器以二次方的关系减小，所以在这一过程中本文所提出的控制策略优于传统的双闭环控制策略。

（3）当电动机转速高于设定值时，外环调节器输出的电流给定会迅速降为零或负值，相比之下本文所提出的控制策略在外环调节器退饱和时优于传统的双闭环控制策略。

事实上，两种控制策略的主要区别在于控制器的外环设计。从q轴电流的曲线看来，本文所提出的控制策略当电动机转速在设定转速附近时，q轴电流能够快速稳定，有效地抑制了电动机的转速振荡。与起动过程类似的结论，也可以在电动机转速给定突减的过程中看出，如图6所示。

3.2 负载转矩突变时对负载估算算法的验证

图6 电动机减速时实验结果Fig.6 Experimental results of the deceleration process

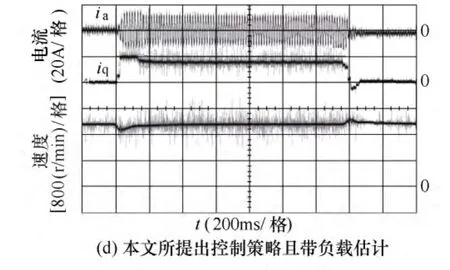
图7 负载转矩突变时的响应特性Fig.7 Experimental results in the step loadtorque conditions

为验证本文所提出算法的动态性能，比较了传统双闭环控制策略和本文所提出控制策略在负载转矩突加、突减时的控制性能，实验结果如图7所示。制效果。可以看出，当突加负载时，转速会发生较大的跌落，由于转速调节器的作用，外环输出的电流给定加大，电动机输出更大的转矩，导致电动机转速上升，从而恢复到给定转速。当带有负载估计算法时，不论是传统控制策略还是本文所提出的控制策略，突加负载时转速跌落和突减负载时转速上升都优于不带负载估计的控制策略，如图7c和图7d所示。这是因为在负载转矩突变时，首先吸收电动机和负载系统中所储存的旋转动能，导致电动机转速下降，根据式（21），可以估计出负载功率的变化。并将前馈叠加到外环电流给定上，从而实现对功率变化的超前控制。从实验结果可以看出，带负载估计的基于转子动能储能反馈控制的系统性能为最优。

3.3 转动惯量变化时负载估计算法的验证

将电动机脱开负载机，比较不同算法下负载惯量变化对电动机起动响应性能。图8给出了负载惯量改变，重新起动电动机时，传统双闭环控制策略和本文所提出的控制策略分别在带和不带负载估计时的响应特性。如图8a和图8b所示，当负载转动惯量改变较大时，未加入负载估计算法，两种控制策略下，都出现了短时振荡，在实际系统中必须修改外环PI参数才能消除振荡。图8c和图8d给出了当负载转动惯量变化较大时，加入负载估计算法，PI参数不做修改情况下的起动波形，两种控制方法均可以达到图5类似的起动性能。由此可见，本文所提出的负载估计算法对于负载惯量的变化具有一定的适应性。

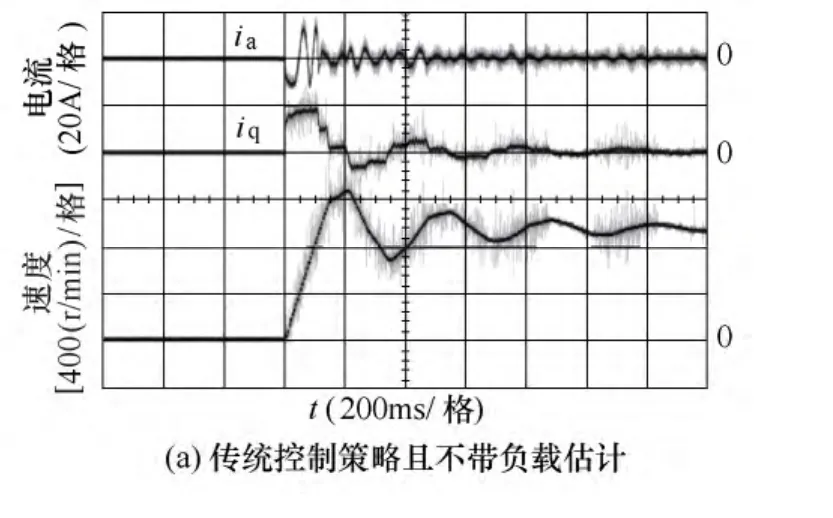
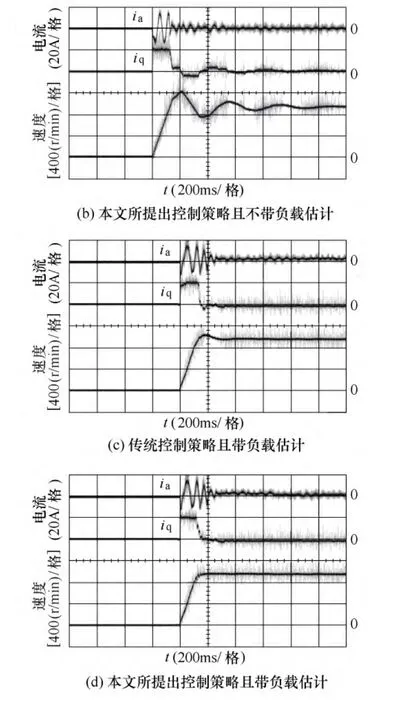
图8 负载转动惯量变化情况下响应特性Fig.8 Experimental results under the load rotational inertia varying

4 结论

本文分析了永磁同步电动机的能量交换模型，提出了以电动机转子储能作为外环反馈的矢量控制策略。由电动机的动能储能关系可知，电动机的储能与转速二次成正比关系，转速增加，储能呈二次函数增长。基于转子动能储存的矢量控制策略的外环，使用电动机转子储存动能的给定值与实际值的差值作为输入量，输出量通过解耦得到内环的电流给定值，从而实现对电动机的控制。即使在相同的转速增量条件下，初始转速较大时，电动机需要更多的加速功率，而这一点在转速、电流双闭环控制下，因为外环调节器采用转速的差值作为输入，是无法实现的；而外环采用动能差值作为调节器输入，则很好地解决了这一问题。经过理论分析和实验验证，本文得到以下结论：

（1）验证了基于能量反馈的矢量控制策略的可行性。

（2）与传统的双闭环矢量控制策略相比，本文所提出的控制策略的动态响应性能更优。

（3）提出了一种负载估计方法，避免了需要根据负载转矩调节控制器参数的问题，并消除了负载转动惯量变化对系统性能的影响。

（4）该控制策略的思想同样适用于其他一些输出量具有明确的能量函数表达式的系统中，例如PWM整流器的直流侧电压控制等。

[1]韩建群,郑萍.一种用于电动汽车的永磁同步电机直接转矩控制的简化方法[J].电工技术学报,2009,24(1): 76-80.

Han Jianqun,Zheng Ping.A simplified direct torque control method of PMSM applied in electric vehicles[J].Transactions of China Electrotechnical Society,2009,24(1): 76-80.

[2]Estima J O,Marques Cardoso A J.Efficiency analysis of drive train topologies applied to electric/hybrid vehicles[J].IEEE Transactions on Vehicular Technology,2012,61(3): 1021-1031.

[3]李耀华,马建,刘晶郁,等.电动汽车用永磁同步电机直接转矩控制电压矢量选择策略[J].电机与控制学报,2012,16(4): 43-49.

Li Yaohua,Ma Jian,Liu Jingyu，et al.Voltage vector selection strategy of the DTC for PMSM used in electrical vehicle[J].Electric Machine and Control,2012,16(4): 43-49.

[4]余佩倡,吴峻,周文武.永磁同步电机矢量控制系统设计[J].电力电子技术,2011,45(11): 105-107.

Yu Peichang,Wu Jun,Zhou Wenwu.The design of vector control system of PMSM based on TMS302F28335[J].Power Electronics,2011,45(11): 105-107.

[5]曹瑜,王旭东.一种改进的永磁同步电机矢量控制系统的研究[J].电力电子技术,2012,46(5): 54-56.

Cao Yu,Wang Xudong.Research on an improved PMSM vector control system[J].Power Electronics,2012,46(5): 54-56.

[6]李耀华,吴俊,郭巧娟,等.永磁同步电机矢量控制的两种实现方法比较[J].微电机,2012,45(1):25-28.

Li Yaohua,Wu Jun,Guo Qiaojuan，et al.Comparison of two ways to implement the FOC for PMSM[J].Micromotor,2012,45(1): 25-28.

[7]Mathapati S,Bocker J.Analytical and offline approach to select optimal hysteresis bands of DTC for PMSM[J].IEEE Transactions on Industrial Electronics,2013,60(3): 885-895.

[8]Xia Changliang,Zhao Jiaxin,Yan Yan,et al.A novel direct torque control of matrix converter-fed pmsm drives using duty cycle control for torque ripple reduction[J].IEEE Transactions on Industrial Electronics,2014,60(6): 2700-2713.

[9]邱鑫,黄文新,杨建飞,等.一种基于转矩角的永磁同步电机直接转矩控制[J].电工技术学报,2013,28(3): 56-62.

Qiu Xin,Huang Wenxin,Yang Jianfei,et al.A direct torque control strategy based on torque angle for permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2013,28(3):56-62.

[10]Aguirre M,Calleja C,Lopez-de-Heredia A,et al.FOC and DTC comparison in PMSM for railway traction application[C].Proceedings of the Power Electronics and Applications 2011: 1-10.

[11]Jin H Z,Lee J M.An RMRAC current regulator for permanent magnet synchronous motor based on statistical model interpretation[J].IEEE Transactions on Industrial Electronics,2009,56(1): 169-177.

[12]黄科元,周滔滔,黄守道,等.永磁伺服系统基于微分自适应补偿的陕速无超调控制策略[J].电工技术学报,2014,29(9): 138-144.

Huang Keyuan,Zhou Taotao,Huang Shoudao,et al.Overshoot and fast response control of PMSM servo system based on differential adaptive compensation[J].Transactions of China Electrotechnical Society,2014,29(9): 138-144.

[13]Corradini M L,Ippoliti G,Longhiss,et al.A quasi-sliding mode approach for robust control and speed estimation of PM synchronous motors[J].IEEE Transactions on Industrial Electronics,2012,59(2):1096-1104.

[14]Zhang Xiaoguang,Sun Lizhi,Zhao Ke,et al.Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation techniques[J].IEEE Transactions on Power Electronics,2013,28(3): 1358-1365.

[15]Lin F J,Hung Y C,Hwang J C,et al.Fault-tolerant control of a six-phase motor drive system using a takagi-sugeno-kang type fuzzy neural network with asymmetric membership function[J].IEEE Transactions on Power Electronics,2013,28(7): 3557-3572.

[16]Han H C,Jung J W.Discrete-time fuzzy speed regulator design for pm synchronous motor[J].IEEE Transactions on Industrial Electronics,2013,60(2):600-607.

[17]王恩德,黄声华.三相电压型 PWM 整流器的新型双闭环控制策略[J].中国电机工程学报,2012,32(15): 24-30.

Wang Ende,Huang Shenghua.A novel double closed loops control of the three-phase voltage-sourced PWM rectifier[J].Proceedings of the CSEE,2012,32(15): 24-30.

[18]姜卫东,吴志清,胡杨.直流电容储能反馈和负载功率前馈的Boost变换器控制策略[J].电力自动化设备,2014,34(8): 103-107.

Jiang Weidong，Wu Zhiqing，Hu Yang.Control strategy based on DC-link capacitor energy feedback and load power feedforward of Boost converter[J].Electric Power Automation Equipment,2014,34(8):103-107.