级联型变流器直流母线空载振荡分析与环路优化设计
2015-06-24陈轶涵龚春英
陈轶涵 陈 杰 韦 徵 龚春英
(南京航空航天大学自动化学院 南京 210016)
0 引言
高压直流电源系统以其高可靠、高效率、结构简单以及易于实现不间断供电的优点成为飞行器电源系统的发展方向[1],随之需要大量采用(DC-DC)-(DC-AC) 结构的航空静止变流器(Aeronautical Static Inverter,ASI)产品。为了保证模块级联后的稳定性,前后级变换器的环路设计优化工作逐步引起国内外专家的重视。
目前两级式变换器稳定性问题的研究主要集中在前后级变换器小信号建模和阻抗匹配角度。文献[2]基于小信号模型,根据内模原理对航空静止变流器的环路中的内模发生器和补偿器的控制参数进行优化设计,据此解决了级联型静止变流器中非线性负载输出电压波形畸变的问题,文献[3,4]通过前级DC-DC变换器前馈控制的方法滤除前级环路中的低频扰动信号,抑制了由后级单相逆变器引起的直流母线两倍低频脉动问题。文献[5-9]在大、小信号建模的基础上,基于Middle Brook教授提出的级联系统阻抗比判据,设计前后级变换器的输入输出阻抗,使前级输出阻抗远小于后级的输入阻抗,指导补偿网络的设计。但是上述研究都是针对变换器中功率或额定功率的电流连续工作状态,未能考虑前后级变换器全负载范围下的小信号模型与两级变换器工作稳定性的关系,尤其是空载或者轻载下直-直变换器工作在电流断续(Discontinuous Conduction Mode,DCM)状态时对级联系统稳定性的影响。
本文基于前级平均电流控制移相全桥直-直变换器在电流连续(Continuous Conduction Mode,CCM)和DCM状态的小信号模型,在线性负载条件下,分析了CCM和DCM状态开环系统参数与补偿网络设计对于系统稳定性的影响,以及级联型ASI直流母线电压在空载状态下低频振荡产生的原因及其与环路参数的关系。针对后级变换器空载以及轻载状态,兼顾 CCM状态的稳定性和动态性研究分析总结了前级直-直变换器电路参数和补偿网络设计规则。
1 前级直-直变换器的小信号建模
零电压开关移相全桥(Zero-Voltage Switching-Phase Shifted Full Bridge,ZVS PSFB)直-直变换器拓扑利用隔离变压器的漏感和谐振电感共同与桥臂开关管源漏极寄生电容谐振,实现桥臂主开关管的零电压开通,具有控制方式简单可靠、高效率和高功率密度的优点[10,11]。同时实现了前后级的电气隔离,是作为级联型ASI前级DC-DC隔离变换器的理想选择。相比较单电压环控制策略,采用平均电流控制的零电压移相全桥变换器通过引入平均电流控制方式作为控制内环,配合电压外环,获得了更好的动态性能,并实现了短路限流保护。

图1 移相全桥直-直变换器主电路拓扑Fig.1 Main circuit of phase-shift full bridge DC-DC converter
假设ui为输入直流电压,ii为输入直流电流,uo为输出电压,io输出电流,d为占空比控制信号。电压、电流及占空比均可用其稳态分量和交流小信号分量之和来表示将和看作输入量,而、为输出量,主电路频域内的小信号模型可表示为

式中,A(s)为输入-输出电压开环传递函数;Zo(s)为开环输出阻抗;Gud(s)为占空比-输出电压传递函数;Yi(s)为开环输入导纳;Ai(s)为输出-输入电流开环传递函数;Gdi(s)为控制-输入电流传递函数。
移相全桥变换器可以等效为一种特殊的 Buck电路,由于漏感与谐振电感的引入,造成了占空比的丢失,所以移相全桥变换器的小信号模型又不同于传统的Buck变换器[12]。图2a为移相全桥直-直变换器等效小信号模型。图2a中n为移相全桥直-直变换器变压器一次、二次匝比;Re、Rc分别为滤波电感及滤波电容等效串联电阻,为直-直变换器输入电压小信号分量,为占空比小信号分量,为滤波电感电流变化导致占空比变化量,为输入直流电压变化导致占空比变化量,假设为移相全桥直-直变换器有效占空比交流小信号分量,Deff为其稳态分量,可得

平均电流控制型移相全桥直-直变换器控制框图如图2b所示。当工作在CCM模式下时,定义图2b中占空比-输出电压传递函数Gud1(s)、占空比-输出电感电流传递函数Gdi(s)、电流环开环传递函数Ti(s)、电压环开环传递函数Tv(s)、电流环采样系数Ki(s),电流环补偿网络传递函数Gi(s),控制信号-占空比 PWM 调制传递函数Gm(s),输出电压采样系数Kv(s),电压环补偿网络传递函数Gv(s),输入电压扰动对输出电压传递函数A(s),得到电流环补偿前后开环传递函数为


图2 移相全桥直-直变换器小信号模型及控制框图Fig.2 The small-signal model and control block of phase-shift full bridge DC-DC converter
小信号模型中各传递函数为

式中,Llk为变压器漏感;fs为主功率管开关频率;He(s)为输出 LC滤波器及负载构成的网络传递函数;Zf(s)为输出LC滤波器及负载构成的网络输入阻抗值。
移相全桥直-直变换器断续工作状态与连续工作状态的控制框图是一致的。传递函数中占空比-输出电压传递函数不同于电流连续模式[12],假设DCM状态下占空比-输出电压传递函数为Gud2(s)
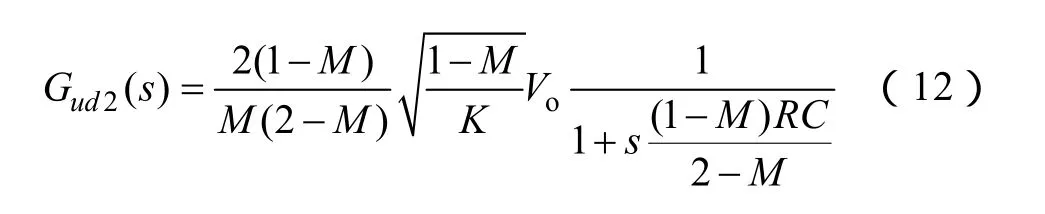
其中
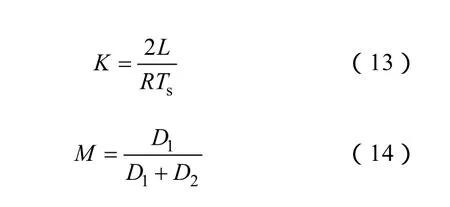
式中,D1为DCM状态一个开关周期中电感电流上升沿时间;D2为电感电流下降沿时间。
当ASI工作在空载DCM状态时,DC-DC变换器的负载为后级负载逆变器的空载损耗。
2 控制环路的设计
对于ASI变换器系统,瞬态性能指标主要有稳定性、动态性和抗扰性。稳定性则主要反映在相位裕度和幅值裕度上。通常相位裕度一般大于 45°,幅值裕度一般大于6dB[13]。动态性能则主要体现在系统开环截止频率上,截止频率越大,动态响应越快,但是截止频率同时受到开关频率的限制,以消除系统中有开关引起的高频成分。
对于采用平均电流控制的双环 DC-DC变换器而言,电压环截止频率往往远小于电流环截止频率,以获得良好的动态特性[14]。采用如图3所示的单极点单零点的补偿网络分别对电压环和电流环进行环路设计。该补偿网络在低频处补偿第一个极点,以消除稳态误差,并在变换器开关频率处补偿高频极点以衰减由开关工作造成的高频开关纹波,同时在控制对象传递函数的最低极点或以下补偿一个零点,以补偿由这个最低极点引起的相位滞后。

图3 单极点单零点补偿网络示意图Fig.3 Single pole and single zero compensation network

设置补偿网络的增益以满足电流内环具有合适的穿越频率。由于电流内环需要良好的动态特性,以期能跟踪电压外环的输出,因此电流内环需要较大的带宽。式(15)为该补偿网络传递函数。补偿网络的直流增益K=R2/R1,零点角频率为ωzi=1 /(R2C2),极点角频率ωpi=1 /(R2C1) 。
根据式(5)得到CCM模式下电流内环补偿前后的传递函数。利用Matlab软件绘制幅相曲线验证设计结果的正确性。Matlab模型参数根据实验室搭建的4kV·A样机进行设置。前级为平均电流控制移相全桥直-直变换器,后级为三相四桥臂逆变器。前级输入电压为 240~300V,直流母线电压为290V,直-直变换器变压器一次、二次侧匝比为6∶10,漏感为 3µH,开关频率为 100kHz,输出滤波电感Lf为 100µH,输出滤波电容Cf为300µF,电压采样系数Kv为3/300,电流采样系数Ki为0.093,PWM调制载波峰峰值为 2.35V,则调制信号对占空比传递函数

电流内环补偿前后幅相曲线如图4a所示。经过Gi(s)补偿后,提高了低频段的增益,截止频率设置在4.5kHz,同时相位裕度为110°,大于45°,满足稳定性要求。根据式(11),电压外环补偿前后的幅相曲线如图4b所示。为了提高系统的稳态性能,经过补偿后将截止频率设置在1kHz,相位裕度为110°,大于 45°,并且提高了中频段的增益,满足稳定性和动态性要求。


图4 CCM状态幅相曲线Fig.4 Gain and phase bode plots of transfer function when converter working in CCM mode
对直-直变换器负载为4kW、3kW、2kW和1.5kW四种 CCM 负载状态下所对应的电压环开环传递函数幅相曲线进行绘制,如图4c所示随着负载的降低,低频段增益不断提高,低频段相位逐渐降低。同时补偿网络参数能够在 CCM状态下全负载范围满足稳定性和动态性要求。
3 空载直流母线振荡及其抑制
当级联型变换器工作在空载状态时,前级DC-DC变换器负载为后级变换器的空载损耗,假设后级变换器空载损耗为100W,空载时前级DC-DC变换器等效于工作在 DCM模式。当平均电流控制移相全桥变换器工作在DCM状态时,采用与CCM状态时相同参数的补偿网络参数。根据式(12)~式(14),并结合式(11),推导得到电压电流双环补偿后的系统开环传递函数为

结合式(4)~式(11)得到空载状态下传递函数Tv(s)的奈奎斯特曲线如图5所示。并绘制如图6所示传递函数Tv(s)的幅相曲线。
根据 Nyquist判据,反馈控制系统稳定的充分必要条件是Nyquist曲线不穿过(-1,j0)点的圈数Rw等于开环传递函数的正实部极点数Pw。由图5可得传递函数Tv(s)的Nyquist曲线闭合包围(-1,j0)点的圈数Rw=0,同时计算Tv(s)极点为0、-499 895、-93 454/3、-22 350/13、-5 831/583、-1 373/774,不存在右半平面的极点,满足Rw=Pw=0,则补偿后系统在电流断续状态下是稳定的。

图5 空载时传递函数Tv(s)奈奎斯特曲线Fig.5 Nyquist curve plots of transfer function Tv(s)under no-load
如图6所示,当环路开环增益为 1(幅频曲线穿越频率处)时,对应相位小于-135°。所以当系统工作在轻载或空载状态下时,虽然针对电流连续模式设计的补偿网络能够在 CCM 模式下满足变换器系统的稳定性和动态性要求,且在 DCM模式下系统是稳定的,由于低频段在增益为0dB处存在相位小于-135°的频率点,不能满足相位裕度大于45°的要求,容易在实际系统延时的作用下使增益为0dB频率段的相位小于-π,此时满足自激振荡的两个条件:①幅频曲线振荡频率点增益为 0dB;②相频曲线振荡频率点相位低于-π。

图6 空载时传递函数Tv(s)幅频和相频特性曲线Fig.6 Gain and phase Bode plots transfer function Tv(s)under no-load
从而在该频率产生等幅正反馈现象造成自激,引起直流母线电压的低频脉动。
该低频脉动将降低后级变换器的输出波形质量。同时如图7所示,相频特性曲线中正反馈频率段相位和变换器负载的降低而下降(图7中四组曲线负载电阻分别为200Ω、400Ω、600Ω和800Ω,输出电压为300V),由图7可见自激振荡频率点随着负载的降低而缓慢下降。

图7 DCM模式下不同负载电压环补偿后幅频和相频特性曲线Fig.7 Gain and phase Bode plots of transfer function Tv(s)when converter working in DCM mode with different load
不同直流母线电容容值对应的Tv(s)传递函数伯德图如图8所示。图8中随着直流母线电容的增加,正反馈频率不断下降,且反馈深度随之加深,振荡幅值将随之增大。增加电容容量会使振荡频率降低振荡幅值增大,振荡频率为系统开环小信号传递函数Tv(s)幅相曲线的穿越频率。

图8 DCM模式下不同输出电容对应电压环补偿后幅频和相频特性曲线Fig.8 Gain and phase Bode plots of transfer function Tv(s)when converter working in DCM mode with different DC bus capacitor
不同电压环增益对应Tv(s)传递函数伯德图如图9所示。随着电压环增益的提高,低频段相位随之上升,直至增益为0dB的频率点对应的低频段相位高于-π,若考虑系统的延迟,参考 CCM 状态下相位裕度要求,该相位为高于-135°为宜。最终通过消除正反馈并抑制了直流母线电压振荡。

图9 DCM模式下不同电压环增益对应幅频和相频特性曲线电压环补偿后幅频和相频特性曲线Fig.9 Gain and phase Bode plots of transfer function Tv(s)when converter working in DCM mode with different voltage gain
若后级变换器为具有带不平衡负载能力的三相逆变器,根据文献[15,16]采用双重傅里叶积分法分析后级负载逆变器对直流母线谐波成分的影响,当负载出现不平衡状态时,直流母线电流中存在两倍逆变器输出基波频率的二次谐波含量,且大于或等于直流分量,当逆变器输出为400Hz时(机载静止变流器的输出通常为中频),该成分为800Hz。这就造成级联型变换器比传统负载平衡的逆变器需要更大的直流母线电容[17,18],根据上述对空载低频振荡机理的分析,此时需要相应提高前级的电压环增益。
级联型变流器前级直-直变换器生成稳定的直流母线电压,同时在前级功率等级允许的条件下该直流母线能够给多台后级变换器同时供电,增加的后级变换器中的输入电容将等效为增大直流母线电容容值,在系统负载较轻时同样会引起直流母线低频振荡。如果前级变换器环路设计不当同样会使低频脉动现象更加严重。
为了消除空载低频振荡,随着母线电容的增加需要提高前级电压环增益以提高变换器在 DCM状态下的动态性能。其设计原则是预测后级变换器输入滤波电容的裕量大小,并建立前级变换器小信号模型,在最小负载状态下,设计补偿网络使系统开环传递函数幅相曲线中截止频率所对应相位大于-180°,同时保证该传递函数奈奎斯特曲线闭合(-1,j0)点圈数等于正实部极点数以保证系统稳定性。同时过高的电压环增益,会提高系统开环截止频率,不利于滤除电压环输入信号的高频扰动,此外其也会降低系统的下垂特性,造成启动过程中过大的超调量造成输出电压瞬态过压。因此在满足抑制DCM状态母线电压自激振荡的情况下不宜过多的提高电压环增益。
4 仿真与实验验证
采用Saber仿真对上述分析结果进行仿真验证,仿真参数同 Matlab绘制伯德图所采用参数一致。仿真结果如图10和图11所示。
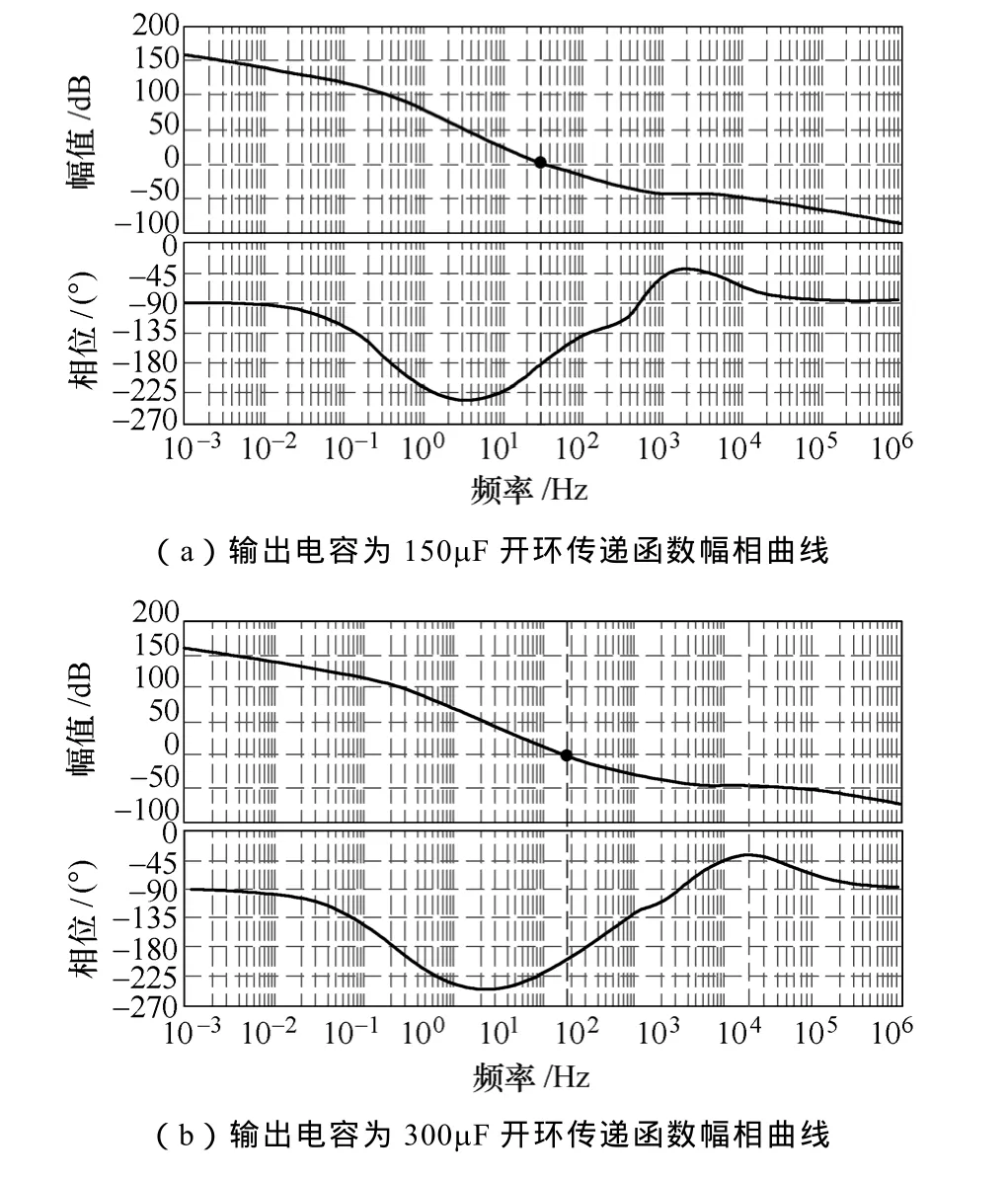
图10 不同容值幅相曲线Fig.10 Gain and phase Bode plots of transfer function Tv(s) with different DC bus capacitor


图11 仿真波形Fig.11 Simulation waveforms
图10a和图10b分别为直流母线电容 150μF与300μF空载时系统开环幅相曲线,两种容值下自激振荡频率点分别为29Hz与17Hz。
如图11a与图11b中,在直流母线电容为150μF、300μF,电压环增益与Matlab绘制图10幅相曲线时一致,为12dB。所对应输出电压自激振荡频率分别为26Hz与13Hz,与图10中幅相曲线截止频率值基本吻合。低频振荡幅值随着母线电容的增加而增加,同时频率随着母线电容的增大而降低。
依据本文所提供的设计依据重新定义补偿网络参数,提高电压环增益为35dB后的直流母线电压启动波形如图11c所示,此时直流母线电容为300μF。仿真结果证明本文的得到的设计依据对于抑制空载自激振荡是有效的。
为了验证本文的环路设计原则,在实验室制作一台4kV·A两级式航空静止变流器,主电路拓扑和参数与Matlab以及Saber仿真参数一致。
图12a所示为设置实验平台电压环增益为6dB,直流母线电容为150μF时的实验波形。在环路参数优化设计之前,直流母线空载状态出现频率约为22Hz的低频振荡,振荡峰峰值约为40V。若后级变换器为输出 115V/400Hz三相逆变器,当直流母线电压脉动到波谷处时,后级逆变器因为输入电压过低造成波峰处的过调制导致输出电压畸变,输出正弦波叠加低频脉动成分,脉动频率等于直流母线电压振荡频率,逆变器输出波形中的低频脉动成分如图12a虚线所标识。


图12 实验波形Fig.12 Experimental waveforms
保持直流母线电容为150μF,提高电压环增益为30dB后,级联型变流器直流母线电压与后级逆变器三相输出电压在空载工作模式下启动和稳态工作时的波形如图12b和图12c所示。参考本文所总结的设计依据设计补偿网络参数,能够抑制图12a中ASI空载直流母线低频振荡,并实现系统空载状态下的动态性能和稳态性能。
5 结论
本文在前级平均电流控制移相全桥直-直变换器CCM与DCM状态小信号模型的基础上,分析了两级式变换器直流母线空载低频脉动是由于补偿网络增益不足造成的,归纳了适用于级联型变换器,同时兼顾CCM与DCM模式稳定性、动态性的补偿网络设计方法。最终本文通过仿真和实验验证了分析结果的正确性,得到以下结论:
(1)采用平均电流控制的移相全桥直-直变换器空载模式下经过双环补偿网络矫正,因为开环传递函数相频特性曲线低频段的正穿越与负穿越次数相等,则需要根据开环传递函数是否包含正实部极点判断系统稳定性。当校正后系统是稳定的,若补偿网络设计不当开环传递函数伯德图截止频率处对应相位小于-π,该频率处的正反馈造成系统自激,将导致直流母线空载低频振荡,后级输入电容对前级稳定性有较大影响,尤其是在轻载条件下。
(2)提高直流母线电容会导致振荡频率下降,正反馈深度加深。此时自激振荡频率下降,振荡幅值提高,对提高后级负载逆变器输出波形质量不利。
(3)提高电压环增益能够提高低频正反馈频率的相位,有效抑制低频振荡。为了抑制由后级逆变器负载不平衡引起的直流母线800Hz的低频脉动,直流母线容值相对于平衡负载的级联型变流器容值更大,需要提高电压环增益以抑制低频段正反馈造成的电压脉动。
[1]张方华,龚春英.高效率模块化航空静止变流器的研制[J].航空学报,2009,30(6): 1119-1125.
Zhang Fanghua,Gong Chunying.High efficiency modular aeronautic static inverter[J].Acta Aeronautica et Astronautica Sinica,2009,30(6): 1119-1125.
[2]葛红娟,蒋华,王培强.基于内模原理的新型三相航空静止变流器闭环控制系统[J].电工技术学报,2006,21(9): 88-92.
Ge Hongjuan,Jiang Hua,Wang Peiqiang.A novel three-phase aviation static inverter closed loop control system based on the internal mode principle[J].Transactions of China Electrotechnical Society,2006,21(9):88-92.
[3]Liu Changrong,Lai Jihsheng.Low frequency current ripple reduction technique with active control in a fuel cell power system with inverter load[J].IEEE Transactions on Industry Electronics,2007,22(4):1429-1436.
[4]Junichi Itoh,Fumihiro Hayashi.Ripple current reduction of a fuel cell for a single-phase isolated converter using a DC active filter with a center tap[C].IEEE Transactions on Power Electronics,2010,25(3): 550-556.
[5]朱成花,严仰光.一种改进的阻抗比判据[J].南京航空航天大学学报,2006,38(3): 315-320.
Zhu Chenghua,Yan Yangguang.Improved impedance criterion[J].Journal of Nanjing University of Aeronautics& Astronautics,2006,38(3): 315-320.
[6]Feng X G,Liu J J,Lee F C.Impedance specifications for sTableDC distributed power systems[J].IEEE Transactions on Power Electronics,2002,17(2):157-162.
[7]Wu Tao,Ruan Xinbo.Standardization of input/output impedance specifications of Buck converters based on the system integration cencept[C].Power Electronics and Motion Control Conference,2006: 1-6.
[8]王建华,张方华,龚春英,等.电压控制型 Buck DC/DC变换器输出阻抗优化设计[J].电工技术学报,2007,22(8): 18-23.
Wang Jianhua,Zhang Fanghua,Gong Chunying,et al.Study of output impedance optimization for voltage mode control Buck DC/DC converter[J].Transactions of China Electrotechnical Society,2007,22(8): 18-23.
[9]吴涛,阮新波.分布式供电系统中负载变换器的输入阻抗分析[J].中国电机工程学报,2008,28(12): 20-25.
Wu Tao,Ruan Xinbo.Input impedance analysis of load converters in the distributed power system[J].Proceedings of the CSEE,2008,28(12): 20-25.
[10]Song Tingting,Huang Nianci.A novel zero-voltage and zero current switching full bridge PWM converter[J].IEEE Transactions on Power Electronics,2005,20(2): 286-291.
[11]Ruan Xinbo.An improved ZVS PWM full-bridge converter with clamping diodes[C].Annual IEEE Power Electronics Specialists Conference,2004: 1476-1481.
[12]Cho Junggoo,Baek Juwon,Chang Yong Jeong,et al.Novel zero-voltage and zero-current-switching fullbridge PWM converter using a simple auxiliary circuit[J].IEEE Transactions on Industry Applications,1999,35(1): 15-20.
[13]储仁杰,贲洪奇,吴辉.FB-ZVZCS变换器小信号建模及补偿器设计[J].控制工程,2008,15(3): 302-309.
Chu Renjie,Ben Hongqi,Wu Hui.Small-signal modeling of FB-ZVZCS converter and compensator design[J].Control Engineering of China,2008,15(3):302-309.
[14]王艳丹,蔡宣三.全桥零电压开关-脉宽调制变换器的小信号分析与最优控制[J].清华大学学报,1994,34(4): 52-61.
Wang Yandan,Cai Xuansan.Analysis and optimum control of ZVS full-bridge PWM converter[J].Journal of Tsinghua University,1994,34(4): 52-61.
[15]陈仲,汪昌友,陈森.航空静止变流器的输入纹波电流特性研究[J].中国电机工程学报,2012,32(27):154-161.Chen Zhong,Wang Changyou,Chen Sen.Analysis on input ripple current characteristics of aviation static inverters[J].Proceedings of the CSEE,2012,32(27):154-161.
[16]Di Zhang,Fei(Fred)Wang,Rolando Burgos,et al.Common-mode circulating current control of paralleled interleaved three-phase two-level voltage-source converters with discontinuous space-vector modulation[J].IEEE Transactions on Power Electronics,2011,26(12): 3925-3935.
[17]Dahono P A,Kataoka T.Analysis and minimization of ripple components of input current and voltage of PWM inverters[J].IEEE Transactions on Industry Applications,1996,32(4): 945-950.
[18]Evans P D,Hill Cottingham R J.DC link current in PWM inverter[J].Proceedings of IEEE,1986,133(4):217-224.
