基于耦合电感倍压单元的零输入电流纹波高增益非隔离变换器

陈章勇 许建平 吴建雪

（1.西南交通大学电气工程学院 成都 610031

2.西南交通大学磁浮技术与磁浮列车教育部重点实验室 成都 610031）

0 引言

高增益升压变换器[1-3]已经广泛应用于工业领域，如在不间断电源系统中，需要将铅酸蓄电池的低输出电压转换为逆变器的380V直流输入电压。光伏、燃料电池等新能源系统同样需要具有高升压变比的直-直变换器。

为了满足高增益升压要求，传统Boost变换器需工作在接近于1的大占空比状态。但是，Boost变换器电路中元器件寄生电阻的存在，限制了它的升压增益；同时，当Boost变换器工作在接近于1的大占空比状态时，Boost变换器的效率较低。此外，Boost变换器的开关管电压应力钳位在输出电压，在高输出电压应用场合，需要选取高电压等级、导通电阻较大的MOSFET，从而增加了变换器电路成本和开关管的导通损耗，降低了变换器的效率。

为了解决传统Boost变换器面临的上述问题，国内外已有大量文献[4-17]提出了相应的解决方案。在传统Boost变换器基础上，通过增加开关电容[4,6]和开关电感[5]电路网络，可以提高变换器的升压比，但是升压比越高，需要采用的电路网络单元越多，增加了变换器的成本；文献[7-9]采用拓扑级联方式实现了变换器的高升压增益，但级联变换器导致变换器的效率较低；文献[10]提出的组合拓扑高增益Boost变换器采用交错控制，增加了成本且升压比有限，仅为传统Boost变换器增益的两倍；文献[11-15]提出的变换器组合耦合电感技术和开关电容技术，实现了高增益输出，但漏感的存在带来了开关管两端的电压尖峰，采用有源钳位技术[16]或无源吸收电路[16,17]可减小电压尖峰，却增加了变换器的控制复杂度。

此外，对于光伏、燃料电池等新能源应用场合，较大的脉冲电流会影响其寿命，甚至损坏发电设备[18,19]。目前为止，已有大量文献研究了低输入电流纹波开关变换器[2,20-22]。文献[2]以两相交错并联的方式减小了输入电流纹波，但增加了变换器的成本和控制复杂度；文献[20]提出的高增益变换器拓扑，通过选取特定的开关管占空比，消除了输出电流纹波，但该变换器需要两个开关管，增加了变换器的控制复杂度；文献[21]提出的变换器输入电流连续，但为了减小输入电流纹波，需要选取较大的输入电感，从而增加了变换器的体积，降低了动态响应速度；文献[22]提出如图1所示的零输入电流纹波Boost变换器，已成功应用于功率因数校正领域，该变换器在Boost变换器单元的基础上，增加分立电感La和中间储能电容C1，实现变换器的输入电流零纹波，简化了输入滤波器的设计。

图1 零输入电流纹波Boost变换器Fig.1 Zero input current ripple Boost converter

基于以上研究，本文提出了一种零输入电流纹波高增益非隔离型DC-DC变换器，采用电感耦合技术实现了高升压增益特性。为了解决漏感带来的开关管电压尖峰，采用由二极管和电容组成的无源无损吸收电路为漏感提供释放能量支路，将开关管电压钳位，从而降低了开关管的电压应力。另外，为了进一步解决输出二极管寄生电容与一次漏感造成的电压振荡，在变换器拓扑中引入耦合电感倍压单元，不仅降低了开关管和二极管的电压应力，同时保证了变换器的高升压增益特性。因此，可以通过选取低电压应力、低导通电阻的MOSFET，降低开关管的导通损耗，提升变换器的效率。本文分析了该变换器的工作原理和工作特性，最后，通过实验验证了理论分析的正确性。

1 工作原理分析

1.1 电路拓扑

图2a为基于耦合电感倍压单元的零输入电流纹波高增益变换器，其等效电路如图2b所示，其中，耦合电感由漏感Ls、电感L1、电压比为np∶ns的理想变压器构成，np∶ns=1∶n。二极管VDc和电容Cc组成无源无损吸收电路，在开关管关断时，吸收漏感能量，将开关管的电压应力钳位在电容电压VCc。二极管VD1、电容C2和耦合电感L1、L2组成耦合电感倍压单元电路，用于提升变换器的增益并减小开关管S1和二极管VDo两端的电压应力。C1为中间储能电容，VDo为输出二极管，Co为输出滤波电容，Ro为等效负载电阻。为简化分析，假设：

（1）除反并联二极管VDs1与寄生电容Cs1外，认为开关管S1是理想的且二极管VD1、VDo为理想器件。

（2）电容C1、C2和Co上的电压保持恒定。

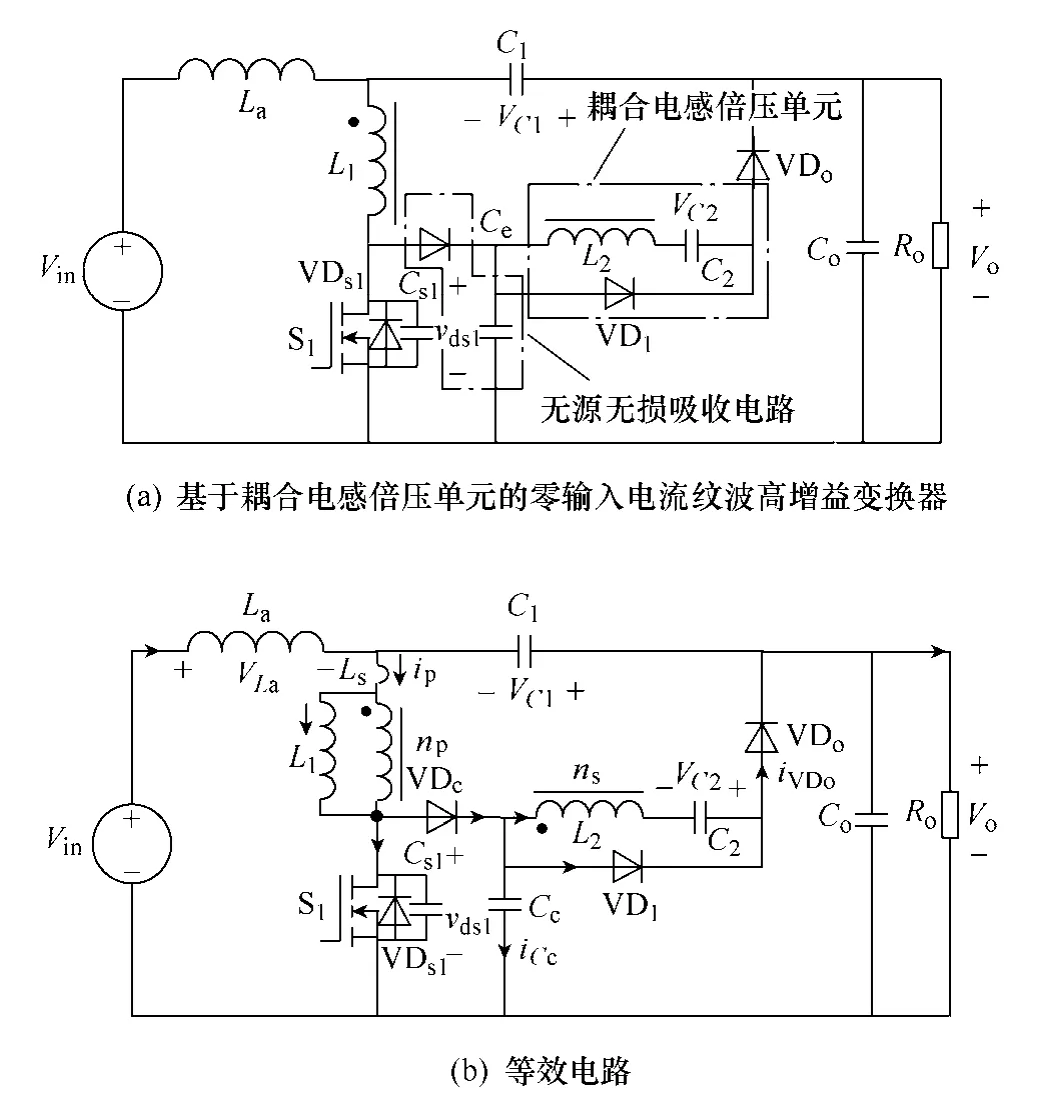
图2 零输入电流纹波高增益变换器Fig.2 Zero input current ripple high voltage gain converter

1.2 工作模态分析

在一个开关周期内，变换器存在如图3所示的 7种工作模态，变换器的主要工作波形如图4所示。在开关周期开始时刻，励磁电感电流im＞0，输出二极管VDo提供续流支路。

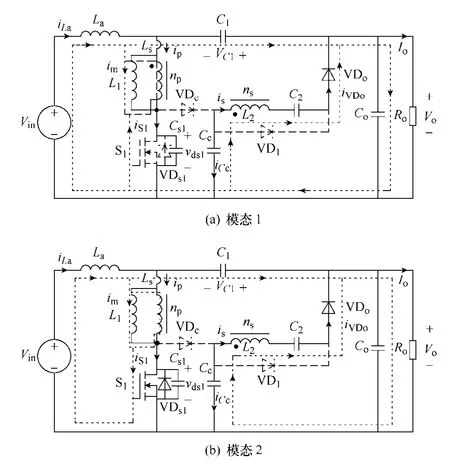
图3 变换器工作模态及等效电路Fig.3 Operation mode of the proposed converter

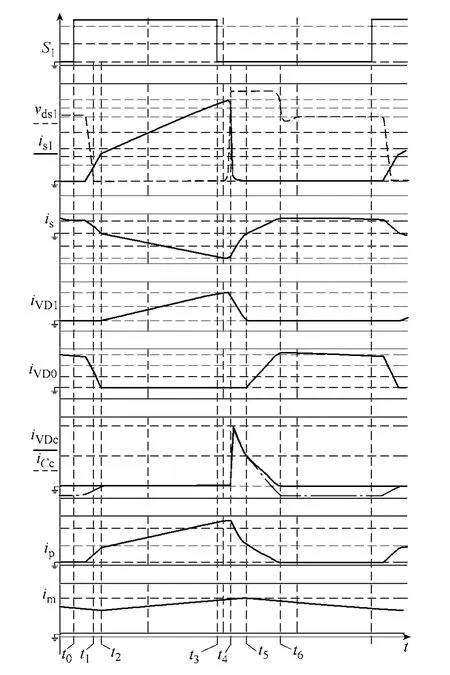
图4 变换器的主要工作波形Fig.4 Typical waveforms of the proposed converter

模态1[t0～t1]：t0时刻，开关管的驱动脉冲到来，开关管的寄生电容放电，输出二极管VDo导通，为励磁电感电流im提供续流通路。吸收回路二极管VDc关断，电容Cc和C2通过二极管VDo向负载传递能量，输入电感La通过电容C1向负载传能。

模态2[t1～t2]：t1时刻，开关管S1寄生电容放电完毕，开关管S1导通。此时，流过二极管VDo的电流还未降到0，二极管VDo继续导通。当二极管VDo电流下降到0时，此工作模态结束。

模态3[t2～t3]：t2时刻，流过二极管VDo的电流iVDo下降到0，二极管VDo实现零电流关断。此时，耦合电感的二次电流is下降到0并继续下降，二极管VD1为提供流通路径而导通，一次电压被钳位在电容电压VC2，电感电流im线性上升

式中，n为变压器电压比。流过漏感的电流ip等于流过开关管S1的电流iS1

耦合电感二次电流is为

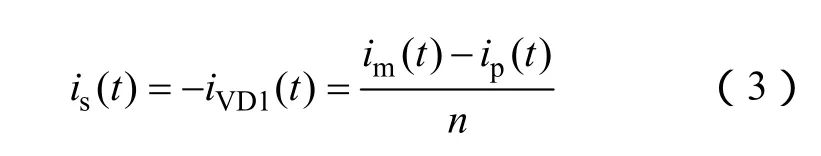
模态4[t3～t4]：t3时刻，开关管S1关断，耦合电感一次侧的漏感电流ip与开关管S1的寄生电容谐振充电，二次电流is继续流过二极管VD1。当开关管S1的电压上升到最大电压应力时，流过开关管的电流iS1变为0，此工作模态结束。

模态5[t4～t5]：t4时刻，开关管S1的寄生电容充电完毕，此时漏感上存在较大的能量，为提供漏感电流ip的流通通路，二极管VDc导通，漏感电流ip对电容Cc充电。此时，漏感电流ip线性下降

电感L1两端电压被钳位在电容电压VC2/n，电感电流im继续线性上升，因此流过耦合电感的二次电流is迅速下降。当流过二极管VD1的电流iVD1下降到0时，此工作模态结束。

模态6[t5～t6]：t5时刻，二极管VD1的电流iVD1下降到0，二极管VD1实现零电流关断，消除了二极管VD1的反向恢复损耗。此时，耦合电感的二次电流is上升到0并继续上升，输出二极管VDo为提供其流通路径而导通。漏感电流ip继续通过二极管VDc向电容Cc释放能量。变压器二次电压被钳位在VCc+VC2-Vo，电感电流im线性下降

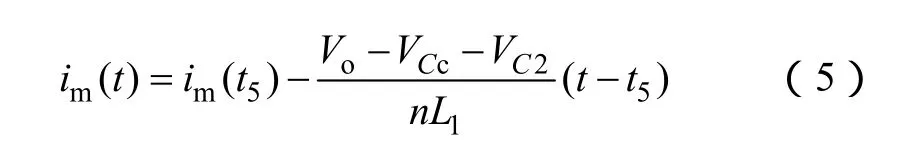
漏感电流ip线性下降

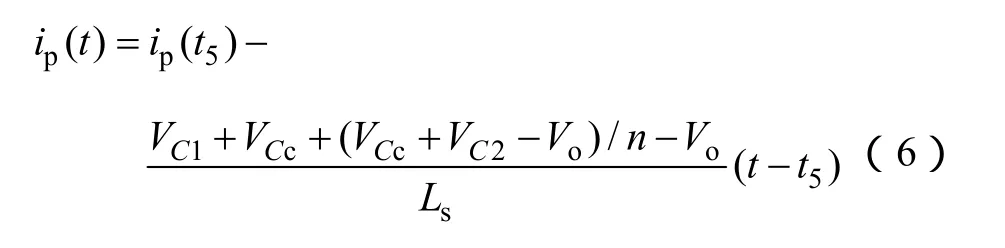
当漏感电流ip下降到0时，此工作模态结束。

模态7[t6～t7]：t6时刻，漏感电流ip下降到0，二极管VDc实现零电流关断，消除了二极管VDc的反向恢复损耗。此时，电容Cc与电容C2串联，通过二极管VDo向负载传递能量。一次侧励磁电感通过二次侧电感、二极管VDo、电容Cc和C2续流，电感电流im继续线性下降，直到下一个开关周期驱动脉冲的到来，开始下一个开关周期。

2 工作特性分析

2.1 零输入电流纹波特性分析

在一个开关周期内，输入电感La、中间储能电容C1与输出电容Co组成一个电压回路，由KVL方程，可知输入电感La两端的电压为

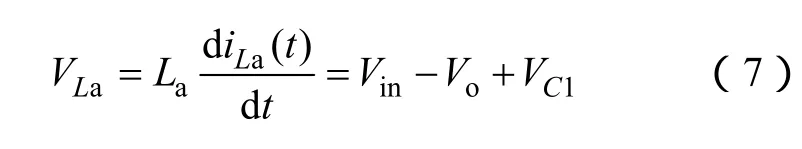
只要中间电容C1和输出滤波电容Co选取足够大，在一个开关周期内其纹波电压较小，可以认为是恒定不变的。此外，在一个稳态周期内，电感La满足伏秒平衡，即电感两端电压在一个周期内的平均值为零，故由式（7）可知中间电容电压为

式（8）是保证变换器输入零电流纹波的条件，它与其他电路参数无关且不受占空比限制[18]，仅使用了一个开关管，降低了变换器的成本。在设计变换器时，通过选取电容值较大的电容以减小电压纹波，从而较好地实现变换器的零输入电流纹波特性。

2.2 电压增益特性分析

由工作模态的分析可知，模态1、2和模态4、5工作时间较短，在进行稳态分析时可以忽略其影响，简化后的主要工作波形如图5所示，其中，D为开关管S1的导通占空比，VD1为二极管VDc的导通占空比，Ts为开关周期。考虑漏感对变换器增益影响，引入参量k=L1/(Ls+L1)。

图5 变换器的简化工作波形Fig.5 Simplified waveforms of the proposed converter

开关管S1导通阶段，电感L1与漏感Ls串联分压，可知励磁电感L1上的电压为

折算到耦合电感的二次侧，可得

由工作模态3可知，在开关管S1导通阶段，耦合电感的二次电压钳位在电容电压VC2，因此

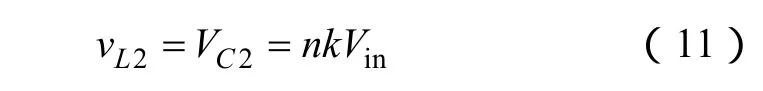
开关管S1关断阶段，如工作模态6所示，可得耦合电感一次电压

当开关管S1关断后，二极管VDc导通，为漏感电流ip提供续流通路，直到漏感能量释放完毕，如图5所示的二极管VDc导通时间段[DTs～(D+D1)Ts]。在此期间，漏感电流ip线性减小，流过输出二极管的电流iVDo线性增加，当二极管电流iVDo增加到与励磁电感电流im折算到二次侧的等效电流值相等时，漏感能量释放完毕，吸收回路二极管电流iVDc下降到0。在时间段[(D+D1)Ts～Ts]内，输出二极管电流iVDo等于电容Cc的电流iCc。在稳态周期内，电容Cc满足电荷平衡，由文献[16]的推导可知，吸收电路二极管VDc的导通占空比为

一个稳态周期内，开关管导通时间段内励磁电感两端的电压为VC2/n，开关管关断时间段内励磁电感两端的电压为(VCc+VC2-Vo)/n，由励磁电感L1的伏秒平衡，可知

联立式（8）、式（11）、式（12）和式（14），求解可得

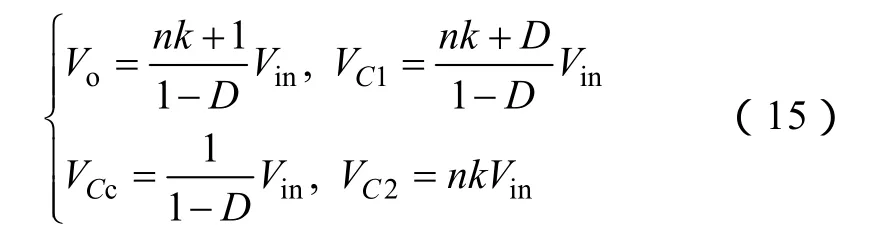
由此可得出变换器的增益特性表达式为

图6给出了参量k=1，不同变压器电压比n=1,3,5时，变换器增益随开关管占空比D的变化曲线，由图6可知，随占空比D和耦合电感电压比n的增大，变换器增益也随之增大。图7给出了变压器电压比n=3，参量k在0.9～1.0中间变化时，漏感对变换器增益特性的影响曲线，由图7可知，随着参量k的减小，即漏感Ls的增大，变换器的增益特性略有减小。

图6 变换器的增益曲线（k=1）Fig.6 Gain curves of the proposed converter at k=1

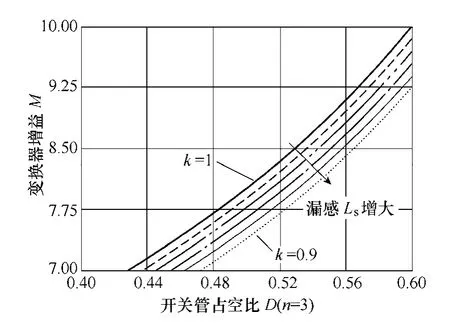
图7 变换器的增益曲线（n=3）Fig.7 Gain curves of the proposed converter at n=3

2.3 元器件的应力分析

由工作模态分析可知，开关管S1关断时，开关管电压钳位在电容电压VCc，可得开关管S1的电压应力为

开关管S1导通期间，二极管VDo关断，可得二极管VDo的电压应力

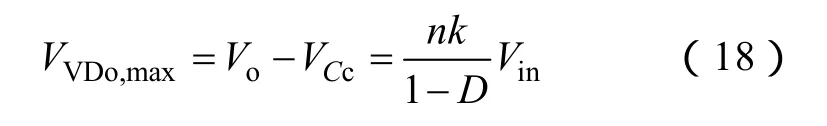
二极管VD1和二极管VDc的电压应力分别为

以输入电压Vin为归一化量，图8给出了变换器关键元器件的应力曲线。尽管元器件的电压应力与变压器电压比n有关，由图8可知，变换器中开关管S1和二极管VDc、二极管VDo和VD1、储能电容电压VC1、VC2和VCc的电压应力均小于输出电压Vo。然而，传统Boost变换器元器件的电压应力钳位在输出电压，高输出电压导致开关管和二极管的电压应力较高，增加了变换器的成本。同时，采用耦合电感倍压电路后，进一步提升了变换器的增益特性，可避免极限占空比的情况出现。因此，可通过选取低电压等级低导通电阻的MOSFET以减小开关管的导通损耗，通过选取低电压等级的输出二极管VDo以减小反向恢复损耗，在进一步提高变换器效率的同时，也降低了成本。由图8可知，随着占空比D和耦合电感电压比n的增大，开关器件的电压应力随着增大。因此，在设计变换器时，需权衡电压比n与增益特性之间的利弊。

图8 变换器元器件应力曲线（n=3,k=1）Fig.8 Stress analysis of the proposed converter at n=3 and k=1

2.4 性能对比分析

在不考虑漏感影响情况下，对本文所提出的变换器、传统Boost变换器和文献[12]提出的变换器进行了对比分析，见下表。由表可知，通过设计耦合电感电压比n，本文所提出的变换器可实现高升压增益特性，避免传统Boost变换器中接近于1的极限占空比情况的出现。同时，输出二极管和开关管的电压应力也相对较低，可选取低电压等级的开关管、二极管以减小开关损耗和反向恢复损耗。与传统Boost变换器和文献[12]提出的耦合电感Boost变换器相比，本文所提出的变换器以增加二极管和储能电容的数量为代价，基本上消除了输出二极管的反向恢复损耗。此外，本文所提出的变换器具有零输入电流纹波特性，可简化输入滤波器的设计，减小了变换器的体积与重量。

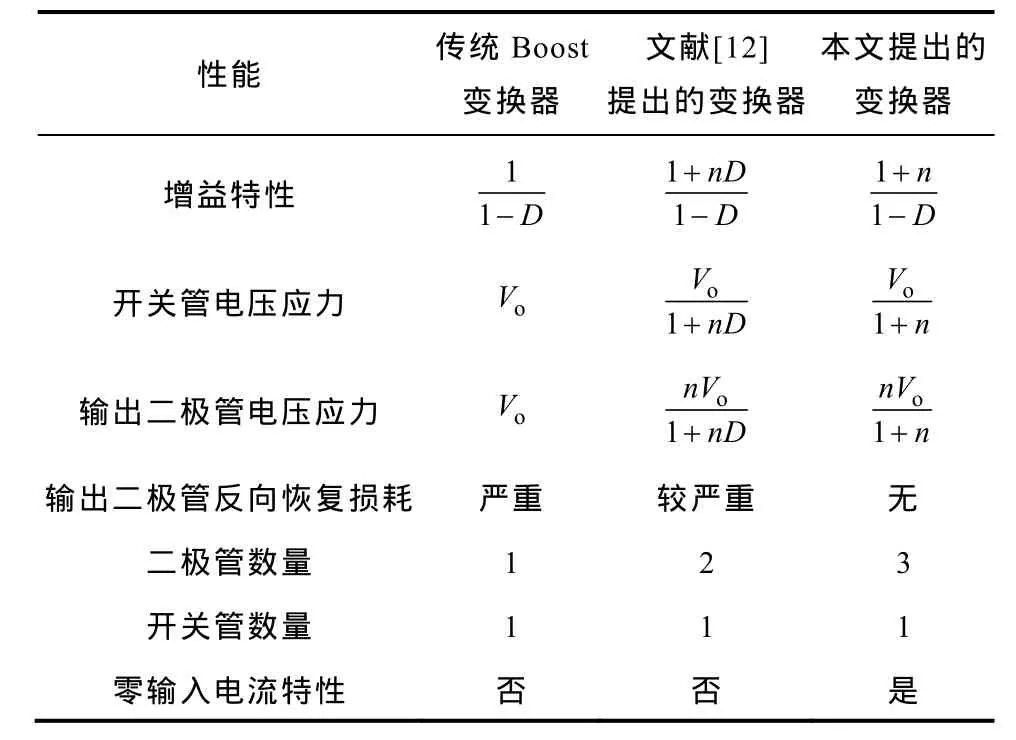
表工作特性对比分析Tab.Comparative anlysis of operating characteristics

3 实验

3.1 设计实例

为了验证理论分析的正确性，本文进行了实验验证，变换器的关键参数如下：输出功率Po=80W，输入电压Vin=24V，输出电压Vo=200V，输入电感La=50μH，储能电容C1=C2=Cc=4.7μF，输出滤波电容Co=220μF，开关频率fs=100kHz。

由变换器参数可知，变换器需要实现的升压比为Vo/Vin=200/24=8.33。设计变压器时使漏感保持在一次电感的5%以内，由于漏感的存在会带来增益的降低，耦合电感电压比过高会导致二极管电压应力增大，折中考虑并考虑一定的裕量，选取变压器电压比n=2.8，根据式（16）计算出所需的占空比D=0.56，耦合电感选取TDK公司的ETD34磁心，一次、二次匝比为14T∶40T，一次电感L1=40μH，由此可以计算出储能电容C1、C2上的电压分别为VC1=176V，VC2=72V，同时钳位电压Cc两端的电压为VCc=54.5V。由此可知，开关管S1和吸收二极管VDc的电压应力为54.5V，二极管VD1和VDo的电压应力为145V，考虑一定裕量，选取开关管S1型号STP19NF20（VDSS=200V，RDS(on)=0.16Ω），选取二极管VDc为电压等级为150V的肖特基二极管STPS3150，二极管VD1和VDo为电压等级为200V的快恢复二极管STTH302。

3.2 实验验证

如图9～图16所示为满载工作时，基于耦合电感倍压单元的零输入电流纹波高增益变换器的实验波形。图9为开关管S1两端电压和流过开关管电流的波形，虽然采取了吸收电路，可以抑制部分电压尖峰，但由于二极管VDc和开关管S1的寄生电容存在，漏感与寄生电容产生谐振，开关管两端仍存在一定的电压振荡，可以在二极管VDc两端增加吸收电路来进一步减小开关管的电压尖峰。图10所示为流过输出二极管VDo的电流波形及两端电压波形，由图10可知，采用倍压单元电路后，消除了二次侧漏感与二极管VDo的寄生电容产生的振荡现象，且二极管VD1的电压应力小于输出电压（Vo=200V），继而减小了二极管的电压应力。在开关管 S1关断时，漏感能量通过吸收电路中的二极管VDc释放，如图11所示为流过二极管VDc和电容Cc的电流波形，由图11可知，二极管VDc实现了零电流关断。图12为耦合电感一次、二次电流波形，可知在开关管S1关断时刻，一次电流ip开始减小，漏感释放能量，流过耦合电感二次侧的电流经过输出二极管VDo向负载传递能量；开关管导通阶段，二极管VD1导通，与理论分析一致。图13为输入电感电流iLa的实验波形，由图13可知，输入电感电流iLa几乎实现了零纹波特性。钳位电容电压VCc、输出电压Vo、中间电容电压VC1和储能电容VC2的实验波形分别如图14～图16所示，在输出电压Vo=200V时，测得钳位电容电压和中间储能电容电压为VCc=55V，VC1=176V，VC2=72V与理论计算值基本保持一致。

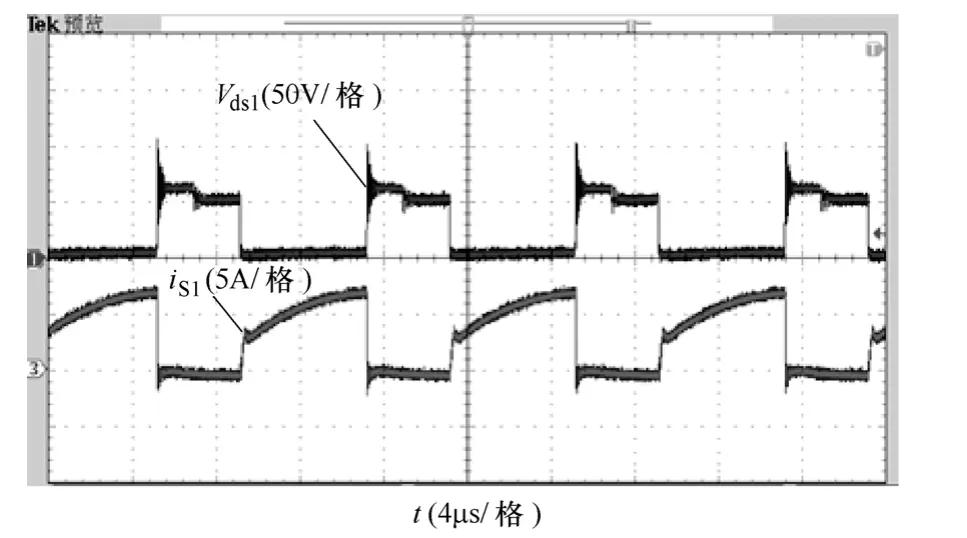
图9 开关管S1的漏源电压、电流波形Fig.9 Voltage and current waveforms of switch S1

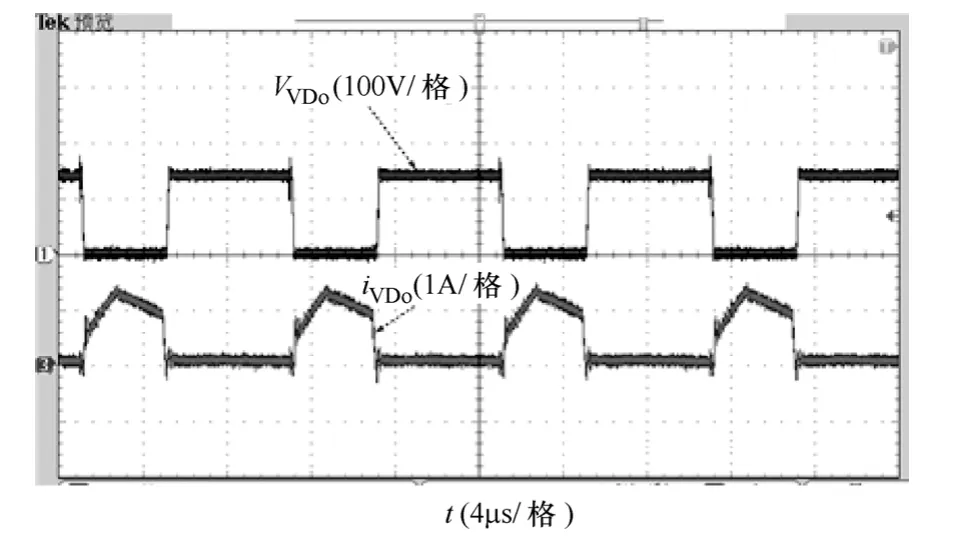
图10 二极管VD1两端电压及电流波形Fig.10 Voltage and current waveforms of diode VD1

图11 吸收电路的电流实验波形Fig.11 Voltage and current waveforms of passive lossless snubber

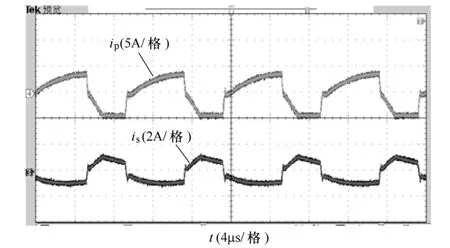
图12 变压器一次电流波形Fig.12 Primary current waveforms of the transformer

图13 输入电流波形Fig.13 Input current iLa waveform flowing through inductor La

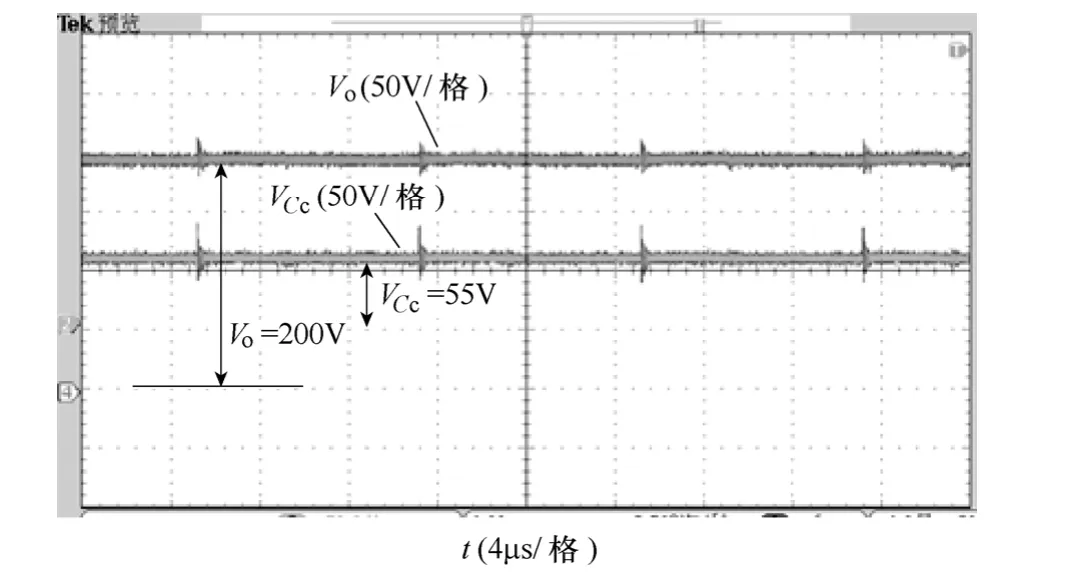
图14 输出电压与钳位电容电压波形Fig.14 Output voltage and clamped capacitor voltage waveforms

图15 中间储能电容电压波形Fig.15 Energy-storage capacitor voltage VC1 waveform

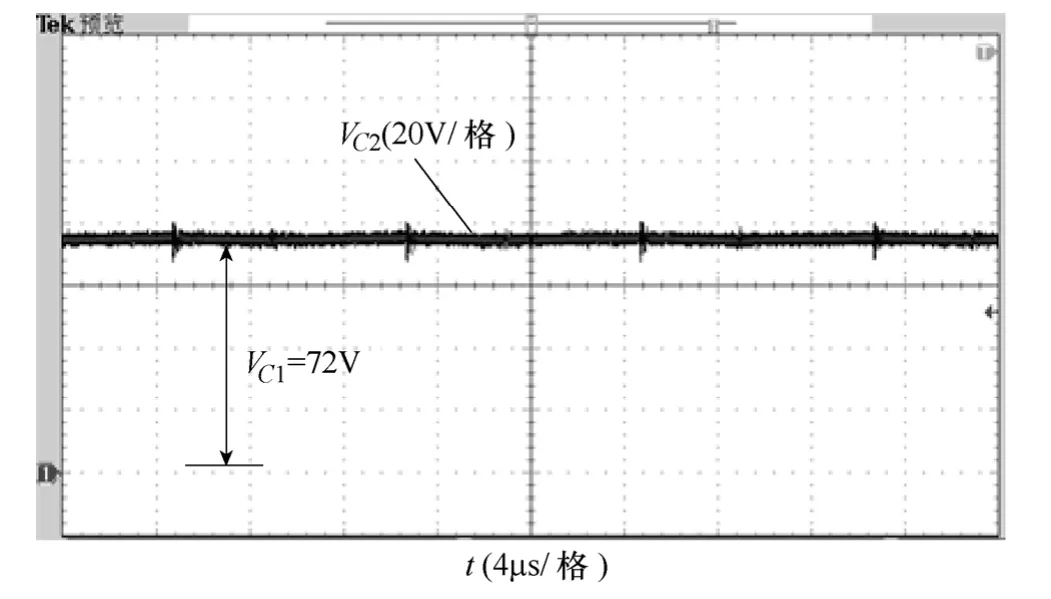
图16 电容C2两端电压波形Fig.16 Voltage waveform of capacitor C2

图17所示为本文提出的零输入电流纹波高增益变换器与文献[12]所提出的变换器的效率对比曲线，由图17可知，基于耦合电感电压单元的无源无损高增益零纹波变换器的最高效率可达到 94.5%，在满载Po=80W时，变换器的效率为94%。而文献[12]提出的基于耦合电感的 Boost变换器最高效率为 93.5%，其主要原因：①在相同耦合电感电压比的情况下，本文所提出的变换器可采用较小的开关管占空比，因此，提高了变换器的效率；②采用耦合电感倍压单元后，几乎消除了输出二极管VDo的反向恢复损耗，同时消除了耦合电感一次漏感与二极管寄生电容产生的振荡现象，从而减小了二极管的电压应力。此外，本文提出的变换器具有零输入电流纹波特性，减小了输入滤波器的设计难度。

图17 效率曲线Fig.17 Efficiency curves

4 结论

本文提出了一种耦合电感倍压单元零输入电流纹波高增益非隔离 DC-DC变换器，详细分析了变换器的工作原理及工作特性，搭建实验平台验证了理论分析的正确性。实验结果表明，变换器基本上实现了零输入电流纹波特性，而且采用耦合电感倍压单元后，通过合理设计耦合电感电压比，实现变换器的高增益特性。同时，变换器的开关管电压应力远小于输出电压，降低了开关管的电压应力。无源无损吸收电路有效吸收了漏感能量，基本消除了开关管两端的电压尖峰，将开关管电压钳位。此外，采用倍压单元消除了输出二极管寄生电容与二次侧漏感的寄生振荡现象，从而降低了输出二极管的电压应力，减小了反向恢复损耗。基于以上优点，该变换器非常适合于光伏、燃料电池等新能源应用场合。

[1]Chen S M,Liang T J,Yang L S,et al.A safety enhanced,high step-up DC-DC converter for AC photovoltaic module application[J].IEEE Transactions on Power Electronics,2012,27(4): 1809-1817.

[2]Lai C M,Pan C T,Cheng M C.High-efficiency modular high step-up interleaved Boost converter for DC-microgrid applications[J].IEEE Transactions on Industry Applications,2012,48(1): 161-171.

[3]Tseng K C,Tsai M H,Chan C Y.Design of high step-up conversion circuit for fuel cell power supply system[C].IEEE International Symposium on Next-Generation Electronics (ISNE),Kaohsiung,Taiwan,2013: 506-509.

[4]Ismail E H,Al-Saffar M A,Sabzali A J,et al.A family of single-switch PWM converters with high step-up conversion ratio[J].IEEE Transactions on Circuits and Systems,2008,55(4): 1159-1171.

[5]Axelrod B,Berkovich Y,Ioinovici A.Switchedcapacitor/switched-inductor structures for getting transformerless hybrid DC-DC PWM converters[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2008,55(2): 687-696.

[6]陆治国,郑路遥,马召鼎,等.带开关电容网络的交错并联高增益 Boost 变换器[J].电工技术学报,2012,27(11): 153-159.

Lu Zhiguo,Zheng Luyao,Ma Zhaoding,et al.Interleaved high gain Boost converter with switched capacitor network[J].Transactions of China Electrotechnical Society,2012,27(11): 153-159.

[7]Delshad M,Mohammadi S,Moosavi S.A new cascaded high step-up DC-DC converter[C].IEEE Electrical Engineering/Electronics,Computer,Telecommunications and Information Technology (ECTICON),Phetchaburi,Thailand,2012: 1-4.

[8]Yang P,Xu J,Zhou G,et al.A new quadratic Boost converter with high voltage step-up ratio and reduced voltage stress[C].IEEE Power Electronics and Motion Control Conference (IPEMC),Harbin,China,2012,2: 1164-1168.

[9]张士宇,许建平,杨平.新型单开关高增益 Boost变换器研究[J].电工电能新技术,2013,32(3): 13-15.

Zhang Shiyu,Xu Jianping,Yang Ping.Research on a new single-switch high gain Boost converter[J].Advanced Technology of Electrical Engineering and Energy,2013,32(3): 13-15.

[10]罗全明,闫欢,孙明坤,等.基于拓扑组合的高增益Boost变换器[J].电工技术学报,2012,27(6): 96-102.

Luo Quanming,Yan Huan,Sun Mingkun,et al.High step-up Boost converter based on topology combination[J].Transactions of China Electrotechnical Society,2012,27(6): 96-102.

[11]Li W,He X.Review of nonisolated high-step-up DC-DC converters in photovoltaic grid-connected applications[J].IEEE Transactions on Industrial Electronics,2011,58(4): 1239-1250.

[12]Silva F S F,Freitas A A A,Daher S,et al.High gain DC-DC Boost converter with a coupling inductor[C].IEEE Power Electronics Conference,COBEP'09,Brazilian,2009: 486-492.

[13]Hsieh Y P,Chen J F,Liang T J,et al.Novel high step-up DC-DC converter with coupled-inductor and switched-capacitor techniques for a sustainable energy system[J].IEEE Transactions on Power Electronics,2011,26(12): 3481-3490.

[14]胡义华,陈昊,徐瑞东,等.一种高升压比直流变换器[J].电工技术学报,2012,27(9): 224-230.

Hu Yihua,Chen Hao,Xu Ruidong,et al.A type of high step-up DC-DC converter[J].Transactions of China Electrotechnical Society,2012,27(9): 224-230.

[15]Bin Gu,Dominic J,Jih-Sheng Lai,et al.High Boost ratio hybrid transformer DC-DC converter for photovoltaic module applications[C].IEEE Applied Power Electronics Conference and Exposition(APEC),Orlando,FL,USA,2012: 598-606.

[16]Zhao Q,Lee F C.High-efficiency,high step-up DC-DC converters[J].IEEE Transactions on Power Electronics,2003,18(1): 65-73.

[17]Zhao Y,Li W,Deng Y,et al.High step-up Boost converter with passive lossless clamp circuit for non-isolated high step-up applications[J].IET Power Electronics,2011,4(8): 851-859.

[18]Benavides N D,Chapman P L.Modeling the effect of voltage ripple on the power output of photovoltaic modules[J].IEEE Transactions on Industrial Electronics,2008,55(7): 2638-2643.

[19]Fontes G,Turpin C,Astier S,et al.Interactions between fuel cells and power converters: inf l uence of current harmonics on a fuel cell stack[J].IEEE Transactions on Power Electronics,2007,22(2): 670-678.

[20]Rosas J,Mancilla-David F,Mayo-Maldonado J,et al.A transformer-less high-gain Boost converter with input current ripple cancelation at a selecTableduty cycle[J].IEEE Transactions on Industrial Electronics,2013,60(10): 4492-4499.

[21]Do H L.Integrated ZVS DC-DC converter with continuous input current and high voltage gain[J].International Journal of Electronics,2011,98(9):1199-1214.

[22]Garinto D.A new zero-ripple Boost converter with separate inductors for power factor correction[C].IEEE Applied Power Electronics Conference and Exposition (APEC),Orlando,USA,2007: 1309-1313.