船体三维变形响应的数值预报

任慧龙，于鹏垚，李 辉，冯国庆

（哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

船体三维变形响应的数值预报

任慧龙，于鹏垚，李 辉，冯国庆

（哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001）

针对航行中舰船变形问题，采用三维水弹性理论实现了波浪中舰船的动态变形预报。通过拟合不同模态下船体有限元模型的节点位移，实现了将三维模态信息应用于广义流固耦合界面条件。建立了舰船在规则波中的广义水弹性运动方程，求解出各阶振动模态的主坐标。将各阶弹性模态主坐标与预报位置的角变形矩阵相乘，得到角变形响应。针对某实船，分别采用三维水弹性方法和三维刚体方法进行计算，通过对船体结构角变形响应的对比，验证了三维水弹性方法的正确性，同时也证明了该方法在计算效率上的优势。

舰船变形；流固耦合；三维水弹性方法；模态分析；变形响应；数值预报

随着船舶的大型化，船体在波浪中航行时，由周围波动压力作用引起的弹性变形愈发明显。对于某些特殊用途的船舶（如科考船、军舰等），较大的动态变形会影响设备的正常使用，进而影响其正常作业。因此，国内外相关学者提出一些方法对船舶营运时的波浪载荷诱导的动态变形响应进行预报。陈曙梅等［1⁃4］分2步进行载荷预报和结构响应计算，这些学者先将舰船看作三维刚体结构来计算不同工况下波浪载荷，再将载荷加载到三维有限元结构上来获取船体变形，这种方法在后续论述中简称为刚体方法。陈敏康等［5⁃6］等采用二维水弹性理论对船体的变形进行预报。

刚体方法是在准静态假定下进行计算，无法反映真实船体结构动力响应特性，而且在计算船体角变形幅频响应时，需要针对较多频率进行压力加载和静力分析，工作量较大。二维水弹性理论是将船体结构简化为一根变截面的船体梁，不能够考虑船宽方向上船体结构的变形。本文利用三维有限元模型的模态分析结果，采用的三维水弹性预报方法实现了船体三维变形响应的数值预报。

1 船体角变形矩阵的建立

对角变形响应而言，关心的是一个位置相对另一位置的角变形，如船体上某位置相对于罗经平台的变形。本文引入角变形矩阵X3n×m来表达不同模态下不同位置间的相对角变形振型。为了便于进行描述，引入如图1所示坐标系，其中原点位于重心在静水面上的投影，x轴有船舵指向船艏，y由右舷指向左舷，z轴数值向上。

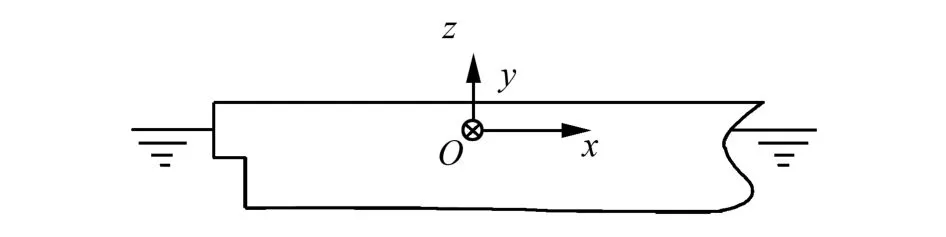
图1 坐标系Fig.1 Coordinate system

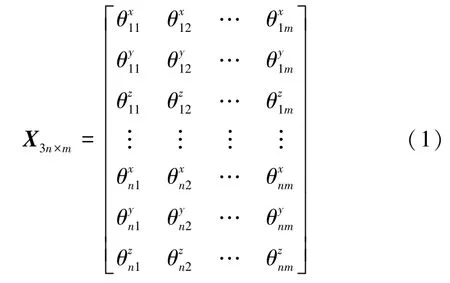
本文采用三维有限元方法对船体结构进行干模态分析，并以艉垂线与上甲板交点的线位移进行归一化，得到各阶弹性模态对应的振型，广义质量矩阵a，广义刚度矩阵c。

2 流固耦合界面条件的数值处理

基于势流理论求解舰船周围的流场时，需要求解流场的绕射势φd和辐射势φk。通常可采用源汇分布法［7⁃9］，结合自由面条件、远方条件和广义的流固耦合的界面条件［10］进行求取。

广义的流固耦合界面条件：

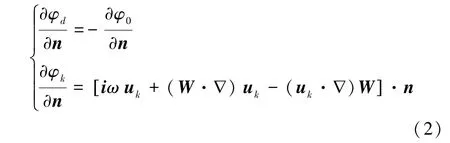
式中：φ0为已知的单位波幅入射势；ω为波浪自然频率；n为面元单位法向量；uk为第k模态下的面元中心点位移；W表示船体周围流场的定常速度，忽略定常速度势时，W＝-Ui，i为x坐标轴的单位方向向量，U为航速。

从式（2）可以看出，船体结构的振型信息是通过面元中心点的位移和该位移对x、y、z方向的偏导数体现在弹性结构的水动力求解中。因而，问题的关键就是如何通过三维模型在不同模态下的节点的位移信息来获得水动力求解中的面元中心点的位移和位移对x、y、z方向的偏导数。本文采用拟合位移形函数的方法来解决这一问题。

船体结构三维有限元模型的节点线位移矢量u＝（ux，uy，uz）包含3个方向的位移分量，本文以ux方向位移为例，推导出如何利用三维有限元模型外壳的振型信息确定对应模态下面元中心点的位移及其导数，其他两个方向位移的推导方法与其相同，不再赘述。

为便于后续描述，作如下定义：将面元中心点到面元节点的最远距离定义为面元控制域半径，以该半径作球的区域定义为面元控制域。则面元中心点的位移和位移的导数由面元控制域内节点的振型信息来确定。

对于空间运动的刚体，当给定刚体质心处的6自由度运动，便可以得到任意位置的位移：

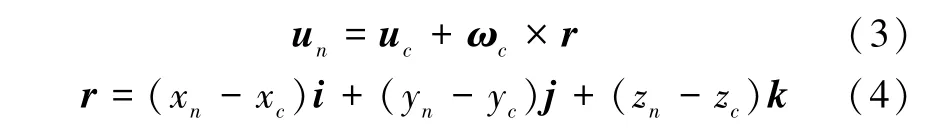
式中：un为待求任意一点的线位移；uc、ωc分别为质心处的线位移和角位移；r为待求位置与质心之间的向径；xn、yn、zn为待求位置的坐标；xc、yc、zc为质心坐标；i、j、k分别为x、y、z坐标轴的单位方向向量。

可见，任意节点线位移可由节点坐标与刚体质心处运动相乘的形式来表示。借鉴这种思路，当面元不与坐标轴垂直时，假定船体外壳上，面元对应区域内不同位置的x方向位移形函数具有如下形式：

式中：a0、a1、a2、a3为待定系数。

当面元与坐标轴垂直时，如与z轴垂直，控制域内的各个节点可能为同一个值，若同时为零，则a3为任意值，可导致后续求解方程组时系数矩阵奇异。故当面元与坐标轴垂直时，假定型函数的形式如下：

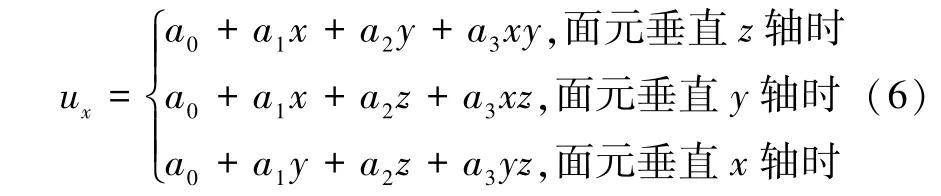
可以看出想要确定位移型函数，面元控制域内节点不得少于4，当少于4时可以适当增加控制域半径来增加节点。

若控制域内包含n个节点，可根据振型信息和位移型函数确定n个方程。方程的个数往往大于待定系数，即n＞4，此时可以基于最小二乘理论确定方程的系数，进而确定型函数，代入面元中心点坐标得到面元中心点位移。型函数分别对x、y、z方向求导，代入面元中心点坐标便得到面元中心点位移的导数。

对于与坐标轴垂直的面元，这里定性的确定该面元中心点位移对所垂直坐标轴方向的导数。如当面元垂直x轴时，该面元应位于结构的端部，通常对应于船体艏艉两端，该处对应的剖面内力为零，则各方向位移对x的导数应为零。同理对于垂直于y轴或z轴的面元，各方向位移对y轴或z轴的导数应为零。

3 船体角变形响应的求解

根据水弹性力学建立起适用于规则波激励下的广义线性水弹性运动方程［11］为

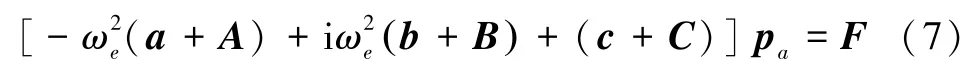
式中：a为船体广义质量矩阵，b为船体广义刚度矩阵，a和c可由前面的三维有限元结构模态分析获得；b为船体广义阻尼矩阵，可通过试验或经验公式获得；pa为主坐标幅值列向量；ωe为遭遇频率；A、B、C为广义水动力系数，具体含义分别为广义流体附加质量、广义流体附加阻尼和广义流体恢复力系数矩阵；F为广义波浪激励力。

对于广义水动力系数A、B、C和广义波浪激励力F，具体可依据下式求得：

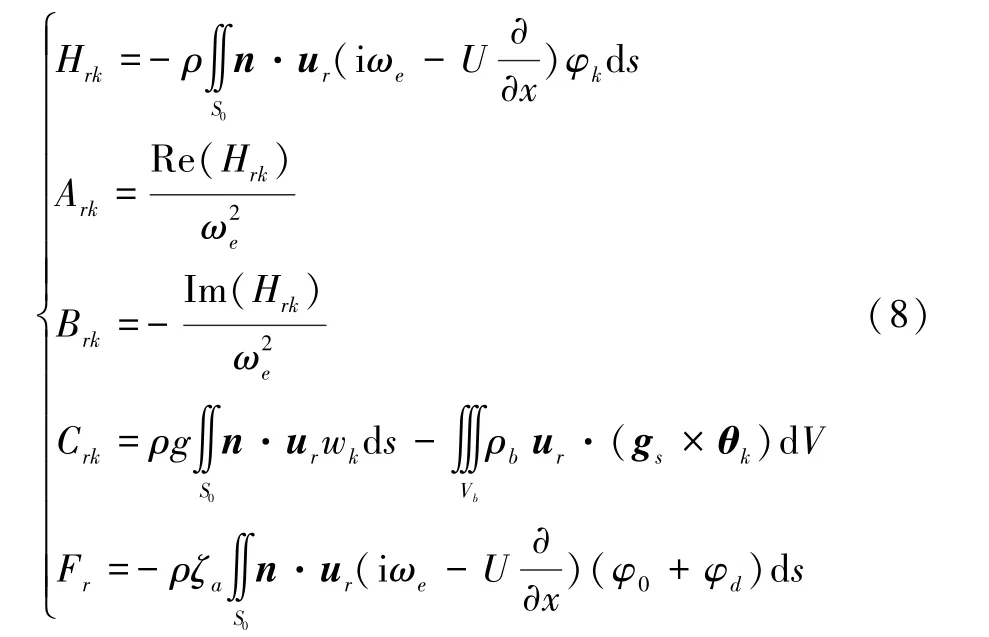
式中：ρ为流体的密度；ρb为船体结构材料的密度；ds为船体湿表面的面积微元；dV为船体结构的体积微元；n为面元中心点法向量；ur为第r阶模态下的面元中心点位移；φk为第k阶模态对应的辐射势；wk为第k模态下面元中心点的垂向位移；gs表示重力加速度矢量，gs＝（0，0，-g）；θk表示第k阶船体振型产生的结构转角变形，θk＝（∇×uk）／2；ζa为入射波波幅；φ0为已知的单位波幅入射势；φd为单位波幅绕射势；U为航速。

综上，在确定方程（7）的各项系数后，可求得在波浪激励下不同模态的主坐标响应。主坐标响应与角变形矩阵X3n×m相乘便可得到船体的任意位置间的角变形响应。

4 应用实例

利用提出的基于三维水弹性理论预报变形的方法，对某舰船在波浪作用下的角变形响应进行预报。首先，将三维水弹性得到的运动响应与传统的三维刚体载荷方法进行比较，然后再将刚体方法得到的波浪载荷加载到三维有限元模型上进行准静态分析，并提出取船体上任意位置间的相对角变形响应，最后将两种方法得到的角变形响应进行比较。

考虑到对于船体上任意位置间的相对角变形响应预报方法相同，本文仅以船体甲板上某一位置相对于船舯附近的罗经平台的变形为例进行角变形响应预报。为了便于设备的使用，预报点位置和罗经平台都在船体的强力构件附近，并采取了局部加强。

4.1 舰船主尺度数据及关注位置

选取某船舶进行船体三维变形响应的数值预报的相关研究，船舶的主尺度数据和关注位置坐标分别如表1、2所示。

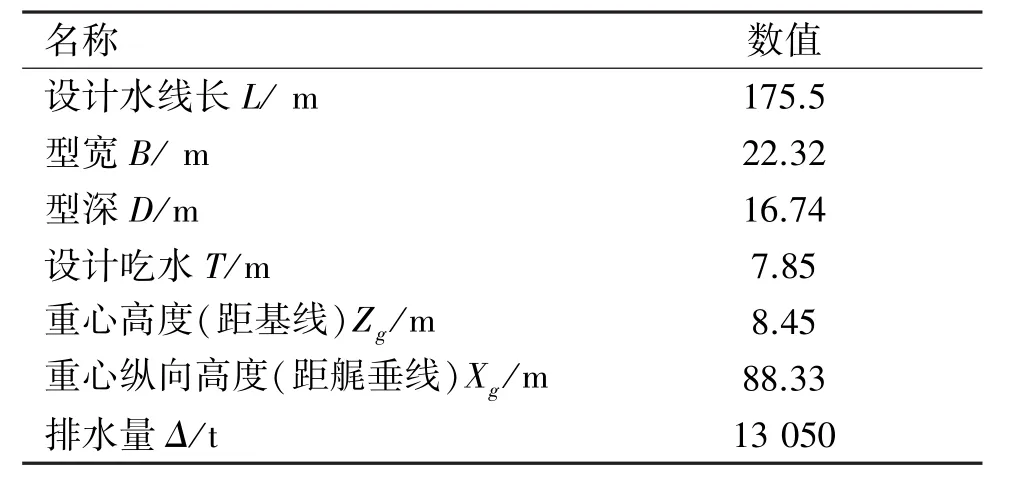
表1 舰船主尺度数据Table1 Principal parameters of the ship

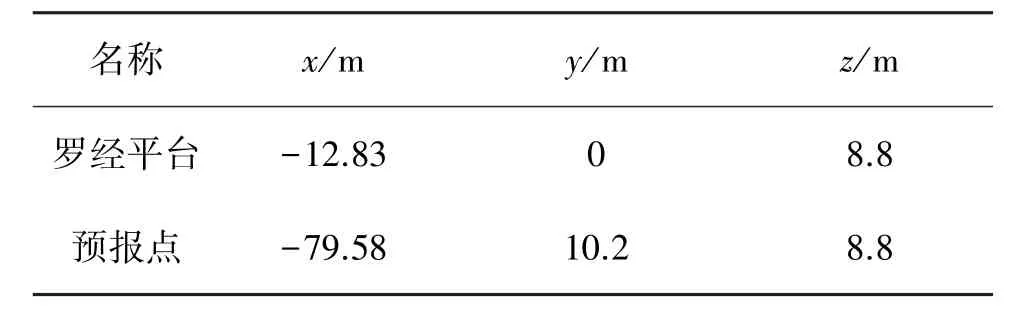
表2 关注位置坐标Table2 Coordinates of concerned positions

4.2 干模态分析

本文采用有限元软件MSC.nastran对船体整船结构干模态进行分析，考虑到关注的位置位于甲板上，在图2中列出弹性模态对应甲板位置的振型。表3列出各阶模态固有频率、广义质量和无因次阻尼系数。表4给出关注位置相对罗经平台的角变形矩阵。实际计算中，所选取的弹性模态的数目将在后续进行进一步的讨论。对于船体自身的结构阻尼，理论计算很难实现精确的确定，而且结构阻尼主要影响船体与波浪共振时的响应峰值，对低频波浪激励下的结构响应影响不大，因而本文计算中的阻尼系数主要参照相关文献［12］的经验公式进行确定。本文仅以前4阶弹性模态为例列出模态分析结果，对于更多的模态只需扩展相应的行或列。

图2 弹性模态甲板振型Fig.2 Deck shape of elastic principal mode

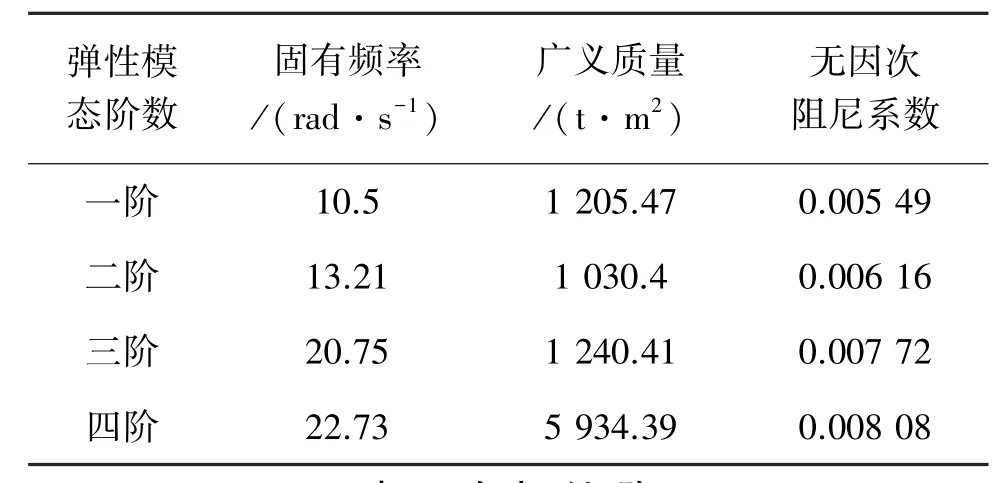
表3 船体干模态固有频率、广义质量和无因次阻尼系数Table3 Eigenfrequencies，generalized mass of flexible modes and nondimensional damping coefficients

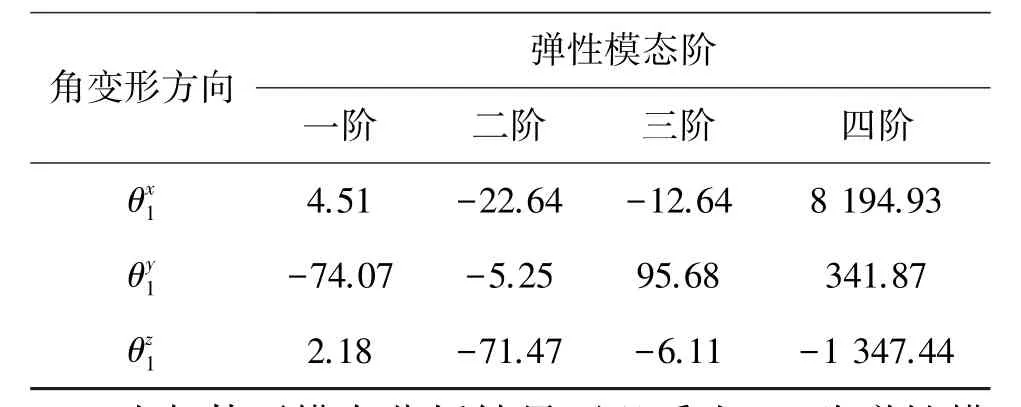
表4 角变形矩阵Table4 Angular deformation matrixmin

由船体干模态分析结果可以看出，一阶弹性模态振动形式以两节点的垂向振动为主。若采用二维的船体梁模型进行模态分析，对于对称船体，该模态下任意位置处绕x和z轴的角变形均为0，而由三维有限元方法得到相对角变形矩阵可以看出，在一阶弹性模态下，绕x和z轴的对应元素并不0，说明由于船体结构的局部特点影响，在以垂向振动为主模态下，对于绕x和z轴的角变形也有贡献。

4.3 弹性模态数目的选取

对于实际的船体结构，从理论上说，它具有无限种振动形式，然而在采用模态叠加方法计算某一种外力激励下的结构响应时，不可能考虑到结构所有模态，只能够尽可能的选取对结构响应贡献较大的模态用于计算。对于本文计算的船体结构，结构响应主要是由于波浪的激励引起的，而实际船体的固有频率通常大于波浪频率的分布范围，因而固有频率越低的模态越接近波浪频率，对结构响应贡献越大。本文为考察究竟多少个弹性模态能够充分反映船体关注位置的角变形响应，分别采用前4、8、12阶弹性模态用于水弹性计算。计算时，舰船航速为20 kn，浪向角为30°。图3为选取不同弹性模态数目进行计算时的角变形幅频响应曲线。

通过计算可以看出，选取4个弹性模态数目的计算与选取8和12个弹性模态的计算结果差别较大，选取8个和12个弹性模态的计算结果几乎相同，说明选取8个弹性模态已经能够充分反映出该海况下船体关注位置的角变形响应，其中第8阶弹性模态对应的干模态固有频率为34 rad／s，大于波浪能够激励的结构干模态频率范围。因而后续采用三维水弹性方法进行计算时均采用8个弹性模态。

图3 不同模态数目下角变形幅频响应曲线Fig.3 Angular deformation amplitude⁃frequency re⁃sponse curves of different mode numbers

4.4 变形响应的对比

在航速20 kn，浪向角30°时，分别采用三维水弹性方法和加载三维刚体方法的波浪载荷的方法预报船体的角变形的幅频响应，如图4。

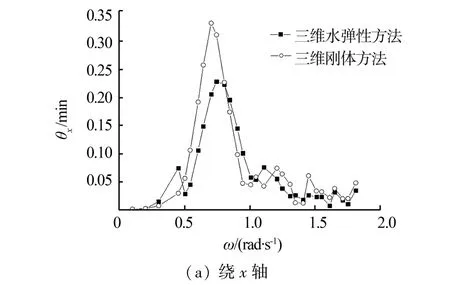
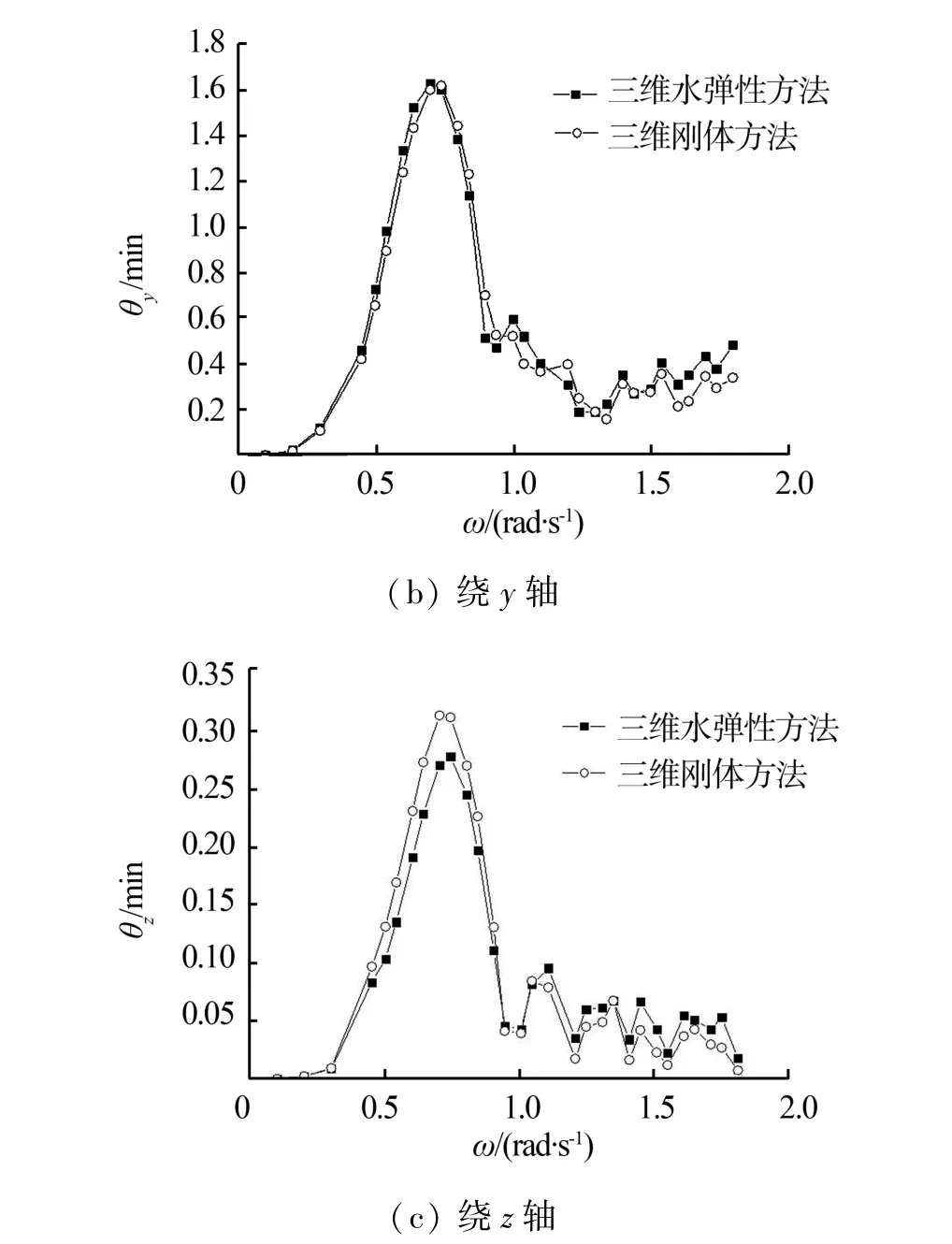
图4 2种方法的角变形幅频响应曲线Fig.4 Angular deformation amplitude⁃frequency re⁃sponse curves of the two methods

通过对比可以看出，2种计算结果的趋势基本一致，而且绕y轴的角变形明显大于绕x、z轴的角变形。对于绕x、z轴的角变形，刚体方法的计算结果大于水弹性方法，对于绕y轴的角变形，2种方法基本一致。分析如下：三维水弹性方法是一种考虑到流固耦合的动力分析方法，而刚体方法是在船体是刚体，结构响应是准静态的假定下进行的计算，因而2种方法的计算结果必然存在偏差。总体的看来，对于船体角变形比较大的方向（绕y轴角变形），2种方法预报结果几乎相同，一定程度上验证了水弹性方法正确性。

5 结论

对于预报舰船在波浪中角变形这一流固耦合问题，本文采用拟合位移形函数的处理方法，实现将三维有限元的模态分析结果应于与三维水弹性理论来预报结构的角变形响应。通过计算表明：

1）本文所选用的前8阶弹性模态已足够可以反映出关注位置处的角变形响应。

2）通过刚体方法和水弹性方法的变形响应对比，验证了采用拟合位移形函数的方法处理流固耦合界面条件的正确性。

3）通过水弹性方法，避免了将水动压力加载到有限元模型上，可以快速的获得舰船的变形幅频响应，方便了后续变形响应的长短期分析和可靠性分析。

［1］陈曙梅.航行状态下舰船结构总体变形分析［D］.哈尔滨：哈尔滨工程大学，2004：7⁃42.

CHEN Shumei.Deformation analysis of whole vessel in navi⁃gating state［D］.Harbin：Harbin Engineering University，2004：7⁃42.

［2］LIU Aili，MA Hongxu，Dai Hongde.Estimation method for ship deformation under wave Loads［C］／／International Con⁃ference on Mechanic Automation and Control Engineering.Wuhan，China，2010：93⁃96.

［3］MURAWSKI L.Shaft line alignment analysis taking ship construction flexibility and deformations into consideration［J］.Marine Structures，2005，18：62⁃84.

［4］YU Pengyao，FENG Guoqing，REN Huilong，et al.Deform⁃ation analysis and reliability assessment of ship hull in irreg⁃ular waves［C］／／Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering.Nantes，Frances，2013.

［5］陈敏康，邱强.随机波浪中船体变形转角的估算方法及应用［J］.船舶力学，2006，10（2）：87⁃95.

CHEN Minkang，QIU Qiang.Estimate method and its appli⁃cations for angular deflection of girder in random wave［J］.Journal of Ship Mechanics，2006，10（2）：87⁃95.

［6］TAYLOR R E.Reflections on the structural dynamics of floating beams and ship hulls in waves［J］.Journal of Engi⁃neering for the Maritime Environment，2009，223（3）：257⁃273.

［7］刘应中，缪国平.船舶在波浪中的运动理论［M］.上海：上海交通大学出版社，1987：56⁃80.

［8］戴遗山，段文洋.船舶在波浪中的势流理论［M］.北京：国防工业出版社，2007：63⁃84.

［9］李辉.船舶波浪载荷的三维水弹性分析方法研究［D］.哈尔滨：哈尔滨工程大学，2009：46⁃66.

［10］夏锦祝，吴有生.流固耦合问题的一个一般交界面条件［J］.舰船性能研究，1993（2）：15⁃22.

XIA Jinzhu，WU Yousheng.One common interface condi⁃tion of fluid solid interaction problem［J］.Ship Perform⁃ance Research，1993（2）：15⁃22.

［11］李辉，任慧龙，刘日明，等.FPSO运动与波浪载荷三维水弹性分析方法研究［J］.哈尔滨工程大学报，2008，29（8）：789⁃793.

LI Hui，REN Huilong，LIU Riming，et al.3⁃D hydroelas⁃tic method for analysis of motion and wave loads of an FP⁃SO ship［J］.Journal of Harbin Engineering University，2008，29（8）：789⁃793.

［12］董艳秋.船舶波浪外荷和水弹性［M］.天津：天津大学出版社，1991：104⁃141.

Numerical prediction of three dimensional deformation response of the ship hull

REN Huilong，YU Pengyao，LI Hui，FENG Guoqing
（College of Shipbuilding Engineering，Harbin Engineering University，Harbin 150001，China）

Aiming at the deformation problem of the navigating ship，the three dimensional（3D）hydroelastic meth⁃od is adopted to predict the dynamic deformation of ships in waves.Through fitting the nodes displacement of differ⁃ent vibration modes，the modal information of the 3D finite model is applied to the generalized interface boundary condition of fluid⁃structure interactions.Then，generalized hydroelastic equations of ship motion are established and the principal coordinates of different order vibration modes are solved.Furthermore，the angular deformation re⁃sponse could be achieved through multiplying the angular deformation matrix and the principal coordinates of differ⁃ent order elastic vibration modes.Take a real ship as an example，the 3D hydroelastic method and the 3D rigid method are applied to calculate the deformation response of the ship，respectively.Through comparing the results from the two methods，the correctness and high efficiency of the 3D hydroelastic method are proved.

ship deformation；fluid and structural interactions；3D hydroelastic method；modal analysis；fluid⁃structure interactions；angular deformation matrix；deformation response；numerical prediction

10.3969／j.issn.1006⁃7043.201311053

U661.3

A

1006⁃7043（2015）01⁃0134⁃05

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006⁃7043.201311053.html

2013⁃11⁃15.网络出版时间：2014⁃11⁃07.

国家自然科学基金资助项目（51079034）.

任慧龙（1965⁃），男，教授，博士生导师.

任慧龙，E⁃mail：renhuilong＠263.net.