交通小区的两维图论聚类

冯树民，马栋才

（哈尔滨工业大学交通科学与工程学院，150090哈尔滨）

交通小区的两维图论聚类

冯树民，马栋才

（哈尔滨工业大学交通科学与工程学院，150090哈尔滨）

为使得交通小区合并生成交通中区的过程更加合理，同时考虑交通小区之间的相似性和位置关系，将两维图论聚类法应用于交通小区的合并.给定交通小区相邻满足的条件，并用邻接矩阵表示交通小区之间的位置关系，构造无向加权图并求解最小支撑树，根据最小支撑树选取阈值进行交通小区合并，最后用F检验法确定理论上的最优合并结果作为小区合并结果选取的参考.实例分析结果表明：聚类数随阈值的增大而减少，而且合并过程中只有相似且相邻的交通小区被合并，并采用F检验法确定了唯一的最优合并参考方案，划分结果合理可行.

交通工程；交通小区合并；两维图论聚类法；交通小区；位置关系

在城市交通规划中需要将规划区域划分为若干个交通区，根据不同的研究层次交通区可分为交通小区、交通中区和交通大区，其中交通小区是规划研究中的最小区域单元.交通小区划分应遵循划分原则并满足交通需求预测的精度，同时应尽量减少交通调查与数据分析的工作量.而交通小区合并是交通小区划分的逆向过程，合并可生成用于交通需求预测等实际研究问题的交通中区［1］.由此可见，交通小区的合并有着重要的实际意义，与交通小区的划分同等重要.

对于交通小区的划分，文献［2］应用空间句法理论中的深度值进行交通小区划分，得到了满意的结果；文献［3］在分析空间聚类分析算法的基础上，建模并设计了交通小区划分的流程和算法，实现了小区的自动划分；文献［4］分析了出行距离的概率密度和概率分布，提出了基于出行距离的交通小区划分方法；文献［5］克服了传统静态交通小区划分的缺点，提出了基于博弈论的动态划分法；文献［6］引入图的矩阵，提出了基于图的谱理论的划分法；文献［7］利用移动计费数据进行交通小区划分，该方法具有覆盖率高、成本低的优点.对于交通小区的合并，一般的做法是有经验的规划人员结合研究区域的实际情况，在交通规划软件TransCAD中将一些性质相似的小区人为地合并.此外，由于交通小区的合并类似于聚类过程，也可通过聚类技术实现交通小区合并，文献［8-11］应用模糊聚类法，根据反映交通小区特性的土地利用指标或经济指标，将相似的小区合并.

综上，有关交通小区合并的研究相对较少且方法单一.其中人为地合并交通小区的做法主观因素强、没有统一标准，不同人的划分结果也不尽相同；而基于模糊聚类分析的交通小区合并虽然克服了人为合并的缺点，使得合并过程更加科学，但模糊聚类法只能根据交通小区之间的相似性聚类（合并），而无法识别交通小区之间的位置关系（空间邻接性），其应用也存在着一定的不足：在聚类的过程中会将一些不相邻的交通小区合并，这样的结果在实际应用中显然不合理，如文献［4］中在结果选取时还得人为地将不相邻的小区分开.因此，同时考虑位置关系与相似性的交通小区合并值得重点研究.

1 交通小区位置关系分析

在交通小区合并生成交通中区的过程中不仅要考虑小区之间的相似性，还要考虑其位置关系.因此，需要对交通小区之间的位置关系进行必要的分析.交通小区之间的位置关系只有相邻与不相邻两种.为明确交通小区之间的位置关系，给定交通小区相邻必须满足以下条件.

1）在初始交通小区划分图上，交通小区i与j在空间位置上相邻.

2）交通小区i与j之间的分界线不是河川、铁路等天然屏障，而是人为划定的交通小区分界线.如果小区之间的分界线是天然屏障，即使空间位置上相邻也不算相邻.

3）只有同时满足以上两个条件的两个交通小区才算相邻.

为方便编程求解，根据交通小区划分方案及相邻条件，用对称的邻接矩阵L= lij[ ]n×n表示小区i与j之间的位置关系，L中的邻接元素为

2 两维图论聚类法

2.1 两维图论聚类法的原理及优势

图论聚类法是由 Zahn提出的，又称为最大（小）支撑树聚类算法.一般的图论聚类算法中，无向加权图中对象 i与 j之间的连接边 eij的权值w（eij）定义为对象之间的相似程度，而相似程度可用欧氏距离或相似系数描述.欧氏距离越小（相似系数越大）表示对象之间相似程度越高，反之则越不相似.如果采用欧氏距离作为无向图连接边的权值，则构造无向加权图并求解最小支撑树，移去最小支撑树中大于阈值的边形成森林，森林中连通的对象合并为一类.如果采用相似系数作为无向图连接边的权值，则构造无向加权图并求解最大支撑树，移去最大支撑树中小于阈值的边形成森林，森林中连通的对象合并为一类［12］.

在传统图论聚类算法的基础上，同时考虑聚类对象之间的相似性与空间邻接性形成两维图论聚类算法.与一般的图论聚类算法相比，两维图论聚类算法的主要区别在于无向加权图的构造：只有相邻的对象才连接，而一般图论聚类法不考虑聚类对象的空间邻接性.此时，基于聚类对象空间邻接性及其相似性的无向加权图也是一个加权连通图［13］.因此，两维图论聚类法在涉及位置关系的聚类问题中明显优于一般聚类方法.如根据图1中4个交通小区之间的位置关系，可构造如图2所示的无向加权图.

图1 交通小区划分图

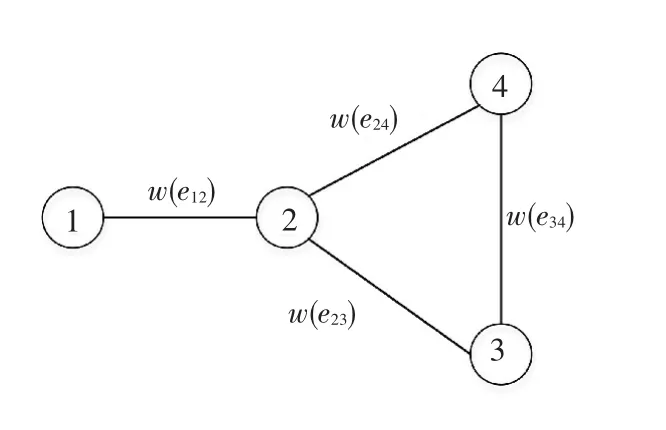
图2 小区加权无向图

2.2 聚类指标及处理

影响交通小区划分的重要因素是用地性质的差异，例如居民区早晚高峰由于工作、上学等出行活动将会有较大的出行量，商业区具有很强的交通吸引力［14］，居民区与商业区呈现出的交通特性取决于用地性质.因此，交通小区合并时以用地性质作为关键指标，保证被合并的交通小区在用地性质方面有较强的相似性，即交通特点相似.用地性质可分为居住用地、道路交通用地、工业用地、生态用地、仓储用地、商业服务设施用地、公共管理与服务用地、公用设施用地；其次，由于交通小区划分的重要目的就是将交通的产生、吸引与一定区域的社会经济指标联系起来分析其相关规律［8］，因此选取交通小区的经济指标GDP反映其经济情况；最后考虑各个交通小区的人口数量.于是，各个交通小区的用地性质、经济指标、人口数量组成了交通小区的聚类指标体系.

n个交通小区组成样本集合X= {x1，x2…，xn}，如果交通小区i有m个反映其特性的指标，则表示为 xi= {xi1，xi2，…，xim，}，i=1，2，…，n，n个交通小区构成原始数据矩阵 xij[ ]n×m.由于不同特性具有不同的量纲，需要对原始数据进行标准化处理来消除量纲的影响，一般采用标准差标准化.为了将标准化后的数据压缩在［0，1］，再进行极值标准化，即

2.3 连接边的权值

交通小区合并过程中需要构造基于位置关系的无向加权图，连接边的权值用相似系数或欧氏距离表示.小区i与j之间的欧氏距离和相似系数分别为

其中，欧氏距离一般适用于二维或三维空间的对象间相似性的度量［15］，欧氏距离和相似系数之间还可以相互转换［16］，即

2.4 合并结果的确定

应用两维图论聚类法选择不同阈值进行交通小区合并，最终采用F检验法［16］确定最佳阈值.由原始数据矩阵可得所有聚类对象的中心为

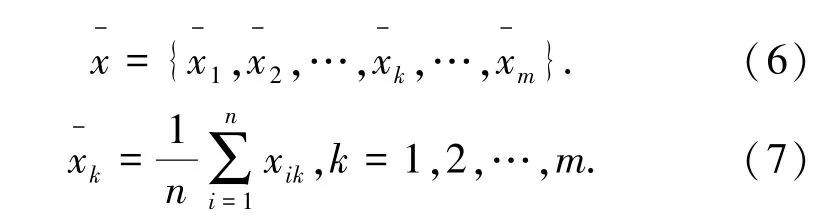
假设聚类数为s，第j类含有nj个对象，则第j类样本的聚类中心为

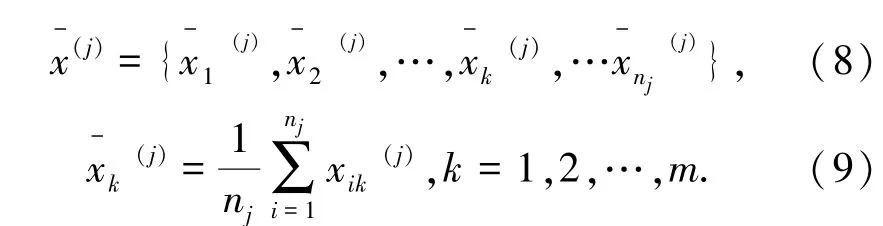
于是可构造F统计量为

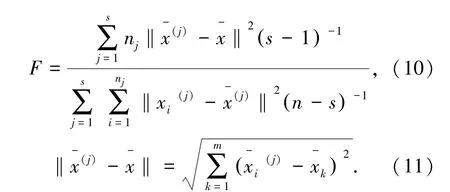
F统计量服从自由度为s-1、n-s的F分布，式（10）中分子表示不同类之间的距离，分母表示同一类样本之间的距离.在一定的显著水平α下，通过显著性检验且F值越大，说明不同类对象之间的差异越大、同类对象之间的差异越小，即聚类效果越好.

交通小区合并生成中区的过程中，在最小（最大）支撑树的基础上选取阈值进行合并，计算合理分类结果对应的F值并进行显著性检验，然后结合规划层次的需求选取F值最大的合并结果.

2.5 交通小区合并的流程

基于以上分析，给出应用两维图论聚类法进行交通小区合并的流程，如图3所示.

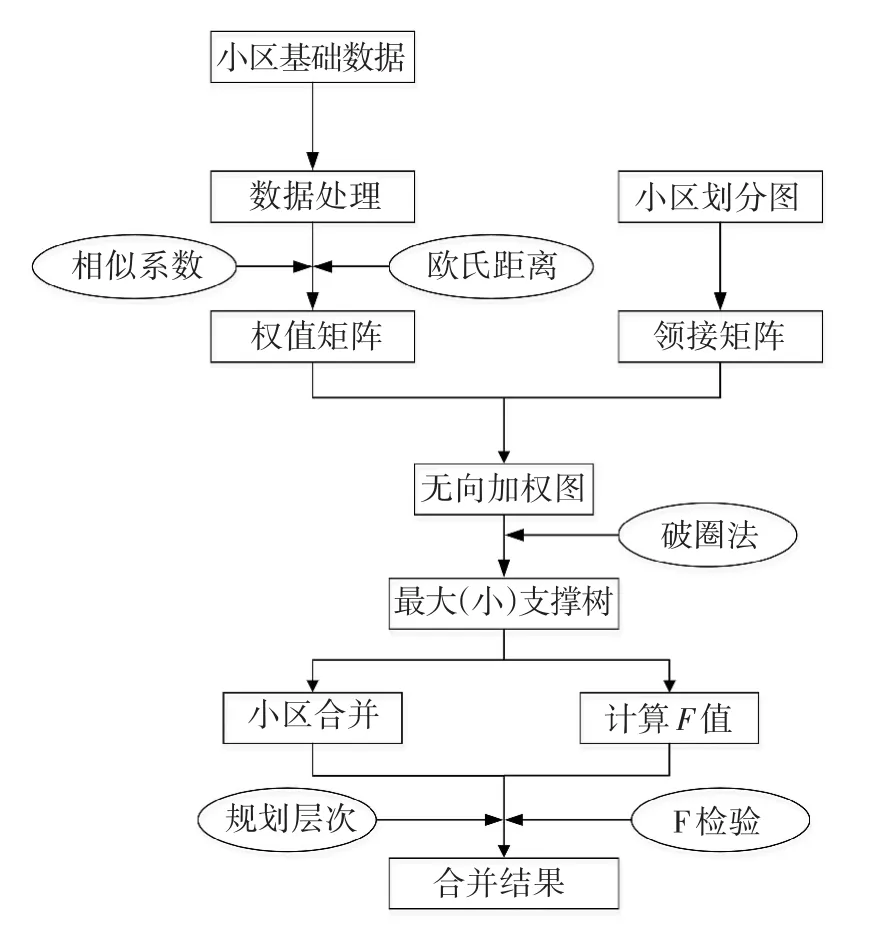
图3 交通小区合并流程

其中，在根据交通小区划分图求邻接矩阵时，为避免面积较大的交通小区直接合并形成过大的交通中区，可结合交通小区划分情况，将面积较大的小区之间的邻接元素lij赋值为0，使得面积较小，相邻且相似的交通小区先被合并，从而得到大小适宜的交通中区.

3 实例分析

以东莞市南城区为例进行实例分析，介绍两维图论法在交通小区合并中的具体应用.初始交通小区划分图如图4所示.

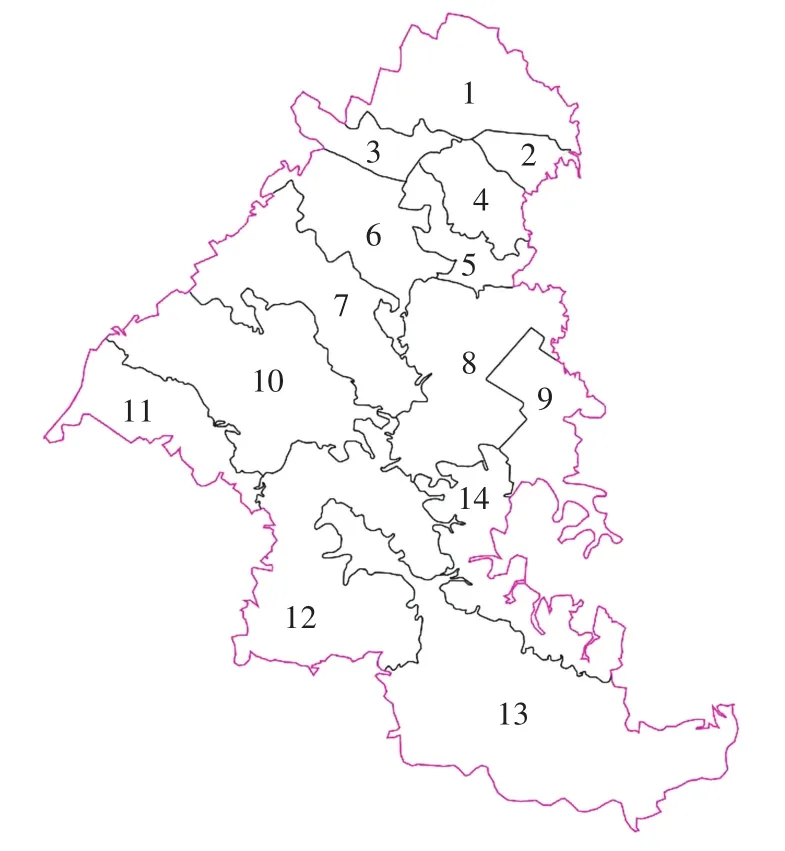
图4 初始交通小区划分图

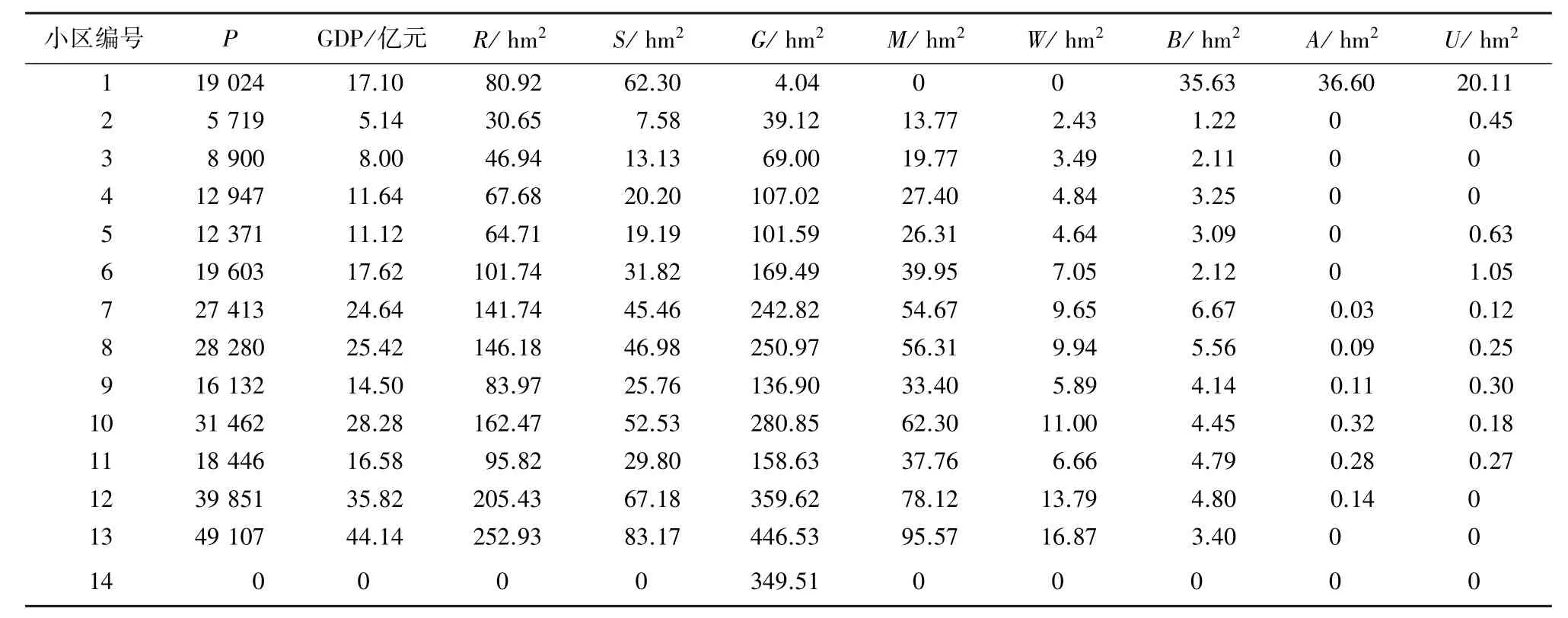
图4中的数字代表14个分区，各个小区的聚类指标如表1所示.P为小区人口数；GDP为小区的生产总值，亿元；R为居住用地面积，hm2；S为道路交通用地面积，hm2；G为生态用地面积，hm2；M为工业用地面积，hm2；W为物流仓储用地面积，hm2；B为商业服务设施用地面积，hm2；A为公共管理与公共服务用地面积，hm2；U为公用设施用地面积，hm2.数据来源于东莞市轨道交通相关项目.

从表1及图4中可以看出，交通小区7、8、10、12、13的面积明显大于其他交通小区，为避免这5个小区两两直接合并形成过大的交通中区，可令这5个小区两两之间的邻接元素为0，然后根据式（1）及图4得邻接矩阵L.表1中各项指标单位不统一，首先进行标准差标准化，然后采用式（2）将数据压缩到［0，1］.由于聚类指标数大于3，因此选择用相似系数式（4）描述小区之间的相似性.为了便于利用MATLAB中求解最小支撑树的graphminspantree函数编程实现交通小区的合并，采用式（5）将相似系数转化为距离，得到权值矩阵W（对称矩阵）如下，最小支撑树如图5所示.

?

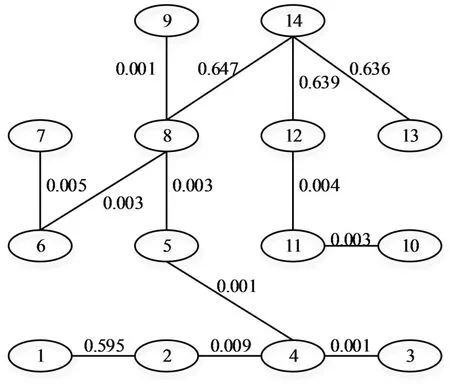
图5 最小支撑树

MATLAB编程获得最小支撑树中所有互不相同的权值，将这些权值作为阈值并对其排序如下：0.001、0.003、0.004、0.005、0.009、0.595、0.636、0.639、0.647.当选择阈值为0.001时，移去最小支撑树（见图5）中权值大于0.001的边形成森林，如图6所示.

由图6可知，交通小区3、4、5连通，交通小区8、9连通，根据两维图论聚类原理，交通小区3、4、5被合并，交通小区8、9被合并，分别形成集合｛3，4，5｝、｛8，9｝，每个集合代表一个新区.选择其余的阈值进行交通小区合并，结果如表2所示.

图6 森林

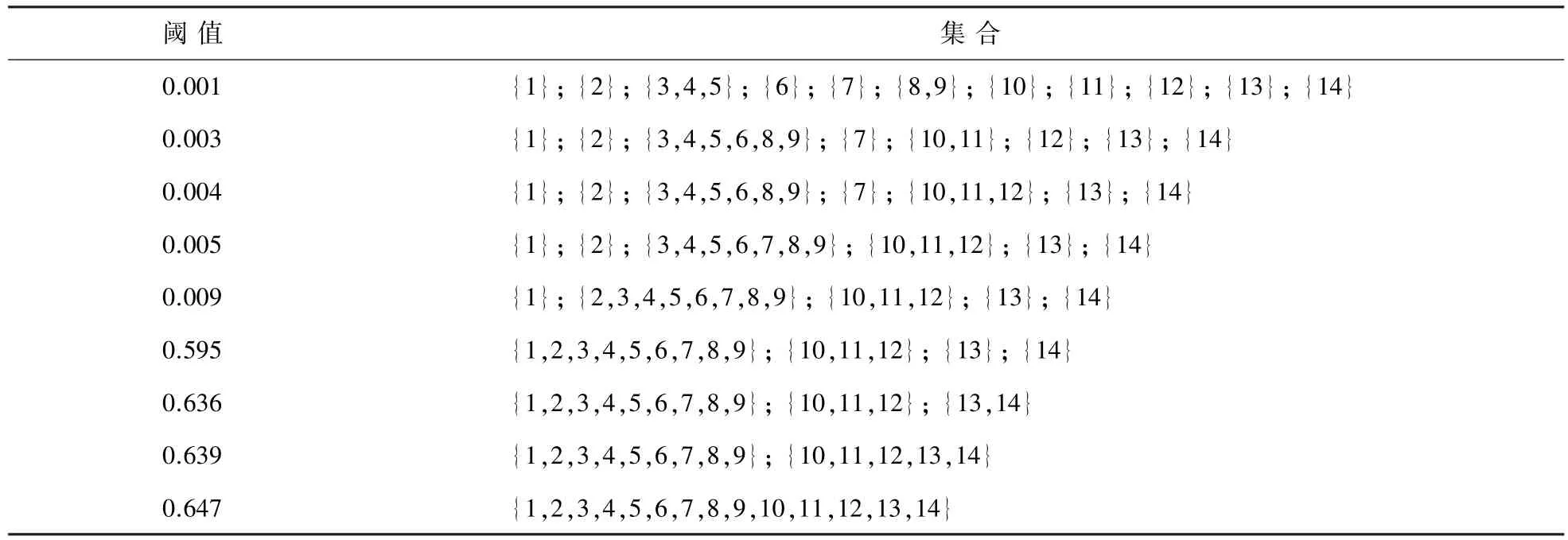
表2 不同阈值下的合并结果

由于阈值为距离，表示的是交通小区之间的相似程度，被合并的小区之间的相似程度随阈值的增大而减小.表2为F检验结果，可见：随着阈值的增大，聚类数减少，被合并的小区增加；当阈值为0.647时，所有的小区被合并为一个；而且所有合并结果中均没有出现不相邻的交通小区合并的情况.当阈值≥0.005时，合并形成的小区过大，因而在最佳合并结果确定时不予考虑.为确定最佳阈值，采用式（10）编程计算阈值对应的F值，并给出α=0.05水平下的临界值进行显著性检验，结果见表3.

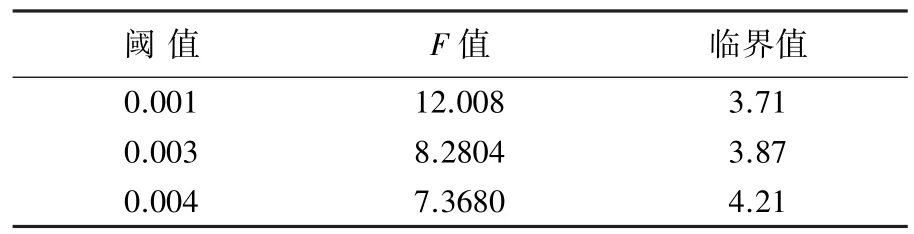
表3 F检验结果

从表3中可以看出，F值均大于临界值且0.001对应的F值最大，因此最佳阈值为0.001，原来的14个交通小区合并为11个.此外，从权值矩阵W中可以看出，小区12与13（7与8；10与12）相邻且距离为0，表明这两个小区极其相似，可看作一个小区.但这两个小区的面积均明显大于其余小区，合并后再与其余小区合并将使得合并生成的中区面积过大.本案例中通过邻接矩阵，有效限制了面积较大的交通小区直接合并，避免形成过大的交通中区.

本案例如应用文献［1］采用的模糊聚类分析进行交通小区合并，结果如表4所示.

由表4可知，当阈值为0.999 575时，交通小区4、7、8、9、10、11、12、13被合并，而在初始交通小区划分图中（图4）交通小区4与其他几个小区均不相邻.当阈值分别为0.999 628、0.999 651、0.999 665、0.999 699、0.999 887、0.999 936时也出现类似的情况，这样的合并结果显然不合理，原因在于模糊聚类法没有考虑交通小区之间的邻接关系.由于两维图论聚类法是基于交通小区的空间邻接性与相似性进行合并，表2所示的合并结果中均不会出现不合理的合并结果.

表4 模糊聚类方法合并结果

4 结 论

1）在交通小区合并生成交通中区的过程中应用两维图论聚类法，能够有效克服现有方法无法识别交通小区位置关系的缺点，避免将不相邻的小区合并，使得交通小区合并生成交通中区的过程更加科学，合并结果合理可行，为交通小区合并产生交通中区提供了理论依据.

2）通过计算不同分类对应的F值并进行F检验，可确定最大F值对应的最优合并结果，为最终小区合并结果的选取提供参考，克服人为选择主观因素强的缺点，将定量分析与定性分析的结果相结合，使得交通小区合并生成的交通中区更符合实际情况.

3）两维图论聚类法不仅适用于交通小区合并生成交通中区，还适用于交通中区合并生成交通大区的工作.

［1］宋亮.交通小区的理论分析和划分方法研究［D］.西安：长安大学，2011.

［2］ XUE Y，DUAN Z Y.An accessibility oriented traffic analysis zone division method［C］／／2010 2nd International Asia Conference on Informatics in Control，Automation and Robotics.Wuhan：IEEE Computer Society，2010：516-519.

［3］李晓丹，杨晓光，陈华杰.城市道路网络交通小区划分方法研究［J］.计算机工程与应用，2009，45（5）：19-22.

［4］WU S M，CHENG G Z，PEI Y L.Model of traffic zone division based on trip distance［J］.Applied Mechanics and Materials，2013，409-410：1184-1187.

［5］LIU H Q，YANG L C，ZHANG Y，et al.A dynamic traffic zone division scheme based on game theory［J］.Journal of Information and Computational Science，2013，10（10）：2961-2969.

［6］WU S M，PEI Y L，CHENG G Z.Method of traffic zone division based on spectral graph theory［J］.Computer Modelling and New Technologies，2014，18（2）：186-191.

［7］XING X X，HUANG H W，SONG G J，et al.Traffic zone division using mobile billing data［C］／／2014 11th International Conference on Fuzzy Systems and Knowledge Discovery.Xiamen：Institute of Electrical and Electronics Engineers Inc，2014：692-697.

［8］于慧杰.交通小区在交通规划中若干技术问题的研究［D］.西安：西安电子科技大学，2008.

［9］杨波，刘海洲.基于聚类分析的交通小区划分方法的改进［J］.交通与运输：学术版，2007（1）：5-7.

［10］桂小玲，靳文舟，胡郁葱.模糊聚类分析方法及其在交通规划中的应用［J］.交通与计算机，2005，23（2）：80-83.

［11］刘乙霏.基于模糊聚类的交通小区划分方法研究［J］.物流科技，2011（9）：25-28.

［12］高兴波.模糊聚类分析及其应用［M］.西安：西安电子科技大学出版社，2004，37-48.

［13］谷晓岩，李凤英，张燕.两维图论聚类法在农业区划中的应用：以山东省十七地市为例［J］.安徽农学通报：上半月刊，2009，15（3）：62-64.

［14］伍拾煤.密集城镇群多层级轨道交通客流预测模型研究［D］.哈尔滨：哈尔滨工业大学，2014.

［15］唐东明.聚类分析及其应用研究［D］.成都：电子科技大学，2010.

［16］王晟.模糊聚类算法的研究与实现［D］.南京：南京理工大学，2006.

（编辑 魏希柱）

Two-dimensional graphic theory on clustering method of small traffic zones

FENG Shumin，MA Dongcai

（School of Transportation Science and Engineering，Harbin Institute of Technology，150090 Harbin，China）

In order to make the process of generating small traffic zones into middle traffic zones more reasonable and taking the similarity and the positional relation of small traffic zones into consideration，two-dimensional graphic theory-clustering method on the mergence of small traffic zone is applied.Given conditions that satisfied the adjacent small traffic zones，the positional relation of small traffic zones by the adjacent matrix is re-formulated.After the undirected weighted graph construction，the minimum spanning tree（MST）was solved.Choose the threshold according to the MST for the small traffic zones mergence.Finally the F-test is used to determine the optimal mergence in theory which is the reference of the selection of the small traffic zone mergence.The result of example analysis shows that the clustering number reduces along with the increase of the threshold value，and only the similar and adjacent small traffic zones can be merged during the mergence.In addition，the F-test is adopted to determine the exclusive optimal scheme of mergence for reference，which proved that the division result was feasible.

traffic engineering；small traffic zone mergence；two-dimensional graphic theory on clustering method；small traffic zone；positional relationship

U491

A

0367-6234（2015）09-0057-06

10.11918／j.issn.0367-6234.2015.09.011

2015-06-09.

国家高技术研究发展计划（2014AA110304）.

冯树民（1973—），男，教授，博士生导师.

马栋才，madongcai1990＠126.com.