钢管超快冷过程数学模型的研究与开发

冯莹莹，骆宗安，王立鹏，回楠木

（1.东北大学轧制技术及连轧自动化国家重点实验室，辽宁沈阳110819；2.东北大学信息科学与工程学院，辽宁沈阳110819）

钢管超快冷过程数学模型的研究与开发

冯莹莹1，骆宗安1，王立鹏1，回楠木2

（1.东北大学轧制技术及连轧自动化国家重点实验室，辽宁沈阳110819；2.东北大学信息科学与工程学院，辽宁沈阳110819）

为了提高钢管超快冷过程的温度控制精度、冷却均匀性以及组织性能控制的精准度，分析了钢管超快冷过程的换热机理，确定射流冲击为钢管超快冷过程的主要换热方式。利用反传热法对钢管表面换热系数进行测定；利用导热方程，建立钢管超快冷过程射流冲击换热数学模型，采用第三类边界条件和有限差分法求解该数学模型。应用此数据模型可以计算特定温度范围内的平均冷却速度和所用时间，也可以计算一定时间范围内的温降和平均冷却速度。经现场测试，由该数学模型计算得到的温降曲线与实际温降曲线基本相同，模型计算精度很高，具有可应用性和执行性。

钢管；超快冷；射流冲击换热；数学模型

以超快冷为核心的新一代TMCP技术在热轧板材、型材、棒材方面的生产应用已十分广泛［1⁃8］，但在钢管领域，其工业推广目前尚处起步阶段。区别于常规的“内喷外淋式”、“环形喷淋式”和“浸入式”等钢管冷却形式［9⁃12］，东北大学轧制技术及连轧自动化国家重点实验室自主研发的三层储水式环形斜缝喷嘴［13］使水流以一定的角度沿钢管运行方向将一定压力的水喷射到钢管表面，将钢管表面残存水与钢管之间形成的蒸气膜吹扫掉，从而达到钢管与冷却水之间的完全接触，实现核沸腾。这不仅提高了钢管和冷却水之间的热交换，而且可达极限冷却的冷却速率和极高的冷却均匀性，大大抑制了钢管由于冷却不均匀引起的弯曲变形。目前，该项技术已经在国内某钢厂得以应用。

淬火过程的数学模型是制约淬火过程自动控制的关键因素。为了提高超快冷过程的温度控制、冷却均匀性控制以及组织性能控制的精准度，研究与开发钢管超快冷过程的相关数学模型并予以应用是十分必要的。

1 钢管超快冷过程数学模型的建立

1.1 超快冷过程钢管传热状况分析

图1为钢管超快冷设备喷水示意图，冲击射流以螺旋形打到钢管的表面。

图1 超快冷设备喷水示意图Fig.1 Quenching Schematic diagram of ultra⁃fast cool⁃ing equipment

在钢管超快冷的过程中，钢管的外表面直接受超快冷设备的射流冲击，产生强烈的对流换热；在2组喷嘴之间，由于没有冲击射流，钢管部分短暂裸露于空气中，与空气产生对流换热，并且向外辐射热量。钢管的内表面由于没有冷却水进入，只存在与管内空气的自然对流换热和热辐射，但是由于管内空间较小，且只在钢管的两端有开口，相对封闭，因此管内空气对流换热所传递的热量近似等于管口处管内空气与管外空气的热量交换。同样的道理，钢管内表面的热辐射只有通过钢管两端的开口辐射到钢管外边，带走热量。其余的绝大部分热辐射只在钢管内表面不同部分之间产生热量交换，由于钢管内表面上并不存在温度梯度，所以并不产生热量的传递。而相对于射流冲击引起的强烈的对流换热，其他方式传递的热量均很少，所以可以忽略钢管外表面两组喷嘴之间与空气的对流传热和热辐射，以及钢管内表面的传热。

1.2 基于反传热法的综合换热系数测定

由于在冷却过程中，表面换热系数影响因素较多且各因素的影响权重很难确定，测定具体工艺条件下的表面换热系数比较困难。本文采用测温较容易、计算精度较高的反传热法来求解综合换热系数。求解过程为：在某一工况条件下，首先设定综合换热系数初始值，确定钢管表面初始换热条件；再利用导热差分方程求解指定时间段后的钢管温度分布，并计算出钢管终冷表面温度；最后通过比较温度计算值与测量值，不断修正换热系数设定值，直至温度计算值逼近测量值。此时所得换热系数即为该冷却段的综合换热系数［14］。计算过程中，导热方程采用可取得稳定数值解的Crank⁃Nicolson差分方法求解。

1.3 建立冲击射流的换热数学模型

建立冲击射流的换热数学模型就是得到任意超快速冷却条件下钢管温度场分布的计算方法。物体内温度场分布随时间和空间的变化要用导热微分方程来描述。导热微分方程的一般形式如下：

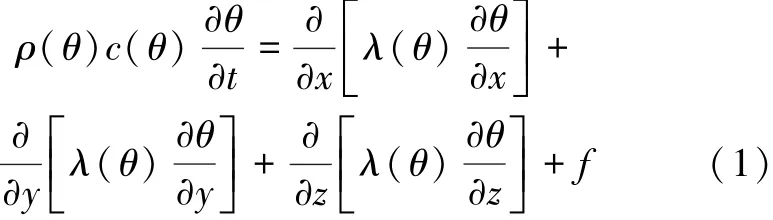
上述方程为三维条件下的导热微分方程，适用于非对称复杂条件下的温度场分布计算。由于冲击射流存在沿钢管圆周方向的速度，使射流在钢管表面的分布更加均匀，减小了重力对射流分布的影响，加之钢管自身的旋转，所以可近似将螺旋形冲击射流的分布看作沿钢管轴向对称分布。于是将钢管的超快速冷却看作是无限大平板的换热问题，因此将钢管的冷却问题简化为一维非稳态导热问题。直角坐标系下钢管的导热微分方程为

式中：θ为温度；t为时间；x为钢管厚度方向坐标，钢管内表面为原点；ρ（θ）为钢管密度；c（θ）为钢管的比热容；λ（θ）为钢管的导热系数；f为单位时间内单位体积内热源的生成热。

在钢管的冷却过程中，导热系数随温度的变化不大，所以可将导热系数看做常数，而比热容在钢管相变的过程中变化剧烈，不能忽略。但是在相变温度以外，数值基本相同，为简化计算，采取分段计算的方法。在相变温度范围和非相变温度范围，采用不同的比热容数值进行计算，在每一段内比热容值为常数，这样就使得结果准确且计算过程简化。此外在相变过程中会有相变潜热生成，考虑到超快冷时热量传递很快，钢管的相变潜热对冷却速度影响较小，可以忽略不计。所以在计算过程中ρ、c均为常数，f为0。于是导热微分方程的最终形式如下：

超快冷过程的导热问题采用第三类边界条件，即钢管与冲击射流的对流换热系数α和冲击射流的温度θf已知，且θf为常数。根据傅里叶定律，边界条件可以表示为

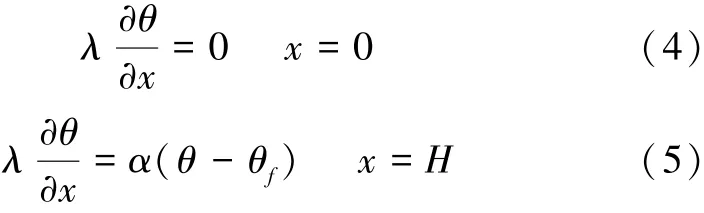
式中：H为钢管的厚度。

上述导热微分方程为二阶偏微分方程，采用有限差分法求解上述偏微分方程。将导热微分方程化成古典显示差分格式，过程如下：

一阶导数向前差分：

上述差分方程稳定性的条件为

将以上计算过程用C语言编程，确定相关参数，可以得到一系列温度-时间相对应的数据，利用此数据可以计算特定温度范围内的平均冷却速度和所用时间，也可以计算一定时间范围内的温降和平均冷却速度。

2 钢管超快冷过程温降的计算

2.1 参数确定

以超快冷设备的冷却能力为基础，计算特定温度范围内的钢管冷却速度。以规格为ϕ193.7×13.72 mm的钢管从1 000℃冷却到50℃为例，详解计算过程.

沿钢管厚度方向设置7个节点，每个节点之间的距离相等，节点1在钢管的外表面，节点7在钢管内表面，如图2所示，可将式（11）变换为式（13）。

图2 空间节点划分示意图Fig.2 Schematic of the node partition

节点2～7稳定的条件为

钢管材质：普通碳素钢，钢管的密度ρ＝7 840 kg／m3，水温θf：20℃，钢管的导热系数取λ＝32 W／（m·℃）。在现场超快冷设备水量为1 500 m3／h，水压为0.5 MPa，传送辊道速度为0.8 m／s的工况下，修正计算得射流冲击的综合换热系数为12 000 W／（m·℃）。

前文所述，根据相变规律将0～1 000℃分成3段计算，分别为：［0，675℃］，［675℃，875℃］，［875℃，1200℃］。

以钢管内表面的温度为标准，选取不同温度范围内的比热容值。根据相关文献中实测的比热容随温度变化的函数［15］，求得每段内比热容的平均值为：［0，675℃］：c＝610 J／（kg·℃）。［675℃，875℃］：c＝970 J／（kg·℃）。［875℃，1200℃］：c＝650 J／（kg·℃）。由H＝13.72 mm可得步长h＝H／6＝2.286 67 mm。

综合考虑，选取时间步长Δt为0.01 s，之后建立具体的差分方程，进行迭代计算。

2.2 计算结果

r＝0.012 009，2r＝0.024 018，1-2r＝0.975 982，B＝0.857 501，2rBθf＝0.411 909，1-2r-2rB＝0.955 386。

于是可得在此区间的迭代差分方程组矩阵：

由初始温度开始，进行迭代计算，直到θ7＜874时，更换比热容的数值，继续用相同的方法计算。计算结果为规格是ϕ193.7×13.72 mm的钢管冷却过程的温度—时间曲线，如图3所示。同理可得其他规格钢管的温度-时间曲线。

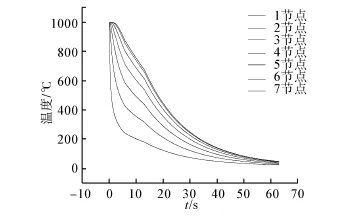
图3 ϕ193.7×13.72 mm规格钢管1～7节点的温度-时间曲线Fig.3 1～7 node temperature⁃time curve of ϕ193.7× 13.72 mm pipe specifications

2.3 现场测试验证

利用现场钢管超快冷设备中的实际温降曲线来验证数学模型的计算精度。在上述工况条件下，选取1、4、7节点进行验证。将热电偶分别插入ϕ193.7× 13.72 mm钢管内壁和1／2壁厚处，测量钢管通过超快冷设备时钢管内壁和1／2壁厚处的温度变化情况，利用红外测温仪测量钢管外壁的温降。将钢管外壁、1／2壁厚处以及内壁的实测温降曲线与图3中的1、4、7节点曲线进行对比，如图4所示。由图可知计算温降曲线与实际温降曲线基本相同，模型计算精度较高。

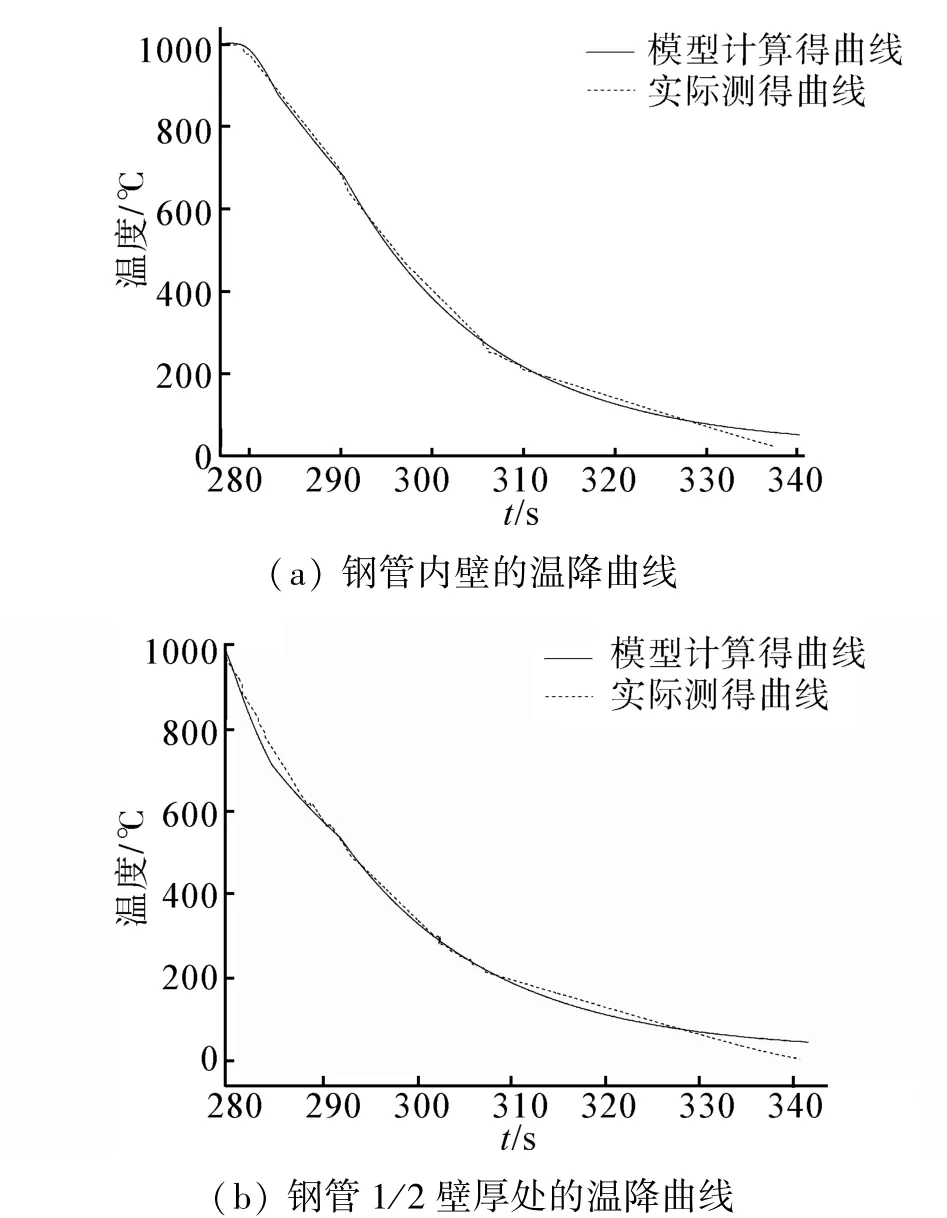
图4 钢管实际温降曲线与模型计算曲线的对比图Fig.4 Comparison of steel pipe actual temperature drop curve and calculated curve

3 结论

本文结合东北大学轧制技术及连轧自动化国家重点实验室自主研发的钢管超快冷设备，深入研究射流冲击水冷的换热机理，建立钢管超快冷过程数学模型，经现场试验验证，该数学模型与计算方法的精准度很高，具有可应用性和执行性.

利用此温降数学模型可以较精确地计算出钢管超快冷过程的温度变化，将其嵌入钢管超快冷自动控制系统，能够完成温度控制的预计算，工艺参数预调整、典型钢种的组织预测等功能。本文研究的数学模型为钢管超快冷设备实现自动化控制、高精度生产、智能化操作等打下了坚实的基础，填补国内在该领域的空白。

［1］王国栋.新一代控制轧制和控制冷却技术与创新的热轧过程［J］.东北大学学报：自然科学版，2009，30（7）：918⁃919.

WANG Guodong.New generation TMCP and innovative hot rolling process［J］.Journal of Northeastern University：Natu⁃ral Science，2009，30（7）：918⁃919.

［2］王昭东，袁国，王国栋，等.热带钢超快速冷却条件下对流换热系数研究［J］.钢铁，2006，41（7）：54⁃64.

WANG Zhaodong，YUAN Guo，WANG Guodong，et al.Heat transfer coefficient of hot rolled strip during ultra fast cooliing process［J］.Iron＆Steel，2006，41（7）：54⁃64.

［3］PUSSEGODA L N，YUE S，JONAS J J.Effect of intermedi⁃ate cooling on grain refinement and precipitation during roll⁃ing of seamless tubes［J］.Material Science and Technology，1991，7（2）：129⁃130.

［4］PUSSEGODA L N，YUE S，JONAS J J.Laboratory simula⁃tion of seamless tube piercing and rolling using dynamic re⁃crystallisation schedules［J］.Metallurgical Transactions A，1990，21A（1）：153⁃154.

［5］付天亮.中厚板辊式淬火机冷却过程数学模型的研究及控制系统的建立［D］.沈阳：东北大学，2010：17⁃61.

FU Tianliang.Research of medium plate roller quenching machine cooling process mathematical model and establish⁃ment of control system［D］.Shenyang：Northeastern Univer⁃sity，2010：17⁃61.

［6］赵宪明，孙艳坤，王永红.轴承钢棒材超快速冷却的试验研究［J］.东北大学学报：自然科学版，2010，31（7）：947⁃952.

ZHAO Xianming，SUN Yankun，WANG Yonghong.Comm⁃ericial test of ultra⁃fast cooling for bearing steel bar［J］.Journal of Northeastern University：Natural Science，2010，31（7）：947⁃952.

［7］赵宪明，郭飞，王丽娜，等.超快冷对H型钢冷却变形的影响［J］.东北大学学报：自然科学版，2012，33（7）：949⁃952.

ZHAO Xianming，GUO Fei，WANG Lina，et al.Effect of ultra⁃fast cooling on cooling distortion for H⁃beam steel［J］.Journal of Northeastern University：Natural Science，2012，33（7）：949⁃952.

［8］WANG Xuefeng，ZHANG Nengli.Numerical analysis of heat transfers in pulsating turbulent flow in a pipe［J］.Interna⁃tional Journal of Heat and Mass Transfer，2005，48：3957⁃3970.

［9］韩会全，陈泽军，胡建平，等.J55钢级焊接油井管在线空冷工艺的研究［J］.钢管，2012，41（3）：24⁃27.

HAN Huiquan，CHEN Zejun，HU Jianping，et al.Study on on⁃line controlled⁃cooling process for j55 oil well weld pipe［J］.Steel Pipe，2012，41（3）：24⁃27.

［10］许亚华.日本无缝钢管水淬工艺［J］.钢管，1996（3）：57⁃61.

XUN Yahua.Water⁃quenching technoligies for seamless steel pipes employed in Japan［J］.Steel Pipe，1996，（3）：57⁃61.

［11］李彬，郭东，钱强，等.钢管内喷旋流淬火技术［J］.金属热处理，2008，33（7）：77⁃79.

LI Bin，GUO Dong，QIAN Qiang，et al.Internal rotation quenching technology for steel pipe［J］.Heat Treatment of Metals，2008，33（7）：77⁃79.

［12］张少军，胡树山，刘国勇，等.基于Fluent的无缝钢管控制冷却喷嘴布置参数［J］.北京科技大学学报，2010，32（1）：123⁃127.

ZHANG Shaojun，HU Shushan，LIU Guoyong，et al.Lay⁃out parameters of controlled cooling nozzles for seamless pipes based on fluent software［J］.Journal of University of Science and Technology Beijing，2010，32（1）：123⁃127.

［13］骆宗安，王国栋，冯莹莹，等.一种钢管超快速淬火冷却装置［P］.中国，ZL 201210345413.4，2013⁃09⁃25.

［14］小門纯一.熱間压延における材料の温度変化の予想计算法に關する基礎的研究［J］.塑性と加工，1970，11：816⁃818.

［15］TAN X，CONWAY P P.Thermo⁃mechanical properties and regression models of alloys：AISI 305，CK 60，CuBe2 and Laiton MS 63［J］.Materials Processing Technology，2005，168：152⁃16.

Development of mathematical model for ultra⁃fast cooling process of a steel pipe

FENG Yingying1，LUO Zong'an1，WANG Lipeng1，HUI Nanmu2
（1.The State Key Laboratory of Rolling Technology and Automation，Northeastern University，Shenyang 110819，China；2.School of Information Science and Engineering，Northeastern University，Shenyang 110819，China）

In order to improve the temperature control precision，cooling uniformity and the control accuracy of mi⁃crostructure and performance during ultra⁃fast cooling process of a steel pipe，the heat transfer mechanism of cooling process was analyzed for determining that jet impingement was the main heat transfer way of steel pipe ultra⁃fast cooling process.The heat transfer coefficient of the pipe surface was measured using the inverse heat conduction method.The jet impingement heat transfer mathematical model of ultra⁃fast cooling process was built using heat con⁃duction equation，and it is solved by the third boundary condition and finite difference method.Utilizing this mathe⁃matical model，the average cooling rate and the spent time within a specific temperature range can be calculated；the temperature drop and the average cooling rate within a certain time can also be calculated.After field tests，the temperature drop curve calculated by this mathematical model is basically the same as the actual temperature drop curve，verifying that the mathematical model has high accuracy，and its practical.

steel pipe；ultra⁃fast cooling；jet impingement heat transfer；mathematical model

10.3969／j.issn.1006⁃7043.201310065

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006⁃7043.201310065.html

TF31，TG335.71

A

1006⁃7043（2015）02⁃0252⁃05

2013⁃10⁃24.网络出版时间：2013⁃11⁃27.

国家自然科学基金资助项目（51001023）；中央高校基本科研业务费资助项目（N120307002）.

冯莹莹（1982⁃），女，助理研究员，博士.

冯莹莹，E⁃mail：fengyy＠ral.neu.edu.cn.