齿轮曲柄滑块机构传动副间隙对传动精度的影响研究①

余良栋 王 胜 韩建友 李 威

(1:宝山钢铁股份有限公司钢管条钢事业部 上海201900; 2:北京科技大学机械工程学院 北京100083)

·设计与研究·

齿轮曲柄滑块机构传动副间隙对传动精度的影响研究①

余良栋②1王 胜2韩建友2李 威2

(1:宝山钢铁股份有限公司钢管条钢事业部 上海201900; 2:北京科技大学机械工程学院 北京100083)

以某轧机径向调整用曲柄滑块机构为对象，研究该调整机构中传动副机械间隙对轧辊辊缝波动的影响情况。研究过程中首先利用矢量法建立曲柄滑块机构滑块运动和轧辊中心距之间的函数关系，然后把径向调整机构中因为安装误差、磨损产生的间隙转化为曲柄滑块机构中相应杆长的变化，最后找出机械间隙与轧机辊缝波动的关系，并得出一些有用结论。

间隙分析 曲柄滑块机构 辊缝波动

曲柄滑块机构是机械传动中的常用机构，该机构中的传动副主要由转动副和移动副构成[1]。传动过程中，各传动副由于磨损等原因会产生机械间隙，这些间隙会对机构运动精度产生影响[2-3]。某轧机辊缝径向调整机构主要由曲柄滑块机构和齿轮副组成，该调整机构传动副中机械间隙的存在对轧机的轧制精度影响很大[4]。即以齿轮曲柄滑块机构为研究对象，对该轧机径向调整机构间隙和轧辊辊缝波动之间的关系进行分析研究。

1 齿轮曲柄滑块机构工作原理

齿轮曲柄滑块传动机构如图1所示。该机构中有两个固定铰链C、F；一个齿轮与曲柄BC固连，以转动副C为旋转轴，另一个齿轮通过转动副F与地面连接，两齿轮中心距保持不变；两轧辊分别与两齿轮固连，轧辊中心D1、D2与齿轮中心C、F具有一定的偏心量；滑块是一个带耳轴的螺母，通过丝杠驱动实现水平直线运动。该机构具体调整方法如下：

丝杠转动→滑块水平移动→连杆平面运动→曲柄转动→齿轮副啮合运动→轧辊随齿轮转动而转动。由于齿轮和轧辊轴线存在偏心量，所以轧辊在随齿轮转动时就会使得两轧辊中心距发生变化，从而实现轧辊中心距的调整。

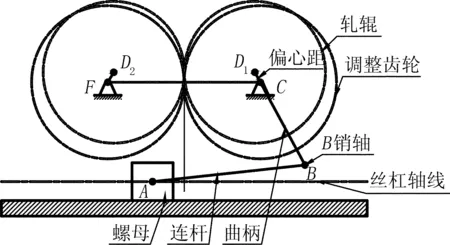
图1 曲柄滑块齿轮机构

在利用曲柄滑块齿轮机构对轧辊中心距进行反复调整过程中，各传动副不可避免的会产生磨损，这种磨损使得相连接构件之间产生机械间隙，而机械间隙的存在会使得轧机在进行轧制时轧辊产生波动，从而影响轧制精度。因此分析机械间隙和轧辊辊缝波动之间的关系就显得尤为重要。该传动机构中存在间隙的部位主要有以下几个方面：丝杠与螺母轴向间隙、丝杠与螺母径向间隙、螺母耳轴与连杆转动副间隙、曲柄连杆与连接销转动副间隙、齿轮传动时齿侧间隙。分析这些机械间隙与轧辊波动之间的关系从而找出主要间隙，实际操作中采取相应措施以减小间隙对辊缝波动的影响。

在下面几节中将采用数学方法完成齿轮曲柄滑块机构从建模到间隙分析的过程。

2 齿轮曲柄滑块调整机构间隙与辊缝波动关系的建模

为了分析齿轮曲柄滑块机构机械间隙和辊缝波动之间关系，需要建立两者之间的方程，然后对这个方程进行分析从而得出一些结论。

2.1 无间隙数学建模

对齿轮曲柄滑块传动机构进行分析首先建立无机械间隙时的数学模型，然后将各位置机械间隙在该数学模型中进行适当表达，从而建立有机械间隙时各机构间隙和辊缝波动之间的关系。所建立的数学模型为中心距处于任意位置的通式，通过调整得到轧辊中心距为一些特殊位置时的情况，从而分析相关规律。

以滑块移动的轴线为X轴，以过F点的竖直线为Y轴建立坐标系，如图2所示。

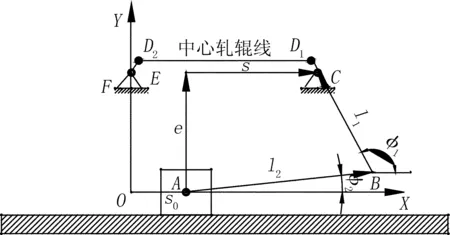
图2 数学模型表达图

图2中相应的参数关系如下：

s0为螺母销A在坐标系中的横坐标，s0Ⅰ=-43.89mm；s0Ⅱ=-1.63mm，s0Ⅲ=41.86mm；AB为连杆长度，杆长l2=155mm；BC为曲柄长度，杆长l1=92mm；AE为螺母上销轴轴线与齿轮轴线的垂直距离，用e表示；EC为螺母上销A轴线与点C轴线的水平距离，用s表示,s=CF-s0；CD1、FD2为齿轮与轧辊偏心距，CD1=FD2=7mm；CF为齿轮两轴线距离，CF=150mm；D1D2为轧辊两轴线距离，用d表示；φ1为杆l1与x轴夹角；φ2为杆l2与x轴夹角。

建立AB、BC、AE、EC和D1D2的函数关系。轧辊中心距D1D2为D1、D2两点x坐标的差值，所以若求中心距求出D1、D2两点x坐标即可。按照曲柄滑块机构建立数学方程，求得D1、D2两点x坐标，从而求得上下两轧辊中心距。具体建立方法如下：

在坐标系中建立曲柄滑块机构的矢量图(如图2所示)，用矢量法建立该曲柄滑块机构的方程：

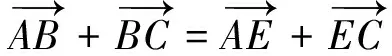
(1)

l2×eiφ2+l1×eiφ1=e×eiπ/2+s×ei×0

(2)

利用欧拉公式将式(2)展开，并令展开式等号左右两边实部和虚部分别相等，得

(3)

方程组(3)两边平方相加消去φ2，得

(4)

令：

(5)

并利用关于φ1半角公式：

(6)

(7)

(8)

分析所得解中的正负号，取正号符合本模型要求。

设实际中心距用d表示，理论中心距用d0表示，中心距为D1、D2两点x坐标的差值

d=xD1-xD2

(9)

xD1=xc+CD1×cosφ1

(10)

(11)

则中心距

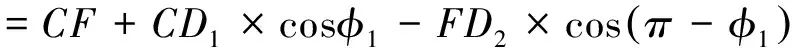
(12)

以上即建立了杆AB、BC、AE、EC与中心距D1D2的关系，亦即d是l1、l2、e、s的函数。

(13)

上述方程为无间隙情况下各构件和中心距之间的数学方程，考虑间隙时可改变其中某些变量进行分析，这在下面进行分析。

2.2 有间隙数学建模

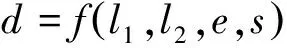
(14)

上式中Δl2、Δe、Δs为各间隙。

在建立无间隙下中心距和构件关系的过程中，没有考虑齿轮副的齿侧间隙，因为齿轮在曲柄滑块机构中没有表示出来。考虑间隙的情况下，齿轮齿侧间隙对中心距产生影响(齿侧间隙的存在使得齿轮发生转动，这个转角直接反映到φ1的变化上，又因为φ1和中心距d有关，所以d是φ1的函数)。因此在分析调整机构间隙对辊缝波动的影响时应该把该间隙项加入。原中心距方程经过修正后变为：

(15)

由于d的函数关系比较复杂，所以求解d对各自变量的导数时采用数值差分的方法计算。差分公式：

(16)

式中h—函数的步长(变量步长)。

根据该公式求得各个变量在初值处的导数：

(17)

(18)

(19)

(20)

将所求得各个导数值代入：

(21)

上述变量与机械间隙对应关系如表1所示。

表1 变量与机械间隙对应表

这一求解微小变化的过程通过编程的方法进行。利用Matlab编写相应的程序，确定各间隙和中心距之间的关系，通过改变间隙量的大小，从而得到不同间隙条件下中心距的大小。

3 齿轮曲柄滑块调整机构对辊缝波动影响的分析

上面一节建立了齿轮曲柄滑块机构机械间隙与轧辊中心距之间的数学关系。当轧辊中心距取不同值(即轧制不同直径的线材)时，通过这一数学关系便可以得出机械间隙对辊缝波动影响程度的大小。

三个位置时的机械间隙与辊缝波动之间关系的对比曲线如下图3、图4、图5所示。

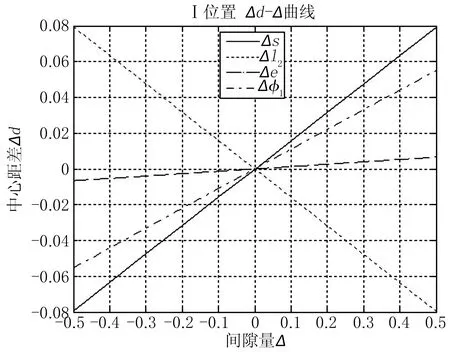
图3 Ⅰ位置时不同机械间隙对比曲线

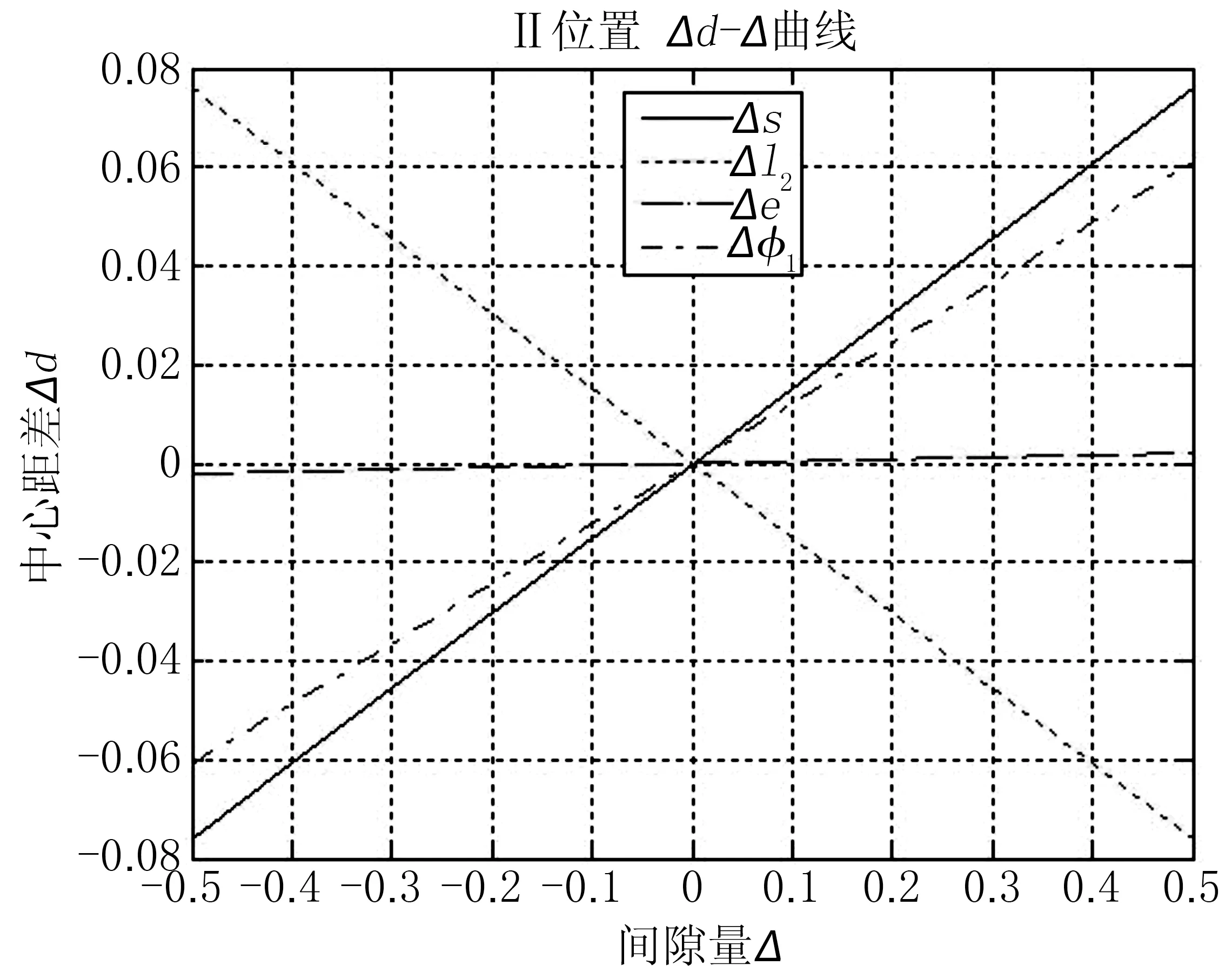
图4 Ⅱ位置时不同机械间隙对比曲线图

图5 Ⅲ位置时不同机械间隙对比曲线

图3、图4、图5中，横坐标表示各机械间隙量的大小，纵坐标表示辊缝波动量的大小，变量与机械间隙的对应关系参照表1所示，曲线表示机械间隙取不同值时辊缝波动量的大小。

通过对上述图线的分析，可以得出以下规律：

1)分别分析图3、图4、图5，可以看出当机械间隙大小相同时，不同机械间隙对辊缝波动影响量的大小不同，这种影响量的大小顺序依次均为：Δφ1>Δl2≈Δs>Δe，即齿轮齿侧间隙>丝杠螺母径向间隙≈丝杠螺母轴向间隙>连杆AB、曲柄BC与销B间隙。

2)对比分析图3、图4、图5，可以看出同一机械间隙在轧辊中心距取不同值时对辊缝波动影响趋势相同，但影响量的大小不同，影响量的大小顺序为：

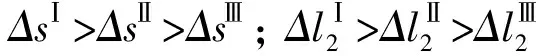
3)分析图3、图4、图5可以看出当轧辊中心距取不同值时，不同机械间隙对辊缝波动量影响大小顺序具有一定的规律性；同一机械间隙对辊缝波动的影响量大小不具有规律性，需要分别考虑。

4)对图中曲线的分析可以看出，当间隙量较小时，机械间隙量和辊缝波动量之间的对应关系可以近似看作线性关系，在实际计算过程中可以计算出相应K值，然后通过线性计算近似计算出相应机械间隙对辊缝波动的影响量大小。

4 结论

通过以上分析可以看出，齿轮曲柄滑块调整机构中各机械间隙会对辊缝波动产生影响，不同位置处间隙对辊缝波动的影响程度不同，同一位置的间隙当轧辊中心距为不同值时对辊缝波动的影响程度也不同。调整机构中齿轮齿侧间隙对辊缝波动的影响程度最大，其次是丝杠与螺母轴向间隙对辊缝波动的影响，螺母销轴与连杆间隙、连杆与销轴间隙、销轴与曲柄间隙对辊缝波动的也有一定程度的影响，丝杠螺母径向间隙对辊缝波动的影响可忽略不计。以上间隙实际轧制过程中要注意检测。通过上面分析中给出的方法可以计算出机械间隙对辊缝波动影响程度的具体数值，同时能够计算出辊缝波动量一定时允许间隙量的大小。机械间隙在定径机径向调整中不可避免，为得到高的轧制精度，在实际轧制过程中要根据上述分析结论定时检测对辊缝波动影响较大位置的机械间隙。

[1]宋亮，赵鹏兵．曲柄滑块机构的运动精度分析与计算[J]．科学技术与工程，2011，Vol.11(10)：2201-2205.

[2]史天录，冯元生．RCCC空间机构的运动精度和可靠性分析[J]．机械科学与技术，1995(1)：47-51.

[3]Dubow sky S.An analytical and experimental study of the prediction of impacts in planar mechanical systems with clearances. ASMEJ.of Mechanisms, Transmissions, and Automations in Design, 1984, 106:444-451.

[4]Soong K.A theoretical and experimental investigation of the dynamic response of a slider-crank mechanism with radial clearance in the gudgeon-pin joint. ASME Journal of Mechanical Design, 1990, 112: 183-189.

[5]同长虹，黄建龙．曲柄滑块机构中滑块输出位移的可靠性分析[J]．上海交通大学学报，2010，Vol.44(12)：1716-1726.

[6]王勤．轧机主传动系统的扭振分析与建模[J]．冶金设备，2009(8)：6-9.

Research on the Relationship Between the Space of Gear and Slider-crank Mechanism and the Transmission Accuracy

Yu Liangdong1Wang Sheng2Han Jianyou2Li Wei2

(1:Steel Bar Department, Baosteel Branch, Shanghai Baosteel Co. Ltd, Shanghai 201900; 2:School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083)

This paper′s research based on the slider-crank mechanism for radial adjustment of a kind of rolling mill. It mainly researched the relationship between mechanical transmission space and the roll gap fluctuation. The function between slider-crank mechanism movement and the roll center distance was firstly founded, which is according to the method of vector. Then the mechanical transmission spaces because of the installation error and abradant of the radial adjustrnent mechanism were transformed into the change of linkage′s length. in the end the relationship between the spaces and the roll gap fluctuation was identified and some conclusion was drawn.

Analysis of gap Slider-crank mechanism Roll gap fluctuations

国家自然科学基金资助项目(51275035)

余良栋，男，1971年出生，1993 年毕业于安徽工业大学冶金机械专业，获学士学位，2007年毕业于浙江大学机电工程专业，获硕士学位，高级工程师

TG333.15

A

10.3969/j.issn.1001-1269.2015.04.002

2015-03-11)